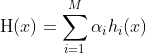集成学习详解
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。
目录
一、集成学习的产生原因与相关定义
1、产生原因
2、相关定义
（1）同质集成
（2）异质集成
二、集成学习的主要问题和思路
1、主要问题
2、思路
三、Boosting
1、工作机制
2、Boosting的两个核心问题
（1）在每一轮如何改变训练数据的权值或概率分布？
（2）通过什么方式来组合弱分类器？
3、代表算法——AdaBoost（Adaptive boosting）
（1）算法步骤
（2）推导过程
四、Bagging与随机森林
1、Bagging
（1）思想
（2）工作机制
2、随机森林
五、学习器结合策略汇总
1、学习器结合的好处
（1）降低误选的假设空间导致泛化性能不佳的风险
（2）降低陷入糟糕局部极小点的风险
（3）扩大假设空间
2、结合策略
（1）平均法
（2）投票法
（3）学习法
六、多样性
1、多样性度量
（1）不合度量
（2）相关系数
（3）Q-统计量
（4）k-统计量
2、多样性增强
（1）数据样本扰动
（2）输入属性扰动
（3）输出表示扰动
（4）算法参数扰动
一、集成学习的产生原因与相关定义
1、产生原因
在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际往往不这么完美与理想，有时我们只能得到多个有偏好的模型（即在某些方面表现的比较好），这样的模型称为弱监督模型。
但是一个过优秀的模型可能会出现过拟合问题，但多个有偏好的模型组合成的模型不容易出现过拟合问题。
集成学习即组合多个弱监督模型以期望得到一个更好更全面的强监督模型。
集成学习潜在的思想是即便某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。
2、相关定义
单个学习器我们称为弱学习器（个体学习器），相对的集成学习则是强学习器。
（1）同质集成
集成中只包含同种类型的个体学习器（例如全是决策树）。
其中的个体学习器被称为“基学习器”。
相应的学习方法称为“基学习算法”。
（2）异质集成
集成中只包含不同类型的个体学习器（比如有决策树，有神经网络等）
其中的个体学习器被称为组件学习器。
二、集成学习的主要问题和思路
集成学习是一种技术框架，其按照不同的思路来组合基础模型来达到更好的目的。
1、主要问题
（1）如何得到若干个个体学习器
（2）如何选择一种结合策略，将这些个体学习器集合成一个强学习器
2、思路
要获得好的集成，个体学习器应“好而不同”，即个体学习器准确性不能过低并且学习器间要有差异的偏向（即对某一类的预测更准确）。
目前的集成学习大致分为2类：
（1）个体学习器间存在强依赖关系，必须串行生成的序列化方法（代表：Boosting）；
（2）个体学习器间不存在强依赖关系，可同时生成的并行化方法（代表：Bagging和随机森林）；
三、Boosting
1、工作机制
先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器（即根据弱学习的学习误差率表现来更新训练样本的权重，使之前弱学习器学习误差率高的训练样本点的权重变高，即让误差率高的样本在后面的弱学习器中得到更多的重视）；如此重复进行，直至基学习器数目达到事先指定的值T，最终再将这T个基学习器进行加权结合。
2、Boosting的两个核心问题
（1）在每一轮如何改变训练数据的权值或概率分布？
通过提高那些在前一轮被弱分类器分错样本的权值，减小前一轮分对样本的权值，来使得分类器对误分的数据有较好的效果。
（2）通过什么方式来组合弱分类器？
通过加法模型将弱分类器进行线性组合（比如AdaBoos算法）；
通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型（比如GBDT算法）；
3、代表算法——AdaBoost（Adaptive boosting）
标准AdaBoost只适用于二分类。
（1）算法步骤
A、初始化训练数据权重相等，训练第一个学习器
即假设每个训练样本在基分类器的学习中作用相同
B、反复学习基本分类器，在第m轮中执行以下步骤（其中：
）：
✨在权值分布为
的训练数据上，确定基分类器；
✨计算该学习器在训练集中的错误率
函数为该学习器代表的函数；
- xt为相应的样本属性；
- yt为对应的样本标签；
若
为0.5则没有投票权重，直接跳过，进行下一轮；
✨计算该学习器的投票权重
这里即体现：
若
若
✨根据投票权重，对训练数据重新赋权
其中：
是一个归一化因子；
是当前训练样本中样本x所占的权重；
是下一次训练样本中样本x所占的权重；
C、对这M个学习器进行加权投票
（2）推导过程
假设分为2类，y为1或-1。
目标式为基学习器的线性组合，即：
为了得到更好的分类器，则我们希望损失函数尽可能的小，即以下最小化指数损失函数：
因此我们对其做H(x)的偏导，得：
令其为0，可得：
又：
；即当y为什么值时P(f(x)=y|x)最大，y的取值为1或-1。
这意味着
达到了贝叶斯最优错误率。
![L(H \mid D)=E(\exp [-f(x) H(x)]),x\in D](http://img.e-com-net.com/image/info8/08eeffe57b4147acae432fa56d73a24a.gif){kind=small}
✨求
所以加入基分类器权重后，
的指数损失函数为：
其中
为基分类器
的错误率；
最小化指数损失函数后可得到（令导数为0）：
；这个就是我们前面所说的这个分类器的投票权重啦。
✨求
在获得
之后样本分布将进行调整，使得下一轮的基学习器 能纠正的一些错误
因为
，所以上式可用
的泰勒展开式近似：
所以理想基学习器就是找到h使得上式最小：
令表示一个分布：
所以
等价于：
又因为：
即当f(x)h(x)不等时为-1，相等时为1。
所以又可以化为：
由上式可以看到是在数据集下得到（残差逼近思想）
✨求
这里对应上面算法过程中的
四、Bagging与随机森林
1、Bagging
（1）思想
即训练多个分类器取平均；
从训练集中进行子抽样组成每个基模型所需要的子训练集（子训练集相互间可有重叠），对所有基模型预测的结果进行综合产生最终的预测结果。
（2）工作机制
-
从原始样本集中抽取训练集。每轮从原始样本集中使用自助采样法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中），共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）；
-
每次使用一个训练集得到一个模型，k个训练集共得到k个模型；
-
对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）。
2、随机森林
详见RF模型（随机森林模型）详解_tt丫的博客-CSDN博客_rf模型
五、学习器结合策略汇总
1、学习器结合的好处
（1）降低误选的假设空间导致泛化性能不佳的风险
从统计方面上看，由于学习任务的假设空间往往很大，可能有多个假设在训练集上达到同等性能，此时如果使用单学习器可能会因为误选而导致泛化性能不佳，结合多个学习器则会减少这一风险。
（2）降低陷入糟糕局部极小点的风险
从计算方面上看，对于一个问题的求解有时可能不止一个局部极小，有的局部极小点所对应的泛化能力很差，而多个学习器结合可以降低陷入糟糕局部极小点的风险。
（3）扩大假设空间
从表示方面上看，某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间内。
多个学习器，相应的假设空间就会扩大，有可能学到更好的近似。
2、结合策略
（1）平均法
对于回归问题最常用的就是平均法。
又分为简单平均法（每个学习器权重相同）和加权平均法。
注意：
加权平均法的权重一般都是从训练数据中学习而得。现实任务中的训练样本通常不充分或存在噪声，这使得学出的权重不完全可靠；尤其对于规模比较大的集成，要学习的权重比较多，较容易导致过拟合。因此，加权平均法未必比简单平均法优秀。
（2）投票法
对于分类问题常用投票法集成。
投票法又分为绝对多数投票法，相对多数投票法和加权投票法。
绝对多数投票法
即若某类得票过半，则预测为该类，否则拒绝预测。
相对多数投票法
预测为得票最多的类，若同时有多个类获得最高票，则从中随机选出一个。
加权投票法
与加权平均法类似。
（3）学习法
当训练数据很多时，可通过另一个学习器来进行结合。
典型代表是Stacking（思想：堆叠不同的分类器）
✨概念引入
A、初级学习器：个体学习器
B、次级学习器（元学习器）：用于结合的学习器
✨stacking具体算法：
①以原始训练集为输入训练模型得到基模型（也叫 level-0 模型）
基模型可以是多种不同的分类器进行训练；
②以基模型在原始训练集上的预测（类概率）作为输入，以原始测试集上的真实标签作为输出形成新的数据集，然后拿这个训练集训练生成元模型（也叫 level-1 模型）。
在实际使用Stacking方法时，为了避免过拟合的风险，常常伴随着交叉验证操作，这是为了防止过拟合。
六、多样性
1、多样性度量
多样性度量是用于度量集成中个体分类器的多样性。
分类器
和
的预测结果列联表为：
 |
 |
|
 |
a | c |
 |
b | d |
- a为同时预测为+1的个数；
- a+b+c+d = m（样本总数）；
（1）不合度量
即表示两个学习器的分类结果不同的占比。
值越大则多样性越大。
（2）相关系数
值域为 [-1，+1] ；若 和 无关，则值为 0 ；若正相关在，则值为正，否则为负。
其绝对值越小，说明多样性越大。
（3）Q-统计量
注：
，且两者符号相同。
大于0则说明两者更相似，值越小说明多样性越大。
（4）k-统计量
其中，p1是两个分类取得一致的概率；p2是两个分类器偶然达成一致的概率；
若k=1，两个分类器完全一致（即p1为1）；若k=0，两者仅偶然达成一致；
仅在 和 达成一致的概率甚至低于偶然性的情况下取负值。
2、多样性增强
为了在集成学习中有效生成多样性大的个体学习器，一般我们在学习过程中引入随机性，常见做法是进行扰动操作。
（1）数据样本扰动
通常是基于采样法。
Bagging采用自助采样法，AdaBoost采用序列采样法。
数据样本扰动法对“不稳定基学习器”（决策树——容易过拟合，神经网络）很有效。
补：稳定基学习器：线性学习器，SVM，朴素贝叶斯，k近邻学习器等。
（2）输入属性扰动
用不同的属性子集（“子空间”）进行训练。
例如：随机子空间算法
（3）输出表示扰动
基本思路：对输出表示进行操纵以增强多样性。
例如：
翻转法：随机改变一些训练样本的标记；（对训练样本标记做改动的思想）
输出调制法：将分类输出转化为回归输出后构建个体学习器；（对输出表示进行转化的思想）
ECOC法：利用纠错输出码将多分类任务拆解为多个二分类任务来训练基学习器。（将原任务拆分成多个不同的可以同时进行的任务的思路）
（4）算法参数扰动
主要思想是：对学习器中的参数进行随机的不同设置
例如：
负相关法——通过正则化项限制个体神经网络使用不同参数；
将学习过程中的某些环节用其他类似方式替代（对参数较少的算法）；
交叉验证；
欢迎大家在评论区批评指正，谢谢~