论文阅读《Revisiting Domain Generalized Stereo Matching Networks from a Feature Consistency Perspective》

论文地址：https://github.com/jiaw-z/FCStereo
源码地址：https://arxiv.org/pdf/2203.10887.pdf

---

概述

  虽然目前立体匹配网络能取得不错的效果，但在跨域预测时的效果并不佳。在跨域预测过程中，保持匹配像素之间的特征一致性是提高立体匹配网络泛化能力的关键因素。为此，本文提出了像素级的对比学习，使用立体对比特征损失（The stereo contrastive feature loss）约束匹配像素之间学习到的特征之间的一致性。为了更好地保持立体特征的跨域一致性，引入立体选择性白化损失（The stereo selective whitening loss）将立体特征信息与特定视角的风格特征信息解耦(消除域敏感信息 )。将同一场景中两个视点之间的特征一致性泛化性转换未知领域之间的特征一致性泛化性。对合成数据进行训练并将其推广到四个真实的测试集时，该方法在几个最先进的网络上实现了优越的性能。本文的贡献主要如下：

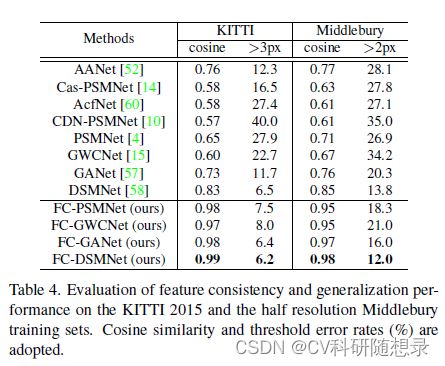
• 观察到目前大多数立体匹配方法的匹配点之间提取到的特征不一致，并证明了提高立体特征一致性可以提高模型的泛化性能。
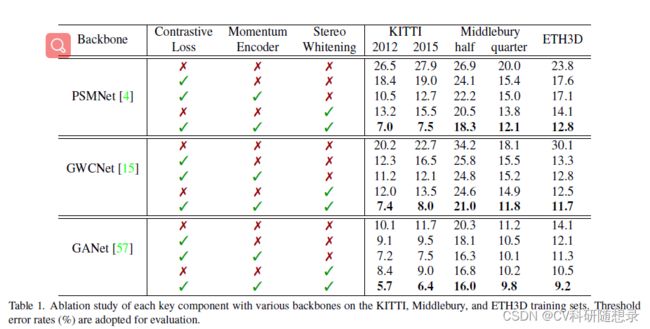
• 提出了两个损失函数（即立体对比特征损失和立体选择性白化损失）来实现立体特征的跨域一致性，且这两个损失可以很方便地嵌入到现有的立体匹配网络中。
• 所提出的方法被应用到几种立体匹配网络架构中，并显示出它们在域泛化性能上的显著提升。

---

模型架构

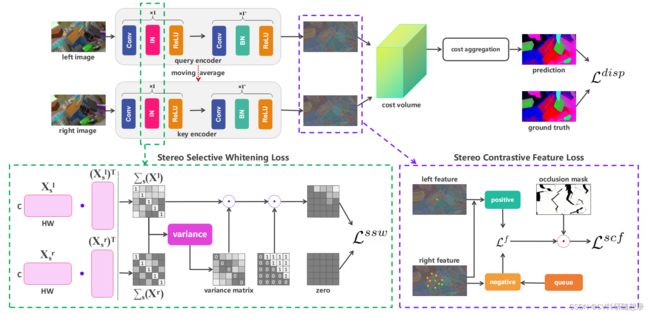
Stereo Contrastive Feature Loss （立体特征对比损失）

  受自监督特征对比学习的启发，本文引入了一种立体特征的对比学习机制，即立体对比特征损失(SCF)，包括立体特征之间像素级的对比损失、使用动态更新的字典队列引入多源的负样本集，进一步提高了特征一致性。

正样本对

  假设左右试图的同名点之间的特征对为正样本对，通过左视图的像素坐标与真值来计算得到右视图对应像素坐标的特征向量，这样得到的左视图的索引向量记为 ${\varphi }_{u,v}^l$ , 对应右视图的特征向量记为 ${\varphi }_{u-d,v}^r$，为此，立体对比特征损失旨在提高正样本对之间的一致性。

负样本对

  对于索引特征 ${\varphi }_{u,v}^l$ ，在右视图中可以找到 $HW-1$ 个负样本可以构成负样本对，若将其全部考虑在内，将会导致模型计算量骤升。为了解决这个问题，文中在局部 $50\times 50$的窗口内随机采样 $N$ 个不匹配的负样本点来与索引点组成 $N$ 个负样本对。

动量编码器

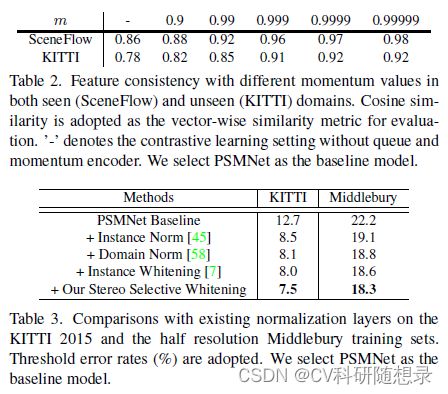
  负样本的选择是表征学习的重要影响因素，从实验中发现只在同一对立体图像之间选择负样本导致最后达不到较高的特征一致性。为此，使用来自其他图像采样而来的点来与参考点构建负样本，并不断将处理过的负样本对更新入字典队列中来加强负样本集的多样性。
  更新一个动态字典队列来存储处理过的负样本，并将权值共享特征提取网络结构改为一个非对称的编码器 (使用权重 $\theta$ 与 $\eta$)。
$${\mathbf{\eta }}_t=m{\mathbf{\eta }}_{t-1}+(1-m){\mathbf{\theta }}_t\text{\hspace{1em}(1)}$$
其中 $t$ 为迭代轮回索引，$m\in [0,1]$ 是动量值。动量值 $m$ 起着核心作用，从实验中得到 $m=0.9999$ 可以得到一个较好的结果。

像素级对比损失

  使用点乘来计算特征对之间的相似性，并使用 infoNCE 来计算像素级别的对比损失如式2所示
$${\mathcal{L}}^f(u,v)=-\log \frac{\exp \left({\varphi }_{u,v}^l\cdot {\varphi }_{u-d,v}^r/\tau \right)}{{\sum }_{{\varphi }^n\in \mathcal{F}(u,v)}\exp \left({\varphi }_{u,v}^l\cdot {\varphi }^n/\tau \right)}\text{\hspace{1em}(2)}$$
其中，$\mathcal{F}(u,v)$ 表示负样本集，包含从 ${\varphi }^r$ 中采样的 $N$ 个负样本和从字典队列中采样的 $K$ 个负样本，$\tau$ 是一个超参数，在本文中，$N=60,K=6000,\tau =0.07$.

非匹配区域滤波

  由于遮挡因素的存在，在遮挡区域利用视差真值计算得到的正样本对存在一定误差，这些不匹配的点对应该被剔除，文中使用左右一致性检查来剔除不匹配点对。本文将重投影误差 $R$ 作为匹配有效性检验的标准，掩码区域 $M$ 表示正确匹配的区域，如式3所示：
$${\mathbf{M}}_{u,v}=\{\begin{array}{ll}1,& {\mathbf{R}}_{u,v}<\delta \\ 0,& \text{ otherwise }\end{array}\text{\hspace{1em}(3)}$$
其中阈值 $\delta =3$ ，使用 $M$ 对 SCF 损失在像素空间进行加权(滤波)：
$${\mathcal{L}}^{scf}=\frac{1}{{\sum }_{(u,v)\in \mathcal{C}}{\mathbf{M}}_{u,v}}\sum _{(u,v)\in \mathcal{C}}{L}^f(u,v)\odot {\mathbf{M}}_{u,v}\text{\hspace{1em}(4)}$$

Stereo Selective Whitening Loss （立体选择白化损失）

  利用对比损失，模型可以在训练集上提取到一致的特征表示。然而，因为域偏差导致的跨域特征一致性的下降是模型泛化性能的下降的主要原因，为此本文提出一种立体选择白化损失(SSW)来解决这个问题。立体匹配网络重常用批归一化（BN）来对特征进行正则化，在训练阶段，BN利用小批量统计量对特征进行正则化，并在推理时使用训练集的总体统计量，使得网络的统计量依赖于训练集，此操作对域变化非常敏感。为了将特征一致性推广到不同域，将一些的BN层改为实例归一化(IN)层，该层分别对每个样本进行归一化，因此与训练集统计无关。对于每个 sample $\mathbf{X}\in {\mathbb{R}}^{C\times HW}$ 有
$${\hat{\mathbf{X}}}_i=\frac{1}{{\sigma }_i}\left({\mathbf{X}}_i-{\mu }_i\right)\text{\hspace{1em}(5)}$$
其中 ${\mu }_i$ 和 ${\sigma }_i$ 是 $\hat{\mathbf{X}}$ 沿着特征通道 $i$ 的均值与方差。进一步考虑在特征协方差中的信息，这是实例归一化所没有处理的，SSW通过抑制视角变化敏感的特征协方差分量来得到特征的一致性表示，也就是去除特征与特征之间的冗余性，首先计算特征向量的方差矩阵 $\Sigma (\hat{\mathbf{X}})$：
$$\Sigma (\hat{\mathbf{X}})=\frac{1}{HW}(\hat{\mathbf{X}})(\hat{\mathbf{X}}{)}^{\mathrm{T}}\text{\hspace{1em}(6)}$$
然后计算 $\sum ({\hat{\mathbf{X}}}^l)\in {\mathbb{R}}^{\mathbb{C}\times \mathbb{C}}$ 与 $\sum ({\hat{\mathbf{X}}}^r)\in {\mathbb{R}}^{\mathbb{C}\times \mathbb{C}}$ 之间的方差矩阵，其中 $n$ 代表第 $n$ 个样本：
$$\begin{array}{rl}{\mu }_{{\Sigma }_n}& =\frac{1}{2}\left({\mathbf{\Sigma }}_n\left({\hat{\mathbf{X}}}^l\right)+{\mathbf{\Sigma }}_n\left({\hat{\mathbf{X}}}^r\right)\right)\\ \mathbf{V}& =\frac{1}{2N}\sum _{n=1}^N\left({\left({\mathbf{\Sigma }}_n\left({\hat{\mathbf{X}}}^l\right)-{\mu }_{{\mathbf{\Sigma }}_n}\right)}^2+{\left({\mathbf{\Sigma }}_n\left({\hat{\mathbf{X}}}^r\right)-{\mu }_{{\mathbf{\Sigma }}_n}\right)}^2\right)\end{array}\text{\hspace{1em}(7)}$$
方差矩阵中的元素 ${\mathbf{V}}_{i,j}$ 表示第 $i$ 通道和第 $j$ 通道之间的对视点变化的敏感性，左右特征间方差较大的协方差元素被认为是对视点变化较敏感的分量，两个特征的关联性较大，在白化损失中应考虑这些协方差元素。所有协方差元素按方差大小分为3组，选择方差值最高的组 $G_p$ 计算掩码 ${\tilde{\mathbf{M}}}_{i,j}$
$${\tilde{\mathbf{M}}}_{i,j}=\{\begin{array}{ll}1,& {\mathbf{V}}_{i,j}\in {\mathcal{G}}_p\\ 0,& \text{ otherwise }\end{array}\text{\hspace{1em}(8)}$$
在左视图的正则化特征上计算SSW损失:
$${\mathcal{L}}^{ssw}=\frac{1}{\Gamma }\sum _{\gamma =1}^{\Gamma }{\Vert {\Sigma }_{\gamma }\left({\hat{\mathbf{X}}}^l\right)\odot \tilde{\mathbf{M}}\odot \hat{\mathbf{M}}\Vert }_1\text{\hspace{1em}(9)}$$
其中协方差矩阵是对称矩阵，因此$\tilde{\mathbf{M}}$ 是一个上三角矩阵，$\Gamma$ 是SSW损失计算的层数，$\gamma$ 是对应的中间层如 ( PSMNet 中的 conv1, conv_2x层)。通过SSW的损失，立体匹配网络学会减少对无关信息的依赖来形成其特征表示。图像对内部的差异大多局限于特定的物理特征，如光的漫反射，这使得模型从有限的训练数据中学习到一些泛化性较强的知识。

---

损失函数

  最终的训练损失是视差损失和上述损失的加权和:
$$\mathcal{L}={\mathcal{L}}^{\text{disp }}+{\lambda }^{scf}{\mathcal{L}}^{scf}+{\lambda }^{ssw}{\mathcal{L}}^{ssw}\text{\hspace{1em}(10)}$$
其中 ${\mathcal{L}}^{\text{disp }}$ 是平滑 $L_1$ 损失。${\lambda }^{scf}$ 与 ${\lambda }^{ssw}$ 为权重因子。 在反向传播过程中，除了右视图特征提取器被实现为左视图特征提取器的移动平均之外，其他所有模块都使用梯度下降方法更新。

---

实验结果

消融实验