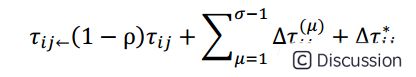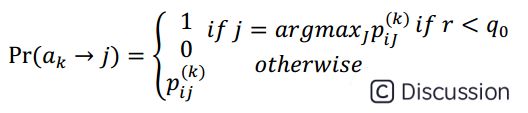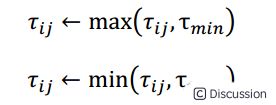【路径规划】基于蚁群算法实现无人机路径规划matlab源码
5.1 介绍
蚁群优化(ACO)是群体智能的一部分，它模仿蚂蚁的合作行为来解决复杂的组合优化问题。它的概念是由Marco Dorigo[1]和他的同事提出的，当他们观察到这些生物在寻找食物时所采用的相互交流和自我组织的合作方式时，他们感到很惊讶。他们提出了执行这些策略的想法，为不同领域的复杂优化问题提供了解决方案，并获得了广泛的欢迎[1, 2]。
蚁群算法是一组被称为人工蚂蚁的软件代理，它们为特定的优化问题寻找好的解决方案。蚁群算法是通过将问题映射成一个加权图来实现的，在加权图中，蚂蚁沿着边缘移动，寻找最佳路径。
蚁群研究(实际上是真正的蚂蚁)始于1959年，当时皮埃尔•保罗•格拉斯(Pierre Paul Grasse)发明了“协同”理论，解释了白蚁的筑巢行为。之后于1983年Deneubourg和他的同事们[3]对蚂蚁的集体行为进行了研究。1988年，Mayson和Manderick发表了一篇关于蚂蚁的自组织行为的文章。最终在1989年，Goss, Aron, Deneubour, and Pasteelson在其研究工作(阿根廷蚂蚁的集体行为)中提出了蚁群算法的基本思想[4]，同年，Ebling及其同事提出了一食物定位模型。1992年，Marco Dorigo(Dorigo, 1992)在其博士论文中提出了蚂蚁系统(Ant System)[1]。一些研究人员将这些算法扩展到各个研究领域的应用中，Appleby和英国电信主管发表了第一个在电信网络中的应用，后来Schoonderwoerd和他的同事在1997年对其进行了改进。在2002年，它被应用于贝叶斯网络中的调度问题。
蚁群算法的设计是基于蚂蚁搜索巢穴和食物位置之间短路径的能力，这可能会因蚂蚁的种类而有所不同。近年来，研究人员对蚁群算法的应用结果进行了研究，结果表明，所使用的大多数人工蚂蚁并不能提供最好的解决方案，而精英蚁群通过重复的交换技术提供了最好的解决方案。他们进一步指出，如果考虑相同的参数，混合和交换方法的性能优于蚁群系统(ACS)。
基于这一理论，研究人员提出了一种专门的蚁群优化方法，可以模拟特定种类的蚂蚁，如黑蚁(Lasius niger或Irodomyrex humilis)，著名的阿根廷蚂蚁。
5.2 人工蚂蚁的概念
自然生物的合作行为常常被证明是解决现实生活中各种复杂问题的一个很好的方法。生物的协作行为吸引了研究人员将它们的智能融入人工智能中，共同努力解决不同领域的各种复杂问题。
5.2.1 真实蚂蚁如何工作
像蚂蚁这样的微小自然生物可以共同工作来完成复杂的任务。这种群居行为是基于蚂蚁在运动时分泌的一种特殊化学物质——信息素。这些信息素吸引其他蚂蚁通过相同的路径，这就证明了为什么蚂蚁总是在群体中交流，蚁丘是如何形成的，以及它们如何能够通过相互交流策略实现复杂的结构。
信息素在蚂蚁之间完成各种集体任务的信息交换中发挥着重要的作用；对我们来说，理解信息素的工作原理以及它们如何帮助蚂蚁找到食物源的最短路径变得非常重要。
5.2.2 蚂蚁如何优化食物搜索
食物搜索过程大致可以分为三个阶段。蚂蚁开始寻找目标时，会在朝随机的方向搜索食物。这些蚂蚁以混乱的方式四处游走，最终当疲惫不堪时就返回巢穴进食和休息。然而，当它们漫步时，如果其中一只遇到了食物来源，它会带着一小块食物回到巢穴，并留下信息素轨迹，这种信息素可以作为其他蚂蚁是否有食物的指示。因此，蚂蚁会沿着信息素轨迹，留下更多的信息素。然而，考虑到蚂蚁可以选择多种路径到达食物源，蚂蚁的初始移动在本质上是有些混乱的，有许多路径连接着巢穴和食物，蚂蚁通常选择信息素更强的路径。信息素随着时间的推移而蒸发，从而到达食物源最短的路径具有最强的信息素；蚂蚁慢慢地向这条路线靠拢，使之成为最优路线，后来形成了蚁群(Fogel等，1966)。
5.2.3 什么是人工蚂蚁
人工蚂蚁不过是一种模拟代理，它模仿真实蚂蚁的一些行为特征，以解决复杂的现实问题。根据计算机科学，它们代表了来自真实蚂蚁行为的多智能体技术。这个概念是建立在这样一个理念之上的：智能可以是许多微小物体的集体努力。这种智能个体的环境网络目前是未来技术的愿景，有望超越目前基于人脑的集中式系统[5]。
人工蚂蚁有着双重特性，一方面，它们是真实蚂蚁行为特征的一种抽象，将蚂蚁觅食行为中最关键的部分赋予人工蚂蚁；另一方面，人工蚂蚁是为了解决实际的工程优化问题，所以人工蚂蚁也具备了一些真实蚂蚁所不具备的本领以增强算法的优化效果。
5.2.3.1 相同
- 相互合作的个体：每个人工蚂蚁都是一个可行解，高质量的解是整个蚁群合作的结果；
- 共同的任务：寻找起点(蚁穴)到终点(食物源)之间的最短路径(最小代价)；
- 信息素-间接通讯：人工蚁群算法中信息素轨迹是通过状态变量来比表示。状态变量用一个nxn维信息素矩阵来表示，其中n表示问题的规模，矩阵中的元素rij表示在节点i选择节点j作为移动方向的期望值。初始化矩阵中每一个元素(如0)，随着蚂蚁在所经过的路径上释放信息素的增多，矩阵中的对应元素也随之改变，人工蚁群算法就是通过修改矩阵中的元素的数值，来模拟自然界中信息素轨迹的更新过程。
- 正反馈：当一些路径上通过的蚂蚁越来越多，其留下的信息素轨迹也越来越多，使得信息素的强度增大。根据蚂蚁倾向于选择信息素强度大的路径的特点，后来的蚂蚁选择该路径的概率也越高，从而增加了该路径的信息素强度，这种选择过程被称为自催化过程。自催化过程利用信息作为反馈，通过对系统演化过程中较优解的自增强作用，使得问题的解向着全局最优的方向不断进化，最终能够有效获得相对较优的解。正反馈在基于群体的优化算法中是一个强有力的机制。
- 信息素的挥发：挥发机制可以使蚂蚁逐渐忘记过去，不受过去经验的过分约束，有利于指引蚂蚁向着新的方向进行搜索，避免早熟收敛。
- 不预测未来状态概率的状态转移策略：只充分利用局部信息，并没有利用前瞻性预测未来的状态。
5.2.3.2 不同
- 人工蚂蚁生活在离散的世界中，它们的移动实质上是由一个离散状态到另一个离散状态的跃迁；
- 人工蚂蚁内部有一个内部的状态，这个私有的状态记忆了蚂蚁过去的行为；
- 人工蚂蚁释放一定量的信息素，它是蚂蚁所建立的问题解决方案优劣程度的函数；
- 人工蚂蚁释放信息素的时间可以视情况而定，而真实蚂蚁是在移动的同时释放信息素，人工蚂蚁可以在建立了一个可行的解决方案后再进行信息素的更新；
5.3 蚂蚁系统
蚂蚁系统是提出的第一个ACO算法[6]，可以以旅行商问题为例说明该算法。在ACO仿真中，每只蚂蚁都要从一个城市到另一个城市，在蚂蚁完成它们的旅程后，蚁群算法会在它们的路径上储存信息素。信息素不仅沉积，而且蒸发。一只蚂蚁从现在的城市到另一个城市旅行的概率与城市间信息素的数量成正比。蚂蚁也被认为对问题有一定的了解，可以帮助它们在旅途中做出决定。它们知道从现在的城市到其他城市的距离，更有可能去一个近的城市而不是一个遥远的城市，因为算法的目标是找到最短路径。蚂蚁系统算法如下所示。
从算法中可以看出每只蚂蚁从城市i去到城市j的概率与这些城市之间路径上信息素的数量成正比，与这些城市之间的距离成反比。比率α/β确定信息素信息相对于距离信息在决定去哪个城市旅行时的重要性。当一只蚂蚁从一个城市i移动到另一个城市j时，这条路径上的信息素的数量与蚂蚁解的质量成正比(也就是说，与蚂蚁的总旅行距离成反比)。
5.4 三种模型
5.4.1 蚁密系统模型
该模型中，一只蚂蚁经过路径(i，j)上释放的信息素量为常数Q，即\ 
5.4.2 蚁量系统模型
该模型中，一只蚂蚁经过路径(i，j)上释放的信息素量为常数Q/dij，即\ 
\ 可以看出，在蚁量模型中，信息素轨迹强度的增加与dij成反比，因此段路径对蚂蚁更有吸引力。
5.4.3 蚁周系统模型
该模型与前两种模型的区别在于蚂蚁k完成一次循环后才会更新信息素，其更新公式如下：
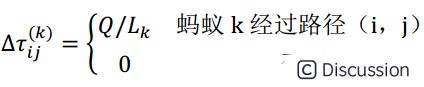\ 在蚁密模型和蚁量模型中，蚂蚁在建立方案的同时释放信息素，利用的是局部信息，而蚁周模型是在蚂蚁已经建立了完整的轨迹后再释放信息素，利用的是整体信息。
5.5 改进的蚁群优化算法
5.5.1 带精英策略的蚂蚁系统
带精英策略的蚂蚁系统(Ant System with elitist strategy，ASelite)，为了使当前的最优解在下一循环中对蚂蚁更有吸引力，在每次循环后给予最优解以额外的信息素，这个最优解就是全局最优解，找到该解的蚂蚁为精英蚂蚁，信息素更新公式如下：
\ 
\ 
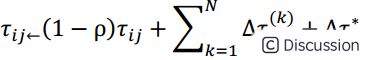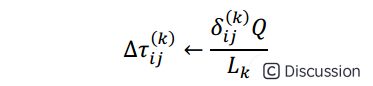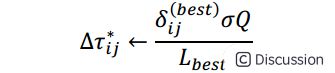\ δij(k)表示第k个蚂蚁经过ij，σ是精英解的个数。
5.5.2 基于优化排序的蚂蚁系统
和蚂蚁系统一样，带精英策略的蚂蚁系统有一个缺点：若在进化过程中，解的总质量提高了，解元素之间的差异减少了，导致选择概率的差异随之减小，使得搜索过程不会集中在到目前为止所找出的最优解附近，从而阻止了对更优解的进一步搜索。当路径长度变得非常接近，特别是当很多蚂蚁沿着局部极优的路径行进时，则对短路径的增强作用被削弱了。
受遗传算法中采用排序选择机制解决选择压力的启发，将排序的概念应用到蚂蚁系统中，就有了基于优先排序的蚂蚁系统(Rank-Bsed Version of Ant System，ASrank)。具体过程如下：当每只蚂蚁都生成一条路径后，蚂蚁按照路径长度排序(L1≤L2≤┈≤Lm)，蚂蚁对信息素轨迹更新的贡献根据该蚂蚁的排名µ的位次进行加权。此外只考虑w只最好的蚂蚁，σ为目前为止所找出的最优路径上轨迹贡献的权值，前σ-1只蚂蚁中的各只所经历的边获得一定量的信息素，其正比于该蚂蚁的排名位次。此外，到目前为止找出最优路径的蚂蚁所经过的边也将获得额外的信息素(这相当于带有精英策略的蚂蚁系统中精英蚂蚁的更新)，所以有如下的更新：
是σ-1只蚂蚁根据排名对信息素轨迹的更新：
5.5.3 蚁群系统
蚁群系统(Ant Colony System，ACS)[7]是由Dorigo和Gambardella在1996年提出的，用于改善蚂蚁系统的性能。蚁群系统在蚂蚁系统的基础上主要做了三个方面的改进：\ (1)状态转移规则为更好更合理地利用新路径和利用关于问题的先验知识提供了方法。
蚁群系统使用双重决策：既可以利用关于问题的先验知识和以信息素形式存储的已经获得信息，又可以进行有向性的探索。通过调节参数q0，可以调节探索新路径的程度和是否使蚂蚁的搜索活动集中于最优解的空间邻域内。
(2)全局更新规则只应用于最优的蚂蚁路径上
在蚁群系统中，每次循环后只对最优蚂蚁经历的路径进行信息素的增强，其他路径由于挥发机制信息素会逐渐减少，这就增大了最优路径和最差路径在信息素上的差异，使得蚂蚁更倾向于选择最优路径中的边，从而使得其搜索行为能够很快地集中造最优路径附近，提高了算法的搜索效率。
(3)建立问题解决方案的过程中，应用局部信息素更新规则
蚂蚁在构造路径的同时进行局部更新，类似于蚁密和蚁量模型中的局部更新，而在每次循环后再对路径进行一次全局的更新。
5.5.3.1 蚁群系统状态转移规则
蚁群系统在构造候选解时使用了伪随机比例规则，位于节点i的蚂蚁通过下式确定选择下一个城市j的概率：
\ r为[0,1]内均匀分布的随机数。
5.5.3.2 蚁群系统全局更新规则
在蚁群系统中，只有全局最优的蚂蚁才被允许释放信息素，这种选择以及伪随机比例规则，其目的都是为了使搜素过程更具有指导性：蚂蚁的搜索主要集中在当前循环为止所找出的最好路径的邻域内。全局更新如下：\ 
5.5.3.3 蚁群系统局部更新规则
\ 由实验发现，设置τ_0=(nL_nn )^(-1)可以产生好的结果，其中n是城市的数量，Lnn是由最近的邻域启发产生的一个路径长度。局部更新规则的应用使得相应的信息素轨迹减少，可以有效避免蚂蚁收敛到同一路径。
5.5.4 最大-最小蚂蚁系统
最大-最小蚂蚁系统(Max-min Ant System，MMAS)是对标准蚂蚁系统算法的一个简单修改[8, 9]。它有两个主要特点。首先，每一代最好的蚂蚁才能增加信息素，这就减少了开发并增加了对已知的开采。其次，信息素的量是上下有界的，这起到有相反的作用，也就是说，它增加了探索，因为即使是最糟糕的旅行也保留了非零数量的信息素，即使是最好的旅行也无法获得如此多的信息素，以至于完全控制了蚂蚁的决策。
若一条路径的信息素轨迹明显高于其他路径，停滞现象就会发生，因为在这种情况下蚂蚁更倾向于选择该路径，正反馈机制使得该路径的信息素进一步增强，从而蚂蚁将重复地建立同一个解，对搜索空间的探索停止。因此最大-最小蚂蚁系统对信息素轨迹的最大值和最小值分别施加了τ_min和τ_max限制，从而有
5.5.5 最优-最差蚂蚁系统
鉴于蚂蚁系统搜索效率低和质量差的缺点，提出了一种最优-最差蚂蚁系统(Best-Worst Ant System，BWAS)。该算法的思想是对最优解进行更大限度的增强，而对最差解进行削弱，使得属于最优路径的边与属于最差路径的边之间的信息素差异进一步增大，从而使蚂蚁的搜索行为更集中于最优的附近。\ 该算法主要修改了蚁群系统中的全局更新，当所有蚂蚁完成一次循环后，增加对最差蚂蚁所经历路径的信息素的更新。若(i，j)为最差蚂蚁路径中的一条边，且不是最优蚂蚁路径中的边，则该路径的信息素按如下调整：\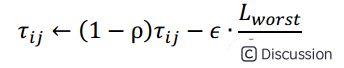 
5.6 代码
``` %% 该函数用于演示基于蚁群算法的三维路径规划算法
%% 清空环境 clc clear
%% 数据初始化
%下载数据 load HeightData HeightData
%网格划分 LevelGrid=10; PortGrid=21;
%起点终点网格点 starty=10;starth=4; endy=8;endh=5; m=1; %算法参数 PopNumber=10; %种群个数 BestFitness=[]; %最佳个体
%初始信息素 pheromone=ones(21,21,21);
%% 初始搜索路径 [path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone, ... HeightData,starty,starth,endy,endh); fitness=CacuFit(path); %适应度计算 [bestfitness,bestindex]=min(fitness); %最佳适应度 bestpath=path(bestindex,:); %最佳路径 BestFitness=[BestFitness;bestfitness]; %适应度值记录
%% 信息素更新 rou=0.2; cfit=100/bestfitness; for i=2:PortGrid-1 pheromone(i,bestpath(i2-1),bestpath(i2))= ... (1-rou)pheromone(i,bestpath(i2-1),bestpath(i2))+roucfit; end
%% 循环寻找最优路径 for kk=1:100
%% 路径搜索
[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,...
pheromone,HeightData,starty,starth,endy,endh);
%% 适应度值计算更新
fitness=CacuFit(path);
[newbestfitness,newbestindex]=min(fitness);
if newbestfitnessend
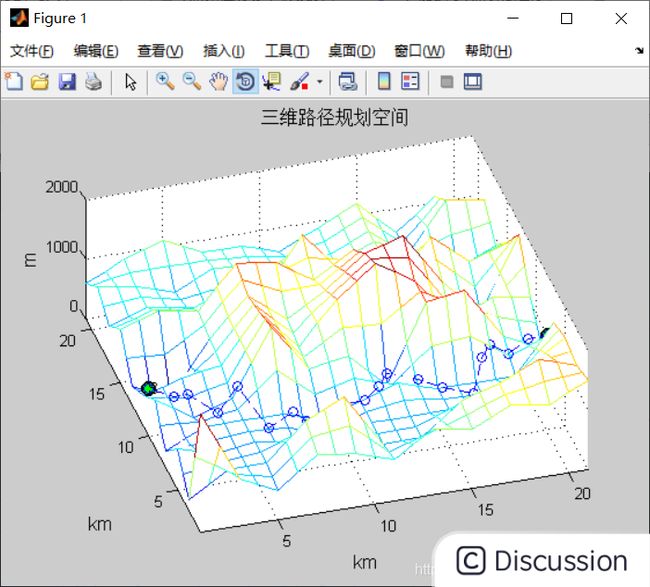
%% 最佳路径 for i=1:21 a(i,1)=bestpath(i2-1); a(i,2)=bestpath(i2); end figure(1) x=1:21; y=1:21; [x1,y1]=meshgrid(x,y); mesh(x1,y1,HeightData) axis([1,21,1,21,0,2000]) hold on k=1:21; plot3(k(1)',a(1,1)',a(1,2)'200,'--o','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','g',... 'MarkerSize',10) plot3(k(21)',a(21,1)',a(21,2)'200,'--o','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','g',... 'MarkerSize',10) text(k(1)',a(1,1)',a(1,2)'200,'S'); text(k(21)',a(21,1)',a(21,2)'200,'T'); xlabel('km','fontsize',12); ylabel('km','fontsize',12); zlabel('m','fontsize',12); title('三维路径规划空间','fontsize',12) set(gcf, 'Renderer', 'ZBuffer') hold on plot3(k',a(:,1)',a(:,2)'*200,'--o')
%% 适应度变化 figure(2) plot(BestFitness) title('最佳个体适应度变化趋势') xlabel('迭代次数') ylabel('适应度值') ```
