贪心c++（结合LeetCode例题）

目录

前言 

LeetCode455分发饼干

思考 

算法思路

LeetCode376摆动序列 

思考

思路

 代码

---

前言 

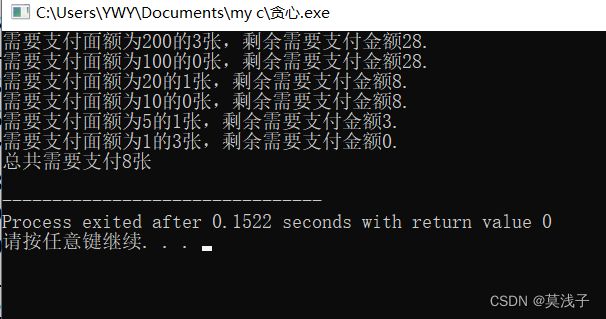
有1元，5元10，元，20元，100元，200，元的钞票无穷多张。先使用这些钞票支付x元支付x元，最少需要多少张？

列如,X= 628

最佳支付方法

3张200的，一张20的，1张5块的，3张一块的，共需要8张

直觉告诉我们：尽可能的多实用面值较大的钞票

贪心：遵循某种规律，不断贪心的选取当前最优策略的算法设计方法

为什么这么做是对的，面额为1元，5元，10元，20元，100元，200元，任意面额是比自己小的面额的倍数关系。

所以当使用一张较大面额的钞票时，若用较小面额钞票替换，，一定需要更多的其他面额钞票。

如10 = 5  + 5

故当前最优解即为全局最优解，贪心成立

思考：如果增加7元面额，贪心还成立吗？（不成立，不满足倍数关系，可以用动态规划解决）

代码：

#include 
using namespace std;
int main()
{
	int rmb[] = {200,100,20,10,5,1};
	int num = 6;     //六种面值 
	int x = 628;
	int count = 0;
	for(int i =0 ;i < num;i++)
	{
		int use = x/rmb[i];
		count += use;
		x = x - rmb[i] * use;
		printf("需要支付面额为%d的%d张，",rmb[i],use);
		printf("剩余需要支付金额%d.\n", x); 
	}
	printf("总共需要支付%d张\n",count++);
}

 

下面用六个题目深入了解贪心 

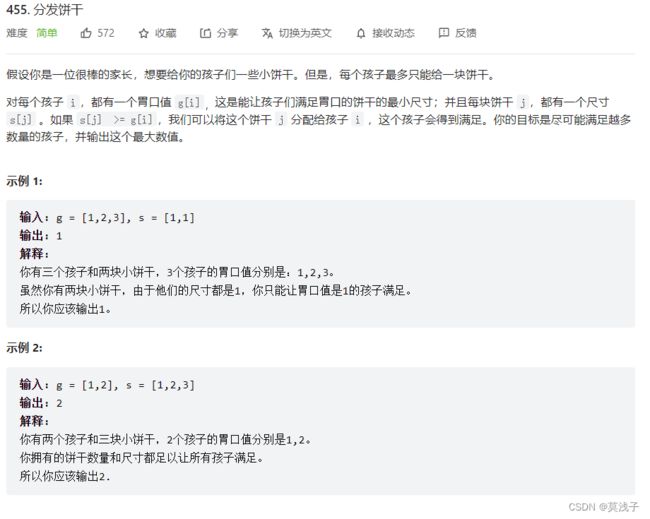
LeetCode455分发饼干

分发饼干

思考： 

做这个题目考虑好俩个问题

第一： 当某个孩子可以被多个饼干满足时，是否需要优先用某个饼干满足这个孩子

第二：当某个饼干可以满足多个孩子时是否需要优先满足某个孩子

为了让更多孩子得到满足有如下规律

1：某个饼干不能满足某个孩子，则饼干也不一定满足需求因子更大的孩子；

2：某个孩子可以更小的饼干满足，没必要用更大的糖果满足，因此可以保留更大的饼干满足需求因子更大的孩子（贪心）

3：孩子的需求因子更小更容易满足，姑优先从需求因子小的孩子尝试，可以得到正确的结果

算法思路：

1、将g与s从小到大排序

 2、从小到大的顺序使用各个饼干尝试是否可以满足某个孩子，每个饼干只尝试1次，若尝试成功，则换一个孩子尝试，知道发现没更多孩子或者没更多的的饼干，循环结束

代码：

class Solution {
public:
    int findContentChildren(vector& g, vector& s) {
        sort(g.begin(),g.end()); 
        sort(s.begin(),s.end());
        int child = 0; //代表满足几个孩子
        int bis = 0;   //代表尝试几个饼干
        while(child < g.size() && bis 

LeetCode376摆动序列 

376. 摆动序列

思考：

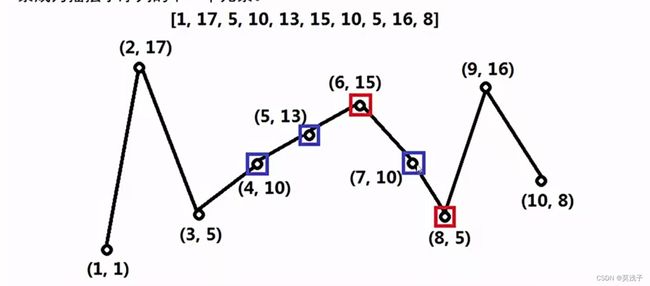
[1,17,5,10,13,15,10,5,16,8],整体不是摇摆序列，观察该序列前六位：[1,17,5,10,13,15]橙色部分为上升段：

其中它的三个子序列是摇摆序列：

[1,17,5,10...]

[1,17,5,13...]

[1,17,5,15...]

在不清楚原始第七位是什么情况下，只看前六位，摇摆子序列的第四位从10,13,15中选择一个数

思考选则那个好

我们的目的是希望第七位成为摇摆序列的概率更大，，应该尽可能的选择大的更大的，所以选择15

思路

状态机 

 代码

class Solution {
public:
    int wiggleMaxLength(vector& nums) {
        if (nums.size() < 2){
            return nums.size();
        }
        static const int BEGIN = 0;
        static const int UP = 1;
        static const int DOWN = 2;
        int STATE = BEGIN;
        int max_length = 1;
        for(int i = 1;i < nums.size();i ++){
            switch(STATE){
                case BEGIN:
                if(nums[i-1] < nums[i]){
                    STATE =UP;
                    max_length ++;
                }
                else if(nums[i-1] > nums[i]){
                    STATE = DOWN;
                    max_length++;
                }
                break;
                case UP:
                if(nums[i-1]>nums[i]){
                    STATE =DOWN;
                    max_length++;
                }
                break;
                case DOWN:
                if(nums[i-1] < nums[i]){
                    STATE =UP;
                    max_length++;
                }
                break;
            } 
            
        }
        return max_length++;

    }
};