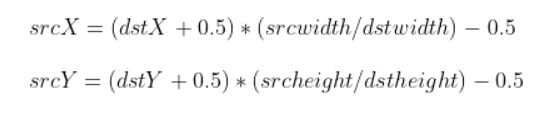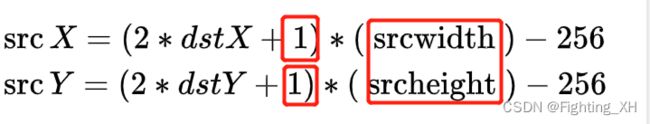基于FPGA的双线性插值算法设计与modelsim分析

前言

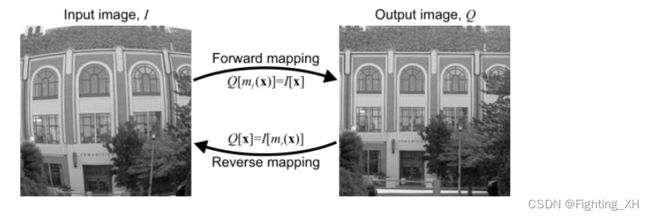
• 在视频图像几何校正或图像配准坐标系转换中，往往需要进行缩放、旋转、透视变换等几何变换操作。要想进行缩放旋转操作，就要得到输入输出图像之间的映射关系，也可称之为几何变换关系。

• 输入和输出像素之间的映射可以用两种不同的方式进行定义，分别是前向映射和逆向映射：
  

• 几何变换的基本结构，包括两种如下左图的前向映射和右图的逆向映射：
  

• 前向映射适合于处理流输入，例如 来自一个摄像机的输入，其每个输入像素 能被映射到 指定输出图像中的位置。

• 逆向映射更适合于产生数据流输出，例如图像数据流输出到显示器，因为对于每个输出像素，逆向映射指定了 像素值来自于 输入图像的什么位置

• 地址的话，一般由行列计数器提供，通过行列计数器获得某点坐标，从而根据二维坐标到一维地址的转换计算得到地址。

• 但是按照这种映射关系，输出图像的像素可能被映射到输入图像的非整数坐标上，因此需要采用插值技术。

---

前向映射的缺点：通过输入位置和相应映射关系来求输出位置，那么当得到非整数输出像素位置的时候，就需要进行四舍五入等，那么会出现如下的问题：
1、当缩放变换系数大于1（放大图像）的时候，四舍五入导致出现空洞，让映射后的一些输出位置没有像素值

2、四舍五入导致像素覆盖，映射后的几个输入像素可能被映射到同一个输出像素位置，那么后一个输出像素值会将前一个覆盖
除此之外，还有一个缺点是输出图像某点像素值不能直接得到，需要遍历输入图像的所有像素值，对其进行坐标变换，分配像素值到整数位置，才能得到输出图像各像素点的像素值。

---

结论：相比前向映射，逆向映射法更直观。对于逆向映射来说，我们知道输出图像上整数点位置(x’,y’)在变换前位于输入图像上的位置(x,y)，一般来说这是个非整数点位置，利用其周围整数像素位置以及对应的像素值（双线性插值使用周围四个整数像素位置）进行插值，就得到了该点的像素值。我们遍历输出图像，经过坐标变换、插值两步操作，我们就能将其像素值一个个地计算出来，因此逆向映射又叫图像填充映射。如下图所示：

1、几种常见插值类型

1.1 最邻近插值

网上有很多解释，可自己查阅

• 优缺点：最简单但锯齿严重
• 基本原理：选择距离期望位置最近的像素进行填补（相当于最近像素的复制粘贴）

最近邻采用最常见的坐标系，以图像的左上角为原点（0，0）；假如我们已知源图像src大小为3 * 3，且知道3 * 3图像内9个点的像素值，现在将src源图像扩大成4*4的目标图像dst，并将对应的像素值填入，在填入对应像素值的时候有如下公式（1）：

> srcX = dstX* (src_Width/dst_Width) 
>                                                                           
> srcY = dstY * (src_Height/dst_Height)

src_Width / ds_tWidth 和 src_Height / dst_Height = 3/4 ，表示两幅图像的长宽边长比。
dstX和dstY我们可以根据目标图像得到，代表目标图像中每个点的横纵坐标。
因此根据dstX和dstY、以及边长比，即可算出对应的源图像坐标，将对应的像素值读出进行填补即可。

---

举例：

目标图像左上角（0，0），带入上述公式，即可找到对应源图像中的坐标（0*（3/4），0*（3/4））=（0，0），因此目标图像（0，0）位置对应的像素值就是源图像（0，0）点对应的像素值2。
同理计算目标图像（0，1）点对应源图像中的（0，3/4）位置，在源图像中像素坐标值都是整数，因此这里的小数3/4需要四舍五入，为（0，3/4）=（0，0.75） = （0，1），因此对应像素值为38。
依次计算，最终可得到4*4图像的全部像素值，此时就实现了图像的最邻近插值放大。

---

总结：通过上述插值可知，当遇到浮点数的时候直接四舍五入取值，拿0.75来说，我们直接取1，这样就会出现较大的误差。因此我们采用距离权重的方式来减少这种误差。既然0.75位于0和1直接，我们即可采用0.75到0，1的距离来分配权重，最终通过整数位置的像素值，得到浮点数0.75处的像素值，这也称为线性插值。

1.2 双线性插值

上述介绍了最邻近插值，误差较大，我们引入了距离权重。将一个浮点数坐标（i + u ，j + v）根据权重分配到距离其最近的四个整数坐标上，进而通过这四个整数坐标的像素值，来得到该浮点坐标的像素值。

• 核心思想：分别在xy两个方向上进行一次插值，即可得到浮点坐标。距离越远权重越小。

---

双线性插值公式（2）：

其中i j 表示浮点数的整数部分，u v表示浮点数的小数部分。 (i+u,j+v) 最近的原图像中的整数坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)。

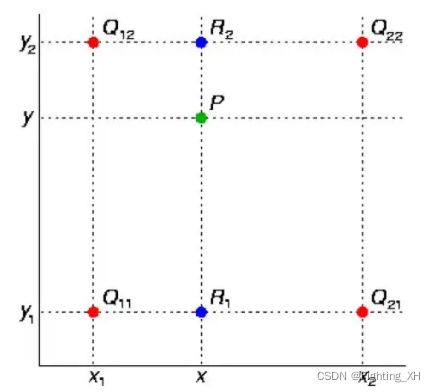
比如下图所示，已知四个红色点的像素值且为整数，求最终落在非整数位置的P的像素值。我们可以先在x方向上进行插值，得到插值结果R1和R2，然后在y方向上继续进行插值，即可得到插值点P。因此当我们知道四个整数坐标以及它们的像素值时，即可根据双线性插值公式，计算出P点的像素值。

---

1.2.1 原点选取的问题

上述我们所讲的原点都是图像的左上角，所以其坐标的计算都由公式（1）得到，这里存在一个问题，当33图像扩大成55，对于5*5图像来说，中心坐标是（2，2），用公式（1）计算出对应的源坐标是（1.2，1.2），但相对于源图像来说，其中心坐标是（1，1），因此我们插值的时候所利用的图像像素整体偏右下，而不是均匀地分布整个图像，为了均匀分布整个图像，我们在取原点的时候，不取左上角，而是取中心对齐的方式来插值，因此源坐标和目标坐标之间的映射关系变成公式（3）：

> SrcX = (dstX+0.5)* (src_Width/dst_Width) -0.5 　
> 
> SrcY = (dstY+0.5) * (src_Height/dst_Height)-0.5

此时将目标图中心坐标（2，2）带入，得到对应的源图像坐标（1，1），和源图像中心坐标重合，即可均匀的分布与整幅图像。

1.3 双三次插值

• 效果更平滑，和双线性插值类似，只不过用相邻16个点，复杂且消耗资源多。
• 一般来说，双线性插值是一个折中选择。

2、FPGA实现双线性插值

2.1 准备工作

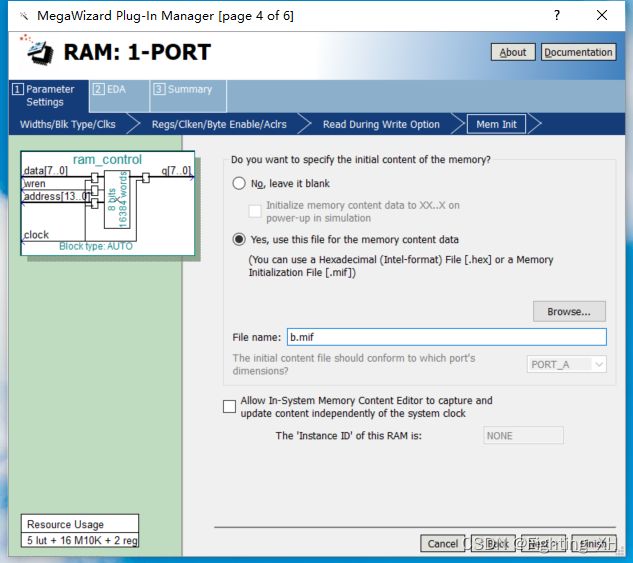
• 准备100*100的mif文件，将其提前存储在RAM中
• 用双线性插值来实现100 * 100图像到256* 256图像的放大操作。
• 双线性插值公式

2.2 实现的难点

• 算法中小数部分到底该如何处理（定点化处理，注意精度问题）
• 如果求出插值公式中的系数，以及周围四个点的坐标
• 求出四个点之后，为加快速度，如何将四个点的像素值同时读出

2.3 整体的RTL图

• 上图可看到，包含五个模块：坐标转换模块，内存管理模块，双线性插值计算模块，分频模块，VGA显示模块。重点看前三个模块。

2.3.1 坐标转换模块

主要工作：得到浮点数（i + u ，j +v）的整数部分的值 i j ；得到四个插值系数 u ， 1-u ，v ， 1-v
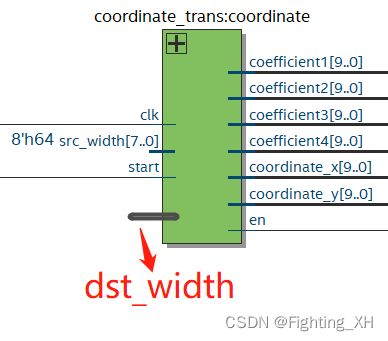
模块接口：
我这里dst_width直接带入的数值，其实可以引出该信号并赋值，更直观。通过src_width和dst_width来计算源图像x y坐标。

2.3.1.1 源图像和目标图像坐标之间的映射关系

• 为达到更好的效果采用优化后的公式（3），也就是以中心为原点插值的方式：
  

2.3.1.2 小数部分的处理

• 我们采用浮点数定点化处理的方式来处理小数部分，因为要目标图像的长宽为256*256，因此需要扩大512倍（放大到不含小数），才能没有小数部分，所以公式改变：

2.3.1.3 整数和小数部分的表示以及最近的四个整数点坐标

• 扩大了512倍相当于右移9位即可去掉小数部分，因此低9位即可表示小数部分，我们定义浮点数为20位，其中整数部分占高10位，那么低10位给小数部分。（多给小数部分一位的原因：10位才可表示最大值512，所以小数部分的第10位需要补0）

 //高10位为整数部分
assign coordinate_x = src_x[19:10];   // i
assign coordinate_y = src_y[19:10];   // j

 //低10位为小数部分，但本来小数部分是9位，因此高位补0
assign coordinate_xx = {1'b0,src_x[8:0]};  //u
assign coordinate_yy = {1'b0,src_y[8:0]};  //v

2.3.1.4 插值公式系数的表示

• 系数包含，u，1-u，v，1-v。因为扩大了512倍数，所以1-u，变成了512-扩大后的小数部分的u

 assign coefficient2 = {1'b0,src_x[8:0]};  //u

assign coefficient1 = 'd512 - coefficient2;   // 1-u

assign coefficient4 = {1'b0,src_y[8:0]}; //v

assign coefficient3 = 'd512 - coefficient4; //1-v

2.3.2 内存管理模块

• 采用4个RAM来解决同时读取四个点对应像素的问题
• 调用IP核的方法，将之前的mif文件存储进去即可
  

2.3.2.1 获得距离浮点坐标最近的四个整数坐标

（i，j）=  （srcX[19:10] ，srcY[19:10]）;

（i+1，j） = （srcX[19:0] + 'd1，srcY[19:0]）;

（i，j+1） = （srcX[19:0]，srcY[19:10] + 'd1）；

（i+1，j+1） = （srcX[19:0] + 'd1 ，srcY[19:10] + 'd1）； 

有了四个整数坐标，即可将二维坐标转换成一维地址，分别从四个存储里面读对应的像素值：

assign address_bx  = (coordinate_x == width)?coordinate_x + coordinate_y*src_width - 'd1:coordinate_x + coordinate_y*src_width;
assign address_bx1 = (coordinate_x == width)?address_bx:address_bx + 'd1;
assign address_by  = (coordinate_y==width)?address_bx:coordinate_x + (coordinate_y+'d1)*src_width;
assign address_by1 = (coordinate_x == width)?address_by:address_by + 'd1;

2.3.3 插值公式代入计算模块

目前是插值系数，以及四个整数坐标对应的像素值都已经有了，因此
代入公式：

assign data_1 = coefficient1*coefficient3*doutbx;  //(1-u)*(1-v)*f(i,j)

assign data_2 = coefficient2*coefficient3*doutbx1;//u*(1-v)*f(i+1,j)

assign data_3 = coefficient1*coefficient4*doutby;//(1-u)*v*f(i,j+1)

assign data_4 = coefficient2*coefficient4*doutby1;//u*1-v*f(i+1,j+1)
 

将四个data进行相加：

assign data_a = data_1 + data_2;
assign data_b = data_3 + data_4;
assign data_oq = data_aq + data_bq;

因为扩大了512倍数，因此还要将结果缩小512倍。所以最终的结果我们要取高8位。

 data_o <= data_oq[25:18];

3、仿真波形

该设计计算量大，不便于仿真数值的查看，因此我们将计算出的数据以txt文本的方式，导出，然后用matlab读取txt文档，直接进行图像的显示。

导出方式：在tb文件中添加如下代码

`timescale 10 ns/ 10 ps

module bilinear_tb();

		reg[7:0] save_data[0:256*256-1];  //表示有65536个8位的图像数据
		reg clk;

		reg start; 
																	
		wire [7:0]  VGA_RGB;
		wire VGA_BLK;
		wire hsync;
		wire vsync;
		wire en_o;


//实例化顶层文件
bilinear i1 (
	
			.clk     (clk),
			.start   (start),
			.VGA_RGB   (VGA_RGB),
			.VGA_BLK (VGA_BLK),
			.hsync   (hsync),
			.vsync   (vsync),
			.en_o(en_o)

		);

initial                                                
begin                                                                        
        clk     =1;
       start    =0;
       #10;
       start    = 1;		 
end    
//产生时钟激励
always #1 clk  =~clk;  

//打开post_img.txt文件
//---------------------------------------------------
integer post_img_txt;

initial begin
    post_img_txt = $fopen("post_img.txt");
end

//像素写入到txt中
//---------------------------------------------------
reg [20:0] pixel_cnt; 

always @(posedge clk) begin
    if(!start) begin
        pixel_cnt <= 0;
    end
    else if(en_o) begin
        pixel_cnt = pixel_cnt + 1;
        $fdisplay(post_img_txt,"%h",VGA_RGB);
		
        if(pixel_cnt == 65536)
            $stop;
    end
end
                                         
endmodule

txt文档用matlab处理，以生成相应图片：

fid0=fopen('savedata.txt','r');    %读入所需要的txt文件
[a,count]=fscanf(fid0,'%x');  %a为data.txt文件数据读入的矩阵，以16进制形式，count为该矩阵元素个数
b=reshape(a,256,256);       % 构建成100*100的矩阵形式     

c=b';           %   需要再转置一次方为图片行列方向的矩阵  

imshow(c,[]);    %显示图片  
title('verilog插值后的图像')  

---

当加入VGA模块的时候，使用上述方法出现问题，因此tb中的计数器是顺序的，因此像素也是按顺序逐脉冲的写入，而对于VGA显示来说，它有行场消隐时间，因此采用逐脉冲顺序写入的方式，会出现无用的像素点，搞清楚原因后没有继续修改，因此如果加上了VGA模块，我们只需要调用锁相环，提供25Mhz时钟，然后上板验证即可。
代码

参考