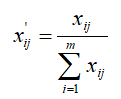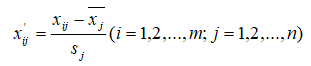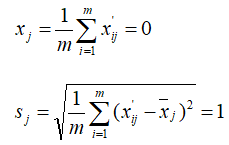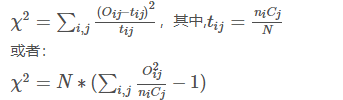python预处理是先标准化数据还是先处理分类特征_数据预处理-数据集成与数据变换...

概况起来，常遇到的数据存在噪声、冗余、关联性、不完整性等。本章将考虑这些问题，在使用算法学习之前，首先需要对数据进行分析，根据数据的不同情况，采用不同的方法对数据进行预处理，数据预处理常见的方法如下：

1. 数据清理：主要是指将数据中缺失的值补充完整、消除噪声数据、识别或删除离群点并解决不一致性。主要是达到如下目标：将数据格式标准化，异常数据清除，错误纠正，重复数据的清除。

2. 数据集成：主要是将多个数据源中的数据进行整合并统一存储。

3. 数据变换：主要是指通过平滑聚集，数据概化，规范化等方式将数据转换成适用于数据挖掘的形式。

4. 数据归约：数据挖掘时往往数据量非常大，因此在少量数据上进行挖掘分析就需要很长的时间，数据归约技术主要是指对数据集进行归约或者简化，不仅保持原数据的完整性，并且数据归约后的结果与归约前结果相同或几乎相同。

这些数据处理技术在数据挖掘之前使用，然后才能输入到机器学习算法中进行学习。这样大大提高了数据挖掘模式的质量，降低实际挖掘所需要的时间

0x00数据集成

我们日常使用的数据来源于各种渠道，有的是连续的数据，有的是离散数据、有的是模糊数据，有的是定性数据，有的是定量数据。数据集成就是将多文件或者多数据库中的异构数据进行合并，然后存放在一个统一的数据库中进行存储。在进行数据的集成过程中，一般需要考虑以下问题：

实体识别

主要指数据源来源不同，其中多的概念定义不一样

同名异意：数据源A的某个数据特征的名称和数据源B的某个数据特征是一样的但是表示的内容不一样。

异名同义：数据源A的某个特征的名称和数据源B的某个特征名称不一样，但是表达的内容不一样。

单位不统一：不同地数据源记录的单位不一样，比如统计身高、一个数据源以m为单位，一个使用英尺

冗余属性

指数据中存在冗余，一般分为一下两种

同一属性出现多次，比如两个数据源都记录每天的最高温度和最低温度，当数据集成时，就出现了两次。

同一属性命名不一致而导致数据重复

数据不一致

编码使用的不一致问题和数据表示的不一致问题，比如旧的***号15位，而新的时18位

0x01数据变换

数据变换是指将数据转换或统一成适合于机器学习的形式。就像人类学习一样，需要将采集的外部数据转换成我们可以接收的形式。

由于实际过程中采集的各种数据，形式多种多样，格式也不一致，这些都需要采用一定的数据预处理，使得他们符合机器学习的算法使用。

数据变换常用方法如下：

使用简单的数学函数对数据进行变换

对采集的原始数据使用各种简单的数学函数进行转换，常见的函数包括平方、开方、取对数、差分运算等(压缩变大或者压缩变小)。

归一化

特征归一化也叫做数据无量纲化，主要包括：总和标准化、标准差标准化、极大值标准化、极差标准化。这里需要说明的是，基于树的方法是不需要进行特征归一化的，例如GBDT，bagging、boosting等等，而基于参数的模型或基于距离的模型，则都需要进行特征归一化。

总和标准化

总和标准化处理后的数据介于(0,1)之间，并且它们的和为1。总和标准化的步骤和公式也非常简单：分别求出各聚类要素所定义的数据的总和，以各要素的数据除以该要素的数据总和，即：

经过总和标准化处理后所得的新数据满足：

标准差标准化

标准差标准化公式如：

其中

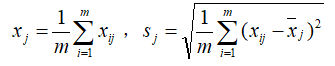标准差标准化处理后所得到的新数据，各要素(指标)的平均值0，标准差为1，即：

极大值标准化

结果极大值标准化的公式如下所示：

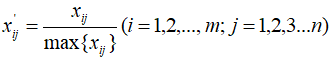极大值标准化后的新数据，各要素的最大值为1，其余各项都小于1。

对稀疏数据进行中心化会破坏稀疏数据的结构，这样做没有什么意义，但可以对稀疏数据标准化，极大值标准化就是为稀疏数据设计的，同时这也是一种常用的方法，Python中极大值标准化为MaxAbsScaler()，如果要使用Python中标准差标准化(StandardScaler)则需要设置with_centering = False，否则将破坏数据稀疏性。

极差标准化(区间放缩法，0-1标准化)

极差标准化的计算公式如下：

经过极差标准化处理后的新数据，各要素的极大值为1，极小值为0，其余数值均在0与1之间。这里的min{x_ij}和max{x_ij}指的是和x_ij同一列的最小值和最大值。

如果数据中有离群点，对数据进行均值和方差的标准化效果并不好，这时候可以使用robust_scale和RobustScaler作为代替，它们有对数据中心化和数据的缩放鲁棒性更强的参数。

连续特征变换

连续特征变换的常用方法有三种：基于多项式的数据变换、基于指数函数的数据变换、基于对数函数的数据变换。连续特征变换能够增加数据的非线性特征捕获特征之间的关系，有效提高模型的复杂度。

#encoding=utf-8

"""

生成多项式特征与自定义函数(如：log等)

在输入特征中增加非线性特征可以有效提高模型的复杂度，其中最常用的是多项式特征

matrix =

[[0 1 2]

[3 4 5]

[6 7 8]]

当degree = 2时，以第二行为例：

[1 3 4 5 3*3 3*4 3*5 4*4 4*5 5*5]

当degree = 3时，以第二行为例：:

[1 3 4 5 3*3 3*4 3*5 4*4 4*5 5*5 3*3*3 3*3*4 3*3*5 4*4*3 4*3*5 5*5*3 4*4*4 4*4*5 4*5*5 5*5*5]

"""

import numpy as np

from sklearn.preprocessing import PolynomialFeatures

from sklearn.preprocessing import FunctionTransformer

"""生成多项式"""

X = np.arange(9).reshape(3,3)

print(X)

ploy = PolynomialFeatures(2)

print(ploy.fit_transform(X))

ploy = PolynomialFeatures(3)

print(ploy.fit_transform(X))

"""自定义转换器"""

X = np.array([[0,1],[2,3]])

transformer = FunctionTransformer(np.log1p) #括号内的就是自定义函数

print(transformer.fit_transform(X))

transformer = FunctionTransformer(np.exp)

print(transformer.fit_transform(X))

输出结果：

(env_default) PS F:\workspace> python .\test.py

[[0 1 2]

[3 4 5]

[6 7 8]]

[[ 1.  0.  1.  2.  0.  0.  0.  1.  2.  4.]

[ 1.  3.  4.  5.  9. 12. 15. 16. 20. 25.]

[ 1.  6.  7.  8. 36. 42. 48. 49. 56. 64.]]

[[  1.   0.   1.   2.   0.   0.   0.   1.   2.   4.   0.   0.   0.

0.

0.   0.   1.   2.   4.   8.]

[  1.   3.   4.   5.   9.  12.  15.  16.  20.  25.  27.  36.  45.

48.

60.  75.  64.  80. 100. 125.]

[  1.   6.   7.   8.  36.  42.  48.  49.  56.  64. 216. 252. 288. 294.

336. 384. 343. 392. 448. 512.]]

[[0.         0.69314718]

[1.09861229 1.38629436]]

[[ 1.          2.71828183]

[ 7.3890561  20.08553692]]

(env_default) PS F:\workspace>

连续属性离散化

1. 离散化技术分类

连续属性的离散化方法也可以被称为分箱法，即将一组连续的值根据一定的规则分别放到其术语的集合中。

离散化技术可以根据如何对数据进行离散化加以分类，可以根据是否使用类信息或根据进行方向(即自顶向下或自底向上)分类。

如果离散化过程使用类信息，则称它为监督离散化(superviseddiscretization)；否则是非监督的(unsupervised)。

如果首先找出一点或几个点(称作分裂点或割点)来划分整个属性区间，然后在结果区间上递归地重复这一过程，则称它为自顶向下离散化或分裂。自底向上离散化或合并正好相反，首先将所有的连续值看作可能的分裂点，通过合并相邻域的值形成区间，然后递归地应用这一过程于结果区间。

2. 无监督离散化与监督离散化

根据数据是否包含类别信息可以把它们分成有监督的数据和无监督的数据。有监督的离散化要考虑类别信息而无监督的离散化则不需要。

无监督离散化

假设属性的取值空间为

 ，离散化之后的类标号是 

 ，则无监督离散化的情况就是X已知而Y未知。以下介绍几种常用的无监督离散化方法：

(1) 等宽算法

根据用户指定的区间数目K，将属性的值域[Xmin−Xmax]划分成K个区间，并使每个区间的宽度相等，即都等于Xmax−XminK。缺点是容易受离群点的影响而使性能不佳。

(2) 等频算法

等频算法也是根据用户自定义的区间数目，将属性的值域划分成K个小区间。他要求落在每个区间的对象数目相等。譬如，属性的取值区间内共有M个点，则等频区间所划分的K个小区域内，每个区域含有MK个点。

(3) K-means聚类算法

首先由用户指定离散化产生的区间数目K，K-均值算法首先从数据集中随机找出K个数据作为K个初始区间的重心；然后，根据这些重心的欧式距离，对所有的对象聚类：如果数据x距重心Gi最近，则将x划归Gi所代表的那个区间；然后重新计算各区间的重心，并利用新的重心重新聚类所有样本。逐步循环，直到所有区间的重心不再随算法循环而改变为止。

监督离散化

监督离散化就是事先X和Y均为已知，然后找到某个函数，利用X值对Y值做预测。可以建立回归或者分类模型。

以下介绍的自下而上或者自上而下的分类方法都属于监督离散化方法。

3. 齐次性的卡方检验

在介绍两种基于卡方检验的离散化算法之前，先来介绍一下齐次性的卡方检验。

数据：有rr个总体。

从每个总体中抽取一个随机变量，记第ii个样本含有的观测数是

， 每个样本的每个观测值可以归为cc个不同类别中的一类。记Oij为样本ii的观测值归入类j的个数，所以， 

 对于所有的样本i，将数据排列成以下的r∗c

| 类1 | 类2   | ⋯⋯ | 类c    | 总和|

| -------- | -------- | -------- | -------- | -------- |

| 总体1|  O11 | O12|  ⋯⋯  | O1c   | n1|

| 总体2   | O21|  O22 | ⋯⋯|   O21 | n2|

| ⋯⋯|   ⋯⋯|     ⋯⋯  | ⋯⋯    | ⋯⋯    | ⋯⋯|

| 总体r   | Or1   | Or2   | ⋯⋯|   Orc | nr|

| 总和    | C1    | C2    | ⋯⋯    | Cc    | N|

假设：

记pijpij为随机取到第ii个总体划分为第jj类的概率，j∈[i,c]i∈[1,r],。

H0:同一列中所有的概率相等(即对任意的j，p1j=p2j=⋯=prjp1j=p2j=⋯=prj)。

H1:每列中至少存在两个概率不相等(即给定j，存在i和k，使得pij≠pkj)。

检验统计量χ2为：

零分布：

| 吸烟    | 不吸烟|  总计|

| -------- | -------- | -------- |

| 男 | 20    | 5 | 25|

| 女 | 10|   15  | 25|

| 总计    | 30|   20  | 50|

首先假设H0：性别和吸烟相关。

根据公式求得χ2=8.33，自由度为1，查表可得p值小于0.005，所以拒绝原假设。

4. 自上而下的卡方分裂算法

该分裂算法是把整个属性的取值区间当做一个离散的属性值，然后对该区间进行划分，一般是一分为二，即把一个区间分为两个相邻的区间，每个区间对应一个离散的属性值，该划分可以一直进行下去，直到满足某种停止条件，其关键是划分点的选取。

分裂步骤：

依次计算每个插入点的卡方值，当卡方值达到最大时，将该点作为分裂点，属性值域被分为两块。

然后再计算卡方值，找到最大值将属性值域分成三块。

停止准则：

当卡方检验显著，即pp值

当卡方检验不显著，即pp值⩾α⩾α时，停止分裂区间；

5. ChiMerge算法

ChiMerge算法是一种基于卡方值的自下而上的离散化方法。和上一种算法正好相反。

分裂步骤：

第一步：根据要离散的属性对实例进行排序：每个实例属于一个区间

第二步：合并区间，计算每一对相邻区间的卡方值

停止准则：

当卡方检验不显著，即pp值⩾α时，继续合并相邻区间；

当卡方检验显著，即pp值

6. 基于熵的离散化方法

本方法也是一种自上而下的离散化方法。首先，定义一下熵的概念：

其中，

是第i个区间中类jj的概率。

该划分的总熵e是每个区间的熵的加权平均：

其中

是第i个区间的值的比例，n是区间个数。

划分过程：

首先将属性的取值值域按照值得大小排序。 把每个值看作是可能的分割点，依次把区间分成两部分计算它们的熵值，取熵值最小的作为第一次划分点。

然后选取一个区间，通常选择熵值最大的区间重复此过程。

当区间个数达到用户指定的个数或某个用户指定的终止条件则停止继续分裂。

本作品采用《CC 协议》，转载必须注明作者和本文链接