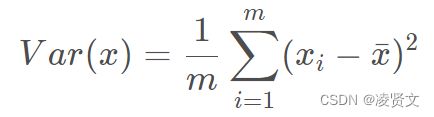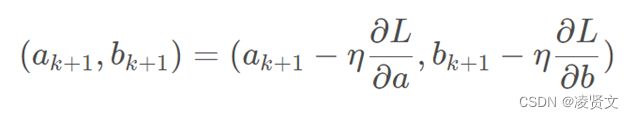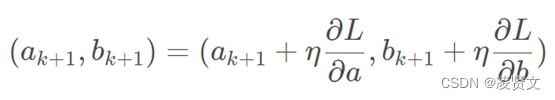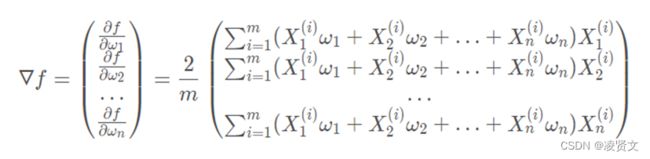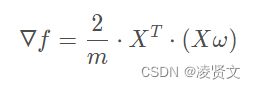机器学习:(PCA)主成分分析法及应用(spss)
目录
1.1、主成分分析法简介
1.2、主成分分析法的意义
1.3、主成分分析法的思想
1.4、主成分分析法的步骤
2.1、导入数据
2.2、生成图表
3.1、PCA算法梯度求解
3.1.1. 梯度上升&梯度下降
3.1.2求梯度
3.2求解第一主成分代码实现
3.2.1 数据准备
3.2.2. 函数实现
3.2.3. 结果可视化
3.3求前n个主成分
一、主成分分析原理
1.1、主成分分析法简介
美国的统计学家斯通(stone)在1947年关于国民经济的研究。他曾利用美国1929—1938年各年的数据,得到了17个反映国民收入与支出的变量要素,例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息外贸平衡等等。在进行主成分分析后,竟以97.4 %的精度,用3个新变量就取代了原17个变量。根据经济学知识,斯通给这三个新变量分别命名为总收入F1、总收入变化率F2和经济发展或衰退的趋势F3。
其最主要的用途在于"降维",通过析取主成分显出的最大的个别差异,发现更便于人类理解的特征。也可以用来削减回归分析和聚类分析中变量的数目。
主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Var(F1)越大,表示F1包含的信息越多。
因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1,F2)=0,则称F2为第二主成分,依此类推可以构造出第三、第四…,第P个主成分。
1.2、主成分分析法的意义
在很多场景中需要对多变量数据进行观测,在一定程度上增加了数据采集的工作量。更重要的是:多变量之间可能存在相关性,从而增加了问题分析的复杂性。
如果对每个指标进行单独分析,其分析结果往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。
1.3、主成分分析法的思想
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
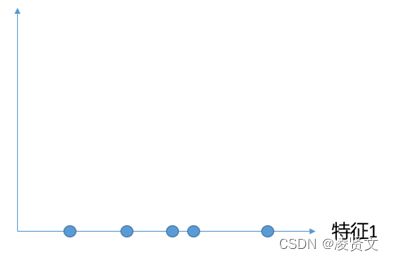
先假设用数据的两个特征画出散点图:
如果我们只保留特征1或者特征2,就存在一个问题,保存特征1还是特征2。
通过上面对两个特征的映射结果可以发现保留特征1(右面)比较好,因为保留特征1,当把所有的点映射到x轴上以后,点和点之间的距离相对较大,也就是说,拥有更高的可区分度,同时还保留着部分映射之前的空间信息。
那么如果把点都映射到y轴上,发现点与点距离更近了,这不符合数据原来的空间分布。所以保留特征1相比保留特征2更加合适,但是这是最好的方案吗?
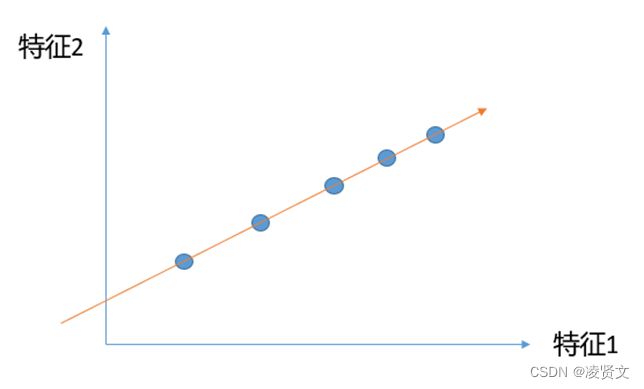
将所有的点都映射到一根拟合的斜线上,从二维降到一维,整体和原样本的分布并没有多大的差距,点和点之间的距离更大了,区分度也更加明显。
所以我们的问题就是找到这样的让样本间距最大的轴。
这里我们给出方差的定义来表示样本之间的间距:
1.4、主成分分析法的步骤
1.根据研究问题选取指标与数据;
2.进行指标数据标准化( SPSS软件Factor过程自动执行);
3.进行指标之间的相关性判定;
4.确定主成分个数m;
5.确定主成分表达式;
6.进行主成分命名;
7.计算综合主成分值并进行评价与研究。
二、运用SPSS进行主成分分析
2.1、导入数据
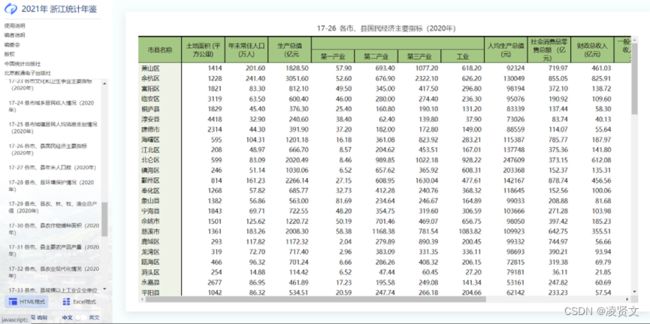
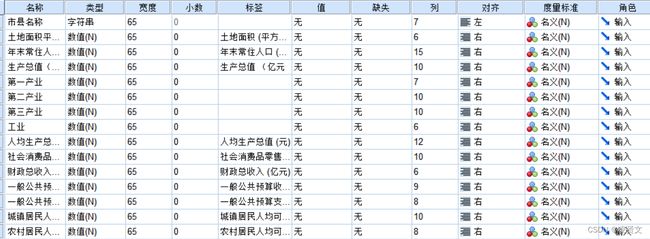
在浙江统计年鉴上下载各市县的国民经济主要指标。
对下载的数据进行一个简单的数据处理。
导入到SPSS软件中;
将数据格式进行修改,除了第一个市县名称,其他都修改为数值格式的类型。
点击降维进行因子分析,将变量选入变量框,选择描述、提取和得分。
2.2、生成图表
SPSS 在调用 Factor Analyze 过程进行分析时, SPSS 会自动对原始数据进行标准化处理, 所以在得到计算结果后的变量都是指经过标准化处理后的变量, 但 SPSS 并不直接给出标准化后的数据, 如需要得到标准化数据, 则需调用 Descriptives 过程进行计算。
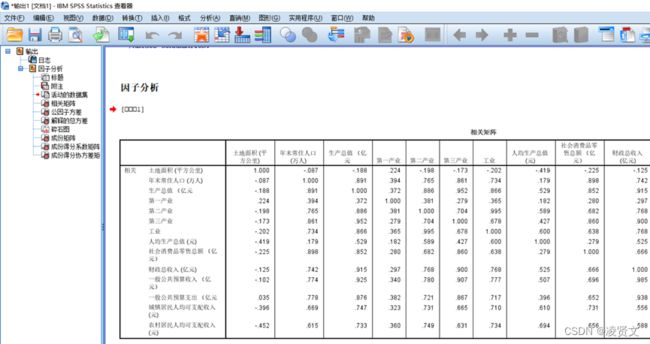
土地面积和土地面积的相关性为1,自己和自己相关性最强;土地面积和年末常住人口的相关性为-0.087,说明两者相关性不强;等等;
从上表可知 GDP 与工业增加值, 第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、地方财政收入这几个指标存在着极其显著的关系, 与海关出口总额存在着显著关系。可见许多变量之间直接的相关性比较强, 证明他们存在信息上的重叠。
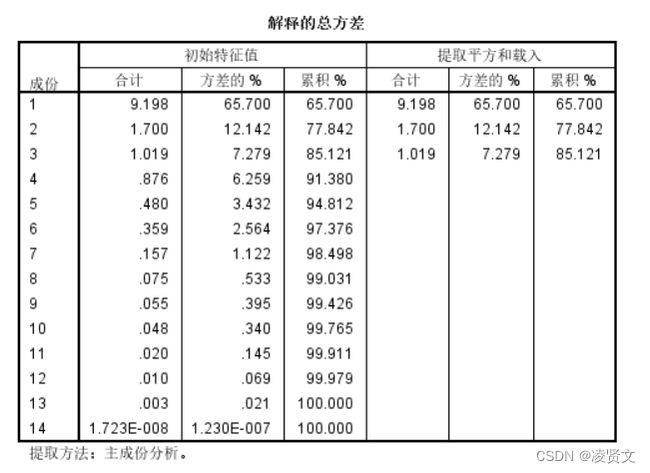
上图:可以看出第一个特征占65.700%,前两个特征累计占77.842%;所以提取3个主成分,即m=3。
下图: 可知 土地面积、GDP、工业增加值、第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、海关出口总额、地方财政收入在第一主成分上有较高载荷, 说明第一主成分基本反映了这些指标的信息; 人均 GDP 和农业增加值指标在第二主成分上有较高载荷, 说明第二主成分基本反映了人均GDP 和农业增加值两个指标的信息。所以提取三个主成分是可以基本反映全部指标的信息, 所以决定用3个新变量来代替原来的14个变量。
最后,用成分矩阵中的数据除以主成分相对应的特征值开平方根便得到三个主成分中每个指标所对应的系数。
三、运用机器学习中的算法进行主成分分析
3.1、PCA算法梯度求解
主成分分析方法(PCA),是数据降维算法。将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,即用较少的综合指标分别代表存在于各个变量中的各类信息,达到数据降维的效果。
所用到的方法就是“映射”:将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。我们要选择的就是让映射后样本间距最大的轴。
其过程分为两步:
1、样本归0
2、找到样本点映射后方差最大的单位向量ω
最后就能转为求目标函数的最优化问题:
对于最优化问题,除了求出严格的数据解以外,还可以使用搜索策略求极值。在求极值的问题中,有梯度上升和梯度下降两个最优化方法。梯度上升用于求最大值,梯度下降用于求最小值。
3.1.1. 梯度上升&梯度下降
梯度下降的思想及推导问题。已知:使损失函数值变小的迭代公式
我们现在要求极大值,则使用梯度上升法。梯度的方向就是函数值在该点上升最快的方向,顺着这个梯度方向轴,就可以找到极大值。即将负号变为正号:
3.1.2求梯度
对PCA算法求解中,对于 PAC 的目标函数:
首先要求梯度。在上式中,ω 是未知数Xi 是非监督学习提供的已知样本信息。因此对f(x) 中ω 的每一个维度进行求导:
对上式进行合并,写成两个向量点乘的形式。更进一步对表达式进行向量化处理
得到梯度为:
通过梯度,可以使用梯度上升法求最大值了。
3.2求解第一主成分代码实现
3.2.1 数据准备
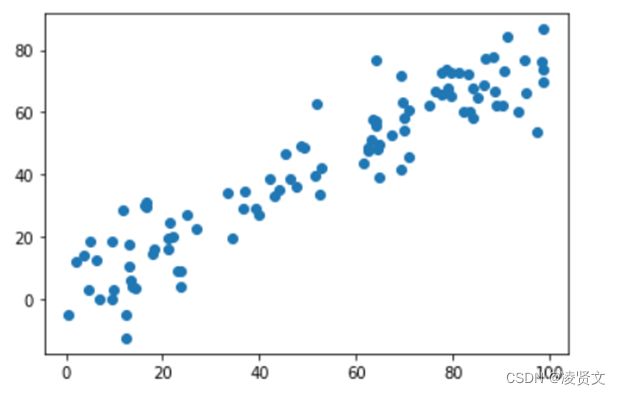
首先准备数据:
import numpy as np
import matplotlib.pyplot as plt
X = np.empty([100,2])
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0., 10., size=100)
plt.scatter(X[:,0],X[:,1])
plt.show()3.2.2. 函数实现
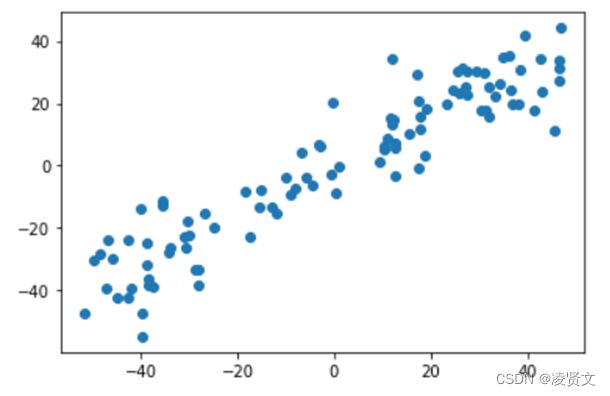
接下来对数据进行主成分分析,第一步是均值归零,定义相应的函数。
将样本进行均值归0(demean),即所有样本将去样本的均值。样本的分布没有改变,只是将坐标轴进行了移动。
其方法是:X表示一个矩阵,每一行代表一个样本,每一个样本的每一个特征都减去这个特征的均值。实现如下:
def demean(X):
# axis=0按列计算均值,即每个属性的均值,1则是计算行的均值
return (X - np.mean(X, axis=0))
X_demean = demean(X)
# 注意看数据分布没变,但是坐标已经以原点为中心了
plt.scatter(X_demean[:, 0], X_demean[:, 1])
plt.show()接下来就是对目标(方差)函数和梯度(导数)函数的定义。
首先定义目标函数:
def f(w,X):
return np.sum((X.dot(w)**2))/len(X)
然后根据梯度公式求梯度:
def df_math(w,X):
return X.T.dot(X.dot(w))*2./len(X)现在对其稍加改造,可以验证我们之前计算的梯度表达式的结果是否正确。
# 验证梯度求解是否正确,使用梯度调试方法:
def df_debug(w, X, epsilon=0.0001):
# 先创建一个与参数组等长的向量
res = np.empty(len(w))
# 对于每个梯度,求值
for i in range(len(w)):
w_1 = w.copy()
w_1[i] += epsilon
w_2 = w.copy()
w_2[i] -= epsilon
res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
return res
对于要求的轴,向量ω,实际上一个单位向量,即要让向量的模为1
因此我们使用np中的线性代数库linalg里面的norm()方法,求第二范数,也就是求算术平方根。
def direction(w):
return w / np.linalg.norm(w)然后就实现梯度上升代码的流程了:gradient_ascent()方法为梯度上升法的过程,在n_iters次循环中,每次获得新的ω,如果新的ω和旧的ω对应的函数f的值的差值满足精度epsilon,则表示找到了合适的ω:
此处,对于每一次计算向量ω之前都要进行单位化计算,使其模为1。
# 梯度上升法代码
def gradient_ascent(df, X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = df_math(w,X)
last_w = w
w = last_w + eta * gradient
w = direction(w) # 将w转换成单位向量
if (abs(f(w,X) - f(last_w,X)) < epsilon):
break
cur_iter += 1
return w
接着使用梯度上升法,先设定一个初始的ω和学习率η :
这里面还需要注意一点:线性回归中,通常将特征系数θ的值设为全部为0的向量。但在主成分分析中w的初始值不能为0。这是因为如果将w=0带入梯度求导的公式中,也是每次求梯度得到的都是没有任何方向的0。所以要设置一组随机数。
initial_w = np.random.random(X.shape[1])
eta = 0.001
然后执行gradient_ascent()方法,计算梯度上升的结果,即要求的轴。
w = gradient_ascent(df_debug, X_demean, initial_w, eta)
# 输出
array([0.76567331, 0.64322965])3.2.3. 结果可视化
进行可视化,轴对应的方向,即将样本映射到该轴上的方差最大,这个轴就是一个主成分(第一主成分):
这样,就求出了二维数据的1个主成分,二维数据映射到一维就足够了。
但是如果是高维数据,可能就要映射到多维上。即求出第n主成分。
3.3求前n个主成分
在实际的降维过程可能会涉及到数据在多个维度的降维,这就需要依次求解多个主成分。
求解第一个主成分后,假设得到映射的轴为ω所表示的向量,如果此时需要求解第二个主成分怎么做?
这需要先将数据集在第一个主成分上的分量去掉,然后在没有第一个主成分的基础上再寻找第二个主成分。
五、总结
本文通过介绍主成分分析的基本原理和思想,利用SPSS和机器学习中的PCA算法进行主成分分析的介绍。
在SPSS中,通过对浙江统计年鉴上各市县的国民经济主要指标进行主成分分析,生成了相关矩阵,总方差的解释,成份矩阵等,得到了3个主成分指标,来表示浙江各市县的GDP指数,用3个变量,替换了原来的14个变量。并且用成份矩阵中的数据除以主成分相对应的特征值开平方根便得到3个主成分中每个指标所对应的系数。
在机器学习的PCA算法中,先通过样本归0,再找到样本点映射后方差最大的单位向量ω ,最后就能转为求目标函数的最优化问题,通过梯度下降方法求出极值,在本文中给出了具体的算法和部分代码,并且将二维数据通过可视化图表展示出来。
六、参考文献
[1]林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005(03):65-69.DOI:10.19343/j.cnki.11-1302/c.2005.03.015.
[2]张文霖.主成分分析在SPSS中的操作应用[J].市场研究,2005(12):31-34.
[3]李艳双,曾珍香,张闽,于树江.主成分分析法在多指标综合评价方法中的应用[J].河北工业大学学报,1999(01):96-99.
[4]张鹏. 基于主成分分析的综合评价研究[D].南京理工大学,2004.
[5]csdn.[Z] 机器学习笔记(九)——数据降维:主成分分析(PCA)
https://blog.csdn.net/weixin_43312354/article/details/105653308