机器学习实践:监督学习-7
机器学习实践:监督学习
1、实验描述
-
本实验通过scikit-learn工具包主要介绍了监督学习概念,并通过实验掌握监督学习中常见的回归和分类算法,理解分类和回归的区别,比较各类分类算法的优劣,能够理解调参在非线性分类中的重要性等内容
-
实验时长:90分钟
-
主要步骤
-
监督学习简介
-
广义线性回归模型简介
-
最小二乘回归
-
广义线性分类模型简介
-
感知机
-
支持向量机
-
非线性支持向量机
-
2、实验环境
-
虚拟机数量:1
-
系统版本:CentOS 7.5
-
Python版本: Python 3.5
3、相关技能
-
Python编程
-
scikit-learn编程
-
监督学习
-
分类和回归
4、相关知识点
-
监督学习
-
广义线性回归模型
-
广义线性分类模型
-
非线性支持向量机
5、效果图
- 感知机模型预测的结果,使用matplotlib进行可视化,结果如下图
- 感知机模型、线性支持向量机模型评分如下
6、实验步骤
6.1监督学习(英语:Supervised learning)是最为常见,且应用最为广泛的分支之一。监督学习是指:利用一组已知类别的样本调整分类器的参数,使其达到所要求性能的过程,也称为监督训练。监督学习是从标记的训练数据来推断一个功能的机器学习任务。训练数据包括一套训练示例。在监督学习中,每个实例都是由一个输入对象(通常为矢量)和一个期望的输出值(也称为监督信号)组成。监督学习算法是分析该训练数据,并产生一个推断的功能,其可以用于映射出新的实例。一个最佳的方案将允许该算法来正确地决定那些看不见的实例的类标签。这就要求学习算法是在一种“合理”的方式下从一种从训练数据到看不见的情况下形成
6.2监督学习问题目前分为两类
6.2.1分类问题:输出为有限个离散变量,布尔值或者定类变量。
6.2.2回归问题:输出为连续变量,一般为实数,也就是一个确切值
6.3常见你的监督学习方法:广义线性模型、支持向量机、k近邻、决策树、朴素贝叶斯、逻辑回归等,本实验中我们主要讲解广义线性模型
6.4广义线性回归模型
6.4.1scikit-learn 中包含的广义线性模型有最小二乘回归、感知机、逻辑回归、岭回归,贝叶斯回归等,由 sklearn.linear_model 模块导入,其中,最小二乘回归、岭回归、贝叶斯回归等是用于解决回归问题。而感知机、逻辑回归被用于解决分类问题,本实验中我们主要讲解最小二乘回归与感知机分类
6.4.2如何使用最小二乘回归完成线性回归
6.4.2.1使用scikit-learn完成相关的问题。
6.4.2.2调用一个机器学习方法构建相应的模型 model,并设置模型参数。
6.4.2.3使用该机器学习模型提供的 model.fit() 训练模型。
6.4.2.4使用该机器学习模型提供的 model.predict() 方法用于预测。
6.4.3开始实验:进入虚拟环境zkbc中(该环境在前面实验中已经创建,如果未创建则可以利用`conda create -n zkbc python=3.5`命令创建该环境即可)
[zkpk@master ~]$ source activate zkbc
(zkbc)[zkpk@master ~]$
6.4.4利用conda安装需要的python模块,这里我们主要用到scikit-learn(需要先安装numpy);安装过程中,命令行询问"Proceed([y]/n)?",输入y继续
(zkbc)[zkpk@master ~]$ conda install numpy=1.11.3
(zkbc)[zkpk@master ~]$ conda install scipy
(zkbc)[zkpk@master ~]$ pip install scikit-learn
6.4.5安装完成后,进入python命令行
(zkbc)[zkpk@master ~]$ python
6.4.6导入scikit-learn的线性模型模块,创建最小二乘回归模型
>>>from sklearn import linear_model
>>>model = linear_model.LinearRegression() # 调用最小二乘回归方法
6.4.7一般平面中两个点可以确定一条直线,使用模型带有的 fit() 方法去拟和2个点。两个点的特征向量分别为 [0, 0], [1, 1] ,对应的目标值为 [2,3]。这里我们使用的模型自带的默认参数进行训练
>>>model.fit ([[0, 0], [1, 1]], [2,3]) # 模型拟合
6.4.8训练时,选择的 [0, 0], [1,1]这两个点恰好在一条直线上,再结合目mode标值想象一下它们的空间位置关系。我们可以使用下面的方法,输出拟合直线权重项和常数项值。
>>>model.coef_
>>>model.intercept_
6.4.10接下来使用训练好的模型对新的输入进行预测,验证模型。
>>>model.predict([[3, 3]])
6.4.11可以看到结果的确和我们预想的一致,也表明我们通过广义线性模型完成了一个基础的线性回归问题
6.5广义线性回归模型中最小二乘回归模型复杂实例
6.5.1上面我们介绍了一种很简单的基础线性回归问题,接下来我们使用该模型来训练一个较为复杂的数据集
6.5.2这里我们使用的scikit-learn模块自带的diabetes糖尿病数据集,该数据集包括442个病人的生理数据及一年以后的病情发展情况。该数据集中的特征值总共10项,如下: 年龄 、性别、体质指数 、血压、s1,s2,s3,s4,s4,s6(六种血清的化验数据);但请注意,以上的数据是经过特殊处理,10个数据中的每个都做了均值中心化处理,然后又用标准差乘以个体数量调整了数值范围。验证就会发现任何一列的所有数值平方和为1
6.5.3这里我们需要使用matplotlib来进行绘图,先使用`exit()`退出python命令行,再利用conda命令安装matplotlib,在询问是否确定时输入y(若已安装则可以跳过此步骤)
>>>exit()
(zkbc)[zkpk@master ~]$ conda install matplotlib
6.5.4安装完成后再次利用python命令进入python命令行
(zkbc)[zkpk@master ~]$ python
6.5.5导入本实验所需的包
>>>import numpy as np
>>>from sklearn import datasets
>>>from sklearn.model_selection import train_test_split
>>>from sklearn import linear_model
>>>import matplotlib.pyplot as plt
6.5.6载入糖尿病数据集,该数据集特征较多,这里选取其中一个特征值,np.newaxis的作用是增加新的维度
>>>diabetes = datasets.load_diabetes()
>>>diabetes_feature = diabetes.data[:, np.newaxis,2]
>>>diabetes_target = diabetes.target
6.5.7利用train_test_split切分数据集为70%训练集,30%测试集,random_state为随机种子数,该数值可自定义,作用是确保每次随机的结果一致
>>>train_feature, test_feature, train_target, test_target = train_test_split(diabetes_feature, diabetes_target, test_size=0.3,random_state=90)
6.5.8创建最小二乘线性回归模型,利用训练集训练数据
>>>model = linear_model.LinearRegression()
>>>model.fit(train_feature, train_target)
6.5.9利用matplotlib绘制训练集黑色散点图和测试集红色散点图
>>>plt.scatter(train_feature, train_target, color='black')
>>>plt.scatter(test_feature, test_target, color='red')
6.5.10利用matplotlib的plot方法绘制拟合直线
>>>plt.plot(test_feature, model.predict(test_feature), color='blue',linewidth=3)
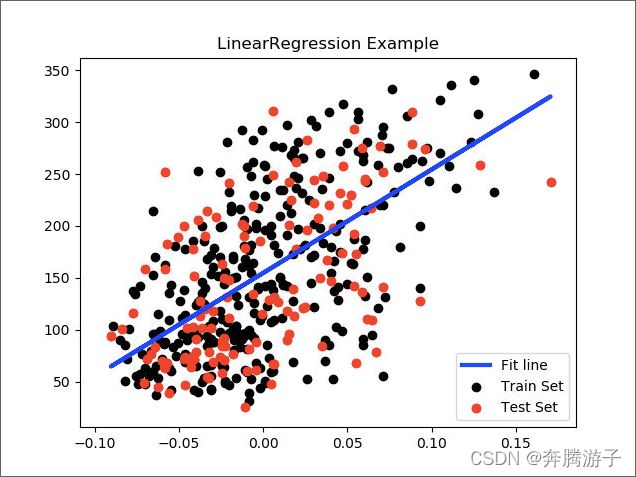
6.5.11利用matplotlib的legend方法和title方法绘制图例和标题
>>>plt.legend(('Fit line', 'Train Set', 'Test Set'), loc='lower right')
>>>plt.title('LinearRegression Example')
6.5.12打印图形查看结果
>>>plt.show()
6.5.13通过图形我们可以直观看到最小二乘回归的进行拟合的结果
6.5.14关闭图形,回到python命令行界面
6.6广义线性分类模型 :
6.6.1感知机简介:感知机是一个经典的二分类方法,由 Rosenblatt 于 1957 年时提出。它是神经网络和支持向量机的基础。感知机模型非常简单,输入为一些特征向量,输出则由正类和负类组成。而输入和输出之间,则是由符号函数连接。
6.6.2感知机的损失函数:是错误分类点到分离超平面之间的距离总和,其学习策略同样也是损失函数最小化。在scikit-learn 中,实现感知机通过调用
sklearn.linear_model.Perceptron()方法完成
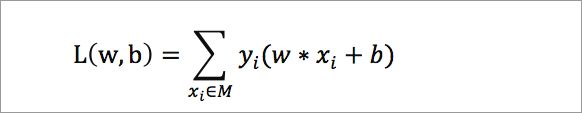
6.6.3使用感知机完成二分类任务
6.6.3.1在python命令行导入sklearn.datasets的make_classification模块,该模块提供的方法能生成一组被二分类的随机二维数组数据集
6.6.3.2其中:
-
n_features :特征个数
-
n_redundant:冗余信息,informative特征的随机线性组合
-
n_informative:多信息特征的个数
-
n_clusters_per_class :某一个类别是由几个cluster构成的
>>>from sklearn.datasets import make_classification
>>>X1,Y1=make_classification(n_features=2,n_redundant=0,n_informative=1, n_clusters_per_class=1) # 随机生成一组可以被二分类的数据
6.6.3.3先使用matplotlib将该数据集绘制出来,查看数据分布
>>>import matplotlib.pyplot as plt # 载入绘图模块
>>>plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) # 绘制数据集散点图
>>>plt.show() # 显示图
6.6.3.4关闭图形,回到python命令行
6.6.3.5使用感知机对数据集进行分类训练
>>>from sklearn.model_selection import train_test_split # 数据集分割模块
>>>from sklearn.linear_model import Perceptron # 感知机模块
>>>train_feature,test_feature,train_target,test_target=train_test_split(X1, Y1, train_size=0.7, random_state=88) # 将数据集划分为 70% 训练集和 30% 测试集
>>>model = Perceptron() # 建立感知机模型,使用默认参数
>>>model.fit(train_feature, train_target) # 使用训练集训练模型
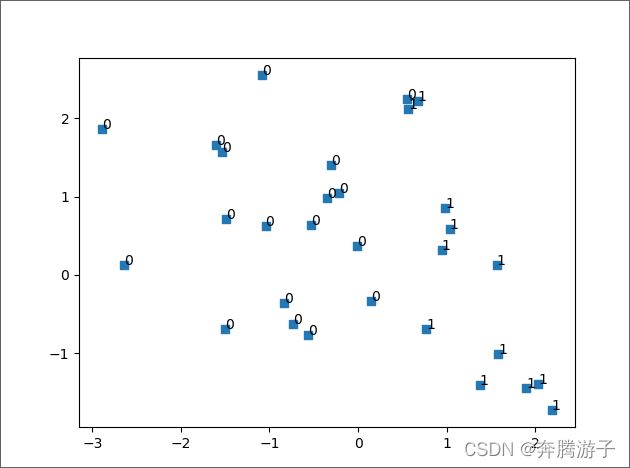
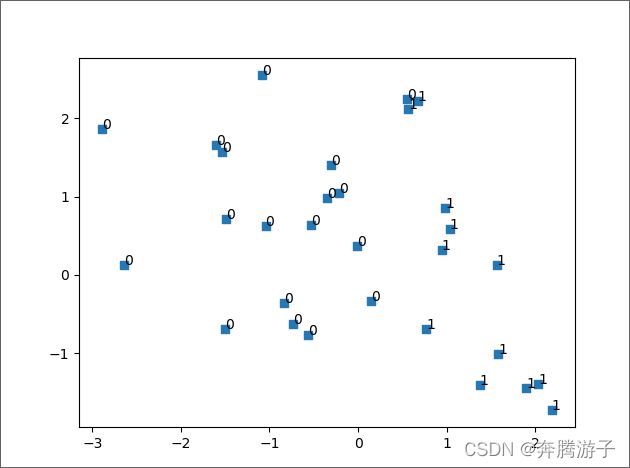
6.6.3.6训练结束后,使用测试数据集,进行预测,并使用matplotlib 可视化。
>>>results = model.predict(test_feature) # 使用测试集预测
>>>plt.scatter(test_feature[:, 0], test_feature[:, 1], marker=',') # 以方块样式绘制测试数据
# 将预测结果用标签样式标注在测试数据左上方
>>>for i, txt in enumerate(results):
… plt.annotate(txt, (test_feature[:, 0][i],test_feature[:, 1][i]))
…
>>>plt.show() # 显示图
6.6.3.7可以看到,通过感知机模型,我们完成了对数据集的二分类任务,但是由于数据集是随机的,所以每次得到的结果可能都不一样
6.6.3.8关闭图形,回到python命令行
6.7监督学习之支持向量机
6.7.1线性支持向量机
6.7.1.1感知机的学习过程由误分类驱动,即当感知机寻找到没有实例被错误分类时,就确定了分割超平面。这样虽然可以解决一些二分类问题,但是结果往往不是很合理,所以 Vapnik 于 1963 年提出了支持向量机理论,并将其用于解决线性分类问题。支持向量机也被看成是感知机的延伸。
6.7.1.2支持向量机就是通过找出一个最大间隔超平面来完成分类,从下图可以看到中间的实线就是我们找到的分割超平面,这里遵循的原则是分割超平面距离两条虚线距离间隔最大且一致。支持向量指的是两条虚线上的点

6.7.1.3使用scikit-learn完成实验
6.7.1.4使用exit()退出python命令行,再利用conda安装pandas模块,询问是否确定时输入y(若已安装则可以跳过此步骤)
>>>exit()
(zkbc)[zkpk@master ~]$ conda install pandas
6.7.1.5安装成功后利用python命令重新进入python命令行,并导入pandas模块,读取本地实验文件
(zkbc)[zkpk@master ~]$ python
>>>import pandas as pd
>>>df=pd.read_csv("/home/zkpk/experiment/spdlearn/two_class_data.csv",header=0)
6.7.1.6我们可以利用head方法查看前5行数据,了解数据结构,可以看到该数据有三列,分别是x、y和class,其中x和y是特征值,class是标签值用于区分类别,我们要做的就是根据测试数据的特征值,计算其标签值,查看分类准确度
>>>df.head()
6.7.1.7导入分割模块,将整个数据集划分为训练集和测试集两部分,其中训练集占 70%。
>>>from sklearn.model_selection import train_test_split # 导入数据集划分模块
# 读取特征值及目标值
>>>feature = df[["x", "y"]]
>>>target = df["class"]
# 对数据集进行分割
>>>train_feature,test_feature,train_target,test_target=train_test_split(feature, target, train_size=0.7,random_state=50)
6.7.1.8导入感知机和线性支持向量机分类器,利用fit方法训练模型
>>>from sklearn.svm import LinearSVC # 导入线性支持向量机分类器
>>>from sklearn.linear_model import Perceptron # 导入感知机分类器
>>>model = Perceptron() # 构建感知机预测模型
>>>model.fit(train_feature, train_target)
>>>model2 = LinearSVC() # 构建线性支持向量机分类模型
>>>model2.fit(train_feature, train_target)
6.7.1.9查看分类精准度(每次实验结果可能略有不同)
>>>model.score(test_feature,test_target) # 感知机分类准确度
>>>model2.score(test_feature,test_target) # 支持向量机分类准确度
6.7.1.10可以看到,支持向量机拥有比感知机更加准确的分类能力,当然,这里的数据集比较小,所以很难区分二者的分类能力,在实际生产中支持向量机的应用情景十分普遍
6.7.2非线性支持向量机
6.7.2.1非线性分类问题:实际生活中,我们大部分情况面对的却是非线性分类问题,因为实际数据往往都不会让你通过一个超平面就能完美分类。
6.7.2.2支持向量机引入了核函数来解决非线性分类的问题。通过核函数,我们可以将特征向量映射到高维空间中,然后再高维空间中找到最大间隔分割超平面完成分类。而映射到高维空间这一步骤也相当于将非线性分类问题转化为线性分类问题
6.7.2.3使用scikit-learn完成实验:
6.7.2.4导入实验相关模块,加载数据:通过 scikit-learn 来完成一个非线性分类实例。这次,我们选择了 digits 手写数字数据集。digits 数据集无需通过外部下载,可以直接由 scikit-learn 提供的datasets.load_digits() 方法导入。该数据集包含images部分,该部分存储的是1797张手写数字图片的影像,大小为8*8;data部分,该部分存储的是1797张图片灰度值转换的矩阵,每张图片像素已经转换成了64*1的矩阵;target部分,该部分存储的是每张图片的标签值,用于标识该图片是什么数字,默认有从0到9共10类
>>>from sklearn import datasets # 导入数据集模块
>>>import matplotlib.pyplot as plt # 导入绘图模块
>>>digits = datasets.load_digits() # 载入数据集
# 绘制数据集前 5 个手写数字的灰度图
>>>for index, image in enumerate(digits.images[:5]):
... plt.subplot(2, 5, index+1)
... plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
...
>>>plt.show()
6.7.2.5关闭图形,回到python命令行
6.7.2.6digits.images[1] 输出第 1 张手写数字对应的 8x8 矩阵。scikit-learn 已经将 8x8矩阵转换成了方便作为特征变量输入 64x1 的矩阵,并放在了 digits.data中。你可以使用digits.data[1]查看
>>>digits.data[1]
6.7.2.7划分训练集和测试集,然后针对测试集进行预测并评估预测精准度。
>>>from sklearn.svm import SVC #导入非线性支持向量机分类器
>>>from sklearn.metrics import accuracy_score # 导入评估模块
>>>from sklearn.model_selection import train_test_split #导入数据切分模块
>>>feature = digits.data # 指定特征值
>>>target = digits.target # 指定目标值
>>>train_feature,test_feature,train_target,test_target=train_test_split(feature, target, test_size=0.3,random_state=50) # 划分数据集,将其中 70% 划为训练集,另 30% 作为测试集
6.7.2.8建立非线性SVC模型,利用fit方法训练模型,再利用predict方法预测结果
>>>model = SVC() # 建立模型,使用默认参数
>>>model.fit(train_feature, train_target) # 模型训练
>>>results = model.predict(test_feature) # 模型预测
6.7.2.9利用sklearn中的统计评估模块,计算预测结果的准确率(每次结果可能略有不同)
>>>scores = accuracy_score(test_target, results) # 评估预测精准度
>>>scores #打印预测准确率
6.7.2.10可以看到上面的分类效果并不理想,这是为什么呢?因为在SVC超平面分类中,核函数将低维映射成高维是有一系列的参数,而在线性模型中很多参数的作用不大,但是在超平面分类中就需要我们理解一些参数并学会调参了,因为参数的内容很多,这里就不在赘述了,有兴趣的同学可以去查看SVC调参相关的资料
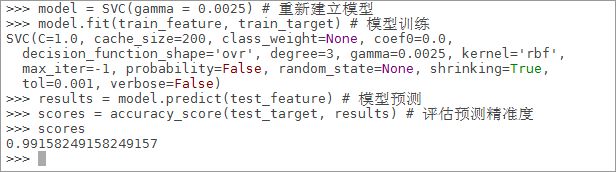
6.7.2.11通过调参提高模型的精度,调整SVC模型中的gamma值为“0.0025”,重新建立模型
>>>model = SVC(gamma = 0.0025) # 重新建立模型
>>>model.fit(train_feature, train_target) # 模型训练
>>>results = model.predict(test_feature) # 模型预测
>>>scores = accuracy_score(test_target, results) # 评估预测精准度
>>>scores
6.7.2.12通过尝试调整参数,可以看出模型的精准度有了很高的准确度(每次实验结果可能略有不同)
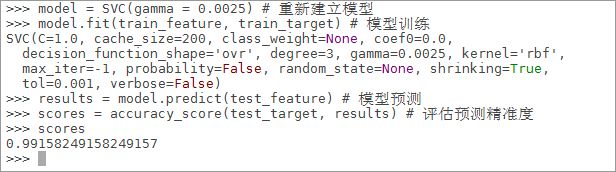
6.7.2.13可以看到调参之后的预测准确率达到了99%,这也告诉我了我们在非线性支持向量机中,理解并学会调参能够帮我们解决很多问题
7、总结
本节实验我们通过scikit-learn库学习了监督学习的相关知识,理解了监督学习的概念,学会了如何使用scikit-lean建立回归和分类模型,了解了各分类模型在实际应用中的优劣,最重要的是要理解模型的参数,学会调参数可以使得模型获得更高的性能,调参部分的内容还需要多学习多理解。