Python实现一元回归多元回归及参数检验

---

#pic_center =400x
系列文章：

---

---

一元回归

人工实现代码

# 一元线性回归
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

x = np.array([100, 110, 120, 130, 140, 150, 160, 170, 180, 190])
y = np.array([45, 51, 54, 61, 66, 70, 74, 78, 85, 89])



a, b = 0,0;
def fitted_line(x):
    return a*x+b

def linear_regression(x, y, cl=0.9):
    """
    linear regression函数y = ax + b
    cl为置信水平
    alpha为显著性水平
    """
    data = pd.DataFrame({'x': x, 'y': y}).sort_values(by='x')
    x = np.asarray(data['x'])
    y = np.asarray(data['y'])

    alpha = 1 - cl
    print('置信水平: {}% C.L.\n'.format(100 * cl))
    print('显著性水平alpha: {}\n'.format(alpha))

    a, b = np.polyfit(x, y, deg=1)

    print('斜率: {}\n'.format(a))

    print('截距: {}\n'.format(b))

    Sxx = np.sum((x - np.mean(x)) ** 2)
    Syy = np.sum((y - np.mean(y)) ** 2)
    Sxy = np.sum((x - np.mean(x)) * (y - np.mean(y)))

    dof = len(x) - 2
    print('自由度: {}\n'.format(dof))

    sigma = np.sqrt((Syy - a * Sxy) / dof)
    print('sigma的无偏估计: {}\n'.format(sigma))

    R_sq = a * Sxy / Syy
    print('拟合优度R² : {}\n'.format(R_sq))

    t_value = stats.t.isf(alpha / 2, dof)
    print('t值: {}\n'.format(t_value))

    if np.abs(a) / sigma * np.sqrt(Sxx) >= t_value:
        print('t检验: 线性回归效果显著\n')
    else:
        print('t检验: 线性回归效果不显著\n')

    print('斜率的置信区间: {}% C.L.\n[{}, {}]\n'.format(
        100 * cl,
        a - t_value * sigma / np.sqrt(Sxx),
        a + t_value * sigma / np.sqrt(Sxx)))

    print('截距的置信区间: {}% C.L.\n[{}, {}]\n'.format(
        100 * cl,
        b - t_value * sigma * np.sqrt(1. / len(x) + np.mean(x) ** 2 / Sxx),
        b + t_value * sigma * np.sqrt(1. / len(x) + np.mean(x) ** 2 / Sxx)))

    print('回归函数的函数值的点估计和置信区间: {}% C.L.\n下区间端点: {}\n上区间端点: {}\n'.format(100 * cl,
                                                                       fitted_line(x) - t_value * sigma * np.sqrt(
                                                                           1. / len(x) + (x - np.mean(x)) ** 2 / Sxx),
                                                                       fitted_line(x) + t_value * sigma * np.sqrt(
                                                                           1. / len(x) + (x - np.mean(x)) ** 2 / Sxx)))

    print('观测值的点预测和预测区间: {}% C.L.\n下区间端点: {}\n上区间端点: {}\n'.format(100 * cl,
                                                                  fitted_line(x) - t_value * sigma * np.sqrt(
                                                                      1. + 1. / len(x) + (x - np.mean(x)) ** 2 / Sxx),
                                                                  fitted_line(x) + t_value * sigma * np.sqrt(
                                                                      1. + 1. / len(x) + (x - np.mean(x)) ** 2 / Sxx)))

    fig = plt.figure()
    ax = fig.add_subplot()
    ax.scatter(x, y, s=1, c='k', )
    ax.plot(x, fitted_line(x), lw=1, label='Linear regression')
    ax.fill_between(x,
                    fitted_line(x) - t_value * sigma * np.sqrt(1. / len(x) + (x - np.mean(x)) ** 2 / Sxx),
                    fitted_line(x) + t_value * sigma * np.sqrt(1. / len(x) + (x - np.mean(x)) ** 2 / Sxx),
                    alpha=0.3,
                    label=r'Confidence limit'.format(100 * cl))
    ax.set_xlabel('$x$')
    ax.set_ylabel('$y$')
    ax.legend()
    fig.savefig('Linear regression.png', dpi=300)

linear_regression(x,y)

Python实现一元线性回归

statsmodels实现

import csv
import sys

import matplotlib.pyplot as  plt
import numpy
import numpy as np
import statsmodels.api as  sm
import xlrd
import openpyxl
import xlsxwriter
# xlrd读取表格数据，支持xlsx和xls格式的excel表格；xlwt写入excel表格数据

file_path = "E:\\code\\experiment\\data\\singleRegression\\source\\userId\\testId\\source.xlsx"
target_path = "E:\\code\\experiment\\data\\singleRegression\\result\\userId\\testId"
variable = "自变量"
dep_variable = "因变量"

# Matplotlib 默认情况不支持中文，我们可以使用以下简单的方法来解决：
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def get_excel_data_all(file_path):
    data_excel = xlrd.open_workbook(file_path)
    table = data_excel.sheets()[0]  # 通过索引顺序获取sheet
    row_count= table.nrows  # 获取该sheet中的有效行数
    col_count = table.ncols  # 获取该sheet中的有效列数
    result= []
    for i in range(row_count):
        result.append(table.row_values(i, start_colx=0, end_colx=None))
    row_data = table.row_values(0, start_colx=0, end_colx=None)
    return row_count, col_count, result

if __name__ == '__main__':
    for i in range(0, len(sys.argv)):
        pass
        # print(i,"---" , sys.argv[i])
    if len(sys.argv)>1:
        file_path = sys.argv[1]
        if len(sys.argv) > 2:
            target_path = sys.argv[2]
            if len(sys.argv)>4:
                variable = sys.argv[3]
                dep_variable = sys.argv[4]
    row_count, col_count, result = get_excel_data_all(file_path)
    # 一元回归只能有1个变量
    if col_count > 2:
        col_count = 2
    heads = result[0]
    result = numpy.array(result)
    x_data = []
    y_data = []
    for i in range(1, row_count):
        for j in range(0, col_count - 1):
            x_data.append(float(result[i][j]))
        y_data.append(float(result[i][col_count - 1]))

    model = sm.OLS( y_data,x_data)
    res = model.fit()
    beta = res.params
    print(res.params)  # # 取系数
    summary = res.summary()
    print(res.summary())  # # 回归 分析摘要
    with open(target_path+"\\result.txt",
              "w",encoding="utf-8") as f:
        f.write(str(summary))
    Y = res.fittedvalues  # 预测值
    # 原始数据
    plt.scatter(x_data,y_data, marker = "o", s = 5,  cmap="viridis", alpha=0.3, label="原数据")
    # 预测数据
    plt.plot(x_data, Y, 'r--.', label='预测数据')
    plt.legend(loc='upper left')  # 图例，显示labe
    plt.xlabel(variable)
    plt.ylabel(dep_variable);
    plt.savefig(target_path+'\\result.png' )

    # with open("E:\\code\\experiment\\back\\formal\\data\\data_result\\single_regression\\x.csv",
    #           "a",encoding="utf-8") as f:
    #     writer = csv.writer(f)
        # writer.writerow(row)
        # f.write(pic_target_path+'\\2.png')

    # plt.plot(x_data,Y,color="r", linestyle="solid",linewidth=2,marker="o")
    plt.show()

sklearn.linear_model

import csv
import sys
import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

from sklearn.metrics import r2_score

import statsmodels.api as sm

# xlrd读取表格数据，支持xlsx和xls格式的excel表格；xlwt写入excel表格数据

file_path = "E:\\code\\experiment\\data\\singleRegression\\source\\userId\\testId\\source.xlsx"
target_path = "E:\\code\\experiment\\data\\singleRegression\\result\\userId\\testId"
variable = "年龄"
dep_variable = "身高"

# Matplotlib 默认情况不支持中文，我们可以使用以下简单的方法来解决：
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


if __name__ == '__main__':
    for i in range(0, len(sys.argv)):
        pass
        # print(i,"---" , sys.argv[i])
    if len(sys.argv)>1:
        file_path = sys.argv[1]
        if len(sys.argv) > 2:
            target_path = sys.argv[2]
            if len(sys.argv)>4:
                variable = sys.argv[3]
                dep_variable = sys.argv[4]


    data = pd.read_excel(file_path)
    # 查看数据时，输入：
    # print(data.head())
    # plt.figure(figsize=(16, 8))
    x_data = data[['年龄']]
    y_data = data[['身高']]
    # “未命名：0”列是多余的。所以，我们把这一列删除。
    # data.drop(['Unnamed: 0'], axis=1)
    # plt.scatter(data.loc[:, variable], data.loc[:, dep_variable])

    # 画出散点图，求x和y的相关系数
    model = LinearRegression()
    res =  model.fit(x_data,y_data)
    # 预测数据
    predictions = model.predict(x_data)
    # 原始数据
    plt.scatter(x_data, y_data, marker="o",   label="原数据")

    plt.plot(x_data, predictions, 'r--.',linewidth=3, label='预测数据')
    plt.title("Y = {:.5} + {:.5}X".format(model.intercept_[0], model.coef_[0][0]))
    # plt.show()
    plt.legend(loc='upper left')  # 图例，显示labe
    plt.xlabel(variable)
    plt.ylabel(dep_variable)

    plt.savefig(target_path + '\\result.png')

    print("The linear model is: Y = {:.5} + {:.5}X".format(model.intercept_[0], model.coef_[0][0]))


    x2 = sm.add_constant(x_data)
    est = sm.OLS(y_data,x2).fit()
    summary = est.summary()
    print(est.summary())

    with open(target_path+"\\result.txt",
              "w",encoding="utf-8") as f:
        f.write(str("The linear model is: Y = {:.5} + {:.5}X".format(model.intercept_[0], model.coef_[0][0])))
        f.write("\n")
        f.write("==============================================================================\n")
        f.write(str(summary))

    plt.show()

报告注解

            content.append(Graphs.draw_text('Dep. Variable: 响应变量的名称， Dep为Depended的缩写'
                                        'Model/Method: 表示这里使用了普通最小二乘法OLS'
                                        'Date/Time: 对模型进行估计的日期和时间'
                                        'No. Observations: 样本容量'
                                        'Df Residuals: 样本容量减去参与估计的参数个数'
                                        'Df Model:用到的解释变量的个数(不是参数个数)'
                                        'Covariance Type:协方差类型，默认为nonrobust'
                                        'R-squared/Adj. R-squared: 决定系数与修订系数'
                                        'F-statistic/Prob (F-statistic):方差分析结果'
                                        'Log-Likelihood:最大似然对数'
                                        'AIC:赤池信息准则'
                                        'BIC:贝叶斯信息准则，属于信息准则的一种'))
            content.append(Graphs.draw_text('R-squared和Adj.R-squared的取值范围为0～1，它们的值越接近1，则模型的拟合程度越高；'))

一元线性回归及案例（Python）
一文教你全面掌握用Python实现线性回归

数据读取

无表头，列名 .csv格式

value_array = np.genfromtxt("./datasets/test.csv", delimiter=',')
print(value_array)
x = value_array[0]
y = value_array[1]
print(x)
print(type(x))
print(y)

python数据分析：一元线性回归

panda读取csv

from pandas import read_csv
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
data = read_csv('data.csv',encoding='gbk')
#画出散点图，求x和y的相关系数
plt.scatter(data.loc[:,'广告投入'], data.loc[:,'销售额'])
Model = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]

.csv文件数据直接读取为numpy array
Python读取csv文件，并加载其中的几行几列

python去读csv文件，以及numpy的ndarray与pandas的series和dataframe之间互转

panda读取excel

    data = pd.read_excel(file_path)
    # 画出散点图，求x和y的相关系数
    plt.scatter(data.loc[:, '年龄'], data.loc[:, '身高'])
    x_data = data[['年龄']]
    y_data = data[['身高']]

panda多元回归

import csv
import math
import sys
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
import statsmodels.api as sm
# xlrd读取表格数据，支持xlsx和xls格式的excel表格；xlwt写入excel表格数据
file_path = "C:\\Users\\ytm\\Desktop\\test.xlsx"
target_path = "C:\\Users\\ytm\\Desktop\\result\\multi"
variable = ["id","age","number"]
dep_variable = "score"

# Matplotlib 默认情况不支持中文，我们可以使用以下简单的方法来解决：
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 0 program
# 1 fileCompleteFileName
# 2   targetDir
# 3-  variable
# -1  depVariable

if __name__ == '__main__':
    args_len =  len(sys.argv)
    for i in range(0, args_len):
        print(i,"---" , sys.argv[i])
    if args_len > 1:
        file_path = sys.argv[1]
        if args_len > 2:
            target_path = sys.argv[2]
            dep_variable = sys.argv[-1]
            variable = []
            for j in range(3, args_len-1):
                variable.append(sys.argv[j])


    data = pd.read_excel(file_path)

    x_data = data[[i for i in variable]]


    y_data = data[[dep_variable]]
    x = np.column_stack(x_data)

    model = LinearRegression()
    res =  model.fit(x_data,y_data)

    resultForm = "The linear model is: Y = {:.5} ".format(model.intercept_[0])
    for i  in  range(0,len(variable)):
        resultForm += "+ ({:.5}*".format(model.coef_[0][i])+variable[i] + ")  "
    resultForm += "\n\n\n"


    # 评估模型

    X2 = sm.add_constant(x_data)
    est = sm.OLS(y_data,X2)
    est2 = est.fit()
    summary = est2.summary();
    print(est2.summary())
    with open(target_path+"\\result.csv",
              "w",encoding="utf-8") as f:
        for i in range(0, len(variable)):
            resultForm += "+ ({:.5}*".format(model.coef_[0][i]) + variable[i] + ")  "
        resultForm += "\n\n\n"
        f.write(resultForm)
        f.write("==============================================================================\n")
        f.write(str(summary))


    # mpl.rcParams['legend.fontsize'] = 10


    x_data = [ x_data[i].values for i in variable]
    y_data = y_data[dep_variable].values

    min_x = np.array([ x_data[i].min() for i in range(0,len(variable))])
    max_x = np.array([x_data[i].max() for i in range(0, len(variable))])
    step_x = (max_x - min_x+1)/5
    min_y = y_data.min()
    max_y = y_data.max()
    step_y = math.ceil((max_y-min_y+1)/5)


    for i in range(0,len(variable)):
        for j in range(i+1, len(variable)):
            fig = plt.figure()
            ax = fig.add_subplot(projection='3d')
            # 坐标轴标签重叠
            plt.tight_layout()
            ax.scatter(x_data[i], x_data[j], y_data)
            ax.set_xticks(np.arange(min_x[i], max_x[i]+step_x[i], math.ceil(step_x[i])))
            ax.set_xlabel("x:"+variable[i])
            ax.set_yticks(np.arange(min_x[j], max_x[j]+step_x[j], math.ceil(step_x[j])))

            ax.set_ylabel("y:"+variable[j])
            # ax.set_yticks([np.linspace(minx-1, maxx+1, (maxx-minx + 1)/10)])
            print("y:"+variable[j])
            ax.set_zticks(np.arange(min_y, max_y+step_y, step_y))
            ax.set_zlabel("z:"+dep_variable)
            plt.savefig(target_path+"\\result-"+str(i)+"-"+ str(j)+".png")

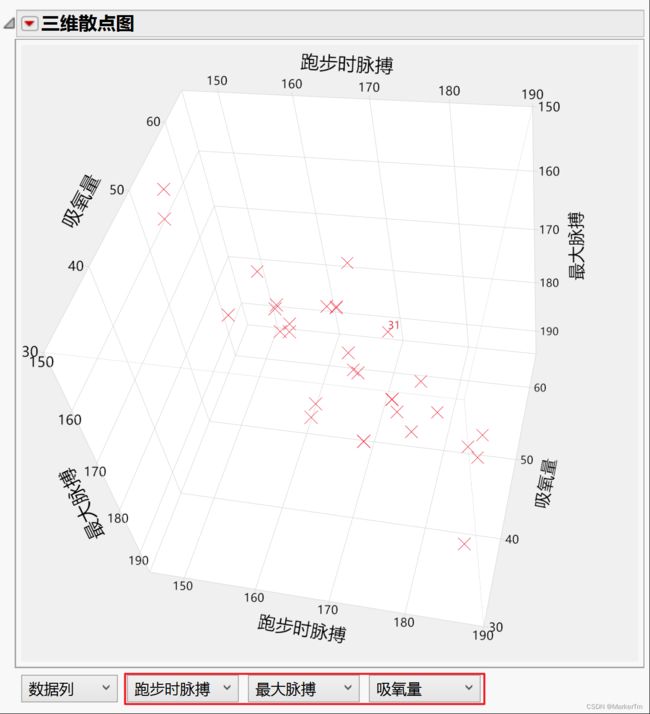
JMP借鉴

多元回归

statsmodel官方

python statsmodel 回归结果提取（R方 T值 P-value)

JMP借鉴

Scipy 显著性检验

多元线性回归模型可视化