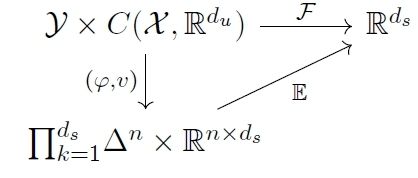前言
之前的系列里提到Attention机制在算子学习中的应用前景,今年的机器学习顶刊JMLR就发表了一篇相关的论文,利用Attention机制对时空耦合数据进行耦合,实现了超分辨率的插值方法,在各种各样的复杂场景下有广泛利用,为算子学习理论提供了坚实的基础。
Kissas, Georgios, et al. "Learning operators with coupled attention." Journal of Machine Learning Research 23.215 (2022): 1-63.
最开始还是要介绍一下算子学习的目标,本质是学习两个无穷维空间之间的映射,这里的映射和一般所说的ODE的区别就是函数控制的自由度是无穷的。DeepONet的作者已经证明了利用神经网络去学习这种类型的映射是可行,并给出了一种最原始的网络设计,但是网络架构的潜力并没有得到充分的发掘,大多数的结果还是基于严格理论分析,这篇也是。但是这篇论文的Attention机制是让人疑惑的,它与Transformer中的这个机制是不同,这个是做了空间维度上的插值,相当于是超分辨率方法,可以视作是计算机图形学的一个分支。
简而言之,就是在两个无穷维空间中的映射,由于无法得到解析解,我们一般都是在两个无穷维空间中采样有限个样本然后离散近似求解,这篇文章的思路也是如此,就是对于只有有限个已知的输入函数,可以通过学习到对任意插入未知的值的映射。这篇文章能够发表在JMLR说明其是非常理论的,下面就尽可能简化理论分析,给出该方法的一些思路。
理论结果
首先我们从理论的角度分析这篇文章,给定\( \mathcal{X} \subset \mathbb{R} ^{d_x} \)和\(\mathcal{Y} \subset \mathbb{R} ^{d_y}\),将\( x\in \mathcal{X} \)称为输入位置,\(y\in \mathcal{Y} \)称为查询位置。将定位为\( C\left( \mathcal{X} ,\mathbb{R} ^{d_u} \right) \)和\(C\left( \mathcal{Y} ,\mathbb{R} ^{d_s} \right)\)定义为\( \mathcal{X} \rightarrow \mathbb{R} ^{d_u} \)和\(\mathcal{Y} \rightarrow \mathbb{R} ^{d_s}\)的连续函数空间。给定任意真实数据对\( \left[u^l\left(x\right), s^l\left(y \right)\right] \),算子学习的目标是学习一个算子\(\mathcal{F}: C\left(\mathcal{X}, \mathbb{R}^{d_u}\right) \rightarrow C\left(\mathcal{Y}, \mathbb{R}^{d_s}\right)\)使得
$$ \mathcal{F}\left(u^{\ell}\right)=s^{\ell} $$
定理一:给定一类通用算子\(\mathcal{A} \ni \mathcal{F}: C\left(\mathcal{X}, \mathbb{R}^{d_u}\right) \rightarrow C\left(\mathcal{Y}, \mathbb{R}^{d_s}\right) \),对于任意的连续算子\(\mathcal{G}: C\left(\mathcal{X}, \mathbb{R}^{d_u}\right) \rightarrow C\left(\mathcal{Y}, \mathbb{R}^{d_s}\right) \)和\( \epsilon>0 \),存在一个\( \mathcal{F} \in \mathcal{A} \)使得
$$ \mathop {\mathrm{sup}} \limits_{u\in \mathcal{U}}\mathop {\mathrm{sup}} \limits_{y\in \mathcal{Y}}\parallel \mathcal{G} (u)(y)-\mathcal{F} (u)(y)\parallel _{\mathbb{R} ^{d_s}}^{2}<\epsilon $$
其中
$$ \mathcal{F}(u)(y)=\sum_{i=1}^n g_i(y) \odot v_i(u) $$
定理二:对于任意的连续算子\(\mathcal{G}: C\left(\mathcal{X}, \mathbb{R}^{d_u}\right) \rightarrow C\left(\mathcal{Y}, \mathbb{R}^{d_s}\right) \)和\( \epsilon>0 \),存在函数 \(v(u)\)和 \(\varphi(y)\)使得
$$ \sup _{u \in \mathcal{U}} \sup _{y \in \mathcal{Y}}\left\|\mathcal{G}(u)(y)-\mathbb{E}_{\varphi(y)}[v(u)]\right\|_{\mathbb{R}^{d_s}}^2<\epsilon $$
谱系化编码保留了普遍性:令\(D_d:U \rightarrow \mathbb{R} ^d\)代表基\( \left{ e_1,...,e_d \right}\)上的投影。那么对于任何连续函数 \(h:\mathcal{U} \rightarrow \mathbb{R} ^n\)以及任何>0,存在\( d \)和\(f\in A_N\)使得
$$ \sup _{u \in \mathcal{U}}\left\|h(u)-f \circ \mathcal{D}_d(u)\right\|<\epsilon $$
方法与网络架构
根据定理二,attention机制就是求解序列对序列任务,也就是将有限长度输入\( \left( u_1,...,u_{T_u} \right) \)映射到特征序列\(\left( v_1,...,v_{T_u} \right)\),随后根据插入位置,产生一个概率分布序列\(\left( \varphi _{i1},...,\varphi _{iT_u} \right)\),使得
$$ \varphi _{ij}\ge 0,\quad \sum_{j=1}^{T_u}{\varphi _{ij}}=1. $$
该点的特征为
$$ c_i=\sum_{j=1}^{T_u}{\varphi _{ij}}v_j. $$
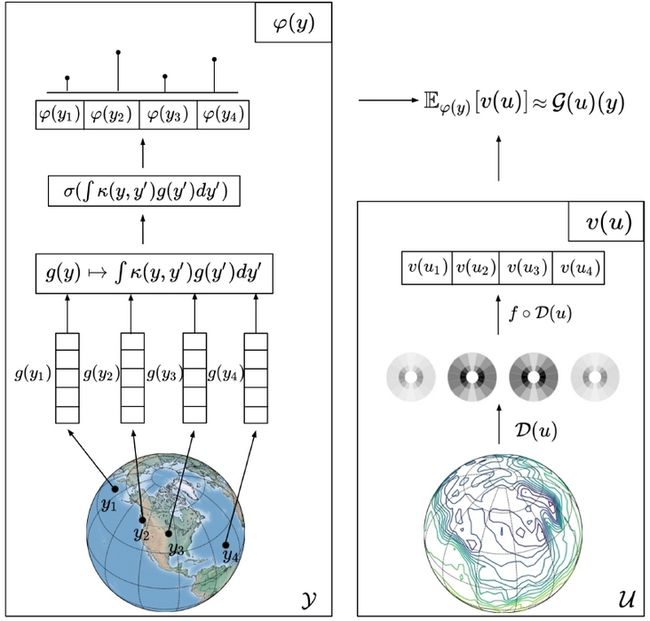
根据定理二,我们将应用attention机制来学习函数空间之间的运算符,方法是将一个输入函数\( u \)映射到一组有限的特征\( v(u)\in \mathbb{R} ^{n\times d_s} \),并在这些特征分布\(\varphi (y)\)上取一个平均数,对于任意的查询位置\( y\in \mathcal{Y} \)
$$ \mathcal{F} (u)(y):=\mathbb{E} _{\varphi (y)}[v(u)] $$
具体而言,模型的具体原型就是
$$ \mathcal{F}(u)(y)=\mathbb{E}_{\varphi(y)}[v(u)]=\sum_{i=1}^n \sigma\left(\int_{\mathcal{Y}} \kappa\left(y, y^{\prime}\right) g\left(y^{\prime}\right) d y^{\prime}\right)_i \odot v_i(u) $$
其中
$$ \kappa\left(y, y^{\prime}\right):=\frac{k\left(q_\theta(y), q_\theta\left(y^{\prime}\right)\right)}{\left(\int_{\mathcal{Y}} k\left(q_\theta(y), q_\theta(z)\right) d z\right)^{1 / 2}\left(\int_{\mathcal{Y}} k\left(q_\theta\left(y^{\prime}\right), q_\theta(z)\right) d z\right)^{1 / 2}},\\ \sigma: \mathbb{R}^n \rightarrow \Delta^n,\\ \quad g \mapsto\left(\frac{\exp \left(g_1\right)}{\sum_{i=1}^n \exp \left(g_i\right)}, \quad \cdots \quad, \frac{\exp \left(g_n\right)}{\sum_{i=1}^n \exp \left(g_i\right)}\right)^{\top} $$
最后对输入函数做特征编码,也即
$$ \mathcal{D}: C\left(\mathcal{X}, \mathbb{R}^{d_u}\right) \rightarrow \mathbb{R}^d $$
文章里是使用了全连接神经网络完成这项任务。
下面说一些模型细节方便理解:
积分核的逼近:积分核是连续,这在现实中是不可实现的,可以用Monte-Carlo估计器来近似计算
$$ \int_{\mathcal{Y}} \kappa\left(y, y^{\prime}\right) g\left(y^{\prime}\right) \approx \frac{\operatorname{vol}(\mathcal{Y})}{P} \sum_{i=1}^P \kappa\left(y, y_i\right) g\left(y_i\right) $$
当目标域是\( \mathcal{Y}\)是低维的时候,如在许多物理问题中,Gauss-Legendre正交规则可以提供一个准确而有效的方法来替代Monte-Carlo近似法。使用Q Gauss-Legendre结点和权重,我们可以将所需的积分逼近为
$$ \int_{\mathcal{Y}} \kappa\left(y, y^{\prime}\right) g\left(y^{\prime}\right) d y^{\prime} \approx \sum_{i=1}^Q w_i \kappa\left(y, y_i^{\prime}\right) g\left(y_i^{\prime}\right) $$
此外,作者还是用了位置编码对查询位置进行了编码,使用小波散射网络对\( u \)进行特征编码,具体细节可以参考论文。
损失函数:
$$ \mathcal{L}(\theta)=\frac{1}{N} \sum_{i=1}^N \sum_{\ell=1}^P\left(s^i\left(y_{\ell}^i\right)-\mathcal{F}_\theta\left(u^i\right)\left(y_{\ell}^i\right)\right)^2 $$
使用梯度下降进行参数优化。
实验结果
作者将其方法和FNO以及DeepOnet进行了比较,主要针对
- Antiderivative
- Darcy Flow
- Mechanical MNIST
- Shallow Water Equations
- Climate modeling
这五个场景进行了比较,均取得了不错的效果,具体可以参考文章。
结论
这篇文章Attention的思路和DeepOnet是相似,都是对传统的万能逼近定理进行了推广了,使之能够对无穷维空间之间的映射进行处理并提供了严格理论分析,这些贡献是不言而喻。应用神经网络对传统的算子求解器进行加速已经成了大趋势,有兴趣的读者可以将之与GNN结合在一起去处理。
如果图网络和attention机制在算子学习中的应用感兴趣,推荐继续阅读以下的论文:
Pfaff, T., Fortunato, M., Sanchez-Gonzalez, A., & Battaglia, P. W. (2020). Learning mesh-based simulation with graph networks. arXiv preprint arXiv:2010.03409.
Han, X., Gao, H., Pffaf, T., Wang, J. X., & Liu, L. P. (2022). Predicting Physics in Mesh-reduced Space with Temporal Attention. arXiv preprint arXiv:2201.09113.