【刷题日记】BFS 经典题目
大家好,我是白晨,一个不是很能熬夜,但是也想日更的人✈。如果喜欢这篇文章,点个赞,关注一下白晨吧!你的支持就是我最大的动力!
文章目录
- 前言
- BFS 经典题目
-
- 1. N 叉树的层序遍历
- 2. 腐烂的橘子
- 3. 单词接龙
- 4. 最小基因变化
- 5. 打开转盘锁
- 后记
前言
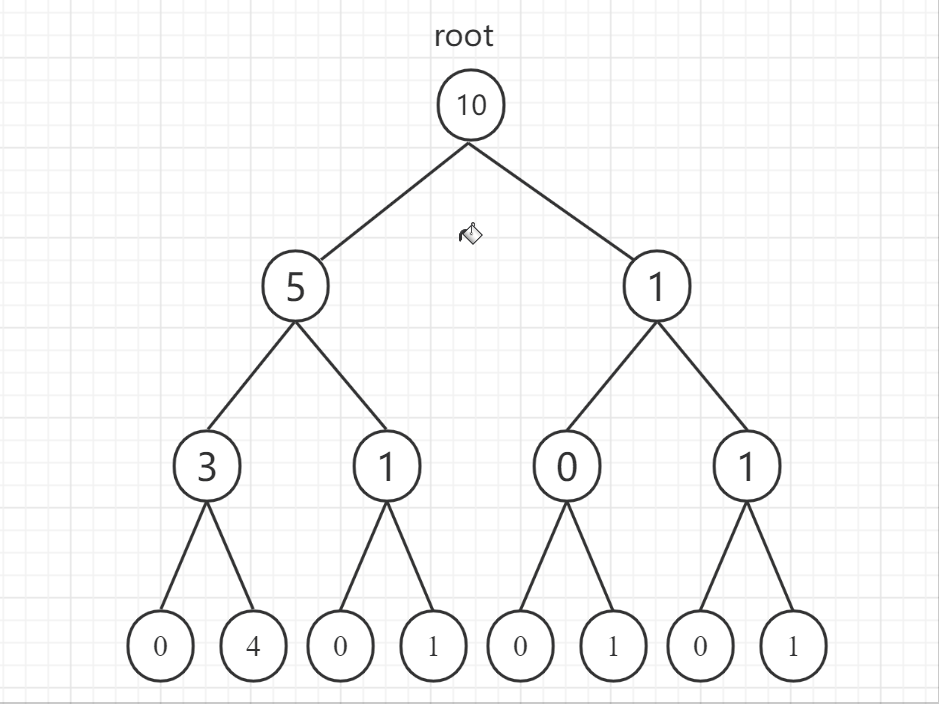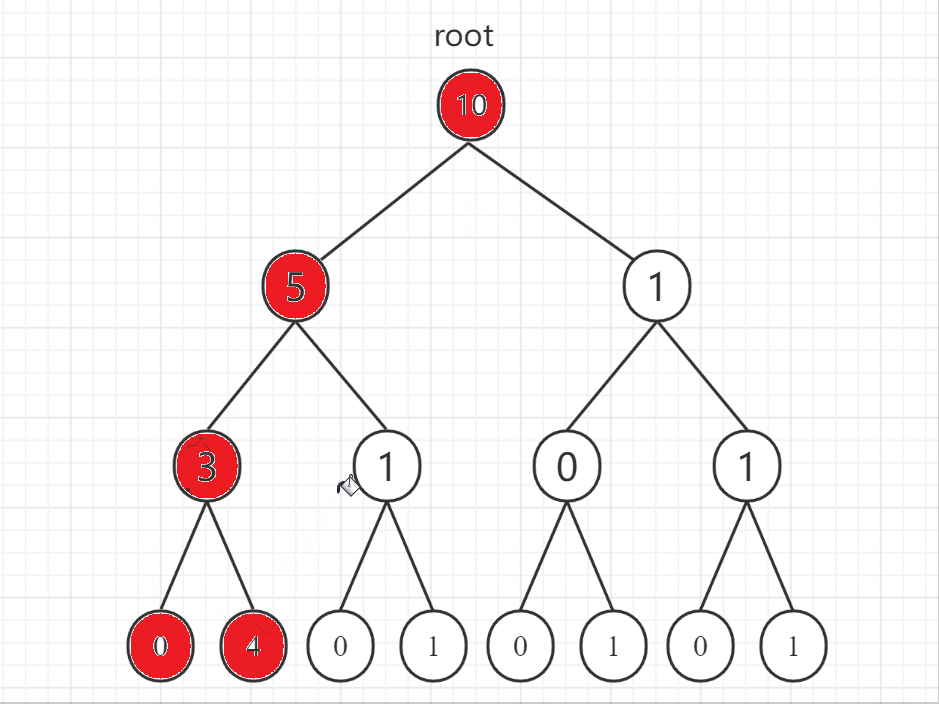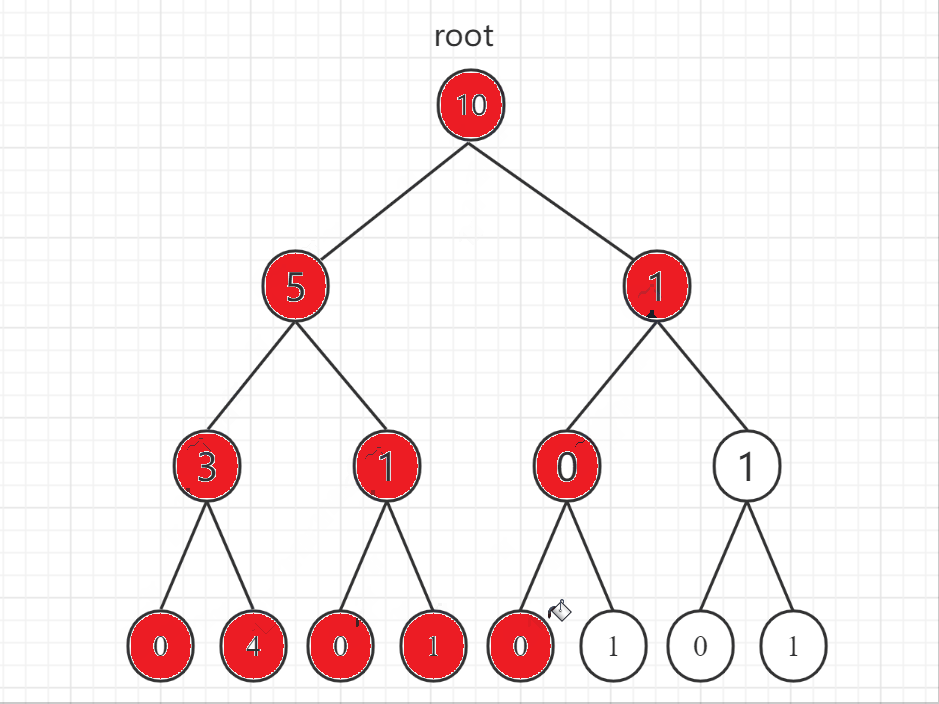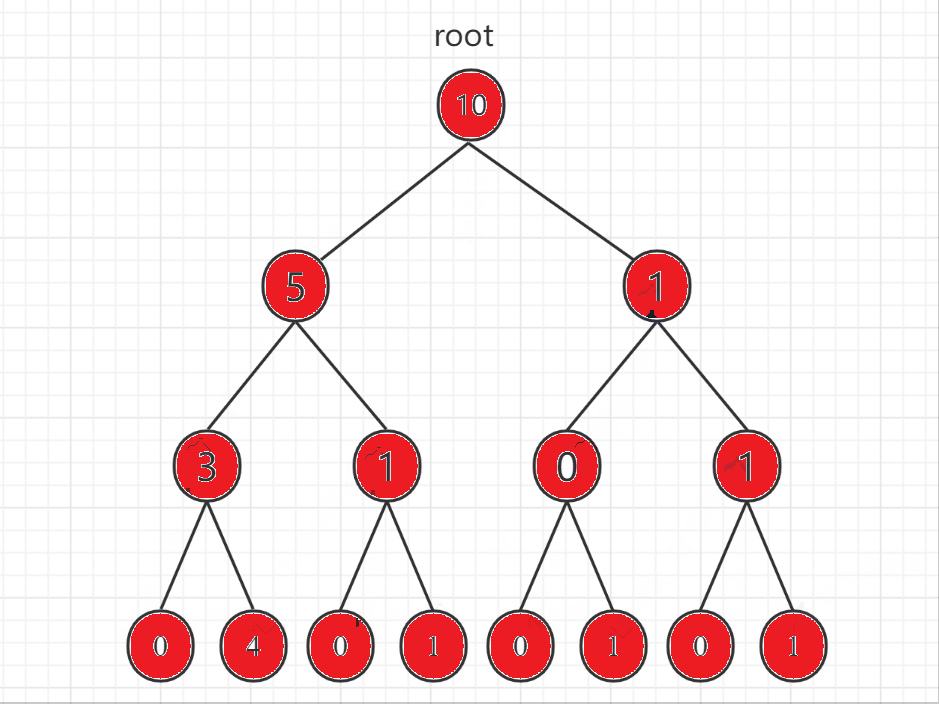
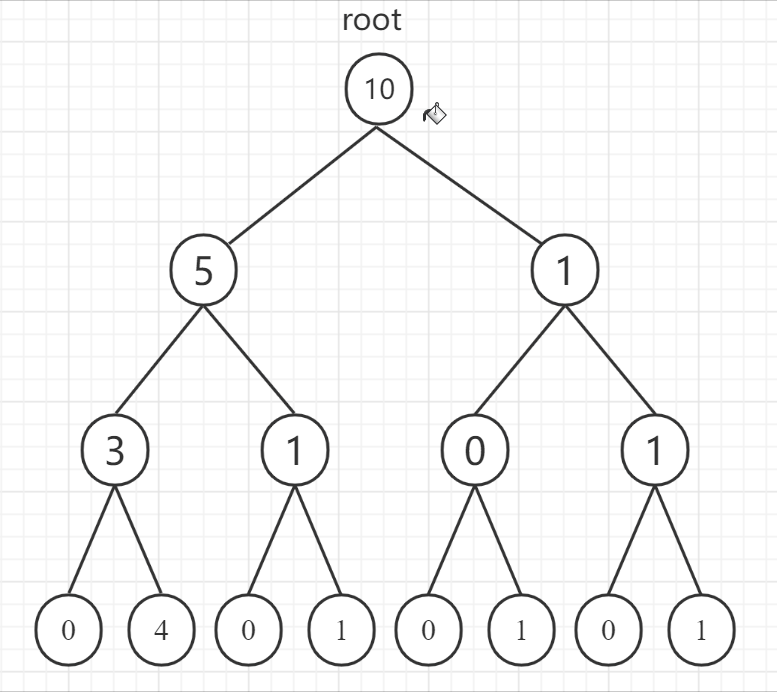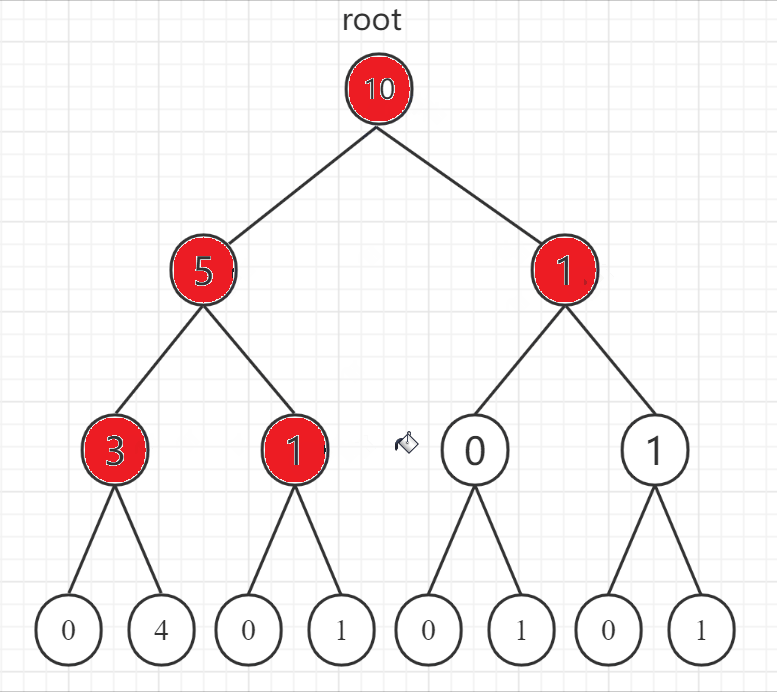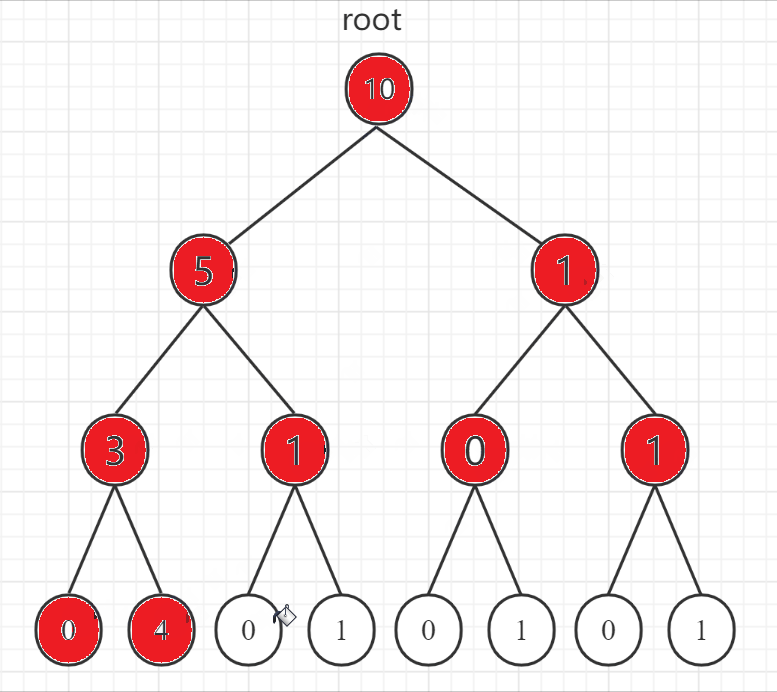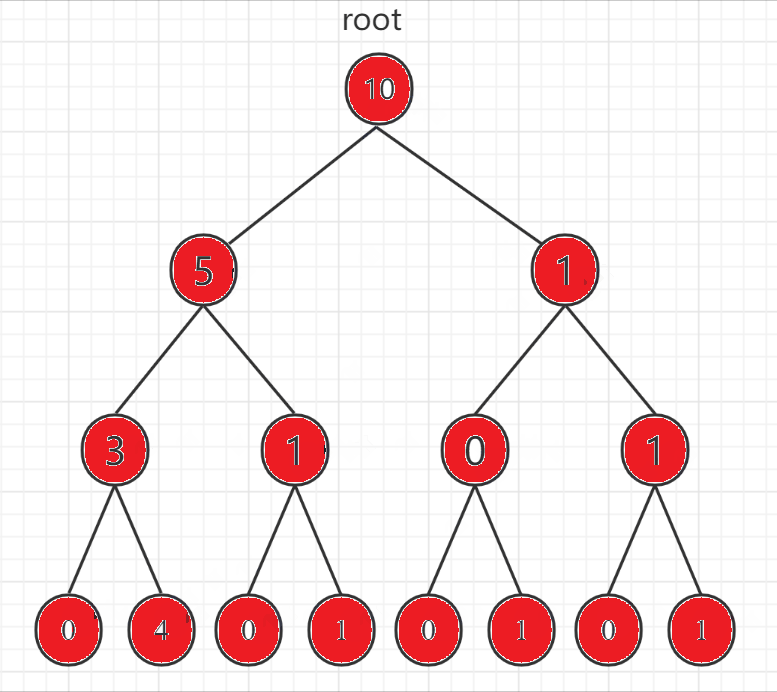
广度优先搜索(Breadth First Search)简称广搜或者 BFS,概念相对于深度优先搜索。下面用二叉树的遍历展示一下深度优先搜索和广度优先搜索的区别:
- 深度优先搜索
- 广度优先搜索
可以看到深度优先搜索和广度优先搜索在二叉树的遍历上分别体现为前序遍历和层序遍历。
- 广度优先搜索的思路
- 首先,将开始遍历的结点加入队列,遍历这个结点后,将其孩子结点入队。
- 接着,按照队列的顺序将结点出队,遍历并将其孩子结点入队。
- 重复2过程,直到队列为空。
- 广度优先搜索的优势
- 没有过多的堆栈消耗,耗时少。
- 在求最大或者最小问题时比较好用。
BFS 经典题目
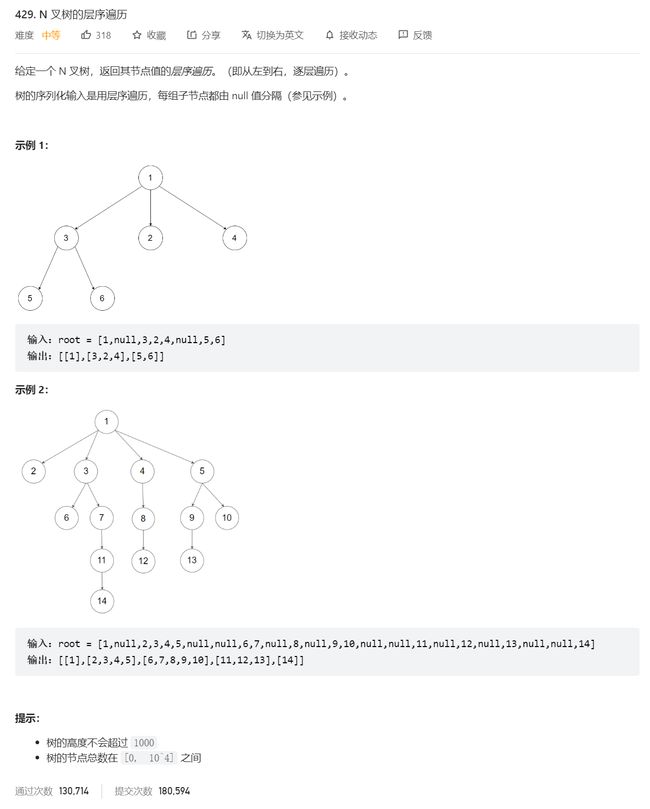
1. N 叉树的层序遍历
原题链接:N 叉树的层序遍历
算法思想:
- 首先,将开始遍历的结点加入队列,遍历这个结点后,将其孩子结点入队。
- 接着,按照队列的顺序将结点出队,遍历并将其孩子结点入队。
- 重复2过程,直到队列为空。
代码实现:
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
// 广度优先搜索使用的队列
queue<Node*> q;
// 根节点不为空才入队
if(root != nullptr)
q.push(root);
// 存放每层结点数据的数组
vector<vector<int>> vv;
// 队列为空才停止搜索
while(!q.empty())
{
// 记录每层的结点个数
size_t s = q.size();
// 记录每层的结点数据
vector<int> v;
// 将这层的结点遍历
while(s--)
{
Node* pnode = q.front();
q.pop();
v.push_back(pnode->val);
// 将其孩子入队
for(auto& child : pnode->children)
{
if(child)
q.push(child);
}
}
// 记录这一层的结点数据
vv.push_back(v);
}
return vv;
}
};
2. 腐烂的橘子
原题链接:腐烂的橘子
算法思想:
-
由于题目要求是返回最小完全腐烂的时间,所以,用深度优先搜索很不好做,并且这道题的腐烂传染方式很适合BFS。
-
首先,将开始腐烂的橘子坐标加入队列,遍历这个橘子后,将其上、下、左、右四个方向的橘子入队(下一轮腐烂的橘子)。
-
接着,按照队列的顺序将橘子出队,遍历并将其上、下、左、右四个方向的橘子结点入队。
-
将一轮腐烂的橘子遍历完后,计时+1分钟。
-
重复2、3过程,直到队列为空。
-
最后,检查是否有新鲜橘子,如果有,返回-1,没有,返回分钟数。
-
代码实现:
class Solution {
public:
int nextMove[4][2] = {{1, 0}, {-1, 0}, {0 , 1}, {0, -1}};
int orangesRotting(vector<vector<int>>& grid) {
queue<pair<int, int>> q;
// 让坏橘子入队
for(int i = 0; i < grid.size(); ++i)
{
for(int j = 0; j < grid[0].size(); ++j)
{
if(grid[i][j] == 2)
{
q.push(make_pair(i, j));
}
}
}
int cnt = 0;
while(!q.empty())
{
size_t sz = q.size();
// 判断本次有无橘子腐烂
bool flag = false;
while(sz--)
{
auto curPos = q.front();
q.pop();
// 探查四个方向,判断新鲜橘子,将其腐烂并入队
for(int i = 0; i < 4; ++i)
{
int curx = curPos.first + nextMove[i][0];
int cury = curPos.second + nextMove[i][1];
// 判断是否越界
if(curx < 0 || curx >= grid.size() || cury < 0 || cury >= grid[0].size())
continue;
// 检测是否有新鲜橘子
if(grid[curx][cury] == 1)
{
// 本次有橘子腐烂
flag = true;
grid[curx][cury] = 2;
q.push(make_pair(curx, cury));
}
}
}
// 本次有橘子腐烂才能+时间
if(flag)
++cnt;
}
// 判断是否有新鲜橘子
for(int i = 0; i < grid.size(); ++i)
{
for(int j = 0; j < grid[0].size(); ++j)
{
if(grid[i][j] == 1)
{
return -1;
}
}
}
return cnt;
}
};
3. 单词接龙
原题链接:单词接龙
算法思想:
-
这道题要返回最小转化次数,可以使用DFS,但是由于堆栈开销,时间复杂度可能会比较大,这次我们使用BFS。
-
首先,将开始单词加入队列,遍历这个单词的每个字母,并分别对其进行变形,如果字典里存在变形后的单词,将其入队。
-
接着,按照队列的顺序将单词出队,遍历其每个字母,并分别对其进行变形,如果字典里存在变形后的单词,将其入队。
-
一轮变形结束后,变形次数+1.
-
重复2、3过程,直到本次遍历的单词和结束词相同,直接返回步数。
-
否则,队列为空结束,返回0。
-
代码实现:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_set<string> dict;// 存放wordList中的单词,方便查找
unordered_set<string> book;// 存放已经使用过的单词,方便查找
for(string& s : wordList)
dict.insert(s);
// 查找endWord是否在wordList中
if(!dict.count(endWord))
return 0;
queue<string> q; // 广度优先搜索队列
q.push(beginWord);
book.insert(beginWord);
int step = 1;
while(!q.empty())
{
int sz = q.size();
while(sz--)
{
string curStr = q.front();
q.pop();
if(curStr == endWord)
return step;
// 对每个字母进行变形比对
for(int i = 0; i < curStr.size(); ++i)
{
string tmp = curStr;
for(int j = 0; j < 26; ++j)
{
tmp[i] = 'a' + j;
// 如果wordList中有这个单词并且这个单词未使用过,入队
if(dict.count(tmp) && !book.count(tmp))
{
q.push(tmp);
book.insert(tmp);
}
}
}
}
step++;
}
return 0;
}
};
4. 最小基因变化
原题链接:最小基因变化
算法思想:
- 上一道题目的变式题,并且比上道题简单,交给大家完成。
代码实现:
class Solution {
public:
int minMutation(string start, string end, vector<string>& bank) {
unordered_set<string> dict;// 存放bank中的单词,方便查找
unordered_set<string> book;// 存放已经使用过的单词,方便查找
string change = "ACGT";
for(string& s : bank)
dict.insert(s);
// 查找end是否在bank中
if(!dict.count(end))
return -1;
queue<string> q; // 广度优先搜索队列
q.push(start);
book.insert(start);
int step = 0;
while(!q.empty())
{
int sz = q.size();
while(sz--)
{
string curStr = q.front();
q.pop();
if(curStr == end)
return step;
// 对每个字母进行变形比对
for(int i = 0; i < curStr.size(); ++i)
{
string tmp = curStr;
for(int j = 0; j < 4; ++j)
{
tmp[i] = change[j];
if(dict.count(tmp) && !book.count(tmp))
{
q.push(tmp);
book.insert(tmp);
}
}
}
}
step++;
}
return -1;
}
};
5. 打开转盘锁
原题链接:打开转盘锁
算法思想:
-
首先,将
0000加入队列,遍历这个字符串的每个字符,并分别对其每个数字进行向上和向下两种变形(eg. 向上:0->1,向下:1->0),如果密码不为deadends中的密码,将变形后的密码入队。 -
接着,按照队列的顺序将密码出队,遍历这个字符串的每个字符,并分别对其每个数字进行向上和向下两种变形(eg. 向上:0->1,向下:1->0),如果密码不为
deadends中的密码,将变形后的密码入队。 -
一轮变形结束后,变形次数+1.
-
重复2、3过程,直到本次遍历的密码和正确密码相同,直接返回变形次数。
-
否则,队列为空结束,返回-1。
代码实现:
class Solution {
public:
int openLock(vector<string>& deadends, string target) {
unordered_set<string> dead;// 存放deadends中的数据,方便查找
unordered_set<string> book;// 存放使用过的数据
for(string& s : deadends)
dead.insert(s);
// 判断0000是否在deadends中
if(dead.count("0000"))
return -1;
queue<string> q;
q.push("0000");
book.insert("0000");
int step = 0;
while(!q.empty())
{
int sz = q.size();
while(sz--)
{
string curStr = q.front();
q.pop();
if(curStr == target)
return step;
for(int i = 0; i < 4; ++i)
{
string tmp1 = curStr;
string tmp2 = curStr;
char ch1 = curStr[i]; // 向上滚动
char ch2 = curStr[i]; // 向下滚动
// 9再向上变形就是0
if(ch1 == '9')
ch1 = '0';
else
ch1 = ch1 + 1;
// 0再向下变形就是9
if(ch2 == '0')
ch2 = '9';
else
ch2 = ch2 - 1;
tmp1[i] = ch1;
tmp2[i] = ch2;
// 如果变形后的密码不等于dead数组中的密码且未使用过,直接入队
if(!dead.count(tmp1) && !book.count(tmp1))
{
q.push(tmp1);
book.insert(tmp1);
}
if(!dead.count(tmp2) && !book.count(tmp2))
{
q.push(tmp2);
book.insert(tmp2);
}
}
}
step++;
}
return -1;
}
};
后记
这些题是非常能体现出BFS思想的题目,虽然可能不是特别难,但都很经典,自己做一遍,总结思考一遍,基本就能记住这种思想。
BFS在图中也有很强的应用,许多算法也是基于BFS的思想得到的,未来白晨在讲图这个数据结构时会再次解释。
这是一个专门刷题的系列 ——【刷题日记】,白晨开这个系列的初衷是为了分享一些不同算法经典题型,以便于大家更好的学习编程。如果大家喜欢这个专栏的话——点击查看【刷题日记】所有文章。
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦!
如果这篇文章有帮到你,还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧!喜欢白晨【刷题日记】系列的话,不如关注白晨,以便看到最新更新哟!!!
我是不太能熬夜的白晨,我们下篇文章见。