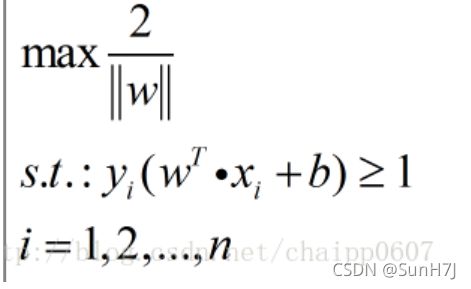机器学习之SVM公式推导及代码实现

SVM可分为以下三种情况：

①svm基本型：训练集在原始空间内就线性可分，找到最大间隔即可得到最优决策平面。

②软间隔支持向量机：训练集在原始空间内线性不可分，引入“soft margin软间隔”使其线性可分

③有核函数的svm：训练集在原始空间内线性不可分，将其映射到高维空间后（引入核函数）线性可分。

一、SVM基本型的推导

两个最重要的概念：

①支持向量support vector

离决策边界最近的样本称为支持向量support vector。

②间隔interval

两个异类（正类和反类）到决策边界的距离之和。

1.已知，样本空间中的超平面表达式是：

其中：表示超平面的方向，即：法向量；b表示其位置。

2.现样本空间中有两类样本，正类和反类。我们要找到一个最优决策边界（即一个超平面）将两类样本分开。

那怎么样的决策边界才是最优的呢？

那就是，当决策边界离两边最近的样本最远时。也就是，间隔最大时。

所以现在的目标，就是要找到：

有最大间隔的决策边界。

3.现在假设，

若样本满足：，就是正类，在决策边界左边，标签y=1；

若样本满足：，就是反类，在决策边界右边，标签y=-1。

 注：为什么这里取正负1？因为无论间隔距离是多少，都可以放缩为1.

4.容易计算出，和之间的距离。

由平行直线距离公式，|C1-C2|/√ (A²+B²)，可得：

     =        

即为决策边界的间隔。

5. 综上，可以得到SVM原型：

 s.t.为约束，即，两类样本必须分布在决策边界两边。

二、代码实现（待更新）

一、简单预热

1.导入相关模块

from sklearn.svm import SVC   

2.定义训练集

在此定义一个，有两个样本，每个样本有两个属性的样本集和一个对应的标签集。(注意python格式)

X = [[0, 0], [1, 1]]
Y = [0, 1]

由此可见，第一个样本【0,0】被分类为0，第二个样本【1,1】被分类为1

3.建立模型

建立核函数为‘linear’的支持向量机。     ？？待更新为什么是核函数为linear? 为什么模型要叫clf

clf = SVC(kernel='linear')

4.训练模型

用训练集训练模型，即：模型必须同时拟合样本集和标签集

clf = clf.fit(X, Y)

5.预测样本

用训练好了的模型clf，测试样本【2.， 2.】。   ？？为什么测试样本是这样的，为什么格式是【】】？？

clf.predict([[2., 2.]])

结果：
array([1])

可见，预测正确。 

二、案例应用（线性SVM）

1.导入相关模块

#导入数据处理模块
import numpy as np
import pandas as pd
#导入画图模块
import matplotlib.pyplot as plt
from scipy import stats
#默认使用seaborn进行图形展示
import seaborn as sns; sns.set()

2.读取数据

？？？什么意思

data=pd.read_csv('/data/shixunfiles/2d36301711d34324a3a0bc5865560cae_1577667399963.csv')
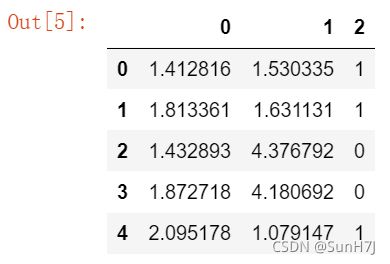
data.head()

输出：

可见，这是一个样本数为5，纬数为2，有标签的样本集。

3.提取特征值和标签值

4.数据展示

5.训练SVM

三、非线性SVM（引入核函数）

6.绘图

7.查看图像

8.获取支持向量