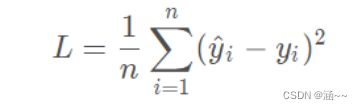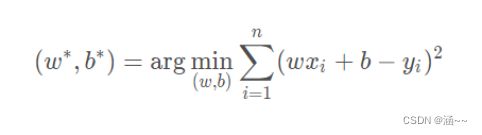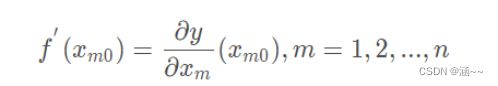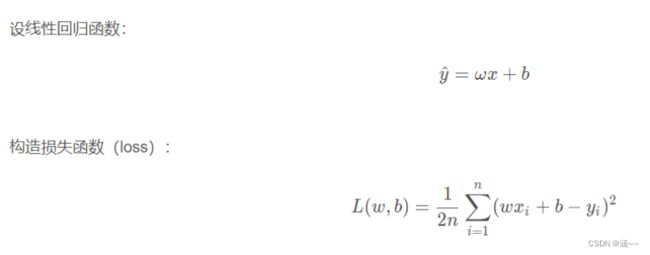一元线性回归
目录
一、线性回归概念
二、一元线性回归拟合
1、最小二乘法
1、基本思想
2、手工推导
3、代码实现
4、运行结果
2、梯度下降法
1、损失函数的构建
2、梯度下降三兄弟
3、梯度下降步骤
4、一元线性回归函数推导过程
三、实例
一、线性回归概念
线性回归,顾名思义,就是回归问题,既然是回归问题,那必然是监督学习,回归问题就是用于输入变量和输出变量之间的关系,特别当输入值发生变化时,输出值也会发生变化。回归模型正是表示从输入变量到输出变量之间映射的函数,回归问题的学习等价于函数拟合:选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
如果研究的线性函数只包含一个自变量和一个因变量,且二者的关系可以用一条直线刻画时,这种回归就是一元线性回归。如果涉及两个以上的自变量,且是线性关系,就称为多元线性回归。
二、一元线性回归拟合
拟合方法有最小二乘法和梯度下降法。
1、最小二乘法
1、基本思想
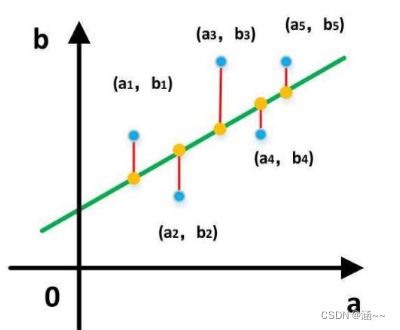
求出一些模型中未知参数使得样本点和拟合线的总误差最小最直观的感受如下图所示。
这个误差(距离)可以直接相减,但是直接相减会有正有负,相互抵消了,所以就用差的平方来表示。
2、手工推导
3、代码实现
import numpy as np
from matplotlib import pylab as pl
#Defining training data
x = np.array([1,3,2,1,3])
y = np.array([14,24,18,17,27])
# The regression equation takes the function
def fit(x,y):
if len(x) != len(y):
return
numerator = 0.0
denominator = 0.0
x_mean = np.mean(x)
y_mean = np.mean(y)
for i in range(len(x)):
numerator += (x[i]-x_mean)*(y[i]-y_mean)
denominator += np.square((x[i]-x_mean))
print('numerator:',numerator,'denominator:',denominator)
b0 = numerator/denominator
b1 = y_mean - b0*x_mean
return b0,b1
# Define prediction function
def predit(x,b0,b1):
return b0*x + b1
# Find the regression equation
b0,b1 = fit(x,y)
print('Line is:y = %2.0fx + %2.0f'%(b0,b1))
# prediction
x_test = np.array([0.5,1.5,2.5,3,4])
y_test = np.zeros((1,len(x_test)))
for i in range(len(x_test)):
y_test[0][i] = predit(x_test[i],b0,b1)
# Drawing figure
xx = np.linspace(0, 5)
yy = b0*xx + b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
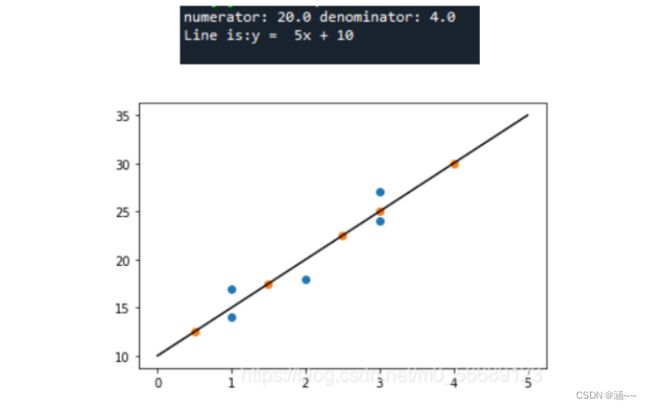
pl.show()4、运行结果
2、梯度下降法
1、损失函数的构建
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好, 通常模型的性能越好。不同的模型用的损失函数一般也不一样。在应用中,通常通过最小化损失函数求解和评估模型。
针对任何模型求解问题,最后都可以得到一组预测值,对比已有的真实值,数据行数为n,可以知道:
即预测值与真实值之间的平均距离,统计称为均方误差。把之前的函数带入损失函数,并且将需要求解的w,b看作自变量,可得:
核心表达式为:
2、梯度下降三兄弟
2.1 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法每次都使用训练集中的所有样本更新参数。它得到的是一 个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果m很 大,那么迭代速度就会变得很慢。 优点:可以得出全局最优解。 缺点:样本数据集大时,训练速度慢
2.2 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法每次更新都从样本随机选择1组数据,因此随机梯度下降比 批量梯度下降在计算量上会大大减少。SGD有一个缺点是,其噪音较BGD 要多,使得SGD并不是每次迭代都向着整体最优化方向。而且SGD因为每 次都是使用一个样本进行迭代,因此最终求得的最优解往往不是全局最优 解,而只是局部最优解。但是大的整体的方向是向全局最优解的,最终的 结果往往是在全局最优解附近。 优点:训练速度较快。 缺点:过程杂乱,准确度下降。
2.3小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法对包含n个样本的数据集进行计算。综合了上述两种方 法,既保证了训练速度快,又保证了准确度。
3、梯度下降步骤
假设函数:y = f ( x 1 , x 2 , x 3 . . . . x n ) 只有一个极小点。
初始给定参数为X 0 = ( x 1 0 , x 2 0 , x 3 0.... x n 0 ) 。
从这个点如何搜索才能找到 原函数的极小值点?
方法:
①首先设定一个较小的正数 α , ε;
②求当前位置出处的各个偏导数:
③修改当前函数的参数值,公式如下:
④如果参数变化量小于 ,退出;否则返回第2步。
4、一元线性回归函数推导过程
思路:通过梯度下降法不断更新 和 ,当损失函数的值特别小时,就得到
了我们最终的函数模型。
过程:
三、实例
波士顿房价问题
使用梯度下降求解线性回归
代码实现:
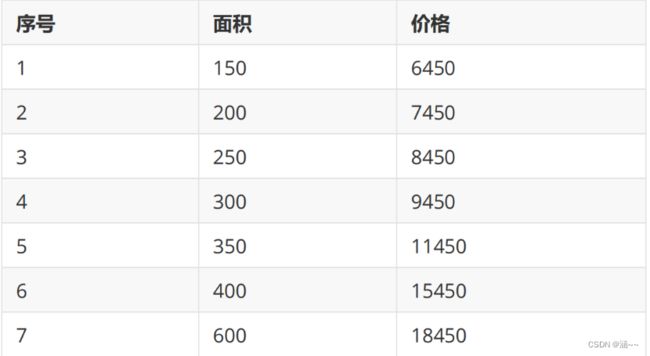
1.#房屋价格与面积
2.#序号:1 2 3 4 5 6 7
3.#面积:150 200 250 300 350 400 600
4.#价格:6450 7450 8450 9450 11450 15450 18450
5.import matplotlib.pyplot as plt
6.import matplotlib
7.from math import pow
8.import random
9.x0 = [150,200,250,300,350,400,600]
10.y0 = [6450,7450,8450,9450,11450,15450,18450]
11.#为了方便计算,将所有数据缩小 100 倍
12.x = [1.50,2.00,2.50,3.00,3.50,4.00,6.00]
13.y = [64.50,74.50,84.50,94.50,114.50,154.50,184.50]
14.#线性回归函数为 y=theta0+theta1*x
15.#损失函数 J (θ)=(1/(2*m))*pow((theta0+theta1*x[i]-y[i]),2)
16.#参数定义
17.theta0 = 0.1#对 theata0 赋值
18.theta1 = 0.1#对 theata1 赋值
19.alpha = 0.1#学习率
20.m = len(x)
21.count0 = 0
22.theta0_list = []
23.theta1_list = []
24.#1.使用批量梯度下降法
25.for num in range(10000):
26. count0 += 1
27. diss = 0 #误差
28. deriv0 = 0 #对 theata0 导数
29. deriv1 = 0 #对 theata1 导数
30. #求导
31. for i in range(m):
32. deriv0 += (theta0+theta1*x[i]-y[i])/m#对每一项测试数据求导再求和取平均值
33. deriv1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]
34. #更新 theta0 和 theta1
35. theta0 = theta0 - alpha*deriv0
36. theta1 = theta1 - alpha*deriv1
37. #求损失函数 J (θ)
38. for i in range(m):
39. diss = diss + (1/(2*m))*pow((theta0+theta1*x[i]-y[i]),2)
40.
41. theta0_list.append(theta0*100)
42. theta1_list.append(theta1)
43. #如果误差已经很小,则退出循环
44. if diss <= 0.001:
45. break
46.theta0 = theta0*100#前面所有数据缩小了 100 倍,所以求出的 theta0 需要放大 100 倍,theta1 不用变
47.#2.使用随机梯度下降法
48.theta2 = 0.1#对 theata2 赋值
49.theta3 = 0.1#对 theata3 赋值
50.count1 = 0
51.theta2_list = []
52.theta3_list = []
53.for num in range(10000):
54. count1 += 1
55. diss = 0 #误差
56. deriv2 = 0 #对 theata2 导数
57. deriv3 = 0 #对 theata3 导数
58. #求导
59. for i in range(m):
60. deriv2 += (theta2+theta3*x[i]-y[i])/m
61. deriv3 += ((theta2+theta3*x[i]-y[i])/m)*x[i]
62. #更新 theta0 和 theta1
63. for i in range(m):
64. theta2 = theta2 - alpha*((theta2+theta3*x[i]-y[i])/m)
65. theta3 = theta3 - alpha*((theta2+theta3*x[i]-y[i])/m)*x[i]
66. #求损失函数 J (θ)
67. rand_i = random.randrange(0,m)
68. diss = diss + (1/(2*m))*pow((theta2+theta3*x[rand_i]-y[rand_i]),2)
69.
70. theta2_list.append(theta2*100)
71. theta3_list.append(theta3)
72. #如果误差已经很小,则退出循环
73. if diss <= 0.001:
74. break
75.theta2 = theta2*100
76.print("批量梯度下降最终得到theta0={},theta1={}".format(theta0,theta1))
77.print(" 得到的回归函数是:y={}+{}*x".format(theta0,theta1))
78.print("随机梯度下降最终得到theta0={},theta1={}".format(theta2,theta3))
79.print(" 得到的回归函数是:y={}+{}*x".format(theta2,theta3))
80.#画原始数据图和函数图
81.matplotlib.rcParams['font.sans-serif'] = ['SimHei']
82.plt.plot(x0,y0,'bo',label='数据',color='black')
83.plt.plot(x0,[theta0+theta1*x for x in x0],label='批量梯度下降',color='red')
84.plt.plot(x0,[theta2+theta3*x for x in x0],label='随机梯度下降',color='blue')
85.plt.xlabel('x(面积)')
86.plt.ylabel('y(价格)')
87.plt.legend()
88.plt.show()
89.plt.scatter(range(count0),theta0_list,s=1)
90.plt.scatter(range(count0),theta1_list,s=1)
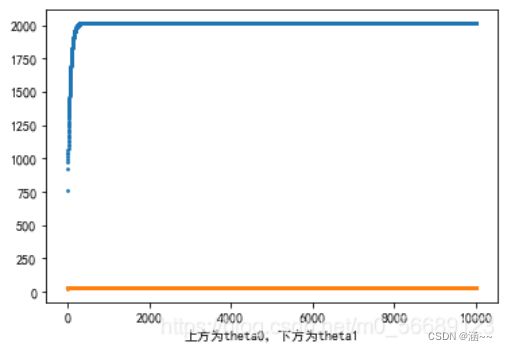
91.plt.xlabel('上方为theta0,下方为theta1')
92.plt.show()
93.plt.scatter(range(count1),theta2_list,s=3)
94.plt.scatter(range(count1),theta3_list,s=3)
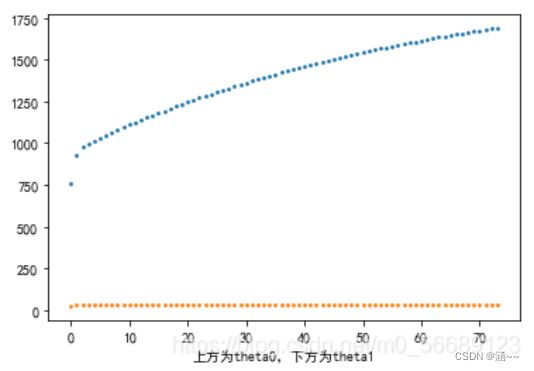
95.plt.xlabel('上方为theta0,下方为theta1')
96.plt.show()输出结果:
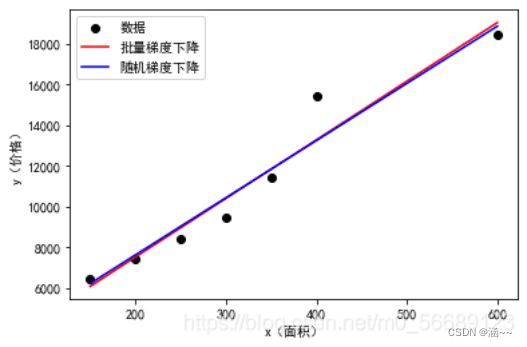
线性回归函数图像:
梯度下降时theta0和theta1的变化:
随机梯度下降时的theta0和theta1的变化: