【机器学习】第一章 - 机器学习概论 - 周志华机器学习笔记
【机器学习】第一章 - 机器学习概论 - 周志华机器学习笔记
- 基本术语
-
- 假设空间 & 版本空间
- 归纳偏好
-
- 为什么需要归纳偏好?- 从版本空间中找出最准确的假设
- 如何引导算法确立“正确的”偏好?- 奥卡姆剃刀
- 没有免费的午餐 - 所有算法的期望性能相同
- 为什么还要学习算法(既然没有免费午餐)?- NFL考虑所有问题,但更应该具体问题讨论具体算法
基本术语
数据集(data set):样本集合。
示例(instance):样本(sample),数据集中的每条记录。关于一个事件或对象(这里是一个西瓜)的描述。
特征(feature):又称 属性(attribute),反映事件或对象在某方面的表现或性质的事项。
属性值(attribute value):属性的值。
属性空间(attribute space):属性张成的空间。
样本空间(sample space):输入空间。
特征向量(feature vector):由于空间中的每个点对应一个坐标向量,因此把一个示例称为一个特征向量。
标记(label):
样例(example):
标记空间(label space):
分类(classification):
回归(regression):
二分类(binary classification):
正类(positive class):二分类问题中一个类。
反类(negative class):二分类问题中另一个类。
多分类(multi-class classification):涉及多个类别的分类。
训练(training):从数据中学得模型的过程。
训练数据(training data):训练过程中使用的数据。
训练样本(training sample):训练数据中的一个样本。
训练集(training set):训练样本组成的集合。
测试(testing):
测试样本(testing sample):
聚类(clustering):
簇(cluster):
泛化(generalization): 有训练集学习得到的模型适用于新样本的能力
【待补充】
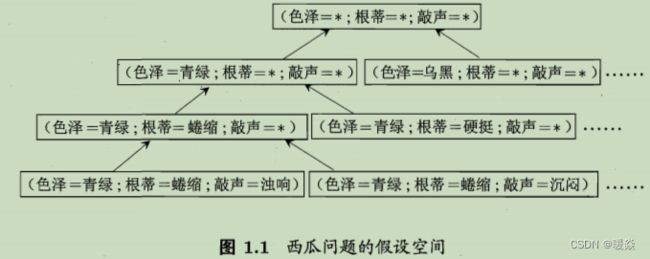
假设空间 & 版本空间
假设空间:一个由所有假设(hypothesis)组成的空间。
学习过程,可看做在假设空间中进行搜索的过程,搜索目标是找到与训练集“匹配”(fit)的假设。
假设的表示一旦确定,假设空间及其规模大小就确定了。
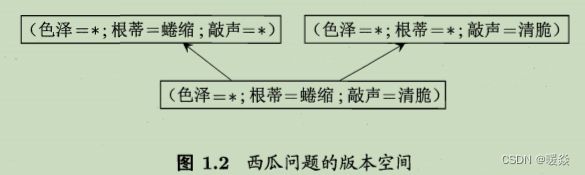
版本空间:现实问题中常面临很大的假设空间,但学习过程是基于有限样本训练集进行的,因此,可能有多个假设与训练集一致,即存在着一个与训练集一致的“假设集合”,称之为“版本空间”(version space)。
归纳偏好
机器学习算法在学习过程中对某种类型假设的偏好,称为 “归纳偏好”(inductive bias), 或简称为“偏好”。
为什么需要归纳偏好?- 从版本空间中找出最准确的假设
因为是使用同一训练样本集进行学习,所以无法判断版本空间中的多个假设的好坏,对于一个具体的学习算法而言,它必须要产生一个模型。这时,学习算法本身的“偏好”就会起到关键的作用。
任何一个有效的机器学习算法必有其归纳偏好,否则它将被假设空间中在同一训练集上“等效”的假设所迷惑,而无法产生确定的学习结果。如果没有偏好,西瓜学习算法产生的模型每次在进行预测时随机抽选训练集上的等效假设,那么将新样本输入模型,时而告诉我们它是好的、时而告诉我们它是不好的,这样的学习结果显然没有意义。
图1.3回归学习图示中,每个训练样本是图中的一个点(x,y),要学得一个与训练集一致的模型,相当于找到一条穿过所有训练样本点的曲线。显然,对有限个样本点组成的训练集,存在着很多条曲线与其一致。我们的学习算法必须有某种偏好,才能产出它认为“正确”的模型。
例如,若认为相似的样本应有相似的输出(例如,在各种属性上都很相像的西瓜,成熟程度应该比较接近),则对应的学习算法可能偏好图 1.3 中比较 “平滑”的曲线A 而不是比较“崎岖”的曲线B)。
如何引导算法确立“正确的”偏好?- 奥卡姆剃刀
“奥卡姆剃刀" (Occam’s razor)是一种常用的、 自然科学 研究中最基本的原则,即 “若有多个假设与观察一致,则选最简单的那个”。奥卡姆剃刀并非唯一可行的原则,奥卡姆剃刀本身存在不同的诠释,使用奥卡姆剃刀原则并不平凡,需借助其他机制才能解决。
没有免费的午餐 - 所有算法的期望性能相同
根据奥卡姆剃刀原则,在上图A和B两个假设中,A更简单,所以A优于B,但是,会不会出现现图1.4(b)的 情况:与 A 相比,B 与训练集外的样本更一致?
与 A 相比,B 与训练集外的样本更一致,这种情况完全可能出现。换句话说,对于一个学习算法 a ,若它在某些问题上比学习算法 b 好,则必然存在另一些问题中 b 算法比 a 算法好。
没有免费的午餐定理理 (No Free Lunch Theorem,简称NFL定理)对任何算法均成立,哪怕是把本书后面将要介绍的一些聪明算法作为 a 而将 “随机胡猜”这样的笨拙算法作为 b,没有免费的午餐定理仍然成立。
训练集外所有样本上的总误差与学习算法无关,对于任意两个学习算法 a, b,无论算法 a 多聪明,无论算法 b 多笨拙,两种算法的期望性能相同。
为什么还要学习算法(既然没有免费午餐)?- NFL考虑所有问题,但更应该具体问题讨论具体算法
N FL定理有一个重要前提:所有 “问题” 出现的机会相同、或所有问题同等重要。但实际情形并不是这样。很多时候,我们只关注自己正在试图解决的问题(例如某个具体应用任务),希望为它找到一个解决方案, 至于这个解决方案在别的问题、甚至在相似的问题上是否为好方案,我们并不关心。
例如,为了快速从A 地到达 B 地,如果我们正在考虑的 A 地是南京鼓 楼、B 地是南京新街口,那 么 “骑自行车”是很好的解决方案;这个方案对A 地是南京鼓楼、B 地是北京新街口的情形显然很糟糕,但我们对此并不关心。
NFL定理的简短论述过程中假设了 f 的均匀分布,而实际情形并非如此。
例如:在西瓜例子中,对于品种1好瓜 假设1 更好,对于品种2好瓜 假设2 更好,但 品种1 的好瓜很常见,品种2 的好瓜却很罕见甚至不存在。
NFL定理最重要的寓意,是让学习者清楚地认识到,脱离具体问题,空泛地谈论“什么学习算法更好”毫无意义,因为若考虑所有潜在的问题,则所有学习算法都一样好。要谈论算法的相对优劣,必须要针对具体的学习问题;在某些问题上表现好的学习算法,在另一些问题上却可能不尽如人意,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性的作用。