改进粒子速度和位置更新公式的粒子群优化算法

改进粒子速度和位置更新公式的粒子群优化算法

摘要：针对粒子群优化算法求解精度低、局部搜索能力差、进化后期收敛速度慢等问题，本文提出一种改进粒子速度和位置更新公式的粒子群优化算法（particle swarm optimization algorithm with improved particle velocity and position update formula, IPSO-VP）. IPSO-VP算法提出一种自适应粒子速度和位置更新策略，采用基于Logistic混沌呈非线性变化的惯性权重，以此来加快算法的收敛速度、平衡算法的全局和局部搜索能力、提高收敛精度.

1.粒子群优化算法

基础粒子群算法的具体原理参考网络资料

2. 改进粒子群算法

2.1 粒子速度和位置自适应更新策略

本文结合以上分析提出一种新的自适应粒子速度和位置更新策略,如式 (10)、(11)所示.
$$\begin{array}{r}\{\begin{array}{rl}{v}_{id}(t+1)& =w{v}_{id}(t)+c_1{r}_1\left(\frac{{\text{ pbest }}_{id}+{\text{ ghest }}_d}{2}-x_{id}(t)\right)+c_2{r}_2\left(\frac{{\text{ pbest }}_{id}-{\text{ gbest }}_d}{2}-x_{id}(t)\right),\\ x_{id}(t+1)& =w{x}_{id}(t)+(1-w)v_{id}(t+1)\end{array}\end{array}\text{\hspace{1em}(10)}$$

$$\begin{array}{r}\{\begin{array}{l}{v}_{id}(t+1)=w{v}_{id}(t)+c_1{r}_1\left(p_{ad}-x_{id}(t)\right)+c_2{r}_2\left({\text{ gbest }}_d-x_{id}(t)\right),\\ x_{id}(t+1)=x_{id}(t)+v_{id}(t+1)\end{array}\end{array}\text{\hspace{1em}(11)}$$
上述自适应策略借鉴文献 $[8]$ 中 $p_i$ 作为自适应判定条件. 当 $p_i>\delta$ 时,当前粒子的适应度值远大于种群中 所有粒子平均适应度值, 表明算法处于搜索初期或者当前粒子分布较为分散,此时应采用式 (10)更新粒 子速度和位置. 式 $(10)$ 在速度更新项中引人个体最优和群体最优的线性组合, 能够使粒子的搜索空间更 广, 从而提高算法搜索到全局最优解的可能性,而位置更新则采用 “ $X=wX+(1-w)V$ ” 来提高算法的全局搜 索能力; 当 $p_i<\delta$ 时, 当前粒子的适应度值与种群中所有粒子平均适应度值相差不大, 表明算法处于搜索中 后期或者当前粒子分布较为集中, 此时应采用式 (11) 更新粒子速度和位置. 在式 (11) 中, 位置更新采用 “ $X=X+V$ ” 来保证算法局部勘探能力, 防止算法在求解复杂多峰函数时陷人局部最优, 而将粒子平均维度 信息 $p_{ad}$ 引人到粒子速度更新公式中, 提高算法的收敛速度 .

2.2 惯性权重的选取

惯性权重 $w$ 是 PSO 算法的重要参数之一, 它可以平衡算法全局开发能力和局部勘探能力, 标准 PSO 算法采用线性递减 $w$, 这种线性调整的方式可以在一定程度上平衡算法开发能力与勘探能力, 而在面对复 杂非线性多维函数优化问题时, 算法容易陷人局部最优解. 因此, 为更好改善算法性能, 一些学者提出惯 性权重非线性调整策略. 本文采用文献 $[8]$ 提出的基于 Logistic 混沌映射非线性变化惯性权重 $w$.

混沌映射作为一种非线性映射, 因其所产生的混沌序 列具有良好随机性和空间遍历性,在进化计算中得到广泛 应用,其中 Logistic 映射应用较为广泛, 它可以产生 $[0,1]$ 之 间的随机数. 式 (12) 给出了 Logistic 映射的定义, $w$ 的定义 如式 (13).
$$\begin{array}{c}r(t+1)=4r(t)(1-r(t)),r(0)=\text{ rand }\\ \text{ 其中 },r_0\ne \{0,0.25,0.75,1\},\\ w(t)=r(t)w_{\text{min }}+\frac{\left(w_{\max }-w_{\min }\right)t}{T_{\max }},\end{array}$$
式中, $w_{\text{max }}=0.9,w_{\text{min }}=0.4;r(t)$ 是由式 (12) 迭代产生的随机 数.

算法实现步骤如下:
步骤 1 参数初始化, 包括种群规模 $N$, 最大迭代次数 $T_{\max }=1000$, 学习因子 $c_1$ 和 $c_2$, 惯性权重 $w$; 并在 搜索空间内随机初始化粒子位置、速度;
步骤 2 根据给定目标函数计算所有粒子适应度值;
步骤 3 比较种群中所有粒子的适应度值与其经历过的最优位置适应度值的优劣, 若前者更优, 则用 粒子的当前位置替代粒子的个体历史最优位置;
步骤 4 比较种群中所有个体最优位置的适应度值与整个群体经历过的最优位置的适应度值的优 劣, 若前者更优,则更新全局最优位置;
步骤 5 根据式 (8) 计算 $p_i$, 若 $p_i>\delta$, 则利用式 (10) 更新粒子的速度和位置; 否则, 利用式 (11) 更新粒 子的速度和位置;
步骤 6 判断是否满足终止条件, 若满足, 则算法终止并输出最优值; 否则, 转至步骤 2 .

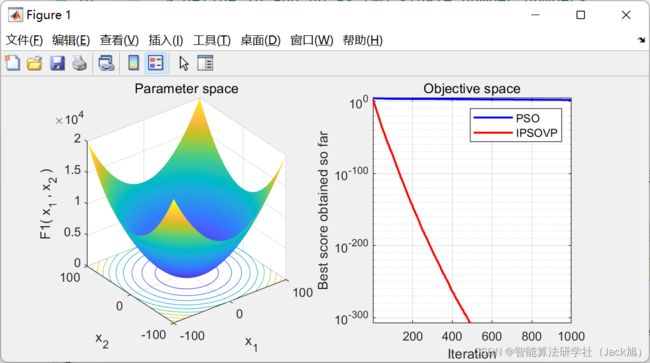
3.实验结果

4.参考文献

[1]李二超,高振磊.改进粒子速度和位置更新公式的粒子群优化算法[J].南京师大学报(自然科学版),2022,45(01):118-126.

5.Matlab代码

6.Python代码