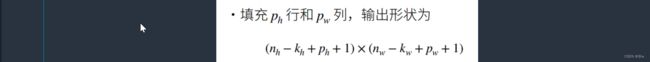【动手学深度学习PyTorch版】13 卷积层的填充和步幅

上一篇移步【动手学深度学习PyTorch版】12 卷积层_水w的博客-CSDN博客

目录

一、卷积层的填充和步幅

1.1 填充

1.2 步幅

1.3 总结

二、代码实现填充和步幅（使用框架）

---

一、卷积层的填充和步幅

1.1 填充

假设我们给出一个输入图像的大小为（32x32），图片比较小的时候，那么如果应用一个大小为5x5的卷积核，输出就会减少4x4，也就是说（32x32）变成了[（32-5+1）x（32-5+1）]=（28x28）。

如果用7层，那么我们得到的输出就是（4x4），而且我们用更大的卷积核的话，可以更快的减少输出的大小，

所以卷积层的输出形状由输入形状和卷积核窗口形状决定。填充和步幅。它们可以对给定形状的输入和卷积核改变输出形状。

那么就会有个问题：假设我不想要我的输出变得这么小，应该怎么办？如果我想要做更深的卷积层怎么办？

解决这个问题的第一个办法：填充，

可以在输入的周围添加额外的行或者列，让我们的输出变得比以前更加大。

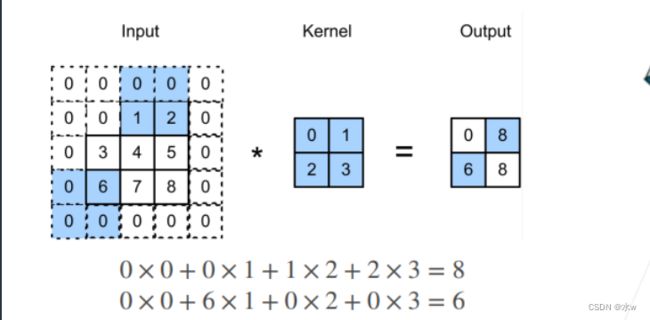
比如，下图中，我们在输入的周围添加额外的行0或者列0，然后滑动窗口，得到输出。

填充之后，我们就相当于多了参数Ph和Pw，

原输入数组形状是Nh×Nw，卷积核形状是Kh×Kw，那么原输出数组形状就是

(Nh-Kh+1)×(Nw-Kw+1)。如果我们对输入数组进行填充高加Ph，宽加Pw，那么新的输出数组形状就是(Nh-Kh+Ph+1)×(Nw-Kw+Pw+1)。

通常我们为了方便在构造网络时推测每个层的输出形状，会设置Ph=Kh-1，Pw=Kw-1。这样输入输出形状就是一致的，是为了将Ph和Pw的值代入进去式子的时候，就可以消去。

也就是说，我的输出和输入的大小不会发生变化，都是Nh和Nw。这是一个挺好的东西， 不管我们选取的核的大小，都不会改变输出和输入的大小。

具体说填充，我们可以在上或者下填充，

① 奇数卷积核更容易做padding。我们假设卷积核大小为k * k，为了让卷积后的图像大小与原图一样大，根据公式可得到padding=（k-1）/2，这里的k只有在取奇数的时候，padding才能是整数，否则padding不好进行图片填充。

② k为偶数时，p为浮点数，所做的操作为一个为向上取整，填充，一个为向下取整，填充。

1.2 步幅

假设我们的输入变成了（254x254），假设我想要输出的大小为4x4，那么在使用5x5卷积核的情况下，需要55层才能将输出降低到4x4，这就比较痛苦了。

因为层数越多计算就越复杂，需要大量的计算才能得到较小的输出。

可以使用步幅：行/列的滑动步长来解决这个问题。

因为之前输出的大小是跟层数呈现线性相关的，那使用步幅可以让输出的大小跟层数变成指数相关。

假设我们的核还是2x2，使用步幅的高度为3，宽度为2，

输出Y的第一个元素还是0，但是到输出Y的第2个元素“8”时，下一个不再是之前我们考虑的绿框了（默认步幅为1），而是往右移两点，直接变成了红框，

再往右跳2的话，由于没有足够的值了，所以输出的宽度就为2。

同理，在高度上，类似。

当我们不做步幅的调整，即默认步幅为1，那么输出的大小为4x4。

现在使用了步幅之后，我们就直接把我们的5x5大矩阵变成了一个2x2的小矩阵了。

这就是步幅的概念，在每次滑动窗口的时候，控制滑动的行数或者列数，成倍的减少输出的形状。

1.3 总结

参数：

in_channels：输入的通道数目
out_channels： 输出的通道数目
kernel_size：卷积核的大小，类型为int 或者元组，当卷积是方形的时候，只需要一个整数边长即可，卷积不是方形，要输入一个元组表示 高和宽。
stride： 卷积每次滑动的步长为多少，默认是 1
padding： 设置在所有边界增加 值为 0 的边距的大小（也就是在feature map 外围增加几圈 0 ），例如当 padding =1 的时候，如果原来大小为 3 × 3 ，那么之后的大小为 5 × 5 。即在外围加了一圈 0 。
dilation：控制卷积核之间的间距
groups：控制输入和输出之间的连接
bias： 是否将一个 学习到的 bias 增加输出中，默认是 True 。
padding_mode ： 字符串类型，接收的字符串只有 “zeros” 和 “circular”。

二、代码实现填充和步幅（使用框架）

（1）输入和输出通道为1，核大小为3x3，填充padding=1 为上下左右都填充一行。

随机生成8x8的矩阵，输入通道为1，输出通道为1，卷积核大小为1x2的，没有设置步长与边界，步长默认为1。

放入函数comp_conv2d(conv2d,X)，此时的Ph为2，Pw为2，可以看到我们的输出也是8x8。

# 在所有侧边填充1个像素
import torch
from torch import nn

def comp_conv2d(conv2d, X): # conv2d 作为传参传进去，在内部使用
    X = X.reshape((1,1)+X.shape) # 输入通道为1，输出通道为1，在维度前面加入一个通道数和批量大小数
    Y = conv2d(X)  # 卷积处理是一个四维的矩阵
    return Y.reshape(Y.shape[2:]) # 将前面两个维度拿掉，得到一个矩阵输出

conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1)  # 输入和输出通道为1，核大小为3x3，填充padding=1 为上下左右都填充一行
X = torch.rand(size=(8,8))
print(comp_conv2d(conv2d,X).shape)

是因为上下左右各填充一行，核大小为3x3的话，（8x8）---->（8-3+Ph+1）x（8-3+Pw+1）---->（8-3+2+1）x（8-3+2+1）---->（8）x（8），就不会对输入的大小做什么变化。

（2）当然，我们也可以不那么对称，可以填充不同的高度和宽度。

此时，卷积核的大小为5x3，还是想让输入和输出的大小是一样的话，那么（8x8）---->（8-3+Ph+1）x（8-5+Pw+1），可以计算得到Ph为2，Pw为4，那么上下填充padding应该是2，左右填充padding的列数应该是1，

conv2d = nn.Conv2d(1,1,kernel_size=(5,3),padding=(2,1))
print(comp_conv2d(conv2d,X).shape)

 如果这样设置的话，那么输入和输出还是一样的大小。

（4） 填充padding=2 为上下左右都填充2行，

随机生成8x8的矩阵，输入通道为1，输出通道为1，卷积核大小为3x3的，边界左右扩展1，上下扩展1，步长为2。

那么如果没有“stride=2”的话我们的输出还是8x8，有“stride=2”之后，因为输入的高宽可以被整除，那么输出是从8x8变成了4x4。

# 将高度和宽度的步幅设置为2
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2)
print(comp_conv2d(conv2d,X).shape)

（5）看一个稍微复杂，做一个完全不对称的情况，可以控制在行和列上每一次的卷积的大小。

输入X为8×8，输入通道为1，输出通道为1，卷积核为3×5，边界扩展1，左步长为3，右步长为4。 

# 一个稍微复杂的例子
conv2d = nn.Conv2d(1,1,kernel_size=(3,5),padding=(0,1),stride=(3,4))
print(comp_conv2d(conv2d,X).shape)

那么得到是数组形状是⌊(8-3+0+3)/3⌋=2， (8-5+1+4)/ 4 = 2。