2017-Attention Is All You Need
文章目录
- 1. Title
- 2. Summary
- 3. Problem Statement
- 4. Method(s)
-
- 4.1 Encoder and Decoder Stacks
-
- 4.1.1 Encoder
- 4.1.2 Decoder
- 4.2 Attention
-
- 4.2.1 Scaled Dot-Product Attention
- 4.2.2 Multi-Head Attention
- 4.2.3 Applications of Attention in Transformer
- 4.3 Position-wise Feed-Forward Networks
- 4.4 Positional Encoding
- 5. Evaluation
- 6. Conclusion
1. Title
文章链接:Attention Is All You Need
代码链接:https://github.com/jadore801120/attention-is-all-you-need-pytorch
2. Summary
在经典的序列翻译模型中,大都是基于RNN和CNN来完成。RNN并行化能力差,CNN捕获远距离依赖的代价较高。基于以上考虑,本文提出了一个仅仅基于Attention机制的Transformer结构,其并行化能力高,同时可以很高效地捕获远距离依赖,克服了RNN和CNN的缺点,成为了NLP领域的标准模型。
3. Problem Statement
目前领先的序列翻译模型大都基于复杂的循环神经网络或是包含解码器和编码器的卷积神经网络。
- RNN会根据前一个隐状态 h t − 1 h_{t-1} ht−1以及当前位置 t t t去产生一个新的隐状态 h t h_t ht,也就是说当前的输出依赖于之前的输出,网络无法并行化地去处理不同的位置,这会导致网络并行化能力较差,当序列较长时,由于内存限制,将会限制batchsize的大小,不利于加速网络的训练。
- CNN并行化能力较强,但本身仅具有局部感受野,只有通过堆叠多个卷积或是使用空洞卷积,才能逐步扩大感受野,从而捕获远程依赖,但所需要的资源也会较多,网络也较难训练。
4. Method(s)
为了消除循环和卷积网络,本文则是提出了一种简单的神经网络架构——Transformer,一个仅由Attention机制组成的网络,从而可以更高效地去捕获远程依赖。这种结构具有良好的并行化能力,并且训练时间也更短。
Transformer仍然采取了大部分序列翻译网络的Encoder-Decoder结构:
- Encoder:将输入的符号表示序列 x = ( x 1 , . . . , x n ) x=(x_1,...,x_n) x=(x1,...,xn)转化为一个连续的表示序列 z = ( z 1 , . . . , z n ) z=(z_1,...,z_n) z=(z1,...,zn)。
- Decoder:根据 z z z生成一个符号表示序列 y = ( y 1 , . . . , y m ) y=(y_1,...,y_m) y=(y1,...,ym),每次前传过程中,仅会生成一个 y i y_i yi。
模型以一种Auto-Regressive的方式运行,在生成下一个符号 y i y_i yi时,会将之前生成的符号序列 ( y 1 , y 2 , . . . , y i − 1 ) (y_1,y_2,...,y_{i-1}) (y1,y2,...,yi−1)作为附加输入。
Transformer的Encoder以及Decoder均由堆叠而成的自注意力模块以及全连接神经网络构成,其整体结构如下图所示:

4.1 Encoder and Decoder Stacks
4.1.1 Encoder
Encoder的Inputs是待翻译的序列。
Encoder由 N = 6 N=6 N=6个相同的layer组成,每个layer包含两个sub-layers:
- Multi-Head Self-Attention Network
- Position-wise Fully Forward Network
每个sub-layer都带有一个残差连接,并在最后接一个Layer Normalization,也就是说每个sub-layer的输出为LayerNorm(x+Sublayer(x))。
所有的sub-layer以及embedding layer输出的维度为 d m o d e l = 512 d_{model}=512 dmodel=512。
4.1.2 Decoder
Transformer结构图中Decoder的Outputs(实际上是Decoder的一个Input)是待翻译序列的真值结果,仅在训练时提供。
Decoder也由 N = 6 N=6 N=6个相同的layer组成,除了和Encoder中相同的两个sub-layers以外,Decoder还有第三个sub-layer,用于对来自Encoder的堆叠的输出进行multi-head Attention。
同时考虑到当前时刻t的Attention不应该来自于未来,而Decoder的Outputs是一个完整的序列,因此,需要对当前时刻t之后的序列信息进行屏蔽,也就是用mask进行”遮蔽“,得到图中的Masked Multi-Head Attention。
这里简单解释一下Mask的作用。
首先需要明确一下Transformer的训练过程,特别是Decoder的解码过程。
Encoder的编码过程可以用矩阵运算并行计算,但是Decoder的解码过程却不能一次性把所有序列解码出来,而是采用一种Auto-Regressive的方式,一次只能解码出一个词,直到遇到一个特殊的终止符号才停止解码。
训练过程中,Decoder的Outputs是真值序列,是一个完整的真值序列,由于Self-Attention的全局感受野的缘故,解码过程中,每个query都会“看到”所有的key,并产生相应的权重,而这显然是不合理的,当前的query应该仅能“看到”当前query之前的所有key才行。而Mask正是起到这样的作用。
在实际实现过程中,每个query会计算与所有key的权重,但是会通过相应的mask将当前query之后的权重全部设置为一个特别小的值,后续经过Softmax之后,这些特别小的权重变不会对最终的输出产生明显的影响,即可实现当前的query仅能“看到”当前query之前的所有key的作用。
4.2 Attention
Attention机制可以描述为:将一个query和一个key-value对映射为一个output,其中query、key、value以及output均为向量。
output是value的一个weighted-sum,而其weight则是来自query以及key之间的一种相似度。
4.2.1 Scaled Dot-Product Attention

Transformer采用的是一种Scaled Dot-Product Attention。输入queries以及keys的维度为 d k d_k dk,values的维度为 d v d_v dv,具体计算时,这些向量会被拼接为矩阵进行运算,从而实现极高的并行化,计算公式为: A t t e n i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attenion(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attenion(Q,K,V)=softmax(dkQKT)V目前有两种较为常见的attention计算方式:
-
Additive attention:
加性注意力机制计算注意力得分的公式为 s ( p i , q ) = V T t a n h ( W p i + U q ) s(p_i,q)=V^Ttanh(Wp_i+U_q) s(pi,q)=VTtanh(Wpi+Uq)
计算注意力分布的公式为 α i = s o f t m a x ( s ( p i , q ) ) = e x p ( s ( p i , q ) ) ∑ j e x p ( s ( p j , q ) ) \alpha_i=softmax(s(p_i,q))=\frac{exp(s(p_i,q))}{\sum_j{exp(s(p_j,q))}} αi=softmax(s(pi,q))=∑jexp(s(pj,q))exp(s(pi,q))
加性注意力公式为: s ( p i , q ) = V T t a n h ( W p p i + w q q + b ) s(p_i,q)=V^Ttanh(W_pp_i+w_qq+b) s(pi,q)=VTtanh(Wppi+wqq+b)。 -
Dot-product attention:点积注意力机制与本文使用的attention机制相同,仅仅是少了一个scaling factor 1 d k \frac{1}{\sqrt{d_k}} dk1
尽管理论上,加性和乘性注意力两者在计算复杂度是相似的,但是在实际使用过程中,由于可以使用高度优化的矩阵计算,点乘注意力更快也更为节省空间。
在Transformer中,当 d k d_k dk较小时,两种注意力的性能较为类似,当 d k d_k dk较大时,加性注意力机制会略微优于不带放缩因子的点乘注意力,可能原因在于当 d k d_k dk较大时,点积可能会很大,落入到了Softmax的小梯度区,因此,Transformer使用了一个放缩因子去消除这个问题。
4.2.2 Multi-Head Attention
相较于直接对 d m o d e l d_{model} dmodel维度的keys、values以及queries进行一个attention,Transformer则是使用了不同的、可学习的线性映射,对keys、values以及queries线进行一次投影,然后再进行attention,并且该过程会进行 h h h次,最后将这 h h h次的结果进行拼接,再送入一个线性层中进行最终输出的产生。Multi-Head Attention使得模型可以从不同的角度去关注信息,具体见下图:

其计算公式为: M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O MultiHead(Q,K,V)=Concat(head_1,...,head_h)W^O MultiHead(Q,K,V)=Concat(head1,...,headh)WO其中 W i Q ∈ R d model × d k , W i K ∈ R d model × d k , W i V ∈ R d model × d v , W O ∈ R h d v × d model W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}},W^{O} \in \mathbb{R}^{h d_{v} \times d_{\text {model }}} WiQ∈Rdmodel ×dk,WiK∈Rdmodel ×dk,WiV∈Rdmodel ×dv,WO∈Rhdv×dmodel .
在Transformer的实现中,head的数目 h h h设置为8,对于每个head有: d k = d v = d m o d e l / h = 512 / 8 = 64 d_k=d_v=d_{model}/h=512/8=64 dk=dv=dmodel/h=512/8=64.
4.2.3 Applications of Attention in Transformer
Muti-Head Attention的使用位置:
- Encoder-Decoder Attention:queries来自之前的Decoder layer,keys和values来自Encoder的输出,对应于Transformer结构图中Decoder的中间的Multi-Head Attention。
- Self-Attention:queries、keys以及values均来自与前一个Encoder的output,对应于Transformer结构图中Encoder的MultiHeadAttention。
- Self-Attention:queries、keys以及values均来自与当前序列的真值,不过该真值会通过mask对当前时间t以后的结果进行mask out,对应于Transformer结构图中Decoder的Masked Multi-Head Attention。
4.3 Position-wise Feed-Forward Networks
Transformer中的主要参数则是来源于FFN部分。
FFN包含两个全连接网络,中间接一个ReLU激活函数,不同layer之间FFN不共享参数,也可以使用两个1*1卷积去替换。
F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2FFN的特征个数变化为: d m o d e l = 512 → d f f = 2048 → d m o d e l = 512 d_{model}=512 \rightarrow d_{ff}=2048 \rightarrow d_{model}=512 dmodel=512→dff=2048→dmodel=512,即先升维再降维。
4.4 Positional Encoding
由于Transformer本身的结构是无法获取位置信息的,其具有Permutation-Invariant,该特性的推导可以参加我的另一篇博客:2021-Conditional Positional Encodings for Vision Transformers。
为了使得模型可以利用上序列的顺序信息,Transformer对于Input Embeddings额外加上了一个Positional Encodings。Positional Encodings具有与Input Embedding一样的维度,以便于对两者进行相加。
Positional Encodings通常有可学习的或者固定的两种方式,而在本文中其采用的是固定的Positional Encodings的方式:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d model ) P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d model ) \begin{array}{r} P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \end{array} PE(pos,2i)=sin(pos/100002i/dmodel )PE(pos,2i+1)=cos(pos/100002i/dmodel )
其中 p o s pos pos是表示的是位置,而 i i i则是维度。也就是说对于一个序列来说,实际上会生成一个二维的位置编码,即每个token(位置 p o s pos pos)的embedding vector的每个索引位置(维度 i i i)都会有其独一无二的Positional Encoding的值。
作者这么设计的原因是考虑到在NLP任务中,除了单词的绝对位置,单词的相对位置也非常重要。根据公式 s i n ( α + β ) = s i n α c o s β + c o s α s i n β sin(\alpha+\beta)=sin\alpha cos\beta + cos\alpha sin\beta sin(α+β)=sinαcosβ+cosαsinβ, c o s ( α + β ) = c o s α c o s β − s i n α s i n β cos(\alpha+\beta)=cos\alpha cos\beta - sin\alpha sin\beta cos(α+β)=cosαcosβ−sinαsinβ,这表明位置 k + p k+p k+p的位置向量可以表示为位置 k k k的特征向量的线性变化,这为模型捕捉单词之间的相对位置关系提供了非常大的便利。
5. Evaluation
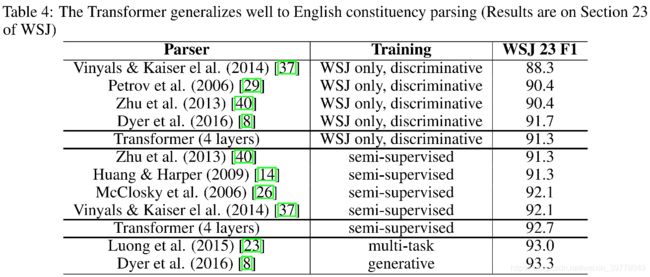
Transformer取得了超越之前集成模型的精度,训练的成本也低了很多。

6. Conclusion
作者在本文中首次提出了一个完全基于Attention机制的序列翻译模型,相较于RNN或者是CNN,其捕获远距离依赖的效率更高;其基于Embedding的机制,也使得其对多模态数据的处理更为方便。