【深度学习】01-04-深度学习(选修)-李宏毅老师21&22深度学习课程笔记
01-04-深度学习(选修)
- Introduction
-
- Deep learning attracts lots of attention
- Ups and downs of Deep Learning
- Neural Network
- Three Steps for Deep Learning
-
- Define A Function Set
- Goodness of Function
-
- Loss Function
- Gradient Descent
- The Best Function
- Fully Connect Feedfroward Network
-
- Define A Function Set
- Gradient Descent
-
- The Best Function
- Matrix Operation
- Example Application - Handwriting Digit Recognition
- FAQ
-
- How many layers? How many neurons for each layer?
- Can the structure be automatically determined?
- Can we design the network structure?
- Concluding Remarks
-
- What are the benefits of deep architecture?
-
- Deeper is Better?
- Useful Links
- Backpropagation
-
- What is Backpropagation?
- What's the principle?
-
- Chain Rule
- Loss Function And Gradient
- Forward Pass
- Backward Pass
-
- Case 1 Output is Network Output
- Case 2 Output is Not Network Output
- Summary
- Example Application(Regression)
-
- Step 1 : Model
- Step2 : Goodness of Function
-
- Training Data
- Loss Function
- Step3 : Best Function
-
- Gradient Descent
-
- Case 1 : One Parameter
- Case 2 : Two Parameters
- How's the results?
-
- Average Error on Training Data
- Average Error on Testing Data
- How can we do better?
-
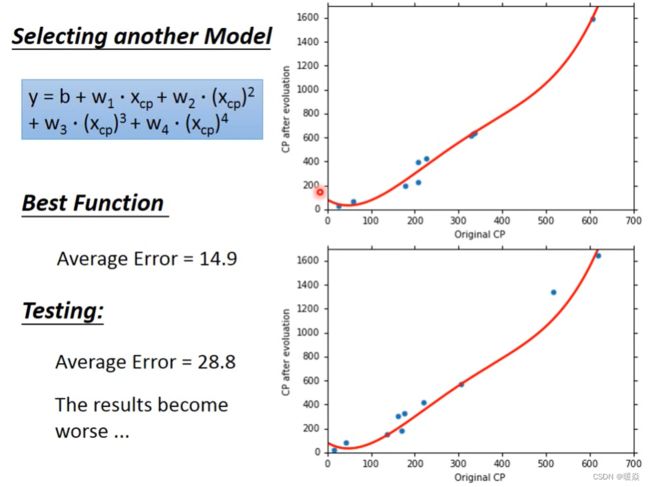
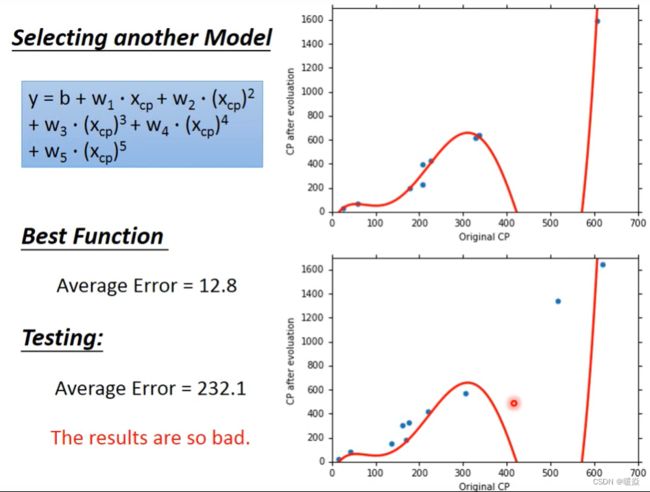
- Selecting another Model
-
- Overfitting
- Let's collect more data
-
- What are the hidden factors?
-
- Species
- Any other hidden factors
- Regularization
-
- Why the functions with smaller Wi are better?
- Why smooth functions are preferred?
- How smooth?
- Conclusion & Following Lectures
- Example Application(Classification)
-
- Question
- How to do Classification
-
- Classification as Regression?
- Ideal Alternatives
- Prior Probability & Conditional Probability & Posterior Probability
- Generative Model
- Gaussian Distribution
- How to find out the Gaussian distribution of the total sample
-
- Maximum Likelihood
- How to do Classification?
- How to improve the correct rate?
- Posterior Probability
- How about directly find w and b?
- Logistic Regression
-
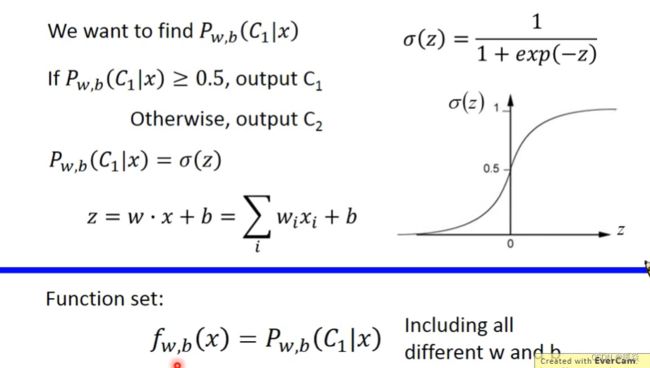
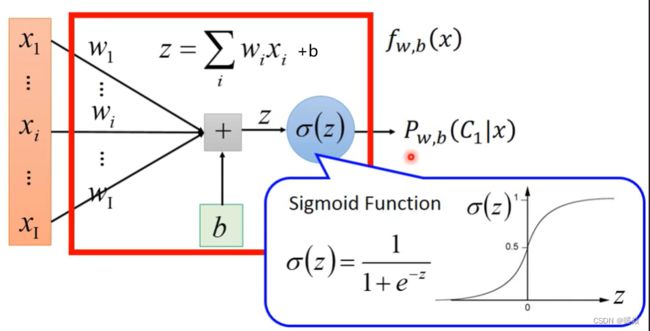
- Step 1 : Function Set
- Step2 : Goodness of a Function
-
- Cross Entropy (Between Two Bernoulli Distribution)
- Step3 : Find The Best Function
- Limitation of Logistic Regression
-
- Feature Transformation
-
- Find a Good Transformation (Cascading Logistic Regression Models)
- Logistic Regression Vs Linear Regression
- Discriminative Vs Generative
-
- Example
-
- Generative(Naive Beyes)
- Multi-class Classification(3 classes as example)
-
- Softmax
Introduction
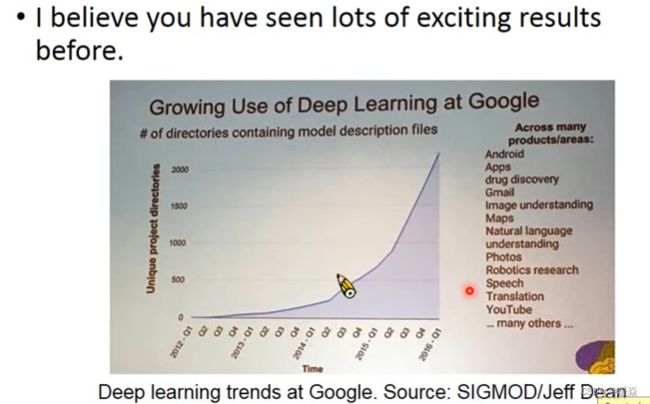
Deep learning attracts lots of attention
Ups and downs of Deep Learning
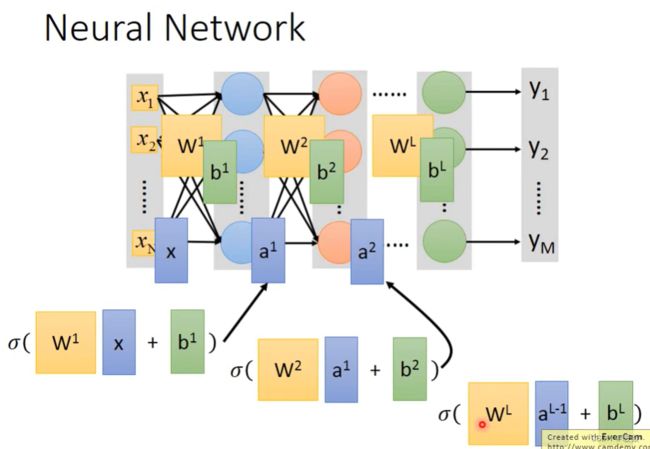
Neural Network
传统机器学习其实和深度学习非常相似,面临的问题从自己定义function set换成了自己设计神经网络的架构。
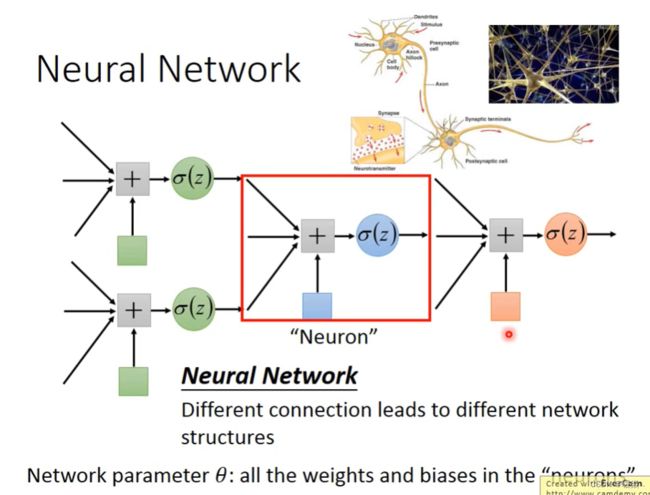
神经网络的特点是它可以包含以前的linear model无法包含的function,因为它的function set很大,能表达出以前不能表达的情况。
神经网络通过隐藏层提取特征,替代了传统机器学习中的特征工程(即手动选择特征),在隐藏层最后一层输出的就是新的特征,而输出层就拿着这些新的特征作为输入,通过一个多分类器(softmax函数),得到最后输出 y。
神经网络可以自动进行特征提取,但是也要面临新的问题,需要人为设计隐藏层层数和每层的神经元个数。对于cv和nlp领域的问题来说,设计神经网络相比找寻特征更为容易,所以神经网络在这两个领域得到了充分的应用。
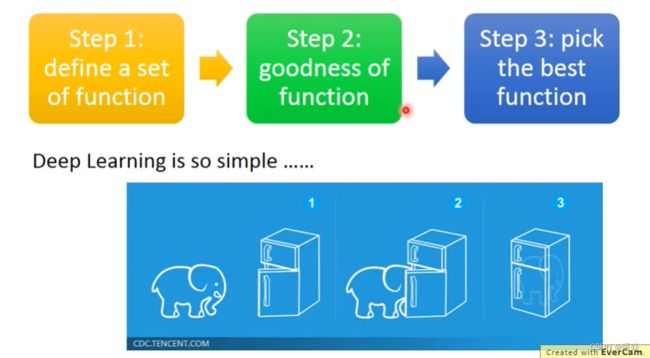
Three Steps for Deep Learning
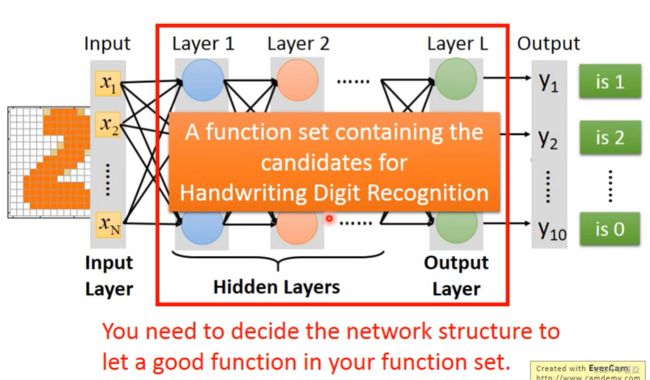
Define A Function Set
Given network structure, define a function set.
只设计出神经网络的结构,参数都是未知的。
如果定义出的网络框架结构设置不同的参数,就会得到不同的 function,把所有可能的 function 统称为function set。
Goodness of Function
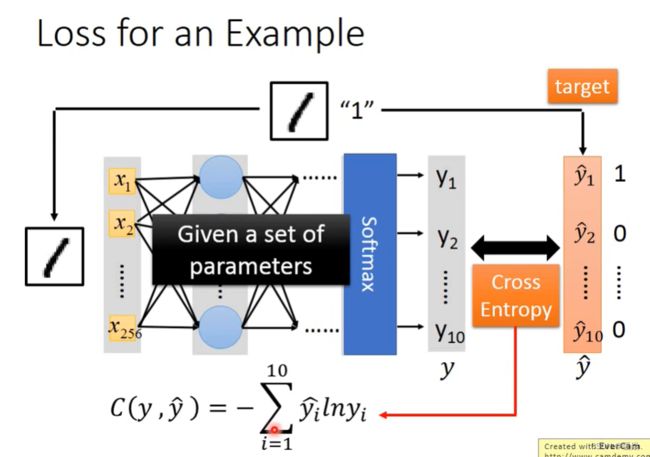
Loss Function
Gradient Descent
给出一组参数初始值,使用 Gradient Descent 梯度下降算法,最小化损失。


The Best Function
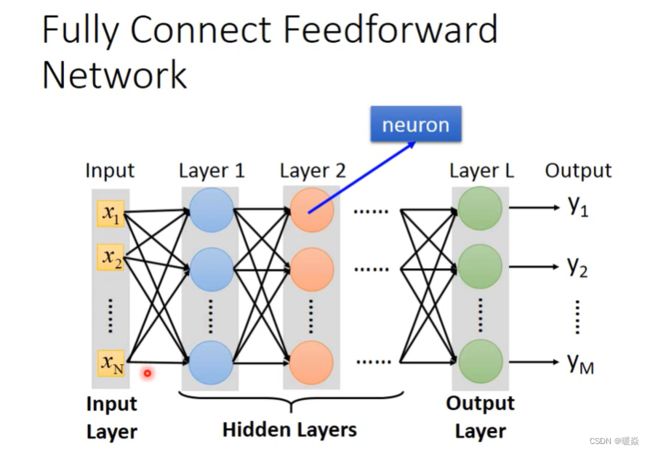
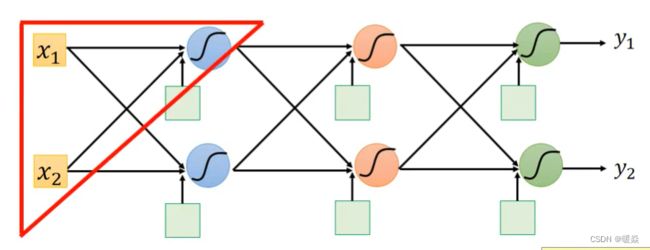
Fully Connect Feedfroward Network
全连接:后一层每一个神经元与前一层的所有神经元都互相连接。
前馈 : 传递方向是由从前往后传递。
Define A Function Set
Given network structure, define a function set.
只定义出了网络的结构,参数都是未知的。
如果定义出的网络框架结构设置不同的参数,就会得到不同的 function,把所有可能的 function 统称为function set。
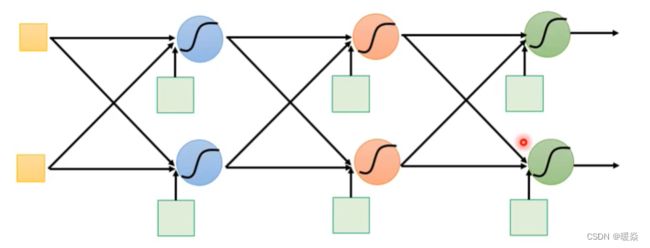
定义一个好的网络框架结构很重要,这决定了function set中的function的好坏,后续需要从function set中寻找一个效果最好的function。
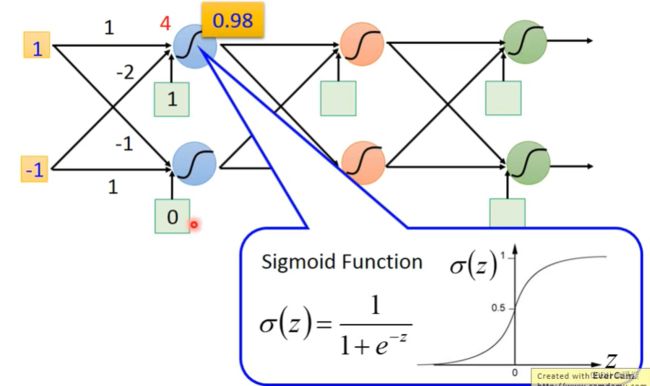
Gradient Descent
如果知道所有的参数(weight, bias),就可以计算出输出结果。
The Best Function
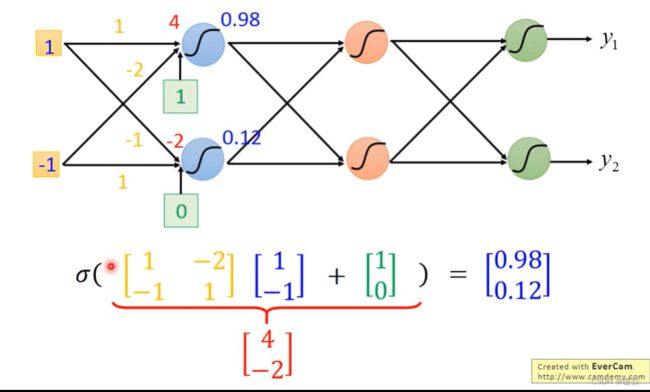
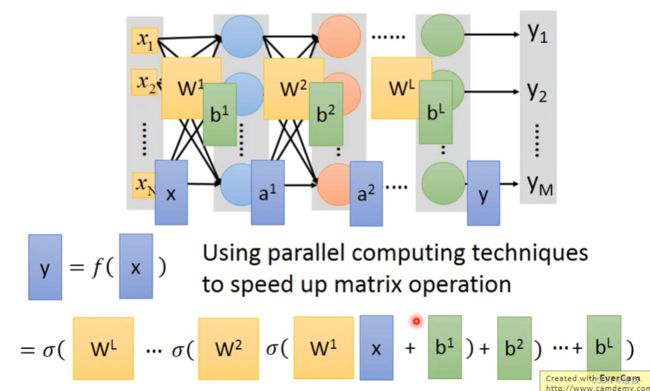
Matrix Operation
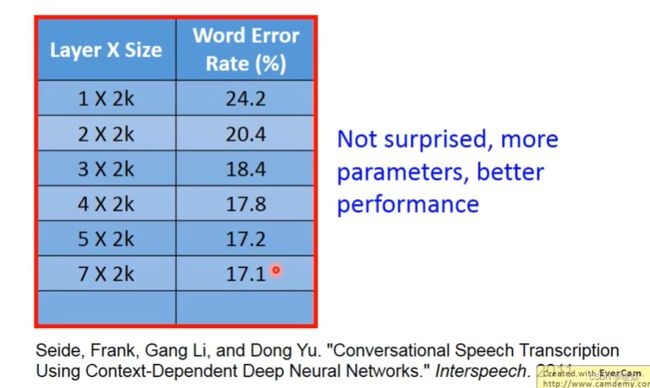
层数越多,错误率越低,但运算量越大,通常都是超过亿万级的计算。对于这样复杂的结构,一定不能使用CPU一个一个的计算。所以为了提高效率,引入矩阵运算,并使用GPU计算。
上例中矩阵运算过程:
[ 1 − 2 − 1 1 ] [ 1 − 1 ] + [ 1 0 ] = 1 [ 1 − 1 ] + ( − 1 ) [ − 2 1 ] + [ 1 0 ] = [ 4 − 2 ] \begin{bmatrix} 1 & -2 \\ -1 & 1\\ \end{bmatrix} \begin{bmatrix} 1 \\ -1 \\ \end{bmatrix}+ \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} =1 \begin{bmatrix} 1 \\ -1 \\ \end{bmatrix} +(-1) \begin{bmatrix} -2 \\ 1 \\ \end{bmatrix} +\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}= \begin{bmatrix} 4 \\ -2 \\ \end{bmatrix} [1−1−21][1−1]+[10]=1[1−1]+(−1)[−21]+[10]=[4−2]
扩展知识:矩阵与向量乘法
本质:线性变换作用于给定向量
[ a b c d ] [ x y ] = x [ a c ] + y [ b d ] = [ a x + b y c x + d y ] \begin{bmatrix} a & b \\ c & d\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} =x \begin{bmatrix} a \\ c \\ \end{bmatrix} +y \begin{bmatrix} b \\ d \\ \end{bmatrix}= \begin{bmatrix} ax+by \\ cx+dy \\ \end{bmatrix} [acbd][xy]=x[ac]+y[bd]=[ax+bycx+dy]
矩阵与向量乘法可以解读为:线性变换作用于给定向量的一种途径。
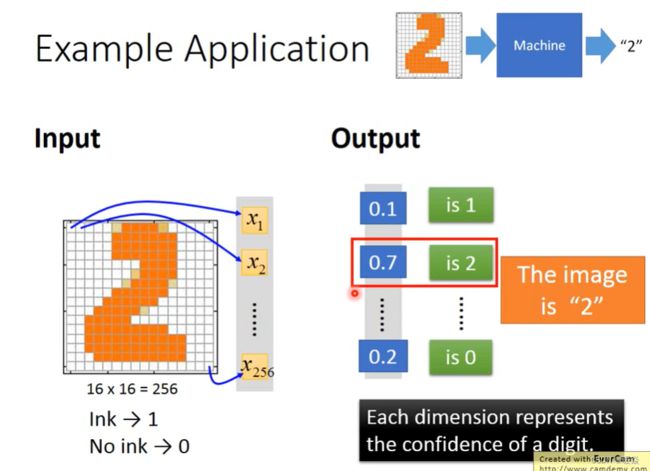
Example Application - Handwriting Digit Recognition
输入:是一张图片,假设是16x16的图片,那么输入是一个256维度的向量。每个pixel对应一个dimension,有颜色用(ink)用1表示,没有颜色(no ink)用0表示。
输出:10个维度,每个维度代表一个数字的置信度(属于某个数字的概率),所有类别中概率最大的是数字 2 概率 0.7,这说明图片中是数字2的可能性最大。

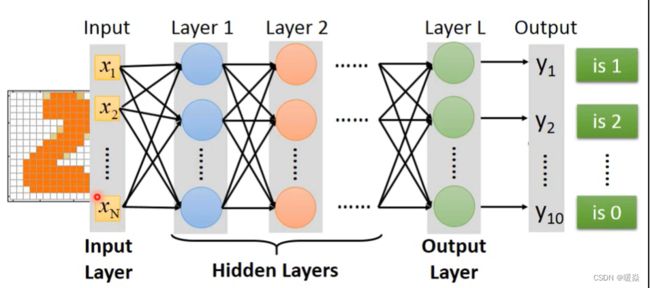
神经网络需要自己决定layer层数,每一层neuron神经元个数,即这个神经网络的结构,神经网络的结构决定了函数集(function set)。
FAQ
How many layers? How many neurons for each layer?
Trial and Error + Intuition
只能不断尝试+直觉的方法来进行调试。
Can the structure be automatically determined?
现在有技术可以实现神经网络自动设计,不需要认为设计。
E.g. Evolutionary Artificial Neural Networks
Can we design the network structure?
E.g. Convolutional Neural Network (CNN)
Concluding Remarks
What are the benefits of deep architecture?
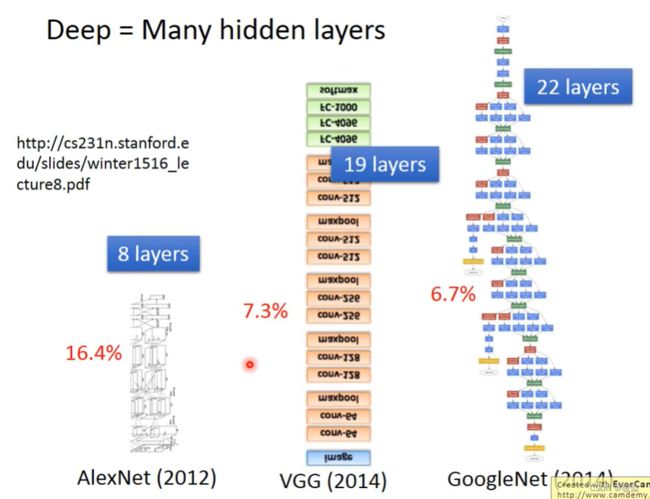
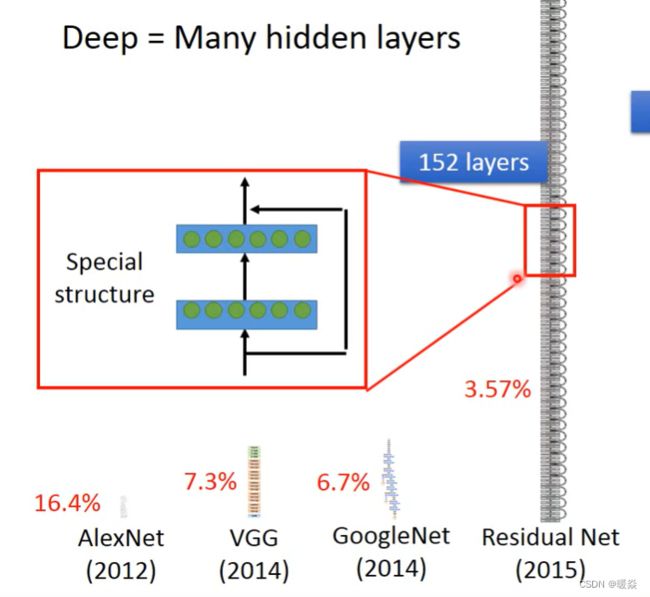
Deeper is Better?
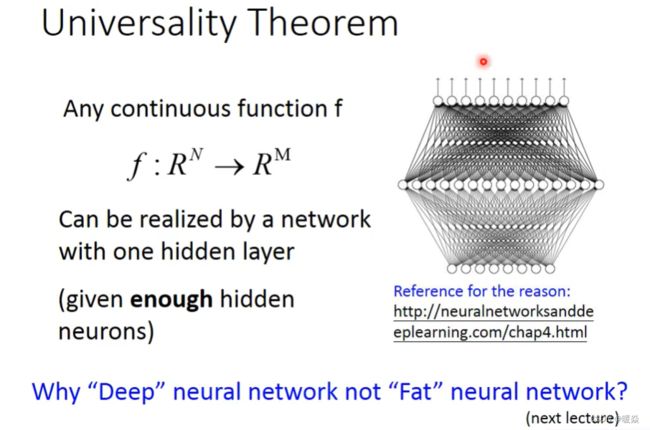
这里有一个通用的理论:对于任何一个连续的函数,都可以用足够多神经元的一个隐藏层来表示。
问题:既然一个隐藏层就可以表示任何连续函数,为什么还要追求深度?deeper是否真的有用?
Useful Links
My Course: Machine learning and having it deep and structured
http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLSD15_2.html
6 hour version 李宏毅tutorial : http://www.slideshare.net/tw_dsconf/ss62245351
“Neural Networks and Deep Learning"
written by Michael Nielsen
http://neuralnetworksanddeeplearning.com/
“Deep Learning”
written by Yoshua Bengio , Ian J. Goodfellow and Aaron Courville
http://www.deeplearningbook.org
Backpropagation
What is Backpropagation?
相比机器学习,神经网络中参数非常多,Backpropagation 是实现 Gradient Descent 的一种方式,使得 Neural Network 中的梯度下降算法更简单高效。

What’s the principle?
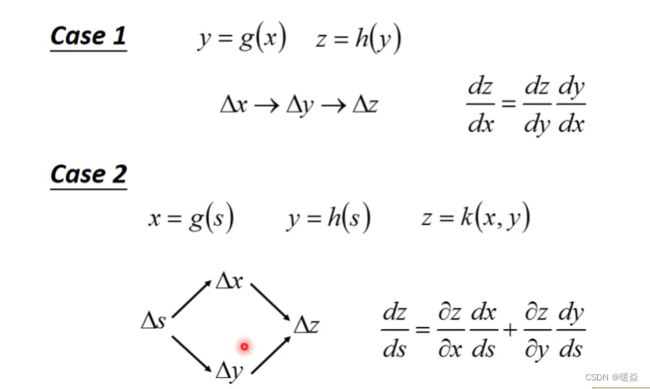
Chain Rule
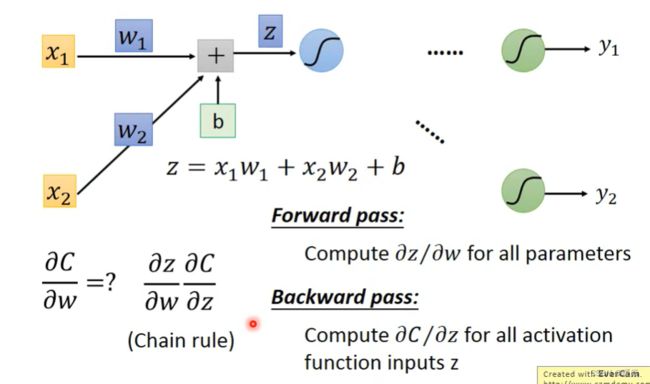
Loss Function And Gradient
梯度下降的本质是计算损失函数对参数的梯度,先考虑单个 C i ( θ ) C^{i}(\theta) Ci(θ)对w的导数。
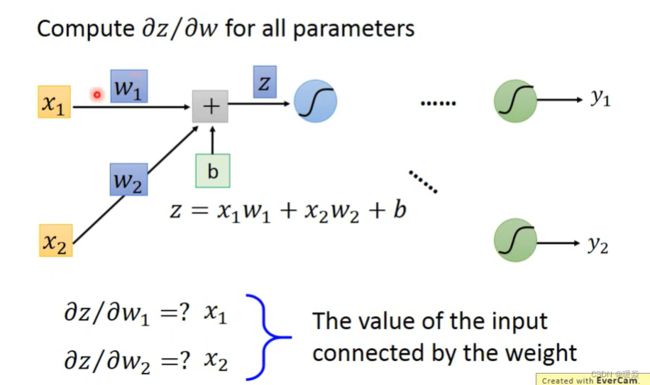
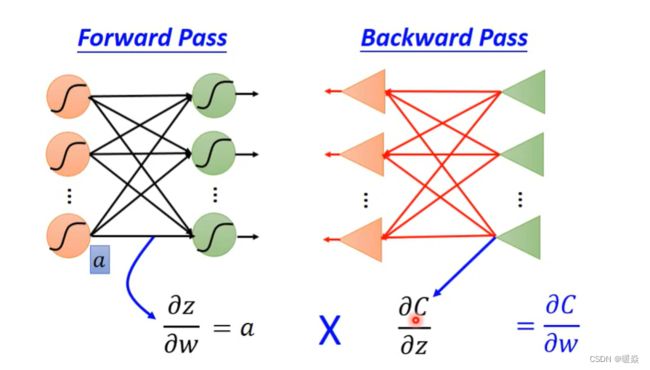
Forward Pass
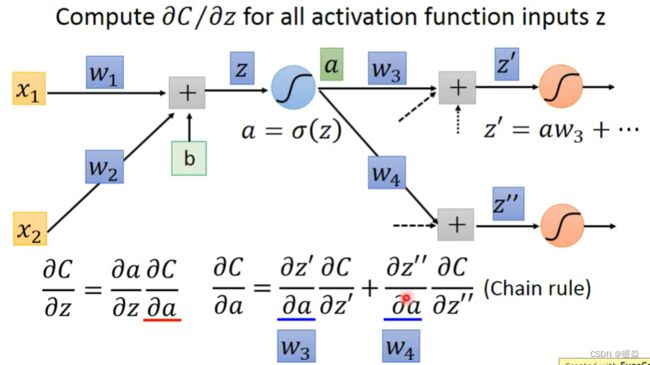
Backward Pass
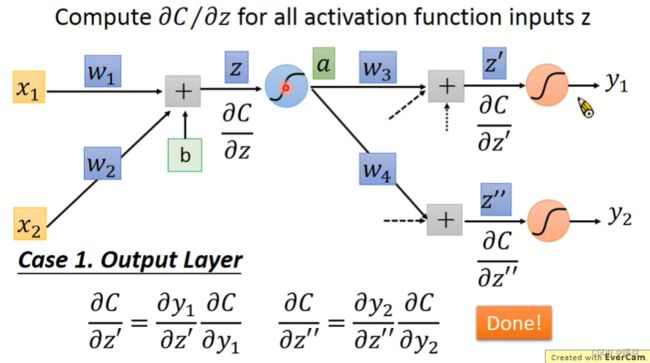
Case 1 Output is Network Output
y1 和 y2 就是输出。
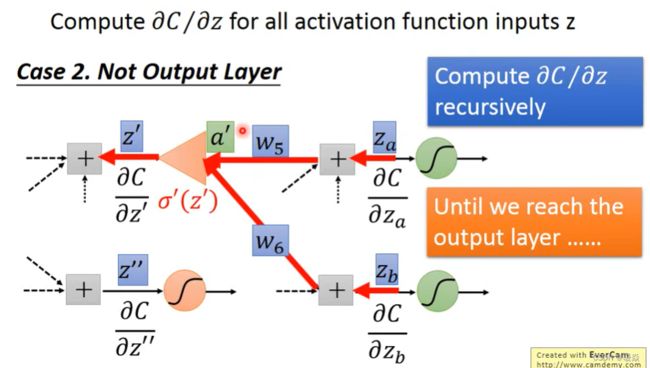
Case 2 Output is Not Network Output
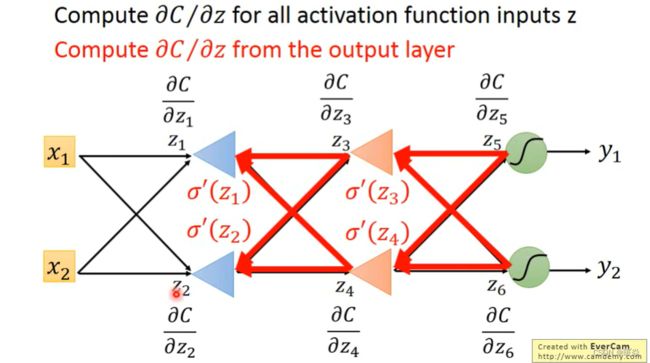
Summary
Example Application(Regression)
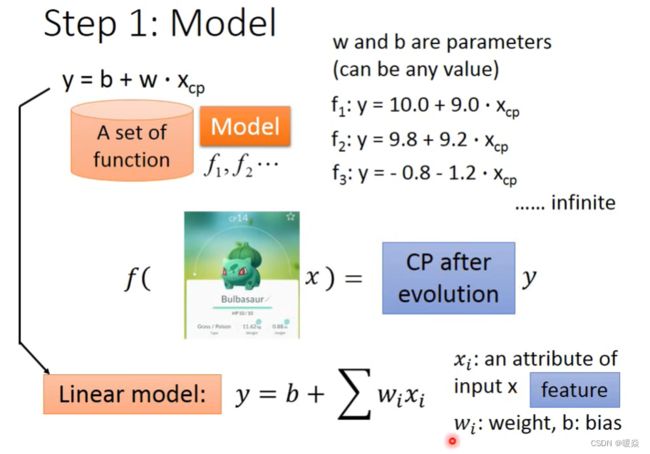
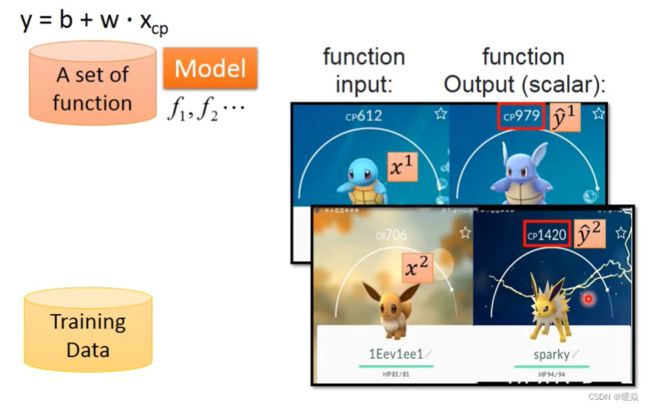
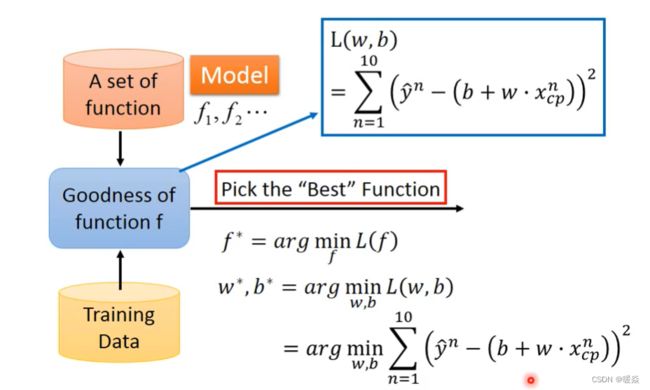
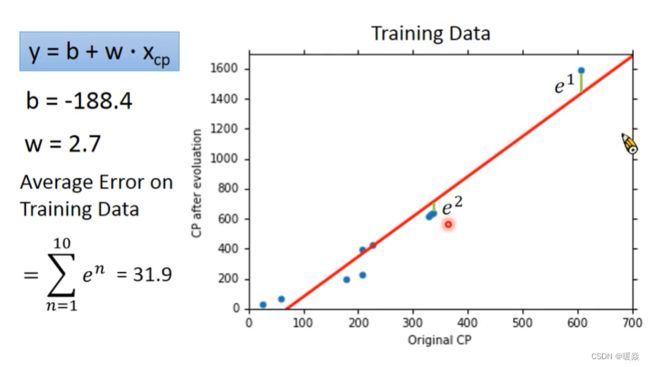
Step 1 : Model
Step2 : Goodness of Function
Training Data
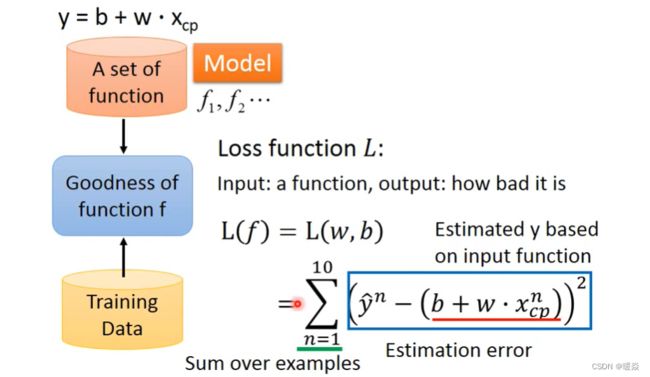
Loss Function
Step3 : Best Function
Gradient Descent
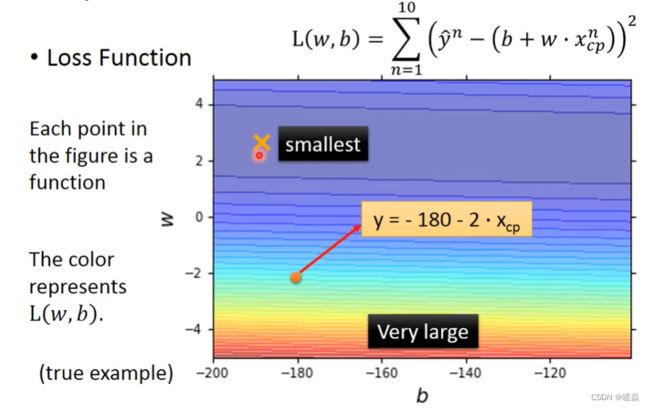
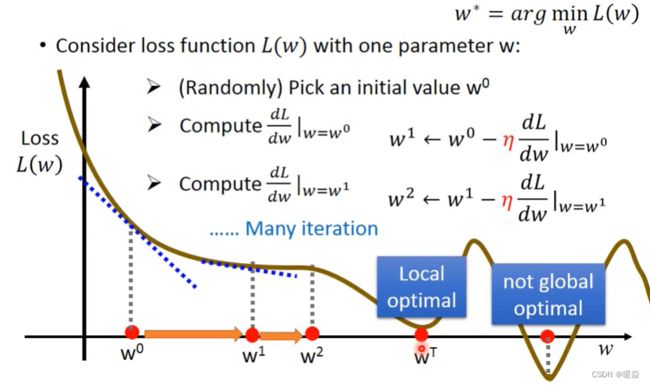
Case 1 : One Parameter
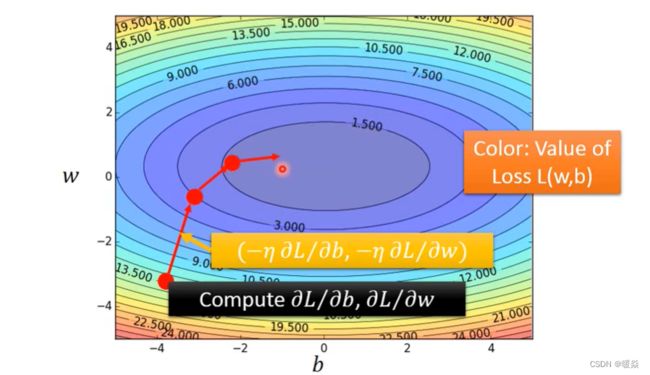
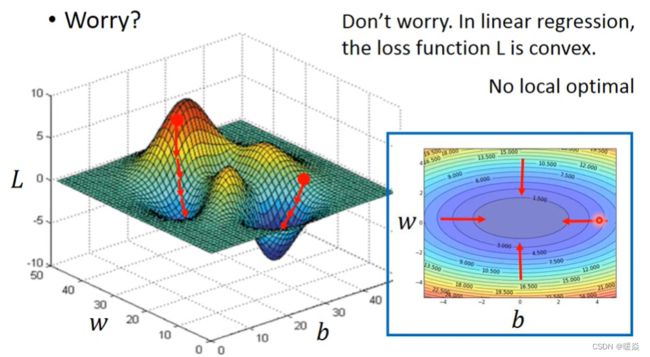
Case 2 : Two Parameters
How’s the results?
Average Error on Training Data
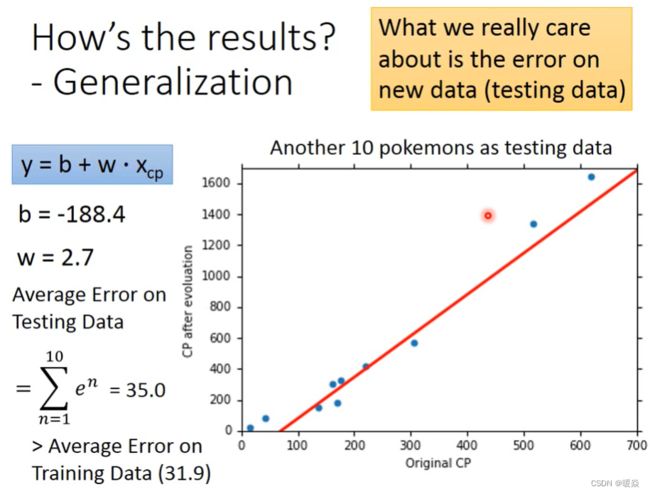
Average Error on Testing Data
从图像中看出,在测试数据上,Original CP偏小或偏大的地方误差较大。
How can we do better?
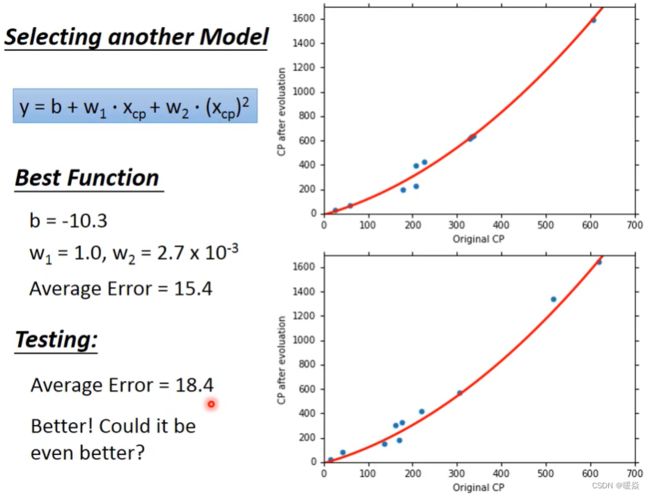
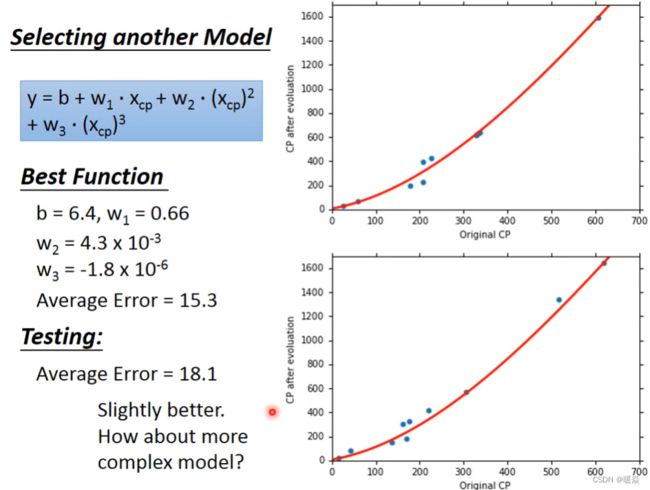
Selecting another Model
Overfitting
Let’s collect more data
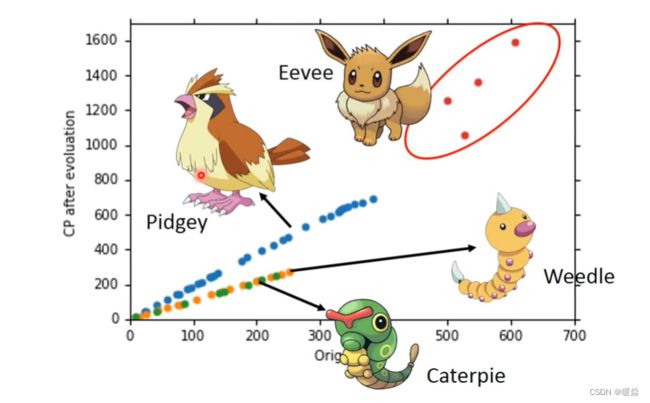
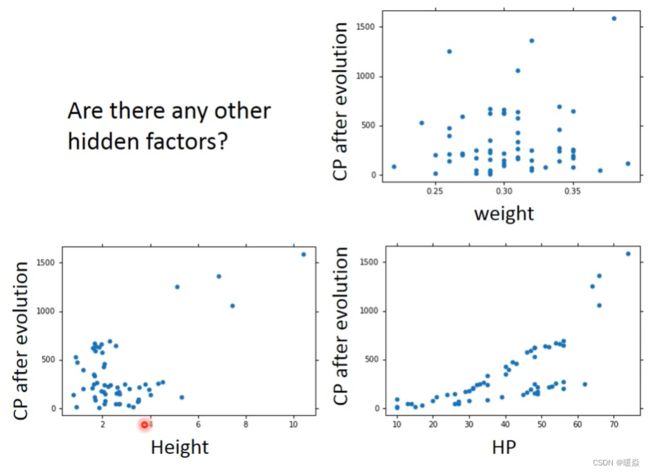
What are the hidden factors?
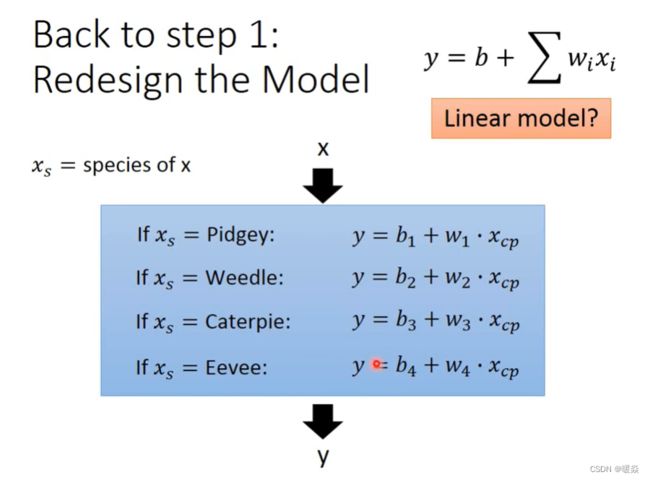
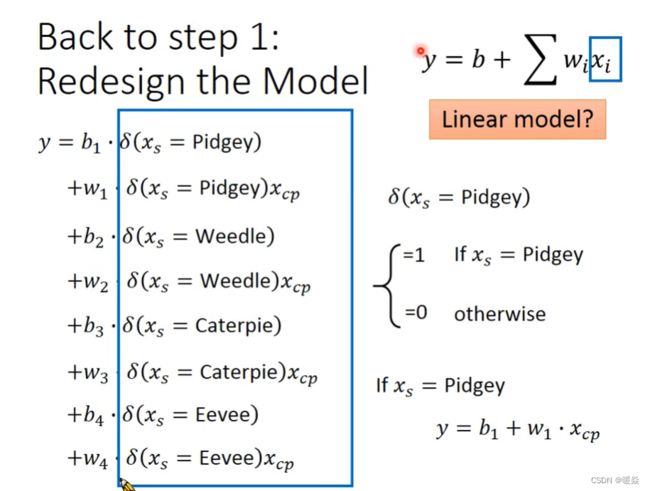
Species
考虑物种差异之后的模型,也是Linear Model。
![]()
Any other hidden factors
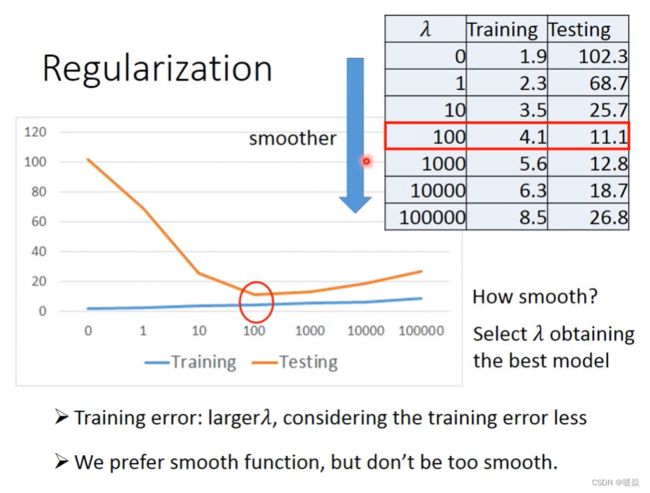
Regularization
正则项中一般不考虑偏置项 b 。
Why the functions with smaller Wi are better?
Wi 越小,function 曲线越平滑。
Why smooth functions are preferred?
Wi越小,function 曲线越平滑,Xi的改变将会使得Y的变化更不敏感。
If some noises corrupt input Xi when testing, a smoother function has less influence.
How smooth?
Conclusion & Following Lectures
问题:如果将这个模型放到网上,提供给更多人使用,得到的错误率是高还是低?为什么?
Example Application(Classification)
Question
问题是找到一个Function,输入是一只随机的宝可梦,输出是这只宝可梦属于哪一种类型。例如,输入是皮卡丘,输出就是雷属性。输入是杰尼龟,输出就是水属性。输入是妙蛙草,输出就是草属性。现在暂定宝可梦类型有18种,如下图所示。

现在的问题是怎样把一只宝可梦作为输入,所以需要考虑到输入的数值化。宝可梦有很多属性,这些属性都可以用数字表示。例如综合能力,生命值,攻击力,防御力,特殊攻击力,特殊防御力,速度。

宝可梦在战斗中存在属性相克的情况,因此问题在于当对方给出没有出现过的宝可梦时,我们需要使用Function预测出宝可梦的种类,并且选择出最有利属性的宝可梦去战斗。
How to do Classification
Classification as Regression?
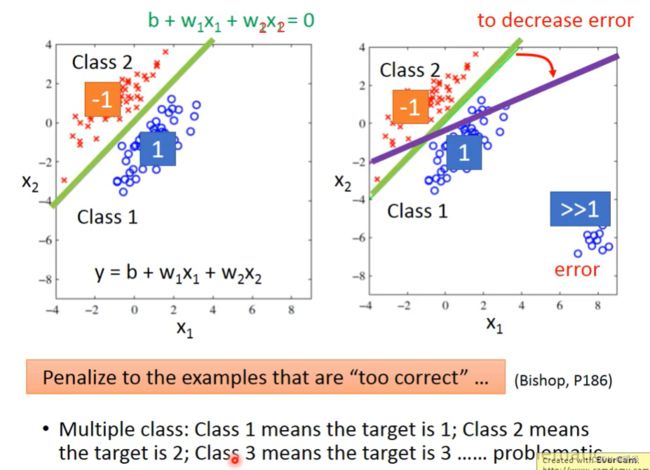
假设Classification问题中只有两种分类,如果将 Classification 当做 Regression,按照 Regression 的思路解决,预测值接近1时为class 1,预测值接近-1时为 class 2,该情形下,会面临两个问题:
1 上图中右图所示,如果存在预测值远大于1的样本,预测分界线将因为要满足这些样本而发生倾斜,但是这种倾斜会导致错误率上升。
2 上述情况,默认了class 2和class 1比较接近,class 3和class 2比较接近,这种默认可能与实际问题不符合。
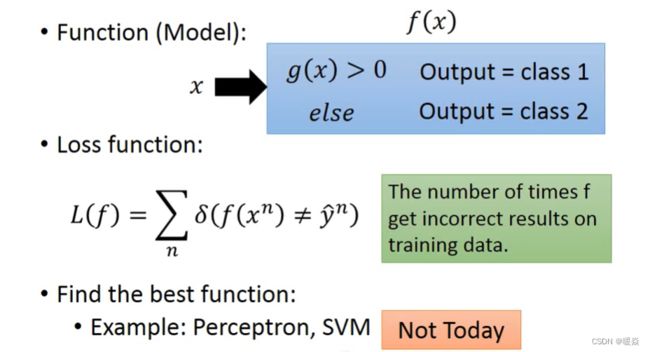
Ideal Alternatives
解决该分类问题,理想的Model是输出为0,则为分类1,输出为1,则为分类2。能做到这种效果的方法有很多中,例如:Perceptron,SVM,但今天讨论另外一种方法:Generative Model。
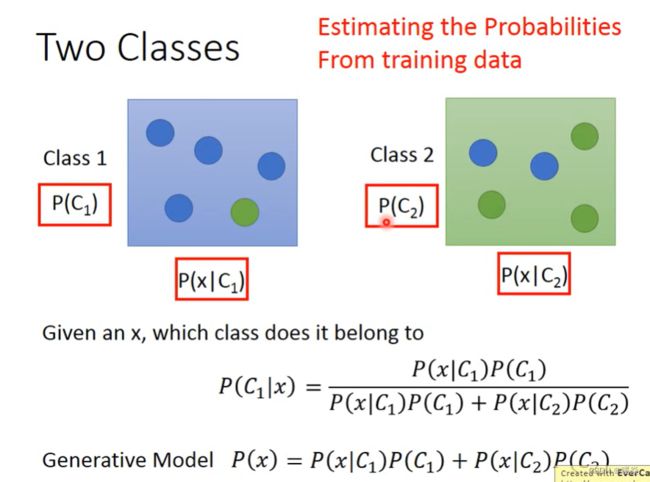
Prior Probability & Conditional Probability & Posterior Probability
为了很好的说明这个问题,在这里举一个例子:
玩英雄联盟占到中国总人口的60%,不玩英雄联盟的人数占到40%:
为了便于数学叙述,这里我们用变量X来表示取值情况,根据概率的定义以及加法原则,我们可以写出如下表达式:
P(X=玩lol)=0.6;P(X=不玩lol)=0.4,这个概率是统计得到的,或者你自身依据经验给出的一个概率值,我们称其为先验概率(prior probability);
另外玩lol中80%是男性,20%是小姐姐,不玩lol中20%是男性,80%是小姐姐,这里我用离散变量Y表示性别取值,同时写出相应的**条件概率(conditional probability)**分布:
P(Y=男性|X=玩lol)=0.8,P(Y=小姐姐|X=玩lol)=0.2
P(Y=男性|X=不玩lol)=0.2,P(Y=小姐姐|X=不玩lol)=0.8
那么我想问在已知玩家为男性的情况下,他是lol玩家的概率是多少:
依据贝叶斯准则可得:
P(X=玩lol|Y=男性)=P(Y=男性|X=玩lol)*P(X=玩lol)/
[ P(Y=男性|X=玩lol)*P(X=玩lol)+P(Y=男性|X=不玩lol)*P(X=不玩lol)]
最后算出的P(X=玩lol|Y=男性)称之为X的后验概率(posterior probability),即它获得是在观察到事件Y发生后得到的
先验/条件/后验概率Prior/Conditional/Posterior probability - 身高163的文章 - 知乎
如何理解先验概率与后验概率 - 昌硕的文章 - 知乎
Generative Model
假设训练样本集服从某种概率分布,求产生该训练样本集可能性最大的该种概率分布的均值和方法(最大似然估计),之后,将均值和方差表示该概率分布的概率密度函数,根据贝叶斯公式求该训练样本集中某一个样本出现的概率,概率大于阈值为分类1,概率小于阈值为分类2。

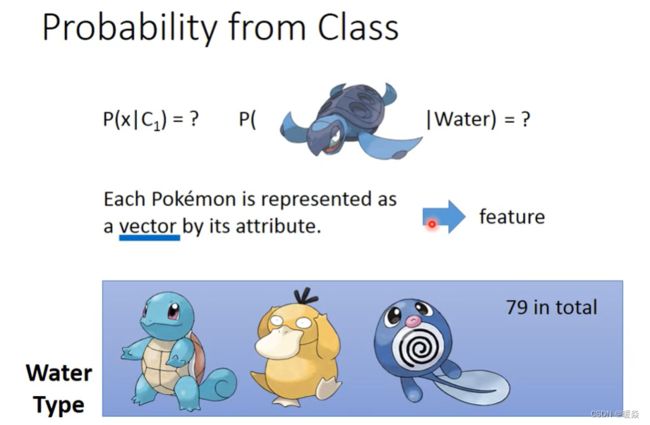
海龟并不是训练样本中已知的数据,但并不代表从水系类中抽出一个宝贝是海龟的概率为0,对于这个问题,可以看做训练样本是从很大的总样本集中抽出的,并且总样本集服从一定的概率分布。
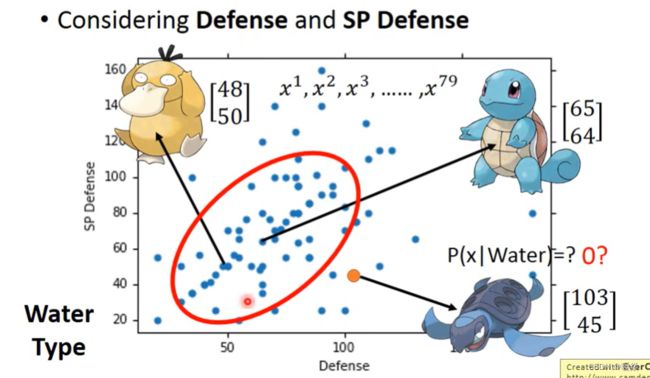
Assume the points are sampled from a Gaussian distribution.
如何从训练样本的分布推算出总样本的分布?
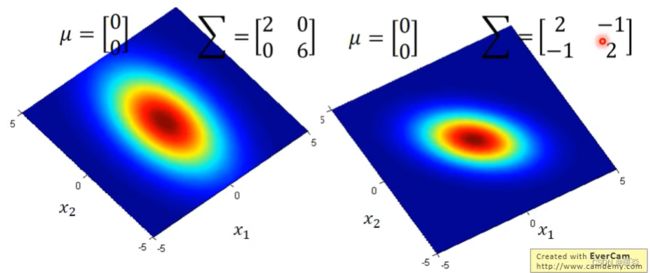
Gaussian Distribution
How to find out the Gaussian distribution of the total sample
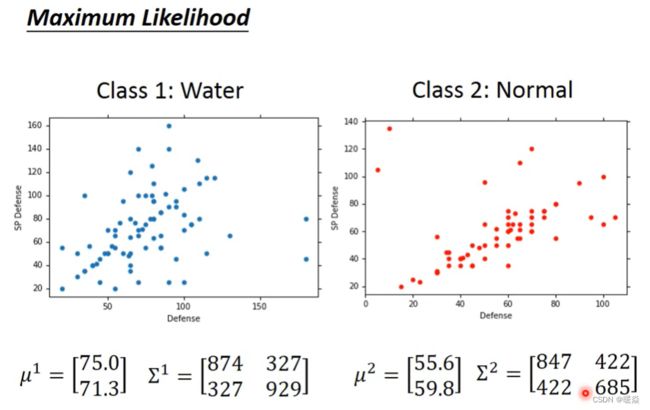
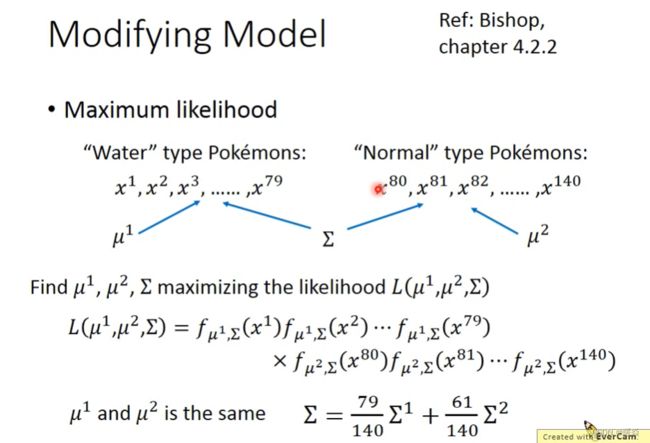
Maximum Likelihood
这79个训练样本可以从不同均值μ和不同协方差矩阵Σ的不同高斯分布中取样,但是从下图中可以看出圆形高斯分布取样出来的样本的likehood比椭圆的高斯分布大,因此应该计算不同高斯分布对79个训练样本的likehood,然后取最大值,就可以找到Maximum Likelihood。
高斯分布的似然值表示该高斯分布产生出当前训练样本的可能性多大。
因此,想要找到产生当前训练样本可能性最大的高斯分布,就等于,寻找最大似然估计值的高斯分布。


宝可梦分类的例子中,假设训练样本服从高斯分布,求最大似然估计,算出最可能产生这些训练样本的高斯分布的均值和方差。
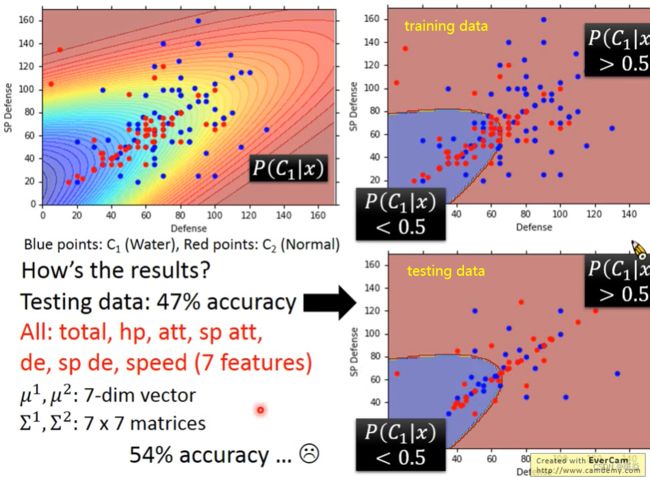
How to do Classification?
How to improve the correct rate?
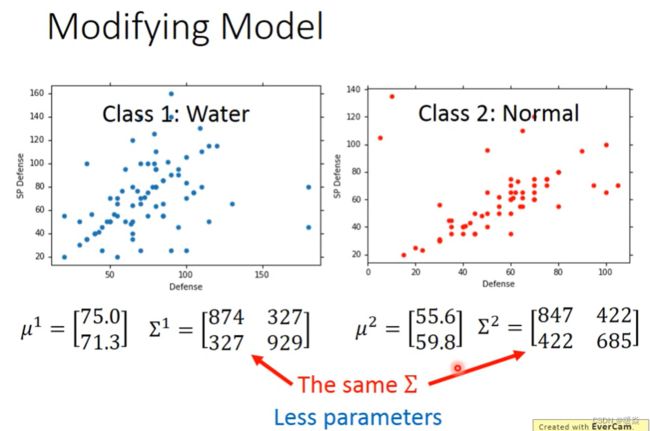
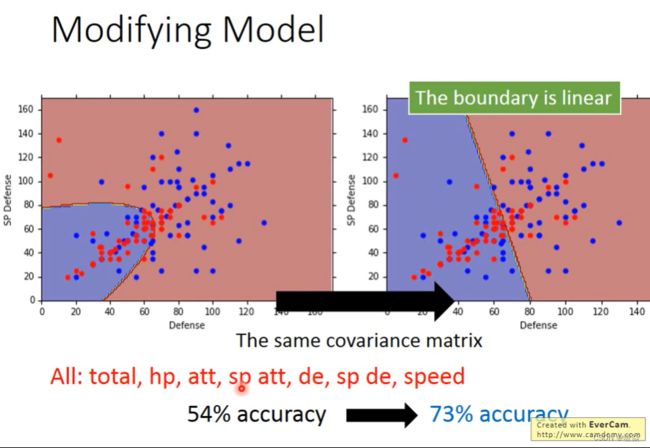
协方差矩阵与特征个数成正比,不同分类使用不同均值不同协方差矩阵的不同高斯分布,参数过多导致过拟合。强制不同分类使用不同均值相同协方差矩阵的不同高斯分布,可以减少参数。
如果样本间独立同分布,可以使得协方差矩阵更简单(对角线非0,其他位置都为0)。
并不是所有的问题都必须假设为高斯分布,视不同问题,可以假设不同的分布,比如二分类的特征,神奇宝贝是不是神兽,只有是或者不是两种分类,则可以假设服从伯努利分布。
Posterior Probability
How about directly find w and b?
问题:为什么要先假设一个概率分布再求均值和协方差而不是直接求w和b?
Logistic Regression
Step 1 : Function Set
Step2 : Goodness of a Function
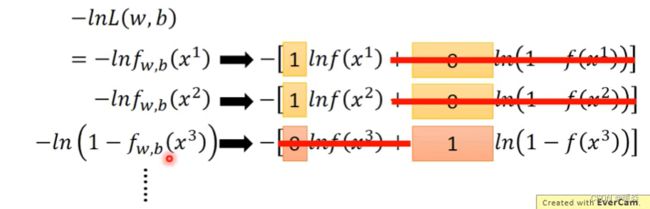
Cross Entropy (Between Two Bernoulli Distribution)
损失函数优化目标:交叉熵越小越好,即两个伯努利分布越接近越好。
Step3 : Find The Best Function
Limitation of Logistic Regression
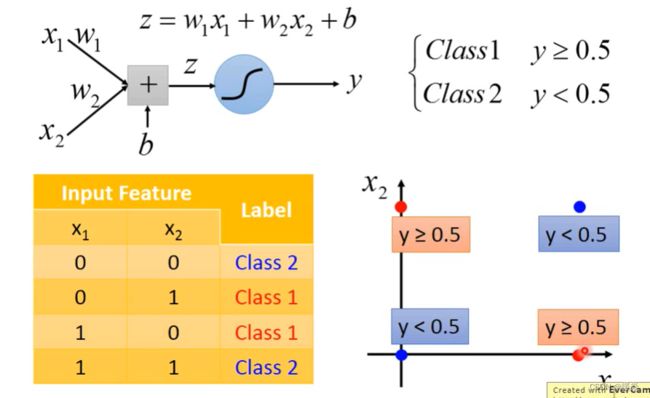
对于以下情况,Logistic Regression 无法得到分类边界,无法对其进行分类。
找一种适合的方式,对样本进行特征转换,使得样本集可以被线性回归找到边界分开。
Feature Transformation
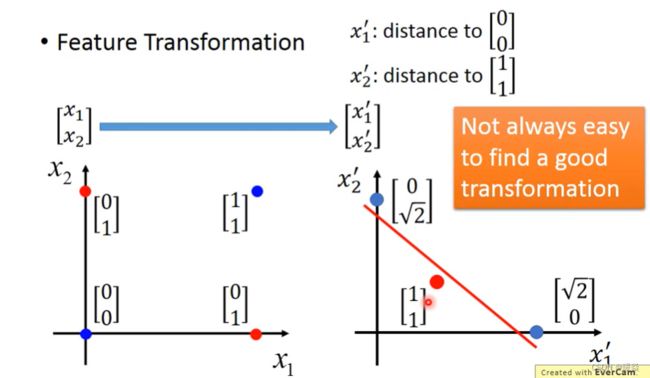
feature transformation特征转换将原始数据投射到另一个feature space上,使其在另一个特征空间中变得线性可分。
对于上面的情况,将 x 1 x_1 x1转换为 x 1 x_1 x1到原点的距离,将 x 2 x_2 x2转换为 x 2 x_2 x2到 (1,1) 点的距离。
Find a Good Transformation (Cascading Logistic Regression Models)
可以通过级联逻辑回归模型实现,即把多个逻辑回归模型连接起来,让机器自己学会特征变换。
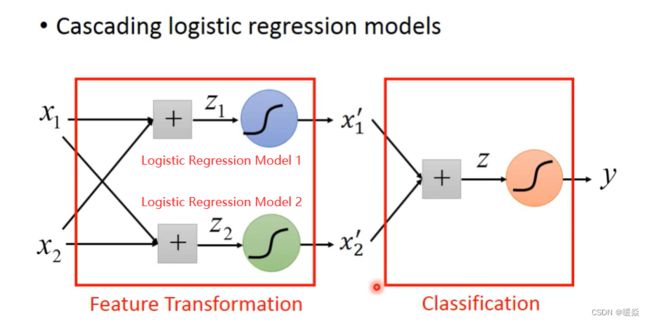
Logistic Regression 的 boundary 一定是一条直线,它可以有任何的画法,但肯定是按照某个方向从高到低的等值线分布,具体的等值线分布可通过调整 Logistic Regression 的参数决定。可以把特征值转化成该样本点到某直线的距离。
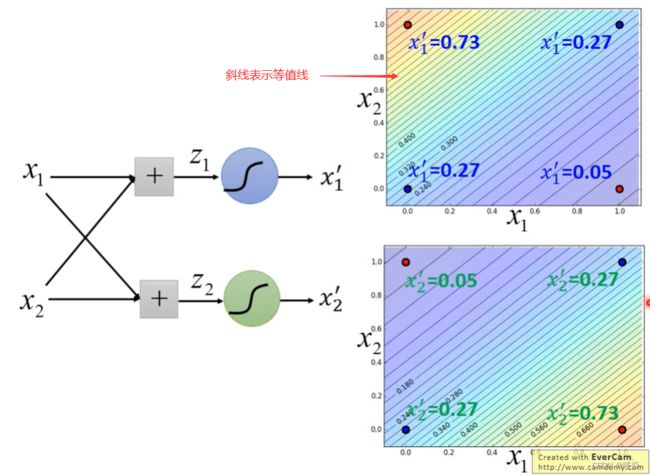
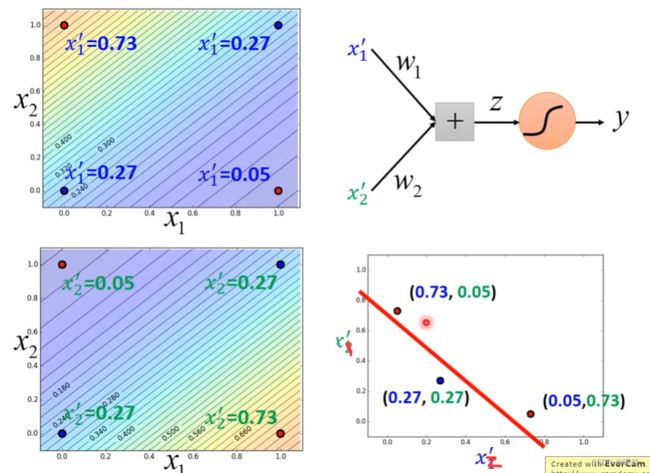
这个例子也说明逻辑回归可以叠加使用,将原始数据投射到另一个feature space上是一轮逻辑回归,找出在另一个特征空间的boundary是第二轮逻辑回归。很多层逻辑回归叠起来也就是deep learning。

Logistic Regression Vs Linear Regression
问题:为什么 Logistic Regression 不使用 Square Errror 作为损失函数?


由上述推导可以看出,当 Logistic Regression 使用 Square Errror 作为损失函数:
离目标近的地方,偏导数小,更新慢。(合理)
离目标远的地方,偏导数也小,更新也慢。(不合理,需要很长时间才能梯度下降到最优点)
并且,也无法区分离目标近还是目标远,无法调节学习率,很难求出最优解。
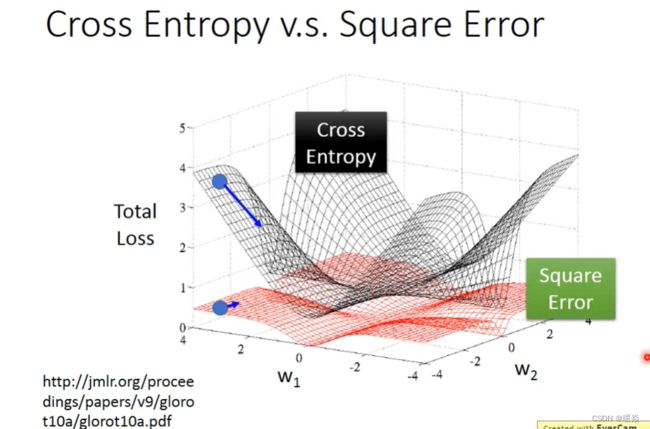
Discriminative Vs Generative
Discriminative Model(判别式模型),Generative Model(生成式模型)。
无论是生成式模型还是判别式模型,都可作为分类器使用,分类器的数学表达即为:给定输入 X 以及分类变量 Y,求 P(Y|X)。
判别式模型直接估算 P(Y|X),或者也可像 SVM 那样,估算出输入和输出之间的映射,与概率无关;判别式模型的典型代表是:logistic 回归;
生成式模型的思想是先估计联合概率密度 P(X,Y),再通过贝叶斯公式求出 P(Y|X);生成式模型的典型代表则是:朴素贝叶斯模型;
一般认为判别式模型更受欢迎,“人们更应该直接去解决问题,永远不要把求解更复杂的问题作为中间阶段”(Vapnik),Andrew Ng 的论文[1]对此作了较为全面的分析,产生式模型(朴素贝叶斯)在少量样本的情况下,可以取得更好的精确率,判别式模型(logistics 回归)在样本增加的情况下,逐渐逼近前者的概率;
Andrew Ng, On Discriminative vs. Generative classifiers: A comparison of logistic regression and naive Bayes
参考:生成式模型和判别式模型的区别 - Cara的文章 - 知乎
生成式模型和判别式模型的模型函数相同,但是求出的最优解可能不同。

Logistic Regression 中没有对样本的分布做任何假设。
Generative 中假设样本的分布为伯努利分布、高斯分布等。
Example
Generative(Naive Beyes)
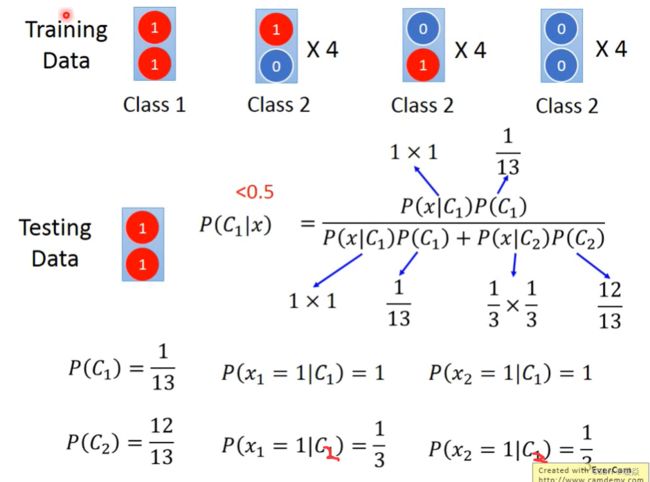
给出testing data,人类直觉应该属于class 1,但是beyes计算出的结果为class 2。
Naive Beyes 不考虑不同 dimension 之间的 correlation,所以Naive Beyes认为Training Data中的class1 两个红色的1是独立产生的,之所以在class 2中没有观测到两个红色的1的样本,是因为样本太少,如果样本足够多,可能就会在class 2中观察到两个红色1的样本。
正因为 Generative Model 对样本的分布进行了假设,所以认为class 2中会出现两个红色1的样本(Generative自己脑补了这种情况)。

1 “脑补”通常不是一件好的事情,因为training data中没有这样的数据,自己假象出来了这种数据。但是,在training data 很少的情况下,效果可能更好。
2 training data 有噪声的情况下,“脑补”可能会使得Generative 受到噪声影响更小。
3 在Generative model中,priors probabilities和class-dependent probabilities是可以拆开来考虑的,以语音辨识为例,现在用的都是neural network,是一个discriminative的方法,但事实上整个语音辨识的系统是一个Generative的system,它的prior probability是某一句话被说出来的几率,而想要estimate某一句话被说出来的几率并不需要有声音的data,可以去互联网上爬取大量文字,就可以计算出某一段文字出现的几率,并不需要声音的data,这个就是language model,而class-dependent的部分才需要声音和文字的配合,这样的处理可以把prior预测地更精确。
Multi-class Classification(3 classes as example)
多元分类问题原理的推导过程与二元分类基本一致, 接下来只讲过程, 不讲原理(原理可参照Bishop的教科书, 简称prml)。
以三个类别C1, C2, C3为例:每一个类别都有自己的weight和bias,输入的向量x是要分类的对象. 输出z1, z2, z3(可以为任意值)。
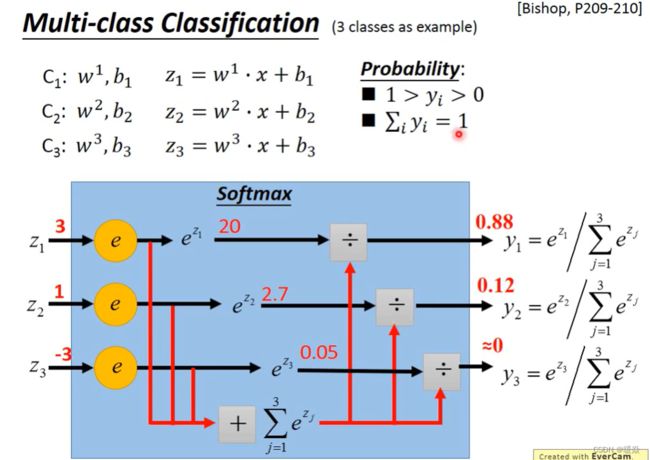
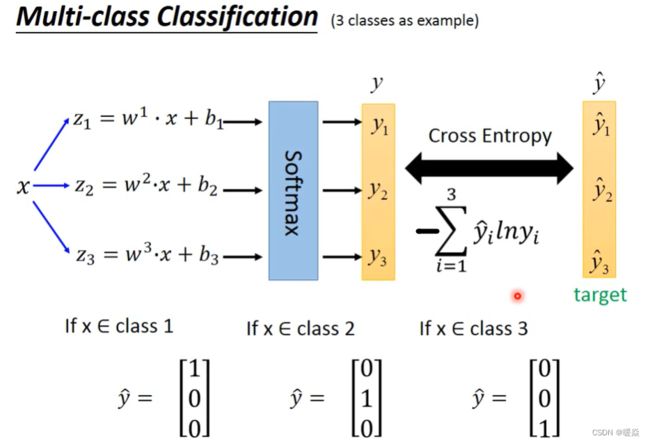
注意:前面提到过,如果设定预测结果为1属于class 1,预测结果为2属于class 2,预测结果为3属于class 3,这样错误的隐含了class 1 与class 2接近,与class 3 差别大的信息,但是类别间并没有这种关系。
Softmax
softmax的作用:对最大值做强化,因为在做第一步的时候,对z取exponential会使大的值和小的值之间的差距被拉得更开,也就是强化大的值。
Softmax公式中为什么要用exp?这是有原因/可解释的,可以看下PRML,也可以搜下最大熵。
最大熵(Maximum Entropy)其实也是一种分类器,和逻辑回归一样,只是从信息论的角度来看待。
输出值y的范围较z发生变化:1 y_i>0, 因为指数e^z>0。2 y_i<1且各类y_i之和为1, 这是归一化的效果。所以softmax的输出可以估计后验概率(posterior probability) P(Y|X)。