机器学习（吴恩达）-Octave/Matlab教程

课程地址：https://study.163.com/course/courseLearn.htm?courseId=1004570029#/learn/video?lessonId=1050718284&courseId=1004570029
我直接从Octave的基础操作开始，因为前面的内容的课堂ppt都讲的很详细了
原文链接：Octave简要语法记录

• Octave是一个科学计算及数值分析的工具，和Matlab类似，不过Octave是开源并且免费的，占用空间小。而Matlab包含大量面向各种应用领域的工具箱，因此需要付费，并且占用空间大。
  对于一般科学计算、数据分析、绘图而言，Octave的功能已经足够用了，并且Octave最初是模彷Matlab设计，语法基本上与Matlab一致，严谨编写的代码应同时可在Matlab及Octave上运行，但是两者具体而言还是有很多细节上差别。
  对于机器学习而言，至少 Andrew Ng 说他的课程 Octave 是够用了，并且课程算法实现采用 Octave 。在编程语言上，Andrew Ng 称，在硅谷，机器学习工程师一般都先采用 Octave 这样的软件建模，跑数据，之后觉得模型不错再用 C++、Java之类的编程语言实现。因为机器学习算法用 Octave 实现起来比 Python、R、C++、Java之类的计算机编程语言要快捷很多，俗话说磨刀不误砍柴工。因此还是有必要学习一下Octave的基本用法，平时跑个数据什么的。

官网：http://www.gnu.org/software/octave/
下面是Octave的操作界面

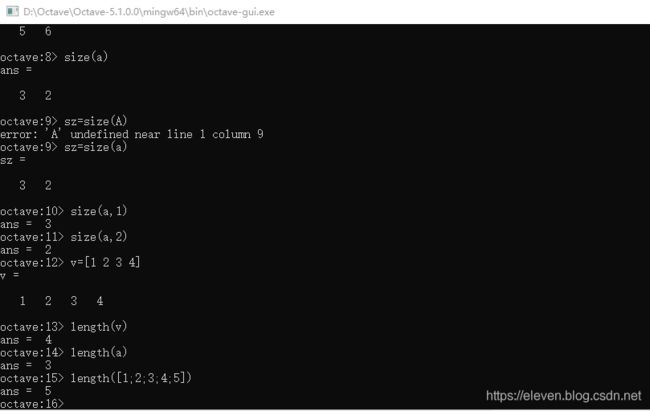
这一部分我们一般只对向量使用length，不会对矩阵使用，因为容易产生歧义，当矩阵是多行多列的时候

基础操作

rouge 对 Octave 的代码高亮有些问题，先凑合着这看吧。。。

以下均在CLI交换下输入

% 代表注释
% 改变 Octave 提示符
PS1(’>> ');
% 改变工作目录
cd ‘c:/path/to/desired/directory name’
% 其中对于 / 不需要额外的转义字符
%% 基础操作和变量赋值
5+6
3-2
5*8
1/2
2^6 % 2的6次方
1 == 2 % 逻辑判断
1 ~= 2 % 不等于不是 “!=”
1 && 0 % 与
1 || 0 % 或
xor(1,0) % 异或
%% 变量赋值
a = 3; % 交互式环境下 ；可以抑制变量的输出
b = ‘hi’;
c = 3>=1;

% 变量显示:
a = pi
disp(a)
disp(sprintf(‘2 decimals: %0.2f’, a))
disp(sprintf(‘6 decimals: %0.6f’, a))
format long
a
format short
a
%% 向量和矩阵
A = [1 2; 3 4; 5 6]

v = [1 2 3]
v = [1; 2; 3]
v = [1:0.1:2] % 从1到2（包含）步长为0.1 绘制坐标轴时非常有用
v = 1:6 % 从1到6,步长为1

C = 2ones(2,3) % 同 C = [2 2 2; 2 2 2]
w = ones(1,3) % 1x3 全1向量
w = zeros(1,3) % 1x3 全0向量
w = rand(1,3) % 矩阵的所有值服从[0,1]均匀分布(uniform distribution)
w = randn(1,3) % 矩阵的所有值服从均值为0，方差为1的正态分布(normal distribution)，注意加分号
w = -6 + sqrt(10)(randn(1,10000)); % (均值 = -6, 方差 = 10)
hist(w) % 绘制10个方块的直方图(histogram) (默认)
hist(w,50) % 绘制50个方块的直方图
% 注意: 如果 hist() 一直未响应, 尝试使用 “graphics_toolkit(‘gnu_plot’)”

I = eye(4) % 4x4 单位矩阵(identity matrix)

% help 帮助
help eye
help rand
help help

数据处理

%% 维数显示
sz = size(A) % 结果为1x2 矩阵: [(行数) (列数)]
size(A,1) % A的行数
size(A,2) % A的列数
length(v) % 行、列最长的那个维数
%% 读写数据
pwd % 显示当前环境位置
cd ‘C:\Users\jinpf\Octave files’ % 更改目录
ls % 显示当前目录下的文件名
load q1y.dat % 或者, load(‘q1y.dat’),其中q1y.dat和q1x.dat的内容如下文所示
load q1x.dat
who % 显示工作环境中已设置的所有变量
whos % 显示工作环境中已设置的所有变量 (包括具体信息)
clear q1y % clear 命令如果没带参数则清空所有变量
v = q1x(1:10); % q1x的前10个元素 (按列计算)
save hello.mat v; % 将v存入文件 hello.mat
save hello.txt v -ascii; % 以ascii存储
% fopen, fread, fprintf, fscanf 同样可以用于读写数据
%% 索引
A(3,2) % 索引采用 (行,列)
A(2,:) % 第二行
% ":"代表该维所有元素
A(:,2) % 第二列
A([1 3]? % 显示第一、三行

A(:,2) = [10; 11; 12] % 对第二列赋值
A = [A, [100; 101; 102]]; % 添加列元素
A(? % 将所有元素转行为列向量
% 数据组合
A = [1 2; 3 4; 5 6]
B = [11 12; 13 14; 15 16] % 和A维度一样
C = [A B]
C = [A, B]
C = [A; B]
附 q1y.dat:

3999
3299
3690
2320
5399
2999
3149
1989
2120
2425
2399
3470
3299
6999
2599
4499
1509
1667
5948
4718
3932
2011
4538
2251
2617
4084
3523
附 q1x.dat

2104 3
1600 3
2400 3
1416 2
3000 4
1985 4
1534 3
1427 3
1380 3
1494 3
1940 4
2000 3
1890 3
4478 5
1268 3
1437 3
1239 3
2132 4
4215 4
2162 4
1664 2
2238 3
2567 4
1200 3
852 2
1852 4
1203 3

矩阵运算

%% 初始化变量
A = [1 2;3 4;5 6]
B = [11 12;13 14;15 16]
C = [1 1;2 2]
v = [1;2;3]
%% 矩阵运算
A * C % 矩阵乘
A .* B % 元素单位乘
% A .* C 或 A * B 出错
A .^ 2 % 元素单位平方
1./v % 元素单位倒数
log(v) % 元素单位
exp(v)
abs(v)
-v

v + ones(length(v), 1) % 同 v + 1

A’ % 矩阵转置
%% 常用函数

% max (or min)
a = [1 15 2 0.5]
val = max(a)
[val,ind] = max(a) % val 赋值为向量中最大的元素 ind 赋值为该最大元素的索引
val = max(A) % 如果A是矩阵，返回每列最大元素

% compare values in a matrix & find
a < 3 % 返回元素是否小于3的判断
find(a < 3) % 返回小于3的位置
A = magic(3) % 产生一个3*3魔方阵 - 矩阵所有行列对角线之和相同 - 机器学习不常用
[r,c] = find(A>=7) % 返回符合条件的元素的行列，r、c分别以列向量存储

% sum, prod
sum(a) % 求和
prod(a) % 求乘积
floor(a) % or ceil(a) % 去下整、去上整
max(rand(3),rand(3)) % 返回逐元素对比，较大的矩阵
max(A,[],1) % 返回每列最大元素 等同于max(A)
max(A,[],2) % 返回每行最大元素
max(max(A)) % 矩阵A最大元素
A = magic(9)
sum(A,1)
sum(A,2)
sum(sum( A .* eye(9) )) % 对角线元素求和
sum(sum( A .* flipud(eye(9)) )) % 斜对角线元素和 flipud 上下翻转
% 矩阵求逆 （伪逆）
pinv(A) % inv(A’*A)*A’

绘图

%% plotting 绘图
t = [0:0.01:0.98];
y1 = sin(2pi4t);
plot(t,y1);
y2 = cos(2pi4t);
hold on; % 在上一个图中继续画 “hold off” 来关闭
plot(t,y1,‘r’);
xlabel(‘time’);
ylabel(‘value’);
legend(‘sin’,‘cos’);
title(‘my plot’);
print -dpng ‘myPlot.png’
close; % 或"close all"关闭所有
figure(1); plot(t, y1);
figure(2); plot(t, y2);
figure(1), clf; % 指定某个图 clf - 清空图
subplot(1,2,1); % 分成 1x2 的图, 访问第一个图
plot(t,y1);
subplot(1,2,2); % 分成 1x2 的图, 访问第二个图
plot(t,y2);
axis([0.5 1 -1 1]); % 改变坐标范围
%% 绘制矩阵
figure;
imagesc(magic(15)), colorbar, colormap gray;
% comma-chaining function calls.
a=1,b=2,c=3 % 逗号分割，连续几条命令，输出结果
a=1;b=2;c=3; % 分号分割，连续几条命令，不输出结果

控制语句 for while if

v = zeros(10,1);
for i=1:10,
v(i) = 2^i; % 缩进仅为美观 不影响程序
end;

% Can use “break” “continue” inside for while loops to control execution.

i = 1;
while i <= 5,
v(i) = 100;
i = i+1;
end

i = 1;
while true,
v(i) = 999;
i = i+1;
if i == 6,
break;
end;%这里的end是对应if
end;%这里是对应while；

if v(1)==1,
disp(‘The value is one!’);
elseif v(1)==2,
disp(‘The value is two!’);
else
disp(‘The value is not one or two!’);
end

函数定义

每个函数定义在一个文件中，文件名为 “functionName.m”，其中文件名和定义函数名需要保持一致，以便调用。

如定义 “squareThisNumber.m”：

function y = squareThisNumber(x)
y = x^2;
在Octave中调用需要将函数定义放到Octave运行Path中。

方案一：
cd /path/to/function
方案二：
addpath(’/path/to/function/’)
savepath % 方便以后使用
之后调用函数：

functionName(args)
Octave函数可以返回多个值：

%% 定义
function [y1, y2] = squareandCubeThisNo(x)
y1 = x^2
y2 = x^3
%% 调用
[a,b] = squareandCubeThisNo(x)