Systems biology informed deep learning for inferring parameters and hidden dynamics
- 作者:Alireza Yazdani1, Lu Lu1, Maziar Raissi2, George Em Karniadakis1
- 单位:
- Division of Applied Mathematics, Brown University, Providence, RI 02912, USA,
- Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
1 动机:
- 在系统集生物反应的数学模型可由带未知参数的ODE描述,使用reliable and robust的算法进行参数推断以及解的预测是系统生物学中的关键核心
2 主要研究内容:
- 提出a new systems-biology-informed deep learning algorithm,该算法能够融合ODE到神经网络中
- 使用少量分散和噪声测量,能够对未观察的species、外部的动力学以及未知模型参数的dynamics进行推断
- 在三种不同的benchmark问题上进行测试
3 问题与方法
3.1 问题定义
KaTeX parse error: {equation} can be used only in display mode. (1)
其中, x = ( x 1 , x 2 , … , x S ) \mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{S}\right) x=(x1,x2,…,xS)是 S S S, p = ( p 1 , p 2 , … , p K ) \mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{K}\right) p=(p1,p2,…,pK)是模型的 K K K个参数,需要被估计。一旦 p p p确定,该系统的ODE就能确定。 y \mathbf{y} y是 M M M个测量信号(带有高斯噪音的数据)。 h \mathbf{h} h由实验设计确定,可以为any function,在这假设为线性函数
( y 1 y 2 ⋯ y M ) = ( x s 1 x s 2 ⋯ x s M ) + ( ϵ s 1 ϵ s 2 ⋯ ϵ s M ) \left(\begin{array}{c} y_{1} \\ y_{2} \\ \cdots \\ y_{M} \end{array}\right)=\left(\begin{array}{c} x_{s_{1}} \\ x_{s_{2}} \\ \cdots \\ x_{s_{M}} \end{array}\right)+\left(\begin{array}{c} \epsilon_{s_{1}} \\ \epsilon_{s_{2}} \\ \cdots \\ \epsilon_{s_{M}} \end{array}\right) ⎝ ⎛y1y2⋯yM⎠ ⎞=⎝ ⎛xs1xs2⋯xsM⎠ ⎞+⎝ ⎛ϵs1ϵs2⋯ϵsM⎠ ⎞(2)
3.2 Systems-informed neural networks and parameter inference

KaTeX parse error: {equation} can be used only in display mode.(3)
L d a t a ( θ ) = ∑ m = 1 M w m d a t a L m d a t a = ∑ m = 1 M w m d a t a [ 1 N d a t a ∑ n = 1 N d a t a ( y m ( t n ) − x ^ s m ( t n ; θ ) ) 2 ] \mathcal{L}^{d a t a}(\boldsymbol{\theta})=\sum_{m=1}^{M} w_{m}^{d a t a} \mathcal{L}_{m}^{d a t a}=\sum_{m=1}^{M} w_{m}^{d a t a}\left[\frac{1}{N^{d a t a}} \sum_{n=1}^{N^{d a t a}}\left(y_{m}\left(t_{n}\right)-\hat{x}_{s_{m}}\left(t_{n} ; \boldsymbol{\theta}\right)\right)^{2}\right] Ldata(θ)=∑m=1MwmdataLmdata=∑m=1Mwmdata[Ndata1∑n=1Ndata(ym(tn)−x^sm(tn;θ))2](4)
L o d e ( θ , p ) = ∑ s = 1 S w s o d e L s o d e = ∑ s = 1 S w s o d e [ 1 N o d e ∑ n = 1 N o d e ( d x ^ s d t ∣ τ n − f s ( x ^ s ( τ n ; θ ) , τ n ; p ) ) 2 ] \mathcal{L}^{o d e}(\boldsymbol{\theta}, \mathbf{p})=\sum_{s=1}^{S} w_{s}^{o d e} \mathcal{L}_{s}^{o d e}=\sum_{s=1}^{S} w_{s}^{o d e}\left[\frac{1}{N^{o d e}} \sum_{n=1}^{N^{o d e}}\left(\left.\frac{d \hat{x}_{s}}{d t}\right|_{\tau_{n}}-f_{s}\left(\hat{x}_{s}\left(\tau_{n} ; \boldsymbol{\theta}\right), \tau_{n} ; \mathbf{p}\right)\right)^{2}\right] Lode(θ,p)=∑s=1SwsodeLsode=∑s=1Swsode[Node1∑n=1Node(dtdx^s∣ ∣τn−fs(x^s(τn;θ),τn;p))2](5)
L a u x ( θ ) = ∑ s = 1 S w s a u x L s a u x = ∑ s = 1 S w s a u x ( x s ( T 0 ) − x ^ s ( T 0 ; θ ) ) 2 + ( x s ( T 1 ) − x ^ s ( T 1 ; θ ) ) 2 2 \mathcal{L}^{a u x}(\boldsymbol{\theta})=\sum_{s=1}^{S} w_{s}^{a u x} \mathcal{L}_{s}^{a u x}=\sum_{s=1}^{S} w_{s}^{a u x} \frac{\left(x_{s}\left(T_{0}\right)-\hat{x}_{s}\left(T_{0} ; \boldsymbol{\theta}\right)\right)^{2}+\left(x_{s}\left(T_{1}\right)-\hat{x}_{s}\left(T_{1} ; \boldsymbol{\theta}\right)\right)^{2}}{2} Laux(θ)=∑s=1SwsauxLsaux=∑s=1Swsaux2(xs(T0)−x^s(T0;θ))2+(xs(T1)−x^s(T1;θ))2(6)
前两项为data loss、ODE loss,最后一项为auxiliary loss,是系统的额外信息,包含两个时间点 T 0 T_{0} T0和 T 1 T_{1} T1,第一项与第三项属于监督loss,第二项为无监督loss。
- 在(4-6)中系数 M + 2 S M+2S M+2S个损失项,在这篇论文中,手动选择权重系数,使得加权的损失在网络训练中保持相同的数量级(待理解,为什么要一样数据集,是有什么特性吗)
- 对于第一项 t 1 , t 2 , … , t N d a t a t_{1}, t_{2}, \ldots, t_{N^{d a t a}} t1,t2,…,tNdata,随机采时间点;对于ODE loss中的time instant τ 1 , τ 2 , … , τ N o d e \tau_{1}, \tau_{2}, \ldots, \tau_{N^{o d} e} τ1,τ2,…,τNode在一个等距离的网格中选择;第****三项 T 0 T_{0} T0为初值点, T 1 T_{1} T1可以在训练时间链上选择任意时间(但是不要离 T 0 T_{0} T0太近)
4 Analysis of system’s identifiability
- 在systems identification problems中,主要有两类identifiability,structural和practical。结构不可识别性由于 y y y解的冗余参数化,这是由于观测数据 y y y到 x x x的insufficient的映射 h \mathbf{h} h由于实验数据被忽视,出现了practical非识别性
- 结构上的可识别参数也可能是practical非识别性。practical非识别性与测量数据数量与质量有关,在一个无限的置信区间显示。
步骤
- 先考虑监督的loss(第一项和第三项)进行训练,使得网络能够快速拟合观察数据
- 然后再用三种损失进行训练
通过实验发现,这种两阶段训练策略加快了网络的收敛速度。
5 实验
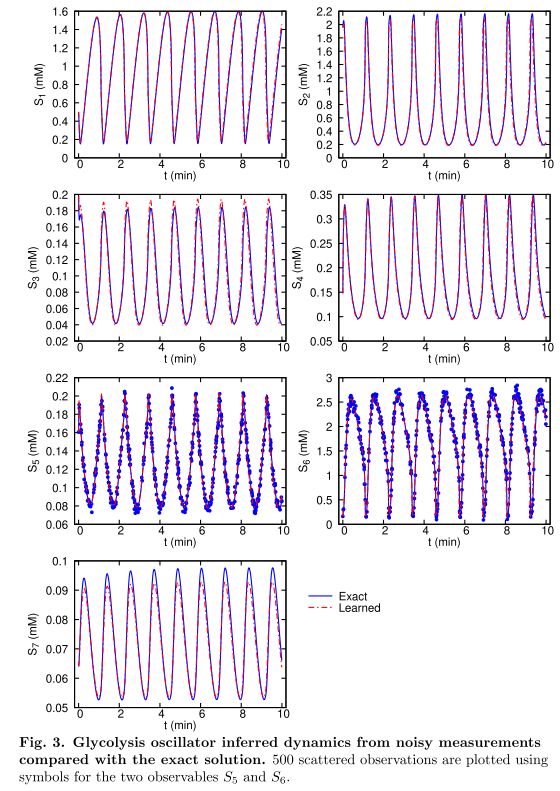
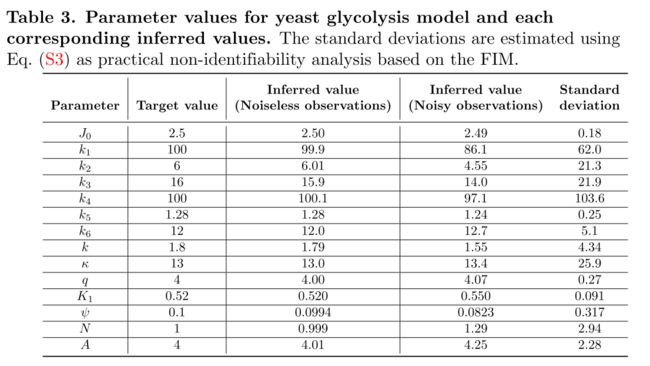
5.1 yeast glycolysis
- 添加的ODE loss能防止网络过拟合
- Standard deviation是基于FIM得到,结构/实际可识别性分析或bootstrapping方法获得参数置信区间,这里使用的是FIM
6 总结
- 利用网络训练拟合模型参数
- 提出了system-biology -informed 神经算法,能够可靠而准确的推断hidden dynamics
- 能够用很少的观测数据对dynamics和模型参数进行推断