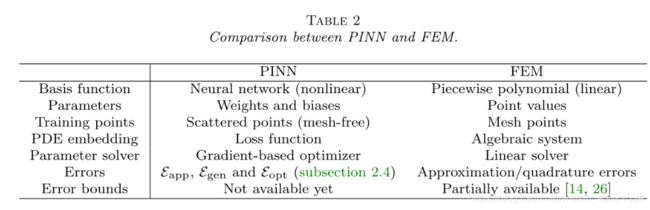
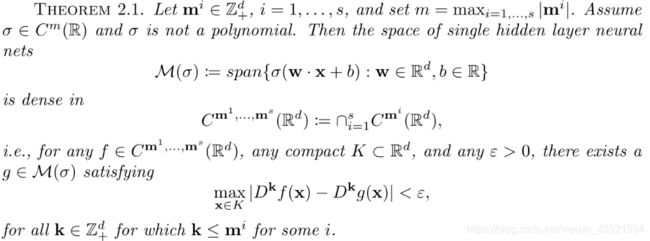DEEPXDE

论文信息

题目：DEEPXDE: A DEEP LEARNING LIBRARY FOR SOL VING DIFFERENTIAL EQUATIONS

作者：LU LU, XUHUI MENG, ZHIPING MAO, AND GEORGE EM KARNIADAKIS

期刊会议： Computational Physics，Machine Learning

年份：19

论文地址：代码：

基础补充

内容

动机

动机：

• 近年来在深度学习在计算机视觉，自然语言等方面得到了广泛应用，尽管在这些和相关领域取得了显著的成功，但深度学习还没有广泛应用于科学计算领域；
• 然而，最近，通过深度学习求解偏微分方程(PDEs)，如标准微分形式或积分形式，已经成为科学机器学习下一个潜在的新的子领域；
• 特别的，用一种近似于PDE解的神经网络来代替传统的数值离散方法

问题定义：求解微分方程
$$f\left(\mathbf{x};\frac{\partial u}{\partial x_1},\dots ,\frac{\partial u}{\partial x_d};\frac{{\partial }^{2}u}{\partial x_1\partial x_1},\dots ,\frac{{\partial }^{2}u}{\partial x_1\partial x_d};\dots ;\lambda \right)=0,\mathbf{x}\in \Omega$$

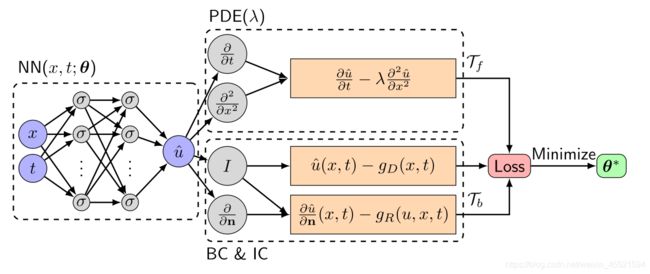
PINN

PPINN求解：$$\mathcal{L}(\mathbf{\theta };\mathcal{T})=w_f{\mathcal{L}}_f\left(\mathbf{\theta };{\mathcal{T}}_f\right)+w_b{\mathcal{L}}_b\left(\mathbf{\theta };{\mathcal{T}}_b\right)$$其中：$$\begin{array}{rl}{\mathcal{L}}_f\left(\mathbf{\theta };{\mathcal{T}}_f\right)& =\frac{1}{\left|{\mathcal{T}}_f\right|}\sum _{\mathbf{x}\in {\mathcal{T}}_f}{\Vert f\left(\mathbf{x};\frac{\partial \hat{u}}{\partial x_1},\dots ,\frac{\partial \hat{u}}{\partial x_d};\frac{{\partial }^2\hat{u}}{\partial x_1\partial x_1},\dots ,\frac{{\partial }^2\hat{u}}{\partial x_1\partial x_d};\dots ;\mathbf{\lambda }\right)\Vert }_2^2\\ {\mathcal{L}}_b\left(\mathbf{\theta };{\mathcal{T}}_b\right)& =\frac{1}{\left|{\mathcal{T}}_b\right|}\sum _{\mathbf{x}\in {\mathcal{T}}_b}\Vert \mathcal{B}(\hat{u},\mathbf{x}){\Vert }_2^2\end{array}$$

其中$\mathcal{L}$为residual points，选择的策略可以为- 我们可以在训练开始时指定residual points，可以是格点上的网格点，也可以是随机点，训练过程中不改变它们；

• 在每次优化迭代中，我们可以随机选择不同的residual points；
• 我们可以在训练过程中自适应地改善residual points的位置(Residual-based adaptive refinement (RAR))。
  

特别注意：

• 因为L-BFGS使用损失函数的二阶导数，而Adam只依赖于一阶导数，所以L-BFGS可以找到比Adam迭代次数少的较好的解，但是对于 stiff solutions，L-BFGS更有可能被卡在一个糟糕的局部最小值上；
• 当residual points数目很大时，每一次迭代计算损失函数和梯度花费很大，可以考虑不使用所有residual points，把这些residual points分成一小批一小批，每次迭代只用一批，这种方法称为小批量梯度下降

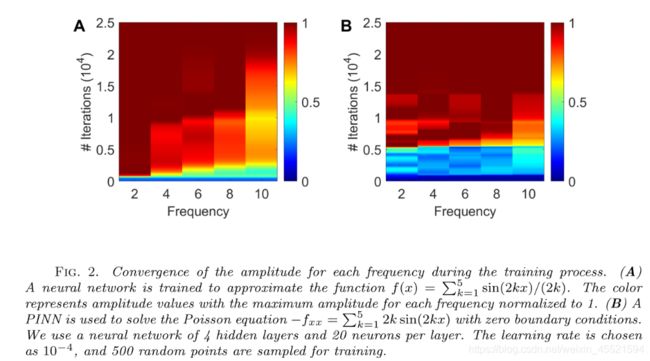
PINN与NN对比目标：$$f(x)=\sum _{k=1}^5\sin (2kx)/(2k)\text{ in }[-\pi ,\pi ]$$函数逼近:神经网络(NN)是低地频到高频学习目标函数的，但是PINNs的学习方式是所有频同时学习证明：使用PINN求解PDE比使用NN逼近函数要快

PINN与FEM比较

PINN逼近理论

说明：定理主要表明，具有足够神经元的前馈神经网络可以同时一致地逼近任意函数及其偏导数，就是存在可以求解PDE的神经网络

PINN误差分析
$$\mathcal{E}:=\Vert {\tilde{u}}_{\mathcal{T}}-u\Vert \le \underset{{\mathcal{E}}_{\mathrm{o}\mathrm{p}\mathrm{t}}}{\Vert {\tilde{u}}_{\mathcal{T}}-u_{\mathcal{T}}\Vert }+\underset{{\mathcal{E}}_{\mathrm{g}\mathrm{e}\mathrm{n}}}{\Vert u_{\mathcal{T}}-u_{\mathcal{F}}\Vert }+\underset{{\mathcal{E}}_{\mathrm{a}\mathrm{p}\mathrm{p}}}{\Vert u_{\mathcal{F}}-u\Vert }$$
其中：$\mathcal{F}$表示可以由我们选择的神经网络结构表示的所有函数的族
$u$是PDE的解
$u_{\mathcal{F}}$是$\mathcal{F}$中最接近 $u$的函数
$u_{\mathcal{T}}$，因为训练是在$\mathcal{T}$上
${\tilde{u}}_{\mathcal{T}}$，优化器中求出的逼近解
$u_{\mathcal{F}}-u$是逼近误差
$u_{\mathcal{T}}-u_{\mathcal{F}}$是泛化误差
${\tilde{u}}_{\mathcal{T}}-u_{\mathcal{T}}$是优化误差

PINN求解积分微分方程利用经典方法估计积分例如 Gaussian quadrature等方法，就在PINN中加入了一个新的discretization error ${\mathcal{E}}_{dis}$例如使用Gaussian quadratur方法：$$\frac{dy}{dx}+y(x)={\int }_0^x{e}^{t-x}y(t)dt$$变换$${\int }_0^x{e}^{t-x}y(t)dt\approx \sum _{i=1}^n{w}_i{e}^{t_i(x)-x}y\left(t_i(x)\right)$$得到:$$\frac{dy}{dx}+y(x)\approx \sum _{i=1}^n{w}_i{e}^{t_i(x)-x}y\left(t_i(x)\right)$$

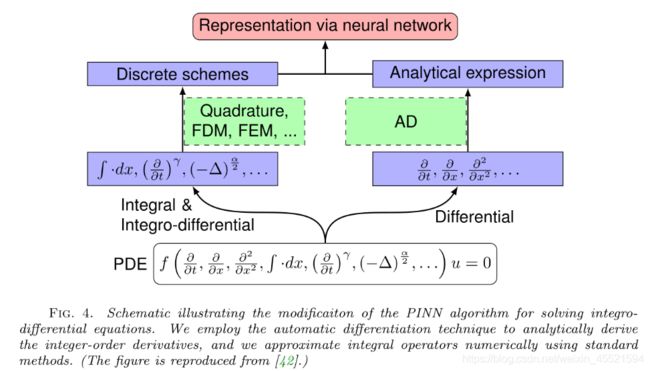
PINNs求解逆问题相比于forward增加了$$\mathcal{L}(\mathbf{\theta },\mathbf{\lambda };\mathcal{T})=w_f{\mathcal{L}}_f\left(\mathbf{\theta },\mathbf{\lambda };{\mathcal{T}}_f\right)+w_b{\mathcal{L}}_b\left(\mathbf{\theta },\mathbf{\lambda };{\mathcal{T}}_b\right)+w_i{\mathcal{L}}_i\left(\mathbf{\theta },\mathbf{\lambda };{\mathcal{T}}_i\right)$$其中:$${\mathcal{L}}_i\left(\mathbf{\theta },\mathbf{\lambda };{\mathcal{T}}_i\right)=\frac{1}{\left|{\mathcal{T}}_i\right|}\sum _{\mathbf{x}\in {\mathcal{T}}_i}\Vert \mathcal{I}(\hat{u},\mathbf{x}){\Vert }_2^2$$

RAR(Residual-based adaptive refinement 基于残差的自适应细化)
问题：residual points通常是在域里面随机选择的，在大多数情况下都能表现得很好，但是，对于某些具有陡峭（steep）梯度的解的偏微分方程，它可能不是有效的，为了设计好residual point的分布，提出了RAR。

使用：

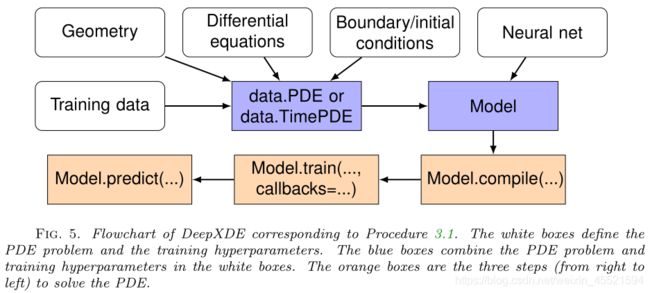
创新：提出RAR方法能够加速训练效率

实验

实验1：
$$\begin{array}{rl}-\Delta u(x,y)& =1,(x,y)\in \Omega \\ u(x,y)& =0,(x,y)\in \partial \Omega \end{array}$$

实验2：
$$\begin{array}{ll}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\nu \frac{{\partial }^{2}u}{\partial x^2},& x\in [-1,1],t\in [0,1]\\ u(x,0)=-\sin (\pi x),& u(-1,t)=u(1,t)=0\end{array}$$
采用PINN和PINN（RAR）方法训练数据2540 个样本

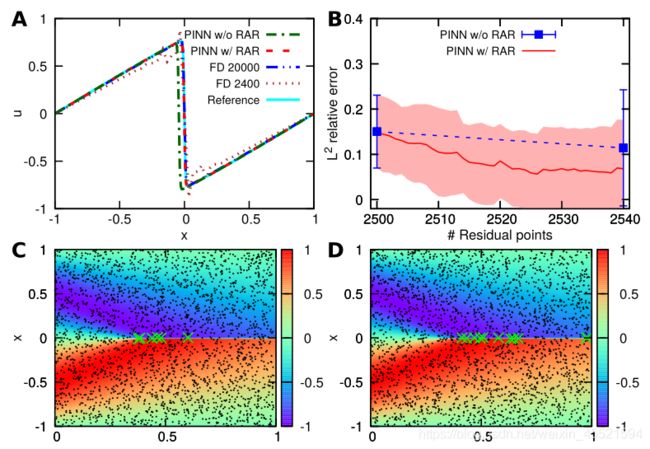
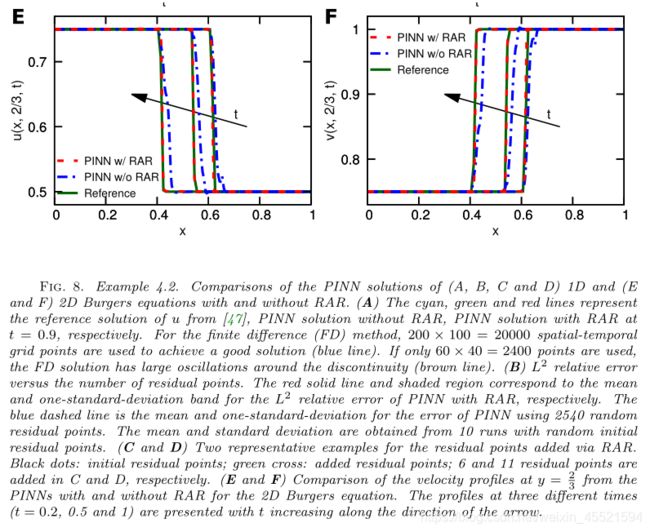
结论：- A和B看出相比于有限差分方法同样的数据点结果更好- 在C和D中可以看到，新加的点都在 sharp 接口

实验3:逆问题：
$$\frac{dx}{dt}=\rho (y-x),\frac{dy}{dt}=x(\sigma -z)-y,\frac{dz}{dt}=xy-\beta z$$

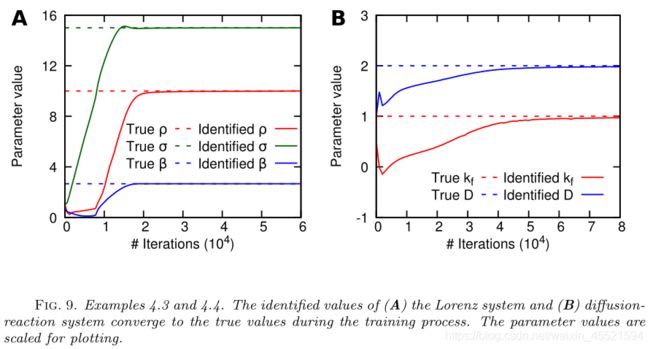
结论

介绍求解不同类型偏微分方程的物理神经网络(PINNs)的算法、近似理论和误差分析。与传统的数值方法相比，PINN采用了自动微分来处理微分算子而且是无网格的，提出一种基于残差的自适应细化(RAR)方法来改善训练过程中残差点的分布，从而提高训练效率

不懂

• 定理2.1实际证明过程不太清楚

可借鉴地方

• 提出RAR的方法提供训练效率，对于一些steep梯度的微分方程很适用