经典卷积神经网络——LeNet-5

由于该CNN结构过于经典，网上相关的文章和参考文献对其介绍很多，在这就不详细说了。本文主要讲解其结构的原理和使用Pytorch如何实现。原论文链接：http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf

原理：

LeNet-5[LeCun et al., 1998] 虽然提出的时间比较早，但是是一个非常成功的神经网络模型。基于LeNet-5的手写数字识别系统在90年代被美国很多银行使用，用来识别支票上面的手写数字体。LeNet-5的网络结构图如图：

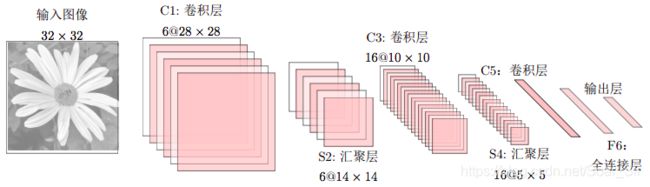
该图片根据LeNet-5绘制

不计输入层，LeNet-5共有7层，每一层的结构为：

1. 输入层：输入图像大小为32 × 32 = 1024。
2. C1层是卷积层，使用6个5 × 5的滤波器，得到6组大小为28 × 28 = 784的特征映射。因此，C1层的神经元数量为6 × 784 = 4, 704，可训练参数数量为6 × 25 + 6 = 156，连接数为156 × 784 = 122, 304（包括偏置在内，下同）。
3. S2层为汇聚层(池化层)，采样窗口为2 × 2，使用平均汇聚，并使用一个如下公式的非线性函数。神经元个数为 6 × 14 × 14 = 1, 176，可训练参数数量为6 × (1 + 1) = 12，连接数为6 × 196 × (4 + 1) = 5, 880。
4. C3层为卷积层。LeNet-5中用一个连接表来定义输入和输出特征映射之间的依赖关系，如图所示，共使用60个5 × 5的滤波器，得到16组大小为 10 × 10的特征映射。神经元数量为16 × 100 = 1, 600，如果不使用连接表，可训练参数数量需要(60 × 25) + 16 = 1, 516，连接数为100 × 1, 516 = 151, 600。
   
5. S4层是一个汇聚层（池化层），采样窗口为2 × 2，得到16个5 × 5大小的特征映射，可训练参数数量为16 × 2 = 32，连接数为16 × 25 × (4 + 1) = 2000。
6. C5 层是一个卷积层，使用 120 × 16 = 1, 920 个 5 × 5 的滤波器，得到 120组大小为1 × 1的特征映射。C5层的神经元数量为120，可训练参数数量为1, 920 × 25 + 120 = 48, 120，连接数为120 × (16 × 25 + 1) = 48, 120。
7. F6层是一个全连接层，有84个神经元，可训练参数数量为84 × (120 + 1) =10, 164。连接数和可训练参数个数相同，为10, 164。
8. 输出层：输出层由10个欧氏径向基函数（Radial Basis Function，RBF）函数组成。

PyTorch代码实现：

由于本人水平有限，目前自己手动还写不出来CNN的代码，我就把Pytorch官方的tutioral和code搬运过来了。

Neural networks can be constructed using the torch.nn package.

Now that you had a glimpse of autograd, nn depends on autograd to define models and differentiate them. An nn.Module contains layers, and a method forward(input)that returns the output.

For example, look at this network that classifies digit images:

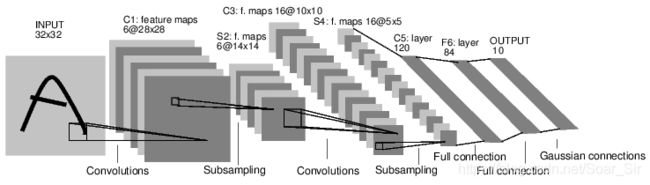
图片来源于Paper[LeCun et al., 1998]

ConvNet

It is a simple feed-forward network. It takes the input, feeds it through several layers one after the other, and then finally gives the output.

A typical training procedure for a neural network is as follows:

• Define the neural network that has some learnable parameters (or weights)
• Iterate over a dataset of inputs
• Process input through the network
• Compute the loss (how far is the output from being correct)
• Propagate gradients back into the network’s parameters
• Update the weights of the network, typically using a simple update rule:
  • weight = weight - learning_rate * gradient

Let’s define this network:

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

Out：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

You just have to define the forward function, and the backward function (where gradients are computed) is automatically defined for you using autograd. You can use any of the Tensor operations in the forward function.

The learnable parameters of a model are returned by net.parameters()

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

Out：

10
torch.Size([6, 1, 3, 3])

Let try a random 32x32 input. Note: expected input size of this net (LeNet) is 32x32. To use this net on MNIST dataset, please resize the images from the dataset to 32x32.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

Out：

tensor([[ 0.0242, -0.0651,  0.1240, -0.0556, -0.0722,  0.1715,  0.0445, -0.0076,
         -0.0727,  0.1194]], grad_fn=)

Zero the gradient buffers of all parameters and backprops with random gradients:

net.zero_grad()
out.backward(torch.randn(1, 10))

Note
torch.nn only supports mini-batches. The entire torch.nn package only supports inputs that are a mini-batch of samples, and not a single sample.For example, nn.Conv2d will take in a 4D Tensor of nSamples x nChannels x Height x Width.If you have a single sample, just use input.unsqueeze(0) to add a fake batch dimension.

Before proceeding further, let’s recap all the classes you’ve seen so far.
Recap:

• torch.Tensor - A multi-dimensional array with support for autograd operations like backward(). Also holds the gradient w.r.t. the tensor.
• nn.Module - Neural network module. Convenient way of encapsulating parameters, with helpers for moving them to GPU, exporting, loading, etc.
• nn.Parameter - A kind of Tensor, that is automatically registered as a parameter when assigned as an attribute to a Module.
• autograd.Function - Implements forward and backward definitions of an autograd operation. Every Tensor operation creates at least a single Function node that connects to functions that created a Tensor and encodes its history.

At this point, we covered:

• Defining a neural network
• Processing inputs and calling backward

Still Left:

• Computing the loss
• Updating the weights of the network

Loss Function

A loss function takes the (output, target) pair of inputs, and computes a value that estimates how far away the output is from the target.

There are several different loss functions under the nn package . A simple loss is: nn.MSELoss which computes the mean-squared error between the input and the target.

For example:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Out：

tensor(1.7215, grad_fn=)

Now, if you follow loss in the backward direction, using its .grad_fn attribute, you will see a graph of computations that looks like this:

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

So, when we call loss.backward(), the whole graph is differentiated w.r.t. the loss, and all Tensors in the graph that has requires_grad=True will have their .grad Tensor accumulated with the gradient.

For illustration, let us follow a few steps backward:

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

Out：

Backprop

To backpropagate the error all we have to do is to loss.backward(). You need to clear the existing gradients though, else gradients will be accumulated to existing gradients.

Now we shall call loss.backward(), and have a look at conv1’s bias gradients before and after the backward.

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

Out：

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0118,  0.0061,  0.0076, -0.0030, -0.0062, -0.0139])

Now, we have seen how to use loss functions.

Update the weights

The simplest update rule used in practice is the Stochastic Gradient Descent (SGD):
weight = weight - learning_rate * gradient

We can implement this using simple python code:

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

However, as you use neural networks, you want to use various different update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc. To enable this, we built a small package: torch.optim that implements all these methods. Using it is very simple:

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

Total running time of the script: ( 0 minutes 3.125 seconds)

References:

[1] https://nndl.github.io/nndl-book.pdf
[2] https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html#sphx-glr-beginner-blitz-neural-networks-tutorial-py