线性判别准则（LDA）与线性分类编程（SVM）实践

一、内容提示

学习线性判别准则（LDA）和线性分类算法（支持向量机,SVM）。采用Sklearn库
1、编程生成模拟数据集，进行LDA算法练习；
2、对月亮数据集进行SVM分类，分别采用线性核、多项式核和高斯核以及不同的参数（比如惩罚系数C），对比分析结果。

二、线性判别准则（LDA）

2.1 LDA简介

线性判别分析（Linear Discriminant Analysis，简称LDA）: 是一种经典的有监督数据降维方法。LDA的主要思想是将一个高维空间中的数据投影到一个较低维的空间中，且投影后要保证各个类别的类内方差小而类间均值差别大，这意味着同一类的高维数据投影到低维空间后相同类别的聚在一起，而不同类别之间相距较远。如下图将二维数据投影到一维直线上：

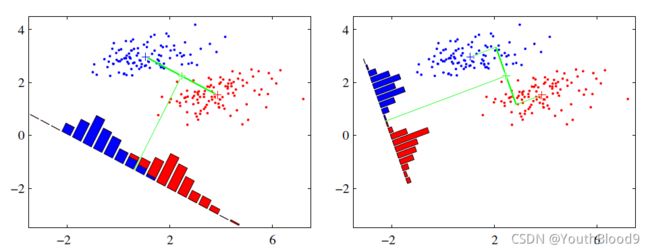
上图提供了两种方式，哪一种投影方式更好呢？从图上可以直观的看出右边的比左边的投影后分类的效果好，因此右边的投影方式是一种更好地降维方式。

2.2 LDA实现代码

此处采用随机数据集训练并进行训练

# 导入要使用的包
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as lda#导入LDA算法
from sklearn.datasets._samples_generator import make_classification #导入分类生成器
import matplotlib.pyplot as plt #导入画图用的工具
import numpy as np
import pandas as pd


# 获得数据集并进行训练，用上面导入的make_classification函数获得数据集，里面的参数含义参考备注
x,y=make_classification(n_samples=500,n_features=2,n_redundant=0,n_classes=2,n_informative=1,n_clusters_per_class=1,class_sep=0.5,random_state=100)
"""
n_features :特征个数= n_informative（） + n_redundant + n_repeated
n_informative：多信息特征的个数
n_redundant：冗余信息，informative特征的随机线性组合
n_repeated ：重复信息，随机提取n_informative和n_redundant 特征
n_classes：分类类别
n_clusters_per_class ：某一个类别是由几个cluster构成的

"""
plt.scatter(x[:,0],x[:,1], marker='o', c=y)
plt.show()
x_train=x[:60, :60]
y_train=y[:60]
x_test=x[40:, :]
y_test=y[40:]

• 输出结果显示
  

将数据集分为训练集和测试集，分类比为6：4，训练完之后利用测试集获得准确率
续写代码：

#分为训练集和测试集，进行模型训练并测试
x_train=x[:300, :300]
y_train=y[:300]
x_test=x[200:, :]
y_test=y[200:]
lda_test=lda()
lda_test.fit(x_train,y_train)
predict_y=lda_test.predict(x_test)#获取预测的结果
count=0
for i in range(len(predict_y)):
    if predict_y[i]==y_test[i]:
        count+=1
print("预测准确个数为"+str(count))
print("准确率为"+str(count/len(predict_y)))

• 输出结果显示：
  

三、SVM

3.1 SVM简介

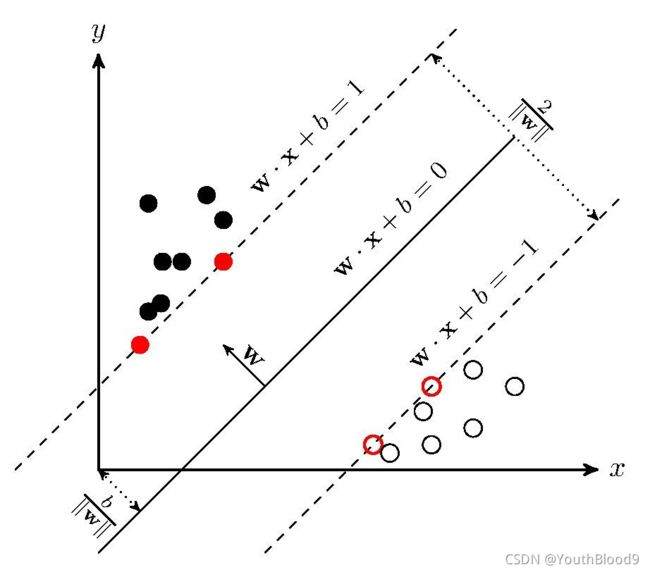
支持向量机（support vector machines, SVM） ：是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

3.2 SVM原理

SVM算法原理建议去看：支持向量机（SVM）——原理篇

四、SVM数据集进行可视化分类

4.1 月亮数据集

4.1.1 线性SVM

代码实现：

# 导入月亮数据集和svm方法
#这是线性svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt #导入画图用的工具


# 获得数据集
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子，nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别，并且只取前两个特征
plt.show()

输出显示：

续写代码：

#进行标准化并训练数据
scaler=StandardScaler()# 标准化
scaler.fit(data_x)#计算训练数据的均值和方差
data_x=scaler.transform(data_x) #再用scaler中的均值和方差来转换X，使X标准化
liner_svc=LinearSVC(C=1e9,max_iter=100000)#线性svm分类器,iter是迭达次数，c值决定的是容错，c越大，容错越小
liner_svc.fit(data_x,data_y)


# 边界绘制函数，为下面可视化分类做准备
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    # meshgrid函数是从坐标向量中返回坐标矩阵
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)#获取预测值
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)


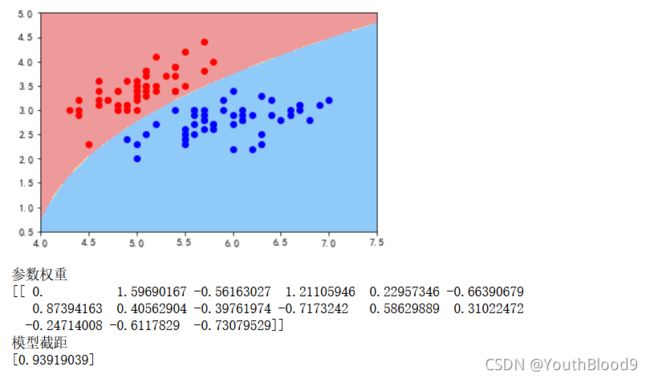
#画图并输出参数权重和模型截距
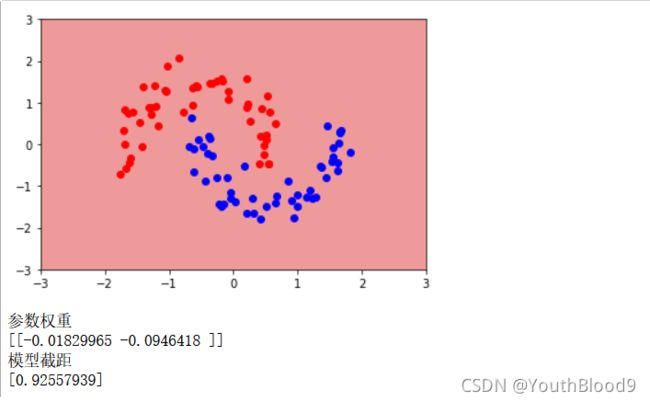
plot_decision_boundary(liner_svc,axis=[-3,3,-3,3])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(liner_svc.coef_)
print('模型截距')
print(liner_svc.intercept_)

• 输出结果显示：
  

这时，图有一点小小的问题（应该只有笔主的输出有问题）。我们换一种试试。

4.1.2 多项式核

代码：

# 导入月亮数据集和svm方法
#这是多项式核svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from sklearn.pipeline import Pipeline #导入python里的管道
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化


#生成数据，也是月亮数据集，和线性svm一致
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子，nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别，并且只取前两个特征
plt.show()#此时同上一部分有输出，此处笔主不再示出

def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    # meshgrid函数是从坐标向量中返回坐标矩阵
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)#获取预测值
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)


#利用pipeline进行一体化编程，为了方便，将它放入函数中
def PolynomialSVC(degree,c=10):#多项式svm
    return Pipeline([
        # 将源数据 映射到 3阶多项式
        ("poly_features", PolynomialFeatures(degree=degree)),
        # 标准化
        ("scaler", StandardScaler()),
        # SVC线性分类器
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42,max_iter=10000))
        ])


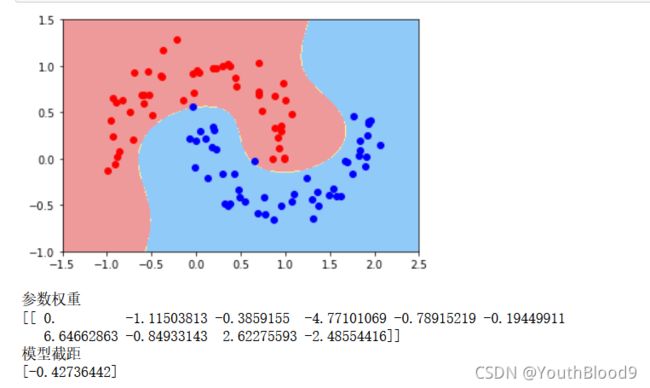
# 进行模型训练并画图
poly_svc=PolynomialSVC(degree=3)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(poly_svc.named_steps['svm_clf'].coef_)
print('模型截距')
print(poly_svc.named_steps['svm_clf'].intercept_)

• 输出结果显示：
  

4.1.3 高斯核

代码：

## 导入包 高斯核
from sklearn import datasets #导入数据集
from sklearn.svm import SVC #导入svm
from sklearn.pipeline import Pipeline #导入python里的管道
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化


#导入数据集
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子，nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别，并且只取前两个特征
plt.show()#此时同样有输出，不再示出

# 边界绘制函数，为下面可视化分类做准备
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    # meshgrid函数是从坐标向量中返回坐标矩阵
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)#获取预测值
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)


#利用pipeline进行一体化编程，为了方便，将它放入函数中
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])


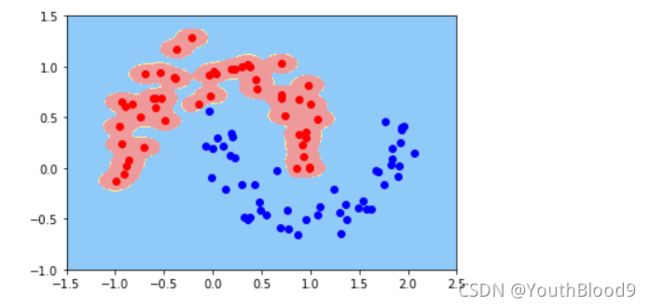
#进行模型训练画出图形，这里面的gamma参数也很重要，gamma参数越大，支持向量越小，和C是差不多，改变gamma的值，判断区域会发生变化
svc=RBFKernelSVC(gamma=100)#gamma参数很重要，gamma参数越大，支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

• 输出结果显示：
  

4.2 鸢尾花数据集

4.2.1 多项式核

代码：
（建议新建一个python3项目）

#这是多项式核svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from sklearn.pipeline import Pipeline #导入python里的管道
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化

#读取鸢尾花数据集
data=datasets.load_iris()
data_x=data.data
data_y=data.target
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别，并且只取前两个特征
data_y=data_y[data_y<2]
plt.show()

• 输出显示：
  
  续写代码：

#绘制边界函数
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    # meshgrid函数是从坐标向量中返回坐标矩阵
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)#获取预测值
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)


#利用pipeline进行一体化编程，为了方便，将它放入函数中
def PolynomialSVC(degree,c=10):#多项式svm
    return Pipeline([
        # 将源数据 映射到 3阶多项式
        ("poly_features", PolynomialFeatures(degree=degree)),
        # 标准化
        ("scaler", StandardScaler()),
        # SVC线性分类器
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42,max_iter=10000))
        ])


# 进行模型训练并画图
poly_svc=PolynomialSVC(degree=4)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[4.0,7.5,0.5,5.0])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(poly_svc.named_steps['svm_clf'].coef_)
print('模型截距')
print(poly_svc.named_steps['svm_clf'].intercept_)

• 输出显示：

4.2.2 高斯核

代码（续写在上面同一个项目里即可）：

#利用pipeline进行一体化编程，为了方便，将它放入函数中
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

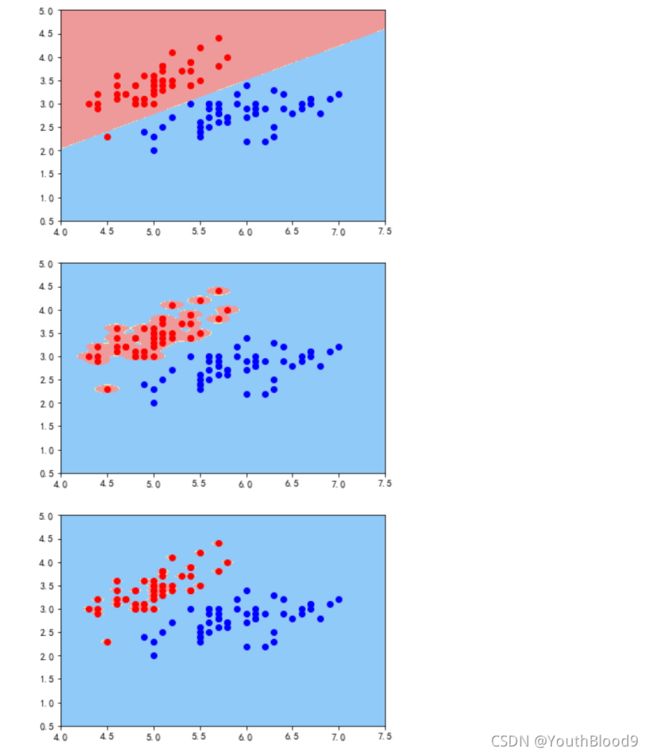
### 分别设置gamma=0.01、50、200
svc=RBFKernelSVC(gamma=0.01)#gamma参数很重要，gamma参数越大，支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[4.0,7.5,0.5,5.0])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

svc=RBFKernelSVC(gamma=50)#gamma参数很重要，gamma参数越大，支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[4.0,7.5,0.5,5.0])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

svc=RBFKernelSVC(gamma=200)#gamma参数很重要，gamma参数越大，支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[4.0,7.5,0.5,5.0])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

• 输出结果显示：
  

即验证了gamma参数越大，支持向量越小。

小小的总结

1. LDA优缺点

LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

• LDA算法的主要优点有：
  1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
  2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。
• LDA算法的主要缺点有：
  1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
  2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
  3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
  4）LDA可能过度拟合数据。

2. SVM的优点

1）不需要很多样本，不需要有很多样本并不意味着训练样本的绝对量很少，而是说相对于其他训练分类算法比起来，同样的问题复杂度下，SVM需求的样本相对是较少的。并且由于SVM引入了核函数，所以对于高维的样本，SVM也能轻松应对。
2）结构风险最小。这种风险是指分类器对问题真实模型的逼近与问题真实解之间的累积误差。
3）非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也叫惩罚变量）和核函数技术来实现，这一部分也正是SVM的精髓所在。

参考文献

1. 线性判别分析（LDA）——简书
2. 支持向量机（SVM）——原理篇
3. LDA与SVM实践（python实现）
4. 线性判别分析LDA原理总结，简书
5. 分类算法SVM（支持向量机)