生成专题1 | 图像生成评价指标 Inception Score （IS）

• 文章转自微信公众号：机器学习炼丹术
• 作者：陈亦新（欢迎交流共同进步）
• 联系方式：微信cyx645016617

1.1 感性理解

IS是Inception Score。

熵entropy可以被用来描述随机性：如果一个随机变量是高度可预测的，那么它就有较低的熵；相反，如果它是乱序随机的，那么它就是有较高的熵。这和训练分类网络所用的交叉熵是同一个道理。

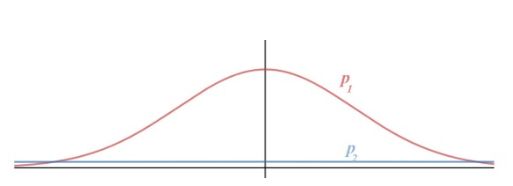
如下图，我们有两个概率：高斯分布和均匀分布。可以推断出，高斯分布的entropy小于均匀分布的entropy。高斯分布表明随机数是在0附近的

IS指标衡量的是生成模型的两个能力：

• 生成图片的质量；
• 生成图片的多样性。

我们定义$x$为生成图像，$y$为生成图像的判别器分类结果（以imagenet为例，那么是一个1000类别的分类）。

那么质量越高的图片，判别器分类的结果就会越确定。所以$P(y|x)$越确定，熵越小，那么图像质量越好。

之前我们的$x$可以理解为1张图片，那么$X$则是生成图片的集合，比方说随机生成了1000张图片的集合。

然后这1000个图片，都放到判别器当中判断类别。多样性最好的情况，就是每一个类别生成的图像数量相同。这个时候生成不同类别的概率相等，这个时候意味着熵最大（因为生成类别不确定）。

所以我们希望$p(y|x)$越小越好，质量越高；$p(y)$越大越好，多样性好。

1.2 数学推导

质量越高，$p(y|x)$的entropy越好。$p(y|x)$的entropy可以写成下面公式：

$-{\sum }_{i=1}^{m}p(y_i|x_i)\times log(p(y_i|x_i))$

其中m表示生成的图片数量。

而多样性越大越好，意味着$p(y)$的entropy越大，那么这个公式可写成：

$-{\sum }_{i=1}^{m}p(y_i)\times log(p(y_i))$

这里又要说一下KL散度了，这是描述两个分布距离的函数，在GAN当中用到了。

$KL(p(y|x),p(y))$

$={\sum }_{i=1}^{m}p(y_i|x_i)\times log(\frac{p(y_i|x_i)}{p(y_i)})$

$={\sum }_{i=1}^{m}p(y_i|x_i)\times log(p(y_i|x_i))$

$-{\sum }_{i=1}^{m}p(y_i|x_i)\times log(p(y_i))$

可以看到，这两分布的KL散度可以变成一个减法形式，前者是我们计算的描述图像质量的熵，我们后续就简单写成$-E(p(y|x))$

后者我们还得继续转换：
${\sum }_{i=1}^{m}p(y_i|x_i)\times log(p(y_i))$

$={\sum }_{i=1}^m\frac{p(y_i|x_i)}{p(y_i)}\times p(y_i)\times log(p(y_i))$

这个公式中，我们发现，跟描述生成多样性的熵有点类似了，就是多了一个$\frac{p(y_i|x_i)}{p(y_i)}$，要是这个等于1就好了。现在证明这个：

$\frac{p(y_i|x_i)}{p(y_i)}$

$=\frac{p(y_i，x_i)}{p(y_i)\times p(x_i)}$

$=\frac{p(y_i)\times p(x_i)}{p(y_i)\times p(x_i)}=1$

但是这里涉及一个假设，就是联合概率的变量互相独立。但是我们生成图像和类别明显是不独立的。这个问题就是IS的一个局限性。IS呢就是两个分布的KL散度。所以综上所示：

$KL(p(y|x),p(y))=-E(p(y|x))+E(p(y))$

所以KL散度越大，IS值越高，那么多样性熵就越大，质量熵越小，那么生成模型就越好。

1.3 KL散度的物理意义

KL散度是衡量两个分布之间的距离。

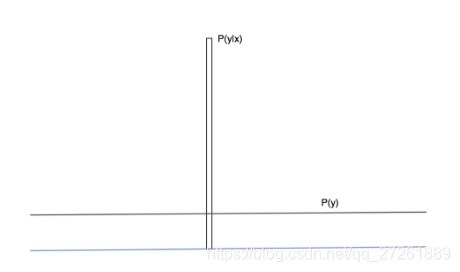
这个图中，我们希望条件概率$p(y|x)$是一个确定的数，那么可以理解为一个方差为0的高斯分布；
而另外的概率$p(y)$是一个均匀分布，那么就是方差无穷大的高斯分布。标准差的差异太大，所以不需要考虑均值的位置。所以我们可以从图中简单的看出来，这两个极端的高斯分布的距离越大，那么意味着模型的质量和多样性就会越好。

KL散度就刚好利用了生成网络当中的确定和不确定的两个部分。