基于粒子群算法优化BP神经网络的PID控制算法（Matlab代码实现)

欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

1 概述

     传统比例-积分-微分（Proportion Integral Derivative,PID）控制器存在参数整定困难，不能在线实时调整以及面对复杂非线性系统时应用效果不佳等问题，提出一种基于粒子群算法（Particle Swarm Optimization,PSO）优化的反向传播（Back Propagation,BP）神经网络PID控制方法。将BP神经网络与PID控制器相结合，利用BP神经网络的自适应学习能力在线实时调整PID控制参数，提升系统稳定性，针对BP-PID自学习过程中容易陷入局部极小值问题，利用改进的PSO算法对其进行优化，确保BP-PID系统收敛于全局最优解。基于仿真数据开展实验，结果表明，所提方法能够有效提升系统的控制精度和控制稳定度。 

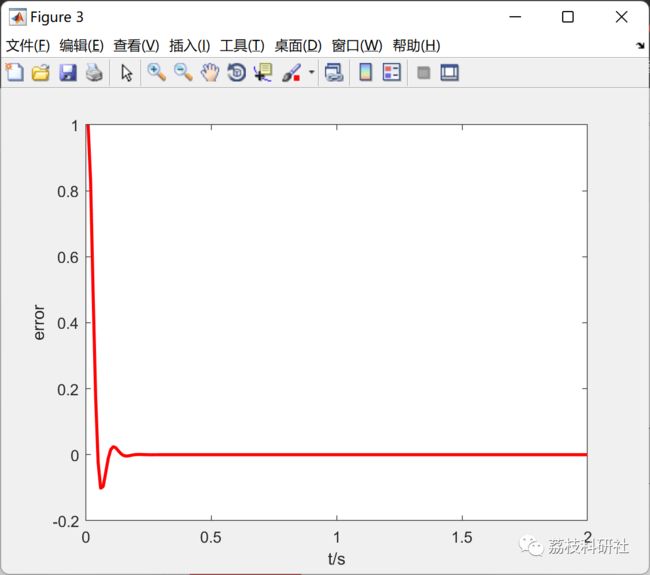
2 运行结果

部分代码：

function [wi_init, wo_init]=SPO_InitW()
%clear;
tic   %该函数表示计时开始
%神经网络参数
IN=4; H=5; Out=3;
%------给定初始化条件----------------------------------------------
c1=2;    %1.4962;             %加速常数
c2=2 ;   %1.4962;             %加速常数
%w=0.7298;              %惯性权重
Wmax=0.9 ;   Wmin=0.4;  %准备采用线性权重衰减法
MaxDT=50;            %最大迭代次数
D=(H*IN)+(Out*H); %搜索空间维数（测试函数sphere中未知数个数）
N=20;                      %初始化群体个体数目（ 一般20个粒子就足够）
Vmax=5;
Vmin=-5;
Pmax=5;
Pmin=-5;

%------初始化种群的个体(可以在这里限定位置和速度的范围)------------
for i=1:N
        x(i,:)=0.15*rands(1,D); 
        v(i,:)=0.15*rands(1,D); 
end

%------先计算各个粒子的适应度，并初始化个体最优位置y和全局最优位置Pg--------
for i=1:N
    p(i)=BPNN_Fitness(x(i,:)) ; %计算每个粒子适应度
    y(i,:)=x(i,:);         %初始化个体最优位置y为在时间步t=0时的粒子位置
end
Pg=x(1,:);              %Pg为全局最优位置 这里是初始化
for i=2:N
    if BPNN_Fitness(x(i,:))         Pg=x(i,:);          %更新全局最优位置 初始化完毕 
    end
end

%------进入主要循环，按照公式依次迭代，直到满足精度要求------------
for t=1:MaxDT
    fprintf('第%d次迭代-----\n',t);
    %fprintf('适应度=%f\n',Pbest(t));
    for i=1:N
        w=Wmax-(t-1)*(Wmax-Wmin)/(MaxDT-1);
        v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(Pg-x(i,:));
        v(i,find(v(i,:)>Vmax))=Vmax;    %不能超过最大速度
        v(i,find(v(i,:)         
        x(i,:)=x(i,:)+v(i,:);   %更新了每个粒子的位置
        x(i,find(x(i,:)>Pmax))=Pmax;
        x(i,find(x(i,:)         if BPNN_Fitness(x(i,:))             p(i)=BPNN_Fitness(x(i,:));     %更新适应度
            y(i,:)=x(i,:);      %更新个体最佳位置
        end
        if p(i)             Pg=y(i,:);          %每一次迭代结束后更新群体最佳位置
        end
    end
    Pbest(t)=BPNN_Fitness(Pg);     %保存每一代的群体最佳适应值
end
toc %该函数表示计时结束

%获得经粒子群算法优化的神经网络权值初始值
for t=1:H
       wi_init(t,:)=x(1,(t-1)*IN+1:t*IN);
end
for r=1:Out
       wo_init(r,:)=x(1, ( (IN*H+1)+(r-1)*H ): ( (IN*H+1)+r*H-1 ) );
end

%------最后给出计算结果--------
disp('*************************************************************')    
disp('最优适应函数最优位置为：')
for i=1:D
    fprintf('x(%d)=%s\n',i,Pg(i));
end
fprintf('最后得到的优化极值为：%s\n',BPNN_Fitness(Pg));
disp('*************************************************************')
disp('迭代分析结果')
fprintf('迭代次数：%d\n',MaxDT);

figure(1);
plot(Pbest,'Linewidth',2);
title( ['适应度曲线' ]);
grid on
xlabel('迭代次数');ylabel('适应度');

 

3 参考文献

[1]曾雄飞.基于粒子群算法优化BP神经网络的PID控制算法[J].电子设计工程,2022,30(11):69-73+78.DOI:10.14022/j.issn1674-6236.2022.11.015.

4 Matlab代码实现