基于麻雀搜索的PID神经网络解耦控制算法 - 附代码
基于麻雀搜索的PID神经网络解耦控制算法
文章目录
- 基于麻雀搜索的PID神经网络解耦控制算法
-
- 1.PID神经元网络结构
- 2.控制律计算
- 3.权值修正
- 4.控制对象
- 5.模型建立
- 6.基于麻雀搜索的PID神经网络解耦控制算法
- 7.算法结果:
- 8.参考文献:
- 9.Matlab代码
摘要:PID 神经元网络采用的学习算法是梯度学习法,初始权值随机得到,权值在学习过程中可能陷入局部最优值。采用麻雀搜索算法优化神经元网络初始权值。
1.PID神经元网络结构
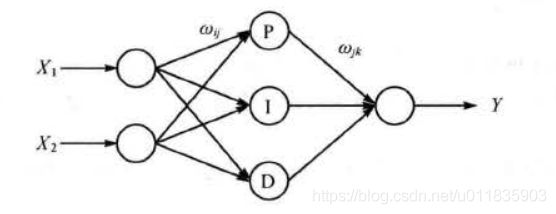
PID 神经元网络从结构上可以分为输入层、隐含层和输出层三层, n 个控制量的 PID 神经 元网络包含 n 个并列的相同子网络 , 各子网络间既相互独立 , 又通过网络连接权值相互联系。 每个子网络的输入层有两个神经元,分别接收控制量的目标值和当前值。每个子网络的隐含 层 由比例元、积分元和微分元构成,分别对应着 PID 控制器中的比例控制、积分控制和微分控制。 PID 神经元网络按被控系统控制量的个数可以分为控制单变量系统的单控制量神经元网 络和控制多变量系统的多控制量神经元网络。其中单控制量神经元网络是PID 神经元网络的基本形式,多控制量神经元网络可以看成是多个单控制量神经元网络的组合形式。单控制量神经元网络的拓扑结构如图1所示。
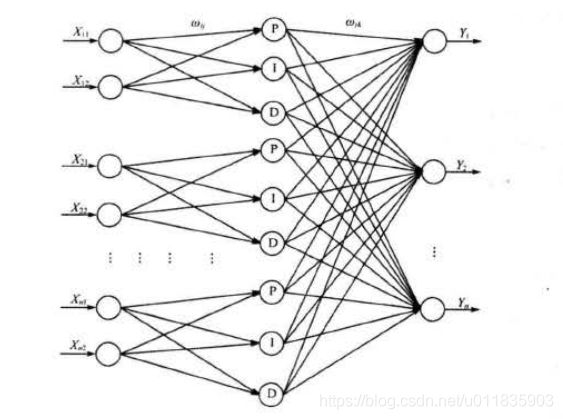
图 1中 X 1 X_1 X1是控制量的控制目标 , X 2 X_2 X2是控制量当前值 , Y Y Y 是神经元网络计算得到的控制律, w i j w_{ij} wij和 w j k w_{jk} wjk是网络权值,从中可以看到单控制量神经元网络是一个三层前向神经元网络,网络结构为 2-3- 1 ,隐含层包含比例元、积分元和微分元三个神经元。多控制量神经元网络可 以看成多个单控制量网络的并联连接,多控制量神经元网络拓扑结构如图 2 所示。图中, $X_{11} , X_{21} , … , X_{n1} $是控制量的控制目标 ; X 12 , X 22 , … , X n 2 X_{12} , X_{22} , …, X_{n2} X12,X22,…,Xn2 是控制量的当前值; Y 1 , . . , Y n Y_1,..,Y_n Y1,..,Yn是多控制量神经元网络计算得到的控制律 ; w i j w_{ij} wij和 w j k w_{jk} wjk是网络权值。
2.控制律计算
PID 神经元网络分为输入层、隐含层和输出层,网络输入量为控制量当前值和控制目标, 输出蛊为控制律,各层输入输出计算公式如下 。
(1) 输入层
输入层中包含2n个神经元,输出数据 x s i x_{si} xsi等于输入数据 X s i X_{si} Xsi 计算公式为:
x s i ( k ) = X s i ( k ) (1) x_{si}(k) = X_{si}(k) \tag{1} xsi(k)=Xsi(k)(1)
(2) 隐含层
隐含层有 3n 个神经元,包括 n 个比例神经元、n 个积分神经元和 n 个微分神经元。这些神经元的输入值相同,计算公式为 :
n e t i j ( k ) = ∑ i = 1 2 w i j x s i ( k ) , j = 1 , 2 , 3 (2) net_{ij}(k) = \sum_{i =1}^2 w_{ij}x_{si}(k),j = 1,2,3 \tag{2} netij(k)=i=1∑2wijxsi(k),j=1,2,3(2)
隐含层各神经元输出的计算公式如下:
比例神经元: u s 1 ( k ) = n e t s 1 ( k ) u_{s1}(k) = net_{s1}(k) us1(k)=nets1(k)
积分神经元: u s 2 ( k ) = n e t s 2 ( k ) + u s 2 ( k − 1 ) u_{s2}(k) = net_{s2}(k) + u_{s2}(k-1) us2(k)=nets2(k)+us2(k−1)
微分神经元: u s 3 ( k ) = n e t s 3 ( k ) − n e t s 3 ( k − 1 ) u_{s3}(k) = net_{s3}(k) - net_{s3}(k-1) us3(k)=nets3(k)−nets3(k−1)
式中 ,s 为并联子网络的序号; j为子网络中隐含层神经元序号, x s i ( k ) x_{si}(k) xsi(k) 为各子网络输入层神经元输出值 ; w i j w_{ij} wij为各子网络输入层至隐含层的连接权重值 。
(3)输出层
输出层有 n 个神经元 ,构成 n 维输出量,输出层的输出为隐含层全部神经元的输出值加权和,计算公式如下:
y h ( k ) = ∑ s = 1 n ∑ j = 1 3 w j k u s j ( k ) (3) y_h(k) = \sum_{s=1}^{n} \sum_{j=1}^3 w_{jk}u_{sj}(k) \tag{3} yh(k)=s=1∑nj=1∑3wjkusj(k)(3)
式中,h 为输出层神经元序号;s为子网的序号;j为子网的隐含层神经元序号 ; u s j ( k ) u_{sj}(k) usj(k)为隐含层各神经元输出值 ; w j k w_{jk} wjk为隐含层至输出层的连接权重值。
3.权值修正
PID 神经元网络在控制的过程中根据控制量误差按照梯度修正法修正权值,使得控制量不断接近控制目标值 ,权值修正的过程如下 。
误差计算公式如下:
J = ∑ E = ∑ k = 1 n [ y h ( k ) − r ( k ) ] 2 (4) J = \sum E = \sum_{k=1}^n[y_h(k) - r(k)]^2 \tag{4} J=∑E=k=1∑n[yh(k)−r(k)]2(4)
式中,n为输出节点个数, y h ( k ) y_h(k) yh(k)为预测输出; r ( k ) r(k) r(k)为控制目标。
PID神经元网络权值修正公式如下:
a.输出层到隐含层:
w j k ( k + 1 ) = w j k ( k ) − η δ J δ w j k (5) w_{jk}(k+1) = w_{jk}(k) - \eta\frac{\delta J}{ \delta w_{jk}} \tag{5} wjk(k+1)=wjk(k)−ηδwjkδJ(5)
b.输入层到输出层
w i j ( k + 1 ) = w i j ( k ) − η δ J δ w i j (6) w_{ij}(k+1) = w_{ij}(k) - \eta\frac{\delta J}{ \delta w_{ij}} \tag{6} wij(k+1)=wij(k)−ηδwijδJ(6)
其中 η \eta η为学习速率。
4.控制对象
PID 神经元网络的控制对象是一个 3 输入 3 输出的复杂耦合系统,系统的传递函数如下:
{ y 1 ( k ) = 0.4 ∗ y 1 ( k − 1 ) + u 1 ( k − 1 ) / [ 1 + u 1 ( k − 1 ) 2 ] + 0.2 u 1 ( k − 1 ) 3 + 0.5 u 2 ( k − 1 ) + 0.3 y 2 ( k − 1 ) y 2 ( k ) = 0.2 ∗ y 2 ( k − 1 ) + u 2 ( k − 1 ) / [ 1 + u 2 ( k − 1 ) 2 ] + 0.4 u 2 ( k − 1 ) 3 + 0.2 u 1 ( k − 1 ) + 0.3 y 3 ( k − 1 ) y 3 ( k ) = 0.3 ∗ y 3 ( k − 1 ) + u 3 ( k − 1 ) / [ 1 + u 3 ( k − 1 ) 2 ] + 0.4 u 3 ( k − 1 ) 3 + 0.4 u 2 ( k − 1 ) + 0.3 y 1 ( k − 1 ) (7) \begin{cases} y_1(k) = 0.4*y_1(k-1)+u_1(k-1)/[1+u_1(k-1)^2] + 0.2u_1(k-1)^3+0.5u_2(k-1)+0.3y_2(k-1)\\ y_2(k) = 0.2*y_2(k-1)+u_2(k-1)/[1+u_2(k-1)^2] + 0.4u_2(k-1)^3+0.2u_1(k-1)+0.3y_3(k-1)\\ y_3(k) = 0.3*y_3(k-1)+u_3(k-1)/[1+u_3(k-1)^2] + 0.4u_3(k-1)^3+0.4u_2(k-1)+0.3y_1(k-1)\\ \end{cases}\tag{7} ⎩⎪⎨⎪⎧y1(k)=0.4∗y1(k−1)+u1(k−1)/[1+u1(k−1)2]+0.2u1(k−1)3+0.5u2(k−1)+0.3y2(k−1)y2(k)=0.2∗y2(k−1)+u2(k−1)/[1+u2(k−1)2]+0.4u2(k−1)3+0.2u1(k−1)+0.3y3(k−1)y3(k)=0.3∗y3(k−1)+u3(k−1)/[1+u3(k−1)2]+0.4u3(k−1)3+0.4u2(k−1)+0.3y1(k−1)(7)
从式7中可以看出该系统的控制量相互搞合,用 一般的控制方法难以取得理想的控制效果。
5.模型建立
PID 神经元网络控制器和被控系统构成的闭环控制系统如图 3所示:
图中, r 1 , . . . , r n r_1,...,r_n r1,...,rn是控制量控制目标 , u 1 , . . . , u n u_1,...,u_n u1,...,un为控制器控制律, y 1 , . . . , y n y_1,...,y_n y1,...,yn为控制量当前值。对于本案例来说,由于被控对象有三个控制量,所以选择包含三个单神经元网络组成的多神经元网络作为系统控制器. 网络权值随机初始化,控制量初始值为[0,0,0],目标为[0.7,0.4,0.6],控制时间间隔为0.001s。
6.基于麻雀搜索的PID神经网络解耦控制算法
麻雀搜索算法的具体原理参考博客:https://blog.csdn.net/u011835903/article/details/108830958。
PID 神经元网络采用的学习算法是梯度学习法,初始权值随机得到,权值在学习过程中可能陷入局部最优值。采用麻雀搜索算法优化神经元网络初始权值。适应度函数即为控制误差和。
麻雀算法参数设置如下:
pop=50; % 种群数量
Max_iteration=40; % 设定最大迭代次数
dim = 3*6 + 3*9;% 权值维度
lb = -0.3;%上边界
ub = 0.3;%下边界
fobj = @(x) fun(x);%适应度函数
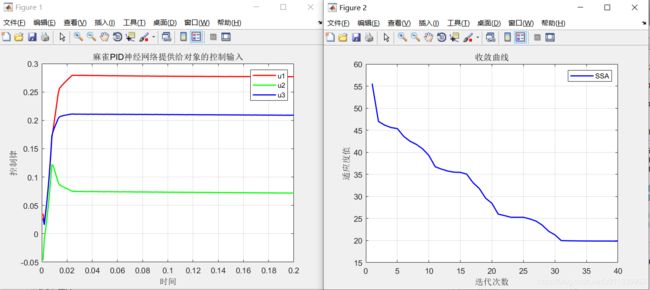
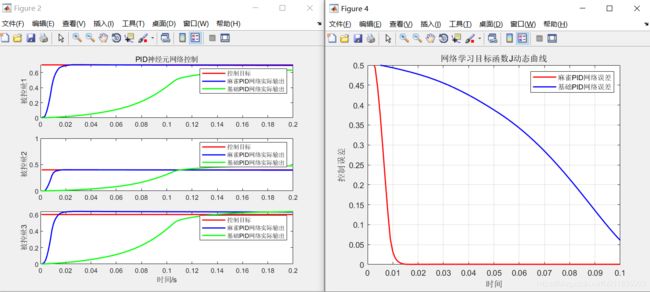
7.算法结果:
从结果上来看,改进后的麻雀算法收敛速度快,控制精度明显高于基础的PID网络,且控制时间明显优于基础PID网络误差。
8.参考文献:
书籍《MATLAB神经网络43个案例分析》,上文基本原理均摘自该书籍。
9.Matlab代码
个人资料介绍