基于遗传算法优化极限学习机预测及其MATLAB实现-附代码

基于遗传算法优化极限学习机预测及其MATLAB实现-附代码

1 极限学习机ELM原理

ELM预测相关理论可查看上一篇博客: 极限学习机ELM回归预测

简单的ELM预测代码如下:

%初始化
clear
close all
clc
warning off
rng('default')

P=randi([1 10],3,100);        %构建训练数据的输入样本
T=sum(P,1);           %构建训练数据的输出样本
P1= randi([1 10],3,10);     %构建测试数据的输入样本
T1=sum(P1,1);           %构建测试数据的输出样本

% 归一化...使用mapminmax函数即可，由于生成的数据无量纲和数量级差异，跳过

%% ELM训练过程
N=3;       %输入层的神经元节点个数
L=30;     %隐含层的神经元节点个数
M=1;     %输出层的神经元节点个数

IW=2*rand(L,N)-1;           %初始化输入层与隐含层的连接权值，范围(-1,1)
B=rand(L,1);             %初始化隐含层的偏置，范围(0,1)
tempH = IW * P + B;  %计算隐含层的输出值
h= 1./ (1 + exp(tempH ));          %使用映射函数G(x)=1/(1+exp(x))，h为隐含层对第样本特征的映射值
LW=pinv(h')*T';          %求逆，得到输出层的权值，结束训练（转置是为了让维度对应）

%% ELM预测过程
tempH1=IW*P1+B;         %计算隐含层输出值
h1= 1./ (1 + exp(tempH1 ));        %对特征作映射
ELM_OUT= (h1' * LW)';

%% 分析预测的误差
error=T1-ELM_OUT;   %误差=实际值-预测值
disp('          序号     期望值      预测值       误差')
disp([1:10
    T1
    ELM_OUT
    error]')
disp('误差平方和...')
sse=sum(error.^2)    
disp('均方误差...')
mse=mean(error.^2) 
disp('平均相对误差...')
mape=mean(abs(error)./T1)   

%作图分析预测的效果
figure
hold on
plot(1:10,T1,'bo:','linewidth',1.0)
plot(1:10,ELM_OUT,'r*-.','linewidth',1.0)
legend('期望值','预测值')
xlabel('测试样本序号')
ylabel('指标的值')

2 基于GA-ELM预测模型的建立

在理论与代码的实现过程中，注意到存在两个随机变量: 输入层与隐含层的连接权值IW，以及隐含层的阈值B.

IW=2*rand(L,N)-1;           %随机初始化权值，服从(-1,1)均匀分布
B=rand(L,1);             %随机初始化阈值，服从(0,1)均匀分布

针对ELM 随机产生的输入层权值和隐含层阈值导致网络不稳定的问题，采用遗传算法对极限学习机的权值和阈值进行优化，从而降低预测误差值，改善网络性能，得以提升ELM预测精度。

2.1 优化变量的处理

设极限学习机的输入层神经元节点数目为 $n$, 隐含层节点数目为 $l$,

输入层与隐含层的连接权值为 $\omega$:

$$\omega ={\left[\begin{array}{cccc}{\omega }_{11}& {\omega }_{12}& \cdots & {\beta }_{1n}\\ {\omega }_{21}& {\omega }_{22}& \cdots & {\beta }_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ {\omega }_{l1}& {\omega }_{l2}& \cdots & {\beta }_{ln}\end{array}\right]}_{l\times n}$$

隐含层的阈值为 $b$:

$$b={\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_l\end{array}\right]}_{l\times 1}$$

式中，$\omega 、b$分别为矩阵和列向量。使用遗传算法等智能算法求解时，对于优化变量，采用向量型编码个体位置的方法操作较为简单。此外，还有矩阵编码，二进制编码等编码方式。此处采用向量型的浮点编码。

做法是: 先确定$\omega$ 与 $b$中元素变量的总数: $n\times l+l$，再生成等长度的初始种群位置向量。由 $n$ 个个体组成的父代可表示如下:

$$X=\left[\begin{array}{cccc}{x}_1^1& x_1^2& \dots & x_1^d\\ x_2^1& x_2^2& \dots & x_2^d\\ \dots & \dots & \dots & \cdots \\ x_n^1& x_n^2& \dots & x_n^d\end{array}\right]$$

式中, d是变量维度, 且 $d=n\times l+l$.

2.2 目标函数的处理

根据ELM的训练公式:

$$\Vert \mathbf{H}\mathbf{\beta }-\mathbf{T}{\Vert }^2=0$$

对上式求逆，解出输出层的权值 $\beta$，可得到一个训练好的极限学习机模型。因而当该方程可解 ($H$的逆矩阵存在) 时，得到的模型对训练样本是无误差的。GA优化目的是针对随机初始化权值阈值带来的网络预测不稳定，通过优化权值和阈值，提升预测精度。因此，将训练集与测试集整体的均方误差作为适应度函数。适应度函数值越小，表明训练越准确，且兼顾模型的预测精度更好。

$$F=\min \left(MS{E}_{\text{Trainingset },\text{ Testingset }}\right)$$

式中，TraingingSet，TestingSet，分别为训练集和测试集的样本。

2.3 流程图设计

3 基于GA-ELM模型的身体脂肪预测应用

3.1 数据介绍

身体脂肪数据集 bodyfatDataset 是深度学习中常用的预测数据集，对该数据集的描述如下:

bodyfatInputs - a 13x252 matrix defining thirteen attributes for 252
people.
  1. Age (years)
  2. Weight (lbs)
  3. Height (inches)
  4. Neck circumference (cm)
  5. Chest circumference (cm)
  6. Abdomen 2 circumference (cm)
  7. Hip circumference (cm)
  8. Thigh circumference (cm)
  9. Knee circumference (cm)
 10. Ankle circumference (cm)
 11. Biceps (extended) circumference (cm)
 12. Forearm circumference (cm)
 13. Wrist circumference (cm)

bodyfatTargets - a 1x252 matrix of associated body fat percentages,
to be estimated from the inputs.

整理到EXCEL中, 数据形式如下:

样本序号	输入指标1	输入指标2	…	输出指标
1	-	–	–	–
2	-	–	–	–
…	-	–	–	–
n	-	–	–	–

3.2 数据处理

由于不同变量的单位和取值范围差异较大，为了消除变量之间数量级的差别避免造成预测误差，以及方便求解，将数据进行归一化处理是实现预测前对数据常做的处理。采用MATLAB 自带归一化函数mapmin max 将所有数据都转化为［－ 1，1］之间的数据。函数调用方式如下:

［pn，ps］ = mapminmax( p) 

式中, p是输入原始数据， pn 是归一化的数据， ps是记录数据归一化操作的结构体。输出数据的归一化同理，预测完成后同样利用此函数进行反归一化，获得真实数据。

3.3 GA-ELM预测算法的步骤

1. 初始化染色体种群编码。将极限学习机的输入层权值与隐含层阈值元素取出，并计算染色体长度。随机初始化染色体。
2. 设置适应度函数。利用ELM对样本的预测输出误差作为适应度函数，计算初始种群中个体的适应度值。
3. 进行选择、交叉、变异操作。采用轮盘赌选择时，对于适应度函数，由于取的是均方误差，在进化过程中，均方误差减小，因此轮盘赌设计时适应度函数需取倒数，从而选择"适应度大"的个体。
4. 计算子代个体的适应度，并与父代个体合并，留下适应度值较好的个体构成新的子代种群。
5. 反复迭代执行3和4步，直到迭代次数达到设定的最大值。
6. 输出最好的染色体信息。对适应度值最好的染色体进行解码，并将解码后得到的权值和阈值赋给预测使用的ELM。
7. 以最优的权值和阈值初始化ELM 的参数，获得最优的网络结构。最后测试网络的预测精度。

3.4 组合模型的参数设置

确定ELM的结构参数:

% 1. 输入层神经元节点数,
inputnum=size(input,2);  % input的行向对应输入指标个数

% 2. 输出层的神经元节点数,
outputnum=size(output,2);  % output的行向对应输出指标个数

disp('/')
disp('极限学习机ELM结构...')
disp(['输入层的节点数为：',num2str(inputnum)])
disp(['输出层的节点数为：',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')

% 3. 确定隐含层的神经元节点个数
%注意：BP神经网络确定隐含层节点的方法是：采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
%在极限学习机中，该经验公式往往会失效，设置较大的范围进行隐含层节点数目的确定即可。

MSE=1e+5; %初始化最小误差
for hiddennum=20:30                      
...
%更新最佳的隐含层节点
    if minMse<MSE
        MSE=minMse;
        hiddennum_best=hiddennum;
    end

初始化遗传算法的参数:

nvars=inputnum*hiddennum_best+hiddennum_best;    %自变量个数
PopulationSize_Data=30;   %种群规模
MaxGenerations_Data=50;   %最大进化代数
CrossoverFraction_Data=0.8;  %交叉概率
MigrationFraction_Data=0.2;   %变异概率

4 运行结果

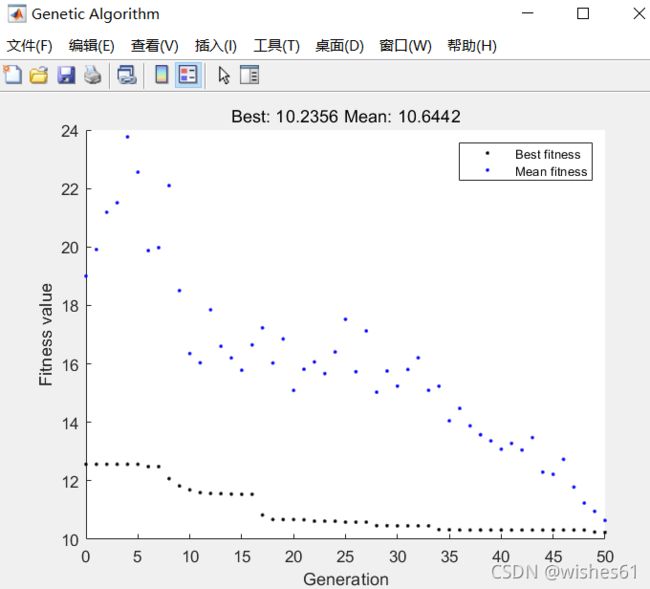
4.1 GA的进化曲线，含最优的适应度值与平均适应度

4.2 GA优化ELM预测的结果与误差分析

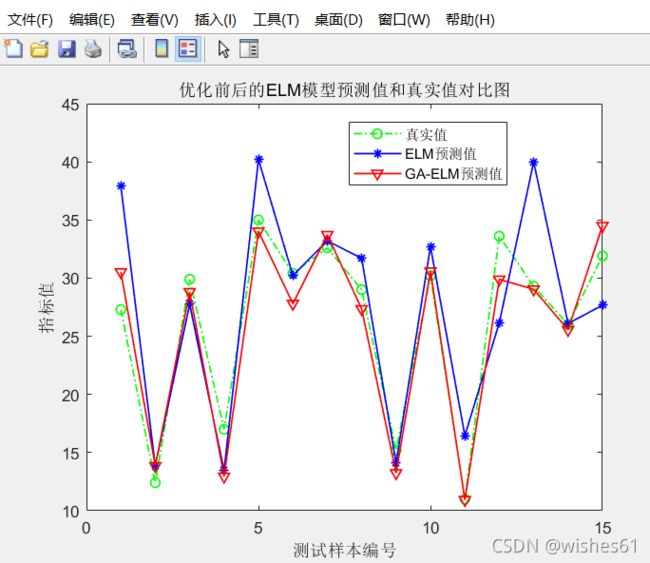
4.3 优化前后的预测曲线对比 (绿色为实测值, 红色为GA-ELM预测值, 蓝色为ELM预测值)

5 MATLAB代码

见博客主页