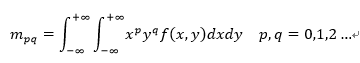图像特征(二)——形状特征(主轮廓特征、区域特征、图像的矩及Hu矩)

转载请注明出处 https://mp.csdn.net/console/editor/html/105172749

接续上一节内容(颜色特征)，本文主要介绍形状特征，并给出matlab上实现的demo。

形状特征

        形状特征有两类表示方法，一类是轮廓特征，一类是区域特征。图像的轮廓特征主要针对物体的外边界；而图像的区域特征则关系到整个形状区域。下面将介绍几种典型的形状特征描述方法：

轮廓特征

        轮廓是一系列相连的点组成的曲线，代表了物体的基本外形。其与边缘的不同：(1)轮廓是连续的，边缘并不全都连续；(2)边缘主要作为图像的物体特征；而轮廓主要用来分析物体的形态(如周长和面积)；(3)边缘包括轮廓。一般在二值图像中寻找轮廓，寻找轮廓是针对白色物体，即物体是白色，而背景是黑色。

1 边界特征法

        通过对边界特征的描述来获取图像的形状参数。其中Hough变换检测平行直线和边界方向直方图方法是经典方法。

Hough变换是利用图像全局特性而将边缘像素连接起来，组成区域封闭边界的一种方法，其基本思想是点-线的对偶性。

边界方向直方图：首先微分图像求得图像边缘，2）做出关于边缘大小和方向的直方图，通常的方法是构造图像灰度梯度方向矩阵。

2 傅里叶形状描述符法

         傅里叶形状描述符(Fourier shape deors)基本思想是用物体边界的傅里叶变换作为形状描述，利用区域边界的封闭性和周期性，将二维问题转换为一维问题。

        由边界点导出三种形状表达：曲率函数、质心距离、复坐标函数。

区域特征

1 几何参数法

        形状的表达和匹配采用更为简单的区域特征描述方法，如采用有关形状定量测量(如矩、面积、周长等)的形状参数法。——具体看后文——矩的介绍。

       需要说明的是：形状参数的提取，必须以图像处理及图像分割为前提，参数的准确性必然受到分割效果的影响，对分割效果很差的图像，形状参数甚至无法提取。

2 形状不变矩法—区域特征

     利用目标所占区域的矩作为形状描述参数。

其他

       近年来，在形状的表示和匹配方面的工作还包括有限元法(Finite Element Method, FEM)、旋转函数(Turning)和小波描述符(Wavelet Deor)等方法。

基于形状特征检索的共同问题

1. 目前基于形状的检索方法缺乏比较完善的数学模型；
2. 目标有变形时，检索结果不太可靠；
3. 许多形状特征仅描述了目标局部的性质，要全面描述目标对计算时间和存储量有较高的要求；
4. 许多性质特征反映的目标形状信息与人的直观感受不完全一致。

图像的矩(Image Moments)

1 矩的介绍

        矩用来抽取图像(块)的特征。图像中，低阶矩反映低频(主要的)信息，高阶矩反映高频(细节)信息。从一幅图像计算出来的矩集，不仅可以描述图像形状的全局特征，还可以提供大量关于该图像不同的几何特征信息，如大小、位置、方向和形状等。矩函数在图像分析中有广泛应用，如模式识别、目标分类、目标识别与方位估计等。

       普通矩的计算：

                         

      图像矩的计算，是普通矩的离散化。对于强度为fx,y 的像素点，(p+q) 阶矩可定义为：

                         

      其中，C与R分别表示图像的列与行。

各阶矩的物理意义与计算：

1. 0阶矩(m00 )：目标区域的面积(质量)；
2. 1阶矩((m01,m10 )：目标区域的质心；
3. 2阶矩(m20,m02,m11 )：目标区域的旋转半径；
4. 3阶矩(m30,m03,m12,m21 )：目标区域的方位和斜度，反映目标的扭曲。

2 中心矩：构造平移不变性

        以目标区域的质心为中心构建中心矩，那么矩的计算永远是目标区域中的点相对于目标区域的质心，而与目标区域的位置无关，即具备了平移不变性。

      目标区域的质心坐标：

                   

       根据求得的质心坐标，可以构造出中心距：

                 

3 归一化中心矩：构造尺度不变性

        为抵消尺度变化对中心矩的影响，利用零阶中心矩u00 对各阶中心矩进行归一化处理，得到归一化中心矩：

               

       零阶矩表示目标区域的质量(面积)，如果目标区域的尺度发生变化，其零阶中心距也会相应发生改变，使得矩具备尺度不变性。

​​​​​​​4 Hu矩：构造旋转不变性

       利用二阶和三阶规格中心距可推导出以下7个不变矩组(Φ1 ~Φ7 )，他们在图像平移、旋转和比例变化时保持不变。

      Φ1=η20+η02

      Φ2=(η20-η02)2+4η112

      Φ3=(η30-3η12)2+(3η21-η03)2

      Φ4=(η30+η12)2+(η21+η03)2

      Φ5=η30-3η12η30+η12η30+η122-3η21+η032+3η21-η03η21+η033η30+η122-η21+η032

      Φ6=η20-η02η30+η122-η21+η032+4η11(η30+η12)(η21+η03)

      Φ7=3η21-η03η21+η03η30+η122-3η21+η032-η30-3η12η21+η033η30+η122-η21+η032

具体实现代码

function n = FcnHuSquare( oriImg )
[m,n,~] = size(oriImg);


% 图像灰度化

grayImg = rgb2gray(oriImg);


% canny边缘检测提取边缘,保留边缘灰度图像
edgeImg = edge( grayImg, 'canny' );
zerosIndex =  edgeImg==0 ;
grayImg(zerosIndex)=0;

% 图像二值化
bwImg = zeros( m,n );
level = graythresh(grayImg);
thresh = level*255;
onesIndex =  grayImg>=thresh ;
bwImg(onesIndex) = 1;


%% 计算图像质心

m00 = sum( sum(bwImg) );  % 零阶矩
m01 = 0;                  % 一阶矩的初值
m10 = 0;                  % 一阶矩的初值
for i = 1:m
    for j = 1:n
        m01 = bwImg(i,j)*j + m01;
        m10 = bwImg(i,j)*i + m10;
    end
end
I = m10/m00;
J = m01/m00;

% 计算图像中心矩
u11 = 0;
u20 = 0; u02 = 0;
u30 = 0; u03 = 0;
u12 = 0; u21 = 0;
for i = 1:m
    for j = 1:n
        u11 = bwImg(i, j)*(i-I)*(j-J) + u11;
        u20 = bwImg(i, j)*(i-I)^2 + u20;
        u02 = bwImg(i, j)*(j-J)^2 + u02;
        u30 = bwImg(i, j)*(i-I)^3 + u30;
        u03 = bwImg(i, j)*(j-J)^3 + u03;
        u21 = bwImg(i, j)*(i-I)^2*(j-J) + u21;
        u12 = bwImg(i, j)*(i-I)*(j-J)^2 + u12;
    end
end
u20 = u20/(m00^2);
u02 = u02/(m00^2);
u11 = u11/(m00^2);
u30 = u30/(m00^(5/2));
u03 = u03/(m00^(5/2));
u12 = u12/(m00^(5/2));
u21 = u21/(m00^(5/2));

% 7个Hu不变矩
n(1) = u20 + u02;
n(2) = (u20-u02)^2 + 4*u11^2;
n(3) = (u30-3*u12)^2 + (3*u21-u03)^2;
n(4) = (u30+u12)^2 + (u21+u03)^2;
n(5) = (u30-3*u12)*(u30+u12)*( (u30+u12)^2-3*(u21+u03)^2 ) + ...
       (3*u21-u03)*(u21+u03)*( 3*(u30+u12)^2-(u21+u03)^2 );
n(6) = (u20-u02)*( (u30+u12)^2-(u21+u03)^2 ) + 4*u11*(u30+u12)*(u21+u03);
n(7) = (3*u21-u03)*(u21+u03)*( (u30+u12)^2-3*(u21+u03)^2 ) - ...
       (u30-3*u12)*(u21+u03)*( 3*(u30+u12)^2-(u21+u03)^2 );

end