频繁项集算法
目录
编辑
前言
基础知识
正文
一、Apriori算法
二、FP-Tree算法
1)第一次扫描数据对1-项集进行计数:
2)建立FP-Tree
3)FP-Tree获取频繁项集
总结
前言
频繁项集挖掘是数据挖掘研究课题中一个很重要的研究基础,它可以告诉我们在数据集中经常一起出现的变量,为可能的决策提供一些支持。频繁项集挖掘是关联规则、相关性分析、因果关系、序列项集、局部周期性、情节片段等许多重要数据挖掘任务的基础。因此,频繁项集有着很广泛的应用,例如:购物篮数据分析、网页预取、交叉购物、个性化网站、网络入侵检测等。
基础知识
如超市中的物品支持表格:
| 用户 | 辣条(A) | 可乐(B) | 铅笔(C) | 羽毛球(D) | 洗衣液(E) |
| 1 | √ | √ | √ | ||
| 2 | √ | √ | √ | √ | |
| 3 | √ | √ | √ | ||
| 4 | √ | √ | √ | ||
| 5 | √ | √ |
支持度:单个项占总项集的百分比,比如辣条的支持度=4/5*100%=80%,可乐的支持度=3/5*100%=60%。
置信度:辣条>=羽毛球的置信度=3/4*100%=75%,可乐>=羽毛球的置信度=3/3*100%=100%。
项集:最基本的模式是项集,它是指若干个项的集合。
频繁模式:指数据集中频繁出现的项集、序列或子结构。
频繁项集:指支持度大于等于最小支持度(min_sup)的集合。其中支持度是指某个集合在所有事务中出现的频率。频繁项集的经典应用是购物篮模型。
正文
一、Apriori算法
假设minsupport=0.2,得出频繁项集:
1)1-项集C1={A,B,C,D,E},1-频繁项集L1={A,B,C,D};
2)1-频繁项集进行拼接得到2-项集C2={(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)},2-频繁项集L2={(A,B),(A,C),(A,D),(B,D),(C,D)};
3)2-频繁项集拼接得到3-项集C3={(A,B,C),(A,B,D),(A,C,D),(B,C,D)},3-频繁项集L3={(A,B,D)};
4)最后得到所有的频繁项目集L={(A,B),(A,C),(A,D),(B,D),(C,D),(A,B,D)}。
假设 minconfidence =60%,得出关联规则:
我们这里仅仅对最大的频繁项集(B,C,D)进行计算,得出其中是否有强关联规则:
B>=CD,confidence=33%,不是强关联规则;BC>=D,confidence=100%,强关联规则;
C>=BD,confidence=33%,不是强关联规则;CD>=B,confidence=50%,不是强关联规则;
D>=BC,confidence=25%,不是强关联规则;BD>=C,confidence=33%,不是强关联规则。
二、FP-Tree算法
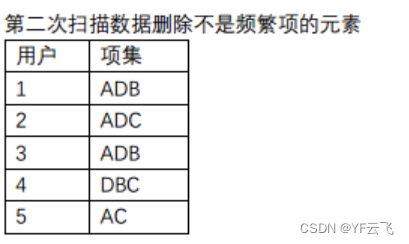
1)第一次扫描数据对1-项集进行计数:
我们仍然选用上面的例子,用户1:ABD,用户2:ACDE,用户3:ABD,用户4:BCD,用户5:AC
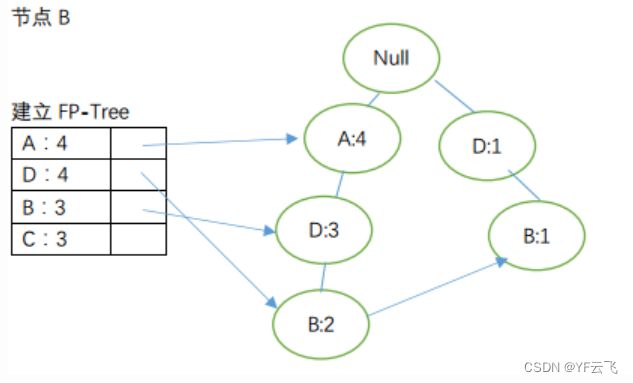
2)建立FP-Tree
至此,我们完成对FP-Tree的构建。
3)FP-Tree获取频繁项集
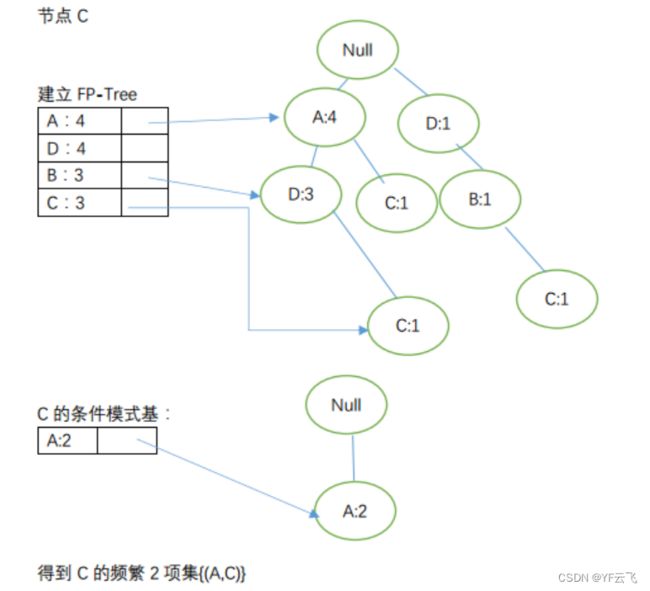
由节点从下到上依次获取频繁项:
其实上述中{(C,D)}的FP-Tree分别出现了2次,我们可得出其为频繁2-项集,则有C的到的频繁项2-项集:{(A,C),(C,D)};
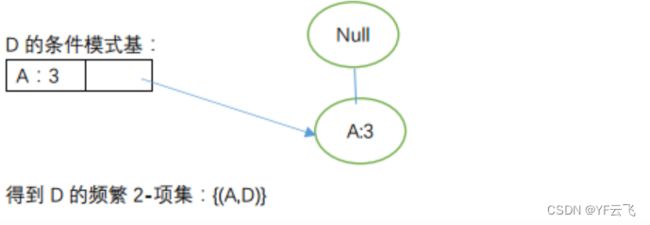
节点D
综上可知,所有的频繁项为:{(A,B),(A,C),(A,D),(B,D),(C,D),(A,B,D)}。
总结
1.对频繁项集挖掘算法进行研究的方向大概可归纳为以下四个方面:
a、在遍历方向上采取自底向上、自顶向下以及混合遍历的方
b、在搜索策略上采取深度优先和宽度优先策
c、在项集的产生上着眼于是否会产生候选项集;
d、在数据库的布局上,从垂直和水平两个方向上考虑数据库的布局。
2.对于不同的遍历方式,数据库的搜索策略和布局方式将会产生不同的方法,研究表明,没有什么挖掘算法能同时对所有的定义域和数据类型都优于其他的挖掘算法,也就是说,对于每一种相对较为优秀的算法,它都有它具体的适用场景和环境。