机器学习 —— 线性回归 简单使用

1、原理

分类的目标变量是标称型数据，而回归将会对连续型的数据做出预测。

应当怎样从一大堆数据里求出回归方程呢？

假定输入数据存放在矩阵X中，而回归系数存放在向量W中。那么对于给定的数据X1, 预测结果将会通过

Y=X*W

给出。现在的问题是，手里有一些X和对应的Y,怎样才能找到W呢？

一个常用的方法就是找出使误差最小的W。这里的误差是指预测Y值和真实Y值之间的差值，使用该误差的简单累加将使得正差值和负差值相互抵消，所以我 们采用平方误差。

最小二乘法

平方误差可以写做:

对W求导，当导数为零时，平方误差最小，此时W等于：

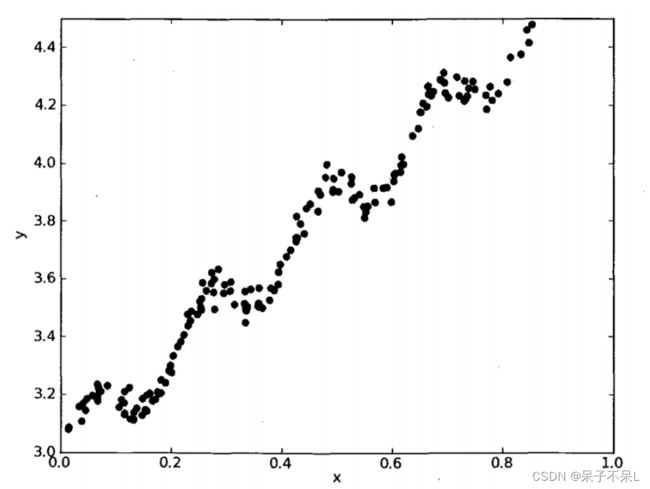
例如有下面一张图片：

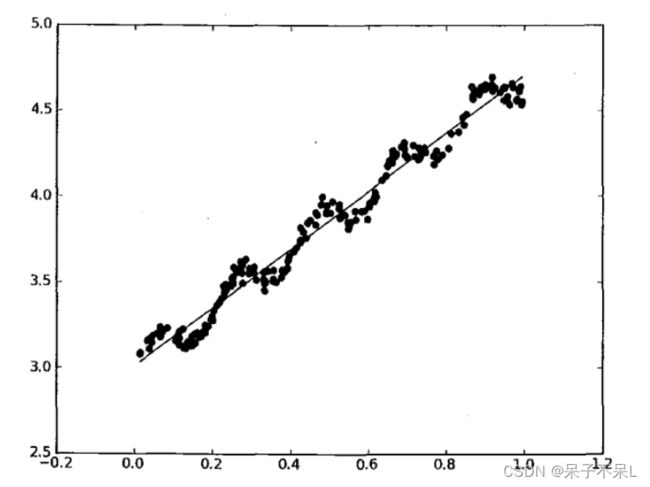
求回归曲线，得到：

2、实例

导包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

获取糖尿病数据

• from sklearn.datasets import load_diabetes
• load_diabetes()

from sklearn.datasets import load_diabetes


load_diabetes(return_X_y=True)

diabetes = load_diabetes()
data = diabetes['data']
target = diabetes['target']
feature_names = diabetes['feature_names']


df = pd.DataFrame(data,columns=feature_names)

df.shape   # (442, 10)

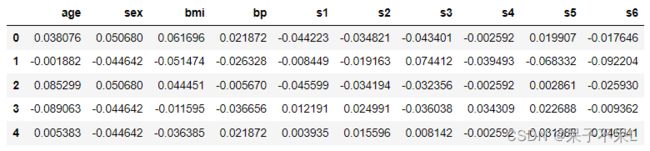
df.head()

抽取训练数据和预测数据

• from sklearn.model_selection import train_test_split

from sklearn.model_selection import train_test_split


x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2)
x_train.shape, x_test.shape

# ((353, 10), (89, 10))

创建模型

• 线性回归 from sklearn.linear_model import LinearRegression

# linear_model: 线性模型
from sklearn.linear_model import LinearRegression


linear = LinearRegression()
linear.fit(x_train,y_train)


y_pred = linear.predict(x_test)
y_pred

'''
array([146.65212544, 176.78286631, 116.92985898, 159.55409976,
       193.85883607, 135.41106111, 280.70084436, 203.82163258,
       165.95533668, 174.49532122, 146.50691274, 246.79656369,
       190.02124521,  76.94297194, 204.78399681, 193.80619254,
       227.51679413, 128.10670326,  71.63430601, 135.24501663,
        84.8203591 , 202.92275617, 138.08485679,  61.69447851,
        96.36845411, 164.15520646, 212.70460348, 204.9474425 ,
        84.9756637 , 173.57436885, 166.87931246, 134.35405336,
       129.06945724, 247.31336989, 231.07729133, 165.65216446,
       122.28042538, 152.78043098, 117.04854699, 210.760299  ,
       111.26588538, 160.47649157, 113.72698884, 119.07432727,
       208.73809232, 163.58086977, 233.74877671, 261.65461655,
        94.27924168,  99.33356167,  76.9808729 , 202.81604296,
       201.6140912 , 209.95385159, 132.67563341, 226.43697618,
       233.44881716, 120.34938632, 159.59745514, 289.03866456,
        92.42628632, 143.79779207, 185.67304201, 181.89096809,
       199.96572102,  82.5740475 , 164.51014764,  48.26282035,
       126.73251427, 125.36642402,  79.70522412, 156.80832312,
       204.06703941,  82.38532984,  72.58692041, 227.5553507 ,
       246.16425838, 147.21740976, 102.33611539,  57.14514311,
        57.10865057,  69.17398539, 126.62260931,  46.22527464,
       155.37162955, 201.76323199, 261.5957024 , 124.2167402 ,
       147.37497822])
'''


# 回归算法的 score 得分都比较低
linear.score(x_test,y_test)

# 0.44507903707232443

metrics: 评估

• mean_squared_error ： 均方误差
  • from sklearn.metrics import mean_squared_error as mse

# metrics ：评估
# mean_squared_error ：平均 平方 误差   均方误差
from sklearn.metrics import mean_squared_error as mse


# y_true : 测试集的真实结果
# y_pred : 测试集的预测结果
mse(y_test,y_pred)

# 2753.861377244474

求线性方程: y = WX + b 中的W系数和截距b

# 系数
linear.coef_

'''
array([  29.88001718, -168.98161514,  551.47482898,  299.75151839,
       -806.92788599,  479.3588313 ,  174.77682914,  241.53847521,
        769.4939919 ,   70.42616632])
'''

# 截距
linear.intercept_

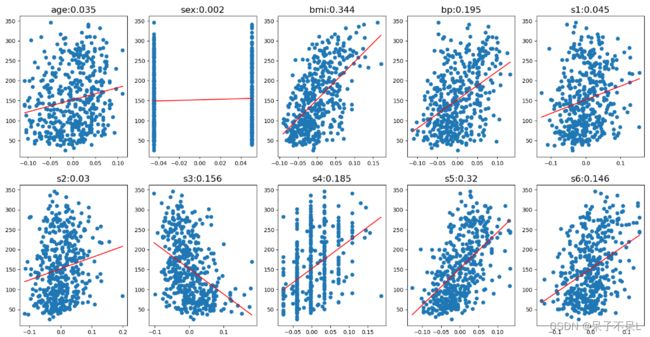
# 151.94208269059612

研究每个特征和标记结果之间的关系.来分析哪些特征对结果影响较大

# 2行5列
plt.figure(figsize=(5*4,2*5))

for i,col in enumerate(df.columns):
    # 一列数据
    data = df[col].copy()
    
    # 散点图
    axes = plt.subplot(2,5,i+1)
    axes.scatter(data,target)
    
    # 训练
    liner = LinearRegression()
    linear.fit(df[[col]],target)
    
    # 系数w
    w = linear.coef_[0]   # coef_ 返回列表
    
    # 截距
    b = linear.intercept_
    
    # 线性方程：y = wx + b
    x = np.array([data.min(),data.max()])
    y = w * x + b
    
    # 画直线
    axes.plot(x,y,c='r')
    
    # 求训练集得分
    score = linear.score(df[[col]],target)
    
    axes.set_title(f'{col}:{np.round(score,3)}',fontsize=16)