Generating Adversarial Examples with Adversarial Networks 采用GAN的方法来生成对抗样本

AdvGAN
论文地址：https://arxiv.org/abs/1801.02610
论文的内容：采用GAN的方式来生成对抗样本

啥是对抗样本

对抗样本：adversarial examples
就是在真实样本的基础上加上一点点扰动，通常人眼无法察觉，但机器学习分类算法却会误判为其他类别～～
eg：大熊猫 + 很小的扰动量 ----结果判决成了长臂猿
最右边的图就是对抗样本。人眼看上去还是大熊猫，但是机器学习算法却分类错误。

数学描述
$min||x_{adv}-x||,s.t.F(x_{adv})\ne y$
其中 $x$是真实样本，其类别是$y$.$F$是一个已经训练好的分类器网络。$x_{adv}$就是对抗样本。最小化扰动量（两者的差异），使得分类器判决错误。
分类：
根据对抗样本的输出是否确定了类别：

• 有目标对抗—指定$F(x_{adv})=y_{target}\ne y$
• 无目标对抗—只要分类错误就行$F(x_{adv})\ne y$

根据对攻击网络$F$的先验知识已知多少：

• 白盒对抗—需要知道网络的损失函数、梯度等
• 黑盒对抗—不需要网络内部知识

传统的对抗样本生成方法

大致分类：

1. 基于梯度的方法
   代表论文：
   [1] Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. ICLR 2015
   [2] Kurakin A, Goodfellow I, Bengio S. Adversarial examples in the physical world. ICLR 2017
   基本思路：把扰动加在梯度增加的方向，使得模型误判
2. 基于优化的方法
   代表论文：
   [3] Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks
   [4] Nicholas Carlini, David Wagner. Towards evaluating the robustness of neural networks. 2017 IEEE Symposium on Security and Privacy (SP)
   基本思路：求解优化问题，用各种变化方法使得优化问题好求解

缺点：
梯度方法快，但是不能保证对抗攻击有效
优化方法慢，一次只能对一个样本来优化

用GAN来生成对抗样本

推荐这篇blog来了解GAN，讲的非常好
https://blog.csdn.net/baidu_41867252/article/details/90369304

GAN是一种生成算法，目前在样本增强上有很多应用。
基本思路很简单：用噪声作为输入，送给生成器G，产生了虚假样本。（怎样使得虚假样本和真实样本很像呢，传统的方法可能是最小化二者之间的某种差别。）这里引入一个新的判决器网络D。G和D都是需要训练的，采用博弈的方法来交替训练二者，使得G不断强大，最后能够隐式的学习到真实样本的分布，从而产生和真实样本非常接近的样本。

为什么在图像生成中用GAN？
传统方法让真实图像和生成图像在像素级别上误差最小，实际上两个图像差一些像素对于整体而言没什么大影响，GAN是保证了整图级别上的相似。
eg：MNIST数据集中的2，如果拖尾写的长一点，仍然是个2，像素上差别是有的，但是不影响它是个2

回到对抗样本生成
用GAN来生成对抗样本，其实就是在原来GAN结构上增加了一个分类器网络$F$
原来的GAN网络：用于生成对抗样本，使得对抗样本和真实图像非常像（保证对抗样本和真实样本在视觉上无差别）
新增加的网络$F$:就是要攻击的分类器网络，用于判断生成的样本是否能够有效攻击，把损失函数传递给G和D用于训练。

结构图就是这样：

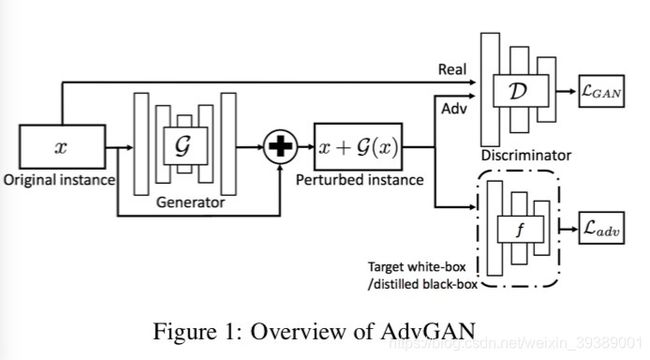
和原始的GAN有两个差别
1是增加了分类器网络$F$
2是原来的GAN的生成G的输入是噪声$z$，输出图像$G(z)$
这里用原始样本$x$作为输入，生成的是扰动量$G(x)$,生成的对抗样本$x_{adv}=x+G(x)$

训练使用如下损失函数
$L=L_{adv}^F+\alpha L_{GAN}+\beta L_{hinge}$
其中$\alpha ,\beta$是权重
$L_{adv}^F$是对抗样本在分类器上的损失函数，定义为
$L_{adv}^F=E_x[l_F(x+G(x),t)]$ 其中$t$是目标分类标签，就是上面的$y_{target}$，希望对抗样本$x+G(x)$能够被$F$分类为$t$,$l$就是在训练分类器网络$F$时候采用的loss，（例如交叉熵损失函数）。
可见在训练G的时候，还是需要$F$的损失函数信息，不过论文指出，当训练好了$G$之后，就可以利用$G$来生成对抗样本了，生成的时候就不需要$F$的信息了，因此相比于原来的白盒攻击，这是一种半白盒攻击（semi-white box attack）
而且生成时候可以大批量的生成样本哦，速度很快的哦～～～

还有一个loss是$L_{hinge}=E_x[max\{0,||G(x)|{|}_2-c\}]$，其中G(x)就是扰动量，这是为了约束扰动量的$L_2$范数不要超过一个给定的上限$c$。

用这个网络来训练G和D，达到均衡时候，把G拿出来用就可以啦！

黑盒攻击

传统的黑盒攻击方法依赖于模型的迁移特性，一般是先训练一个local模型，（其实是替代模型），然后根据local模型来生成对抗样本，希望这些对抗样本在真的黑盒模型上依然有效。

本文提出的方法不需要依赖迁移特性

1. 静态蒸馏 Static Distillation
   对于未知的黑盒模型b，训练一个蒸馏网络f
   需要随机的访问一些模型的输入和输出
   $argmi{n}_f{E}_x[H(f(x),b(x))]$
   其中，$H$是交叉熵，希望输入x之后，f网络和b网络的输出之间的交叉熵最小，以此来训练f。

2. 动态蒸馏 Dynamic Distillation
   静态方法的缺点：对抗样本在训练集合中未出现过，只是在预测阶段才有的。所以不清楚在对抗样本集合上面f和b究竟有多接近？？（不是很理解这个）
   解决方法：动态的访问，联合训练f和G

算法描述：
迭代：

1. 固定$f_{i-1}$来更新$G_i$
   $G_i,D_i=argmi{n}_{G}ma{x}_D\{L_{adv}^{f_{i-1}}+\alpha L_{GAN}+\beta L_{hinge}\}$
2. 固定$G_i$来更新$f_i$
   先用$f_{i-1}$来初始化$f_i$；
   然后用$G_i$来生成对抗样本$x+G_i(x)$
   基于新的访问结果来更新$f_i$：$f_i=argmi{n}_f{E}_x[H(f(x),b(x))]+E_x[H(f(x+G_i(x))),b(x+G_i(x))]$ (同时用原图和对抗样本来更新f)

以上是初步理解 欢迎一起来探讨～～～～