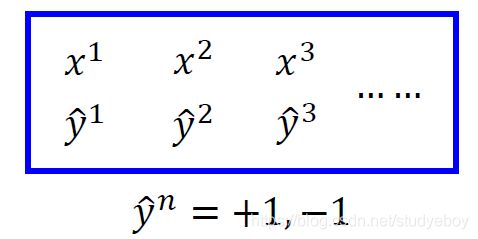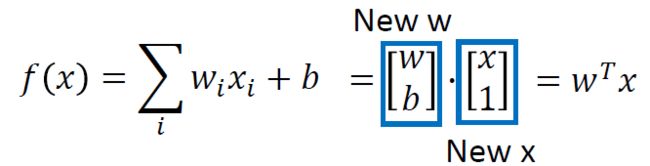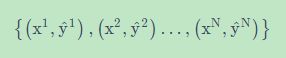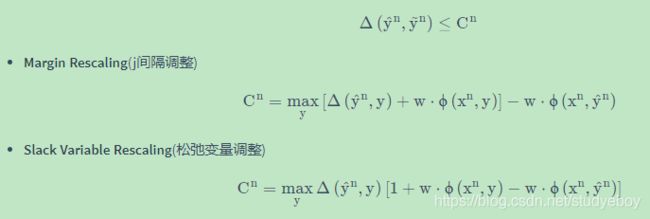李宏毅机器学习—读书笔记
李宏毅机器学习笔记(LeeML-Notes)
leeml-notes
机器学习
人工智慧(Artificial Intelligence)是我们想要达成的目标,希望机器可以跟人一样的聪明。机器学习(Machine Learning)是想要达成目标的手段,希望机器通过学习方式,跟人一样聪明。而深度学习(Deep Learning)是机器学习的其中一种方法。
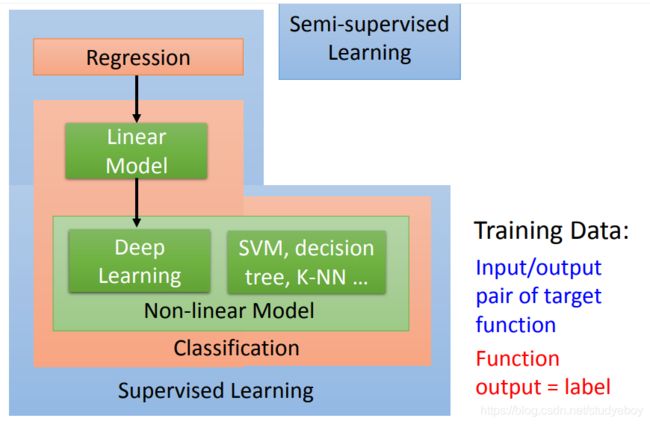
监督学习
Regression和Classification的差别是要机器输出的东西的类型是不一样的。在Regression中机器输出的是一个数值,在Classification里面机器输出的是类别。假设Classification问题分成两种,一种叫作二分类输出的是是或否(Yes or No);另一类叫作多分类(Mulit-class),在Multi-class中是让机器做一个选择题,等于是给他数个选项,每个选项都是一个类别,让它从数个类别里选择正确的类别。
上面说的都是让machine去解的任务,下面在解任务的过程中,第一步就是要选择function set,选不同的function set就是选不同的model。Model有很多中,最简单的就是线性模型,非线性模型中最常见的就是Deep Learning。

在做Deep Learning时,它的function是特别复杂的,所以它可以做特别复杂的事情。比如他可以做影响识别,这个复杂的function可以描述pixel和class之间的关系。

用Deep learning的技术也可以让机器下围棋, 下围棋这个task 其实就是一个分类的问题。对分类问题我们需要一个很复杂的function,输入是一个棋盘的格子,输出就是下一步应该落子的位置。我们知道一个棋盘上有十九乘十九的位置可以落子,所以下围棋这件事情,可以把它想成是一个十九乘十九个类别的分类问题,或者是你可以把它想成是一个有十九乘十九个选项的选择题。

半监督学习
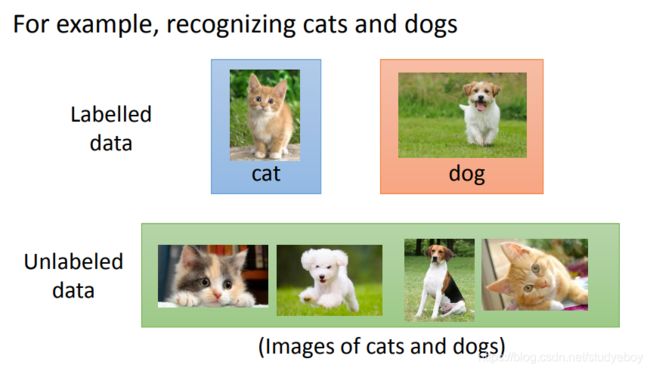
supervised learning(监督学习)的问题是我们需要大量的training data。training data告诉我们要找的function的input和output之间的关系。如果我们在监督学习下进行学习,我们需要告诉机器function的input和output是什么。这个output往往没有办法用很自然的方式取得,需要人工的力量把它标注出来,这些function的output叫做label。
迁移学习
无监督学习
更加进阶的就是无监督学习,我们希望机器可以学到无师自通。如果在完全没有任何label的情况下,到底机器可以学到什么样的事情。



监督学习中的结构化学习
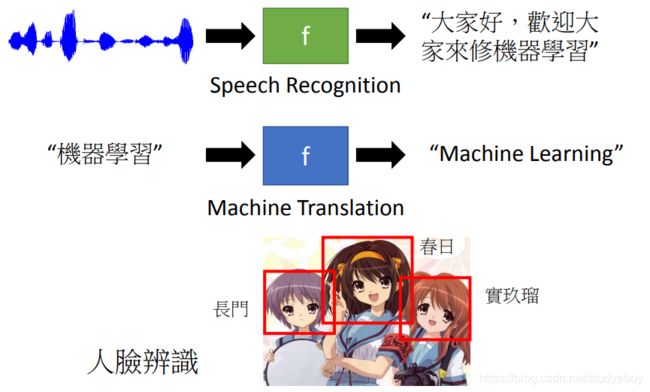
structured learning 中让机器输出的是要有结构性的,举例来说:在语音辨识里面,机器输入是声音讯号,输出是一个句子。句子是要很多词汇拼凑完成。它是一个有结构性的object。或者是说在机器翻译里面你说一句话,你输入中文希望机器翻成英文,它的输出也是有结构性的。或者你今天要做的是人脸辨识,来给机器看张图片,它会知道说最左边是长门,中间是凉宫春日,右边是宝玖瑠。然后机器要把这些东西标出来,这也是一个structure learning问题。
强化学习
在reinforcement learning里面,我们没有告诉机器正确的答案是什么,机器所拥有的只有一个分数,就是他做的好还是不好。机器要在reinforcement learning的情况下学习,机器是非常intelligence的。

监督学习
回归
Regression 就是找到一个函数 functionfunction ,通过输入特征 xx,输出一个数值 ScalarScalar。
- step1:模型假设,选择模型框架(线性模型)
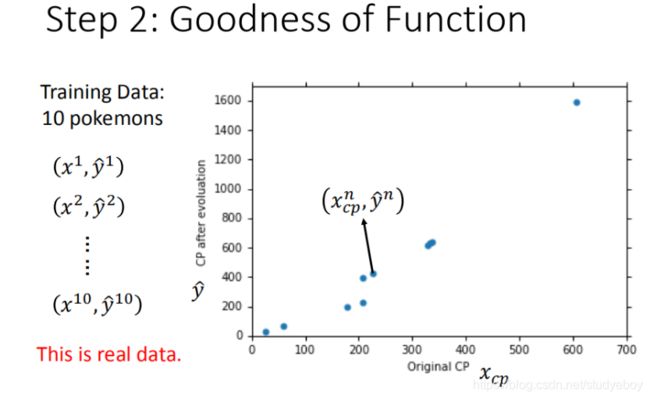
- step2:模型评估,如何判断众多模型的好坏(损失函数)
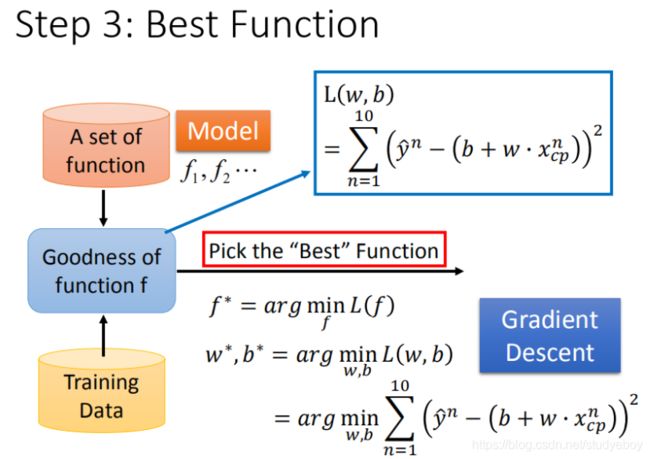
- step3:模型优化,如何筛选最优的模型(梯度下降)
模型假设—线性模型
模型评估—损失函数
最佳模型—梯度下降
- 每一条线围成的圈就是等高线,代表损失函数的值,颜色约深的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向
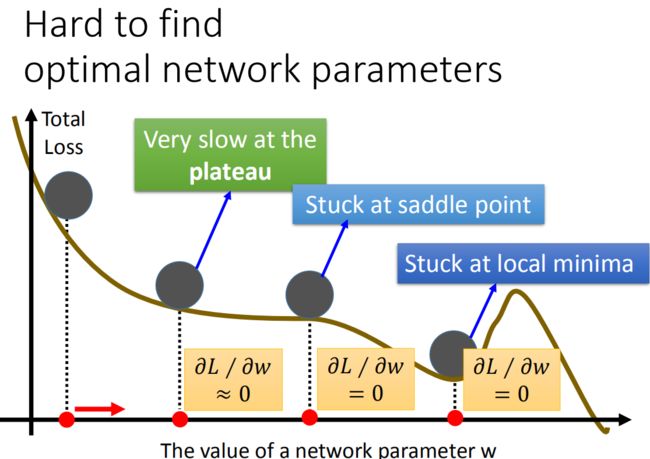
- 梯度下降算法在现实世界中面临的挑战
通过梯度下降gradient descent不断更新损失函数的结果,这个结果会越来越小。其实在线性模型里面都是一个碗的形状(山谷形状),梯度下降基本上都能找到最优点,但是再其他更复杂的模型里面,就会遇到 问题2 和 问题3 了:
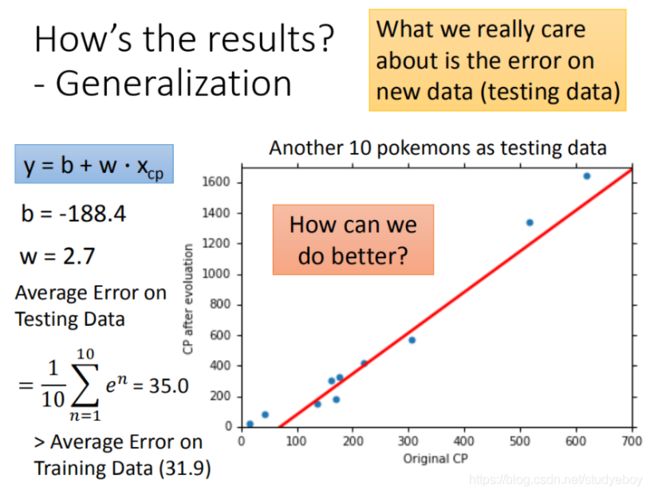
如何验证训练好的模型的好坏
更强大复杂的模型:1元N次线性模型
过拟合问题出现
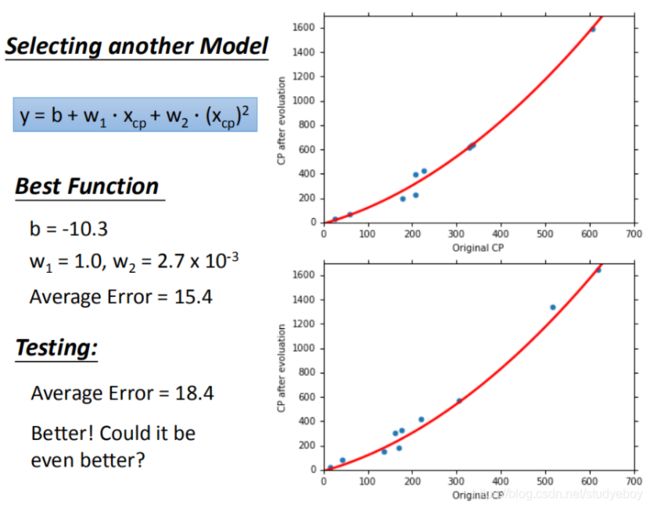
在模型上,我们再可以进一部优化,使用更高次方的模型。

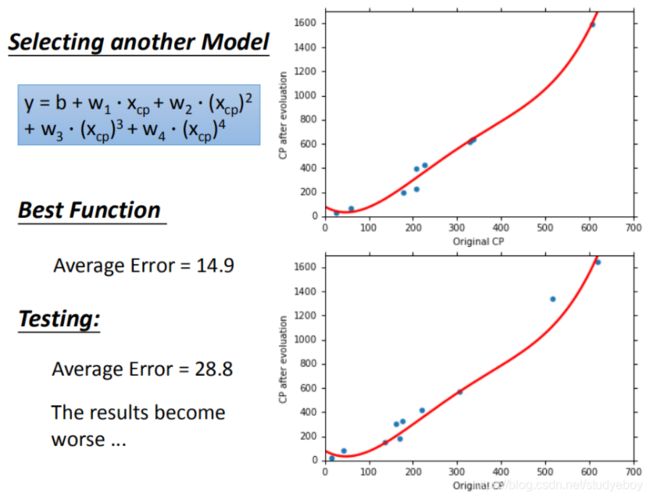

在训练集上面表现更为优秀的模型,为什么在测试集上效果反而变差了?这就是模型在训练集上过拟合的问题。

将错误率结果图形化展示,发现3次方以上的模型,已经出现了过拟合的现象:

优化步骤
- 模型更强大表现更好(更多参数,更多input)
更多特征,更多input,数据量没有明显增加,仍旧导致overfitting。 - 正则化
更多特征,但是权重 ww 可能会使某些特征权值过高,仍旧导致overfitting,所以加入正则化。


误差
Error = Bias + Variance
Error反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
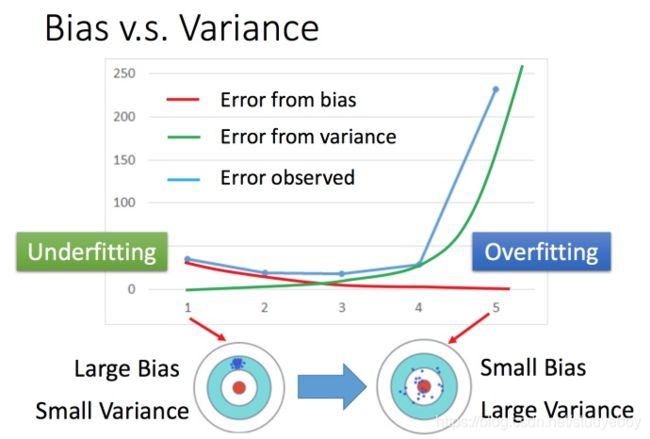
- 偏差大—欠拟合
训练集上表现不好,偏差大—欠拟合,需要重新设计模型。 - 方差大—过拟合
训练集上表现好,测试集上表现不好,方差大—过拟合,需要更多的数据。
在偏差和方差之间就需要一个权衡,选择的模型,可以平衡偏差和方差产生的错误,使得总错误最小。
-
交叉验证
交叉验证 就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后再验证集上比较,确定出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试,此时一般得到的错误都是大一些的。

-
N-折交叉验证
将训练集分成N份,比如分成3份。比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。

梯度下降
调整学习率
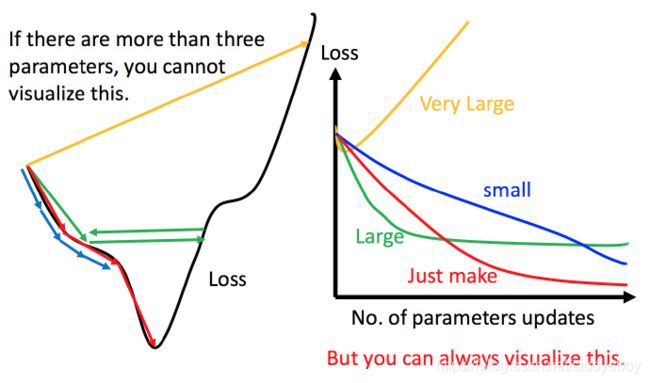
上图左边黑色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
-
自适应学习率
随着次数的增加,通过一些因子来减少学习率。通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率,update好几次参数之后呢,比较靠近最低点了,此时减少学习率
比如 η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1ηt, t t t是次数。随着次数的增加, η t \eta^t ηt 减小。学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
-
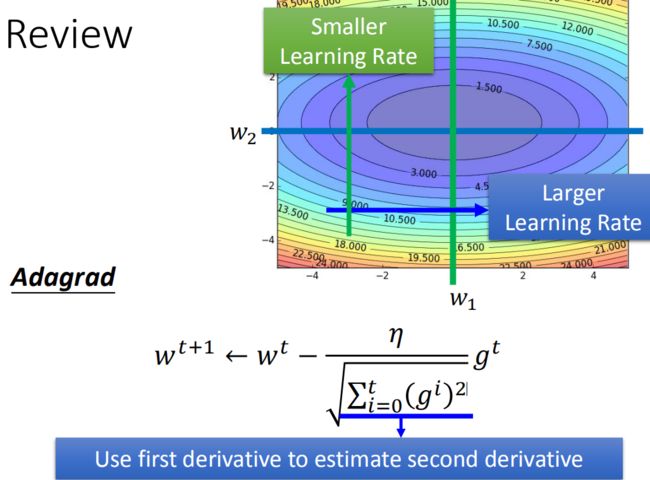
Adagrad算法

参数的更新过程

将 Adagrad 的式子进行化简:

在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。
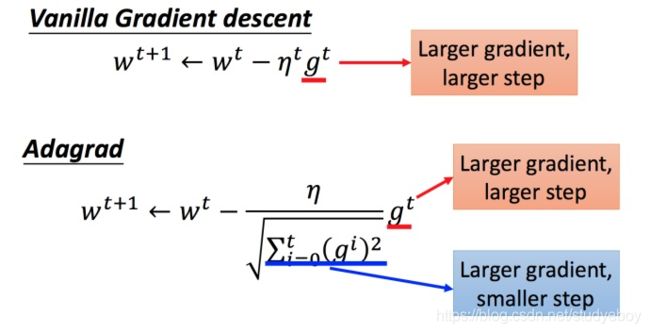
直观的解释:

正式的解释:
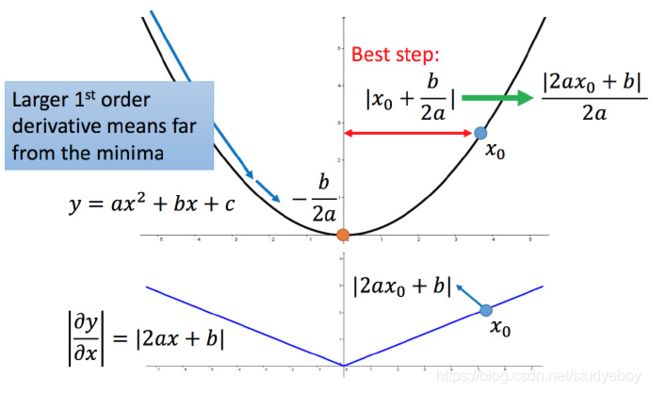
比如初始点在 x 0 x_0 x0,最低点为 − b 2 a −\frac{b}{2a} −2ab,最佳的步伐就是 x 0 x_0 x0 到最低点之间的距离 ∣ x 0 + b 2 a ∣ \left | x_0+\frac{b}{2a} \right | ∣∣x0+2ab∣∣,也可以写成 ∣ 2 a x 0 + b 2 a ∣ \left | \frac{2ax_0+b}{2a} \right | ∣∣2a2ax0+b∣∣。而刚好 ∣ 2 a x 0 + b ∣ |2ax_0+b| ∣2ax0+b∣就是方程绝对值在 x 0 x_0 x0这一点的微分。这样可以认为如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
结论1:梯度越大,就跟最低点的距离越远。
多参数下结论不一定成立
对比不同的参数

上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w 1 w_1 w1,就像图中蓝色的线,得到右边上图结果;如果只考虑参数 w 2 w_2 w2,就像图中绿色的线,得到右边下图的结果。确实对于 a 和 b,结论1是成立的,同理 c 和 d 也成立。但是如果对比a 和 c,就不成立了,c 比 a 大,但 c 距离最低点是比较近的。所以结论1是在没有考虑跨参数对比的情况下,才能成立的。所以还不完善。
之前说到的最佳距离 ∣ 2 a x 0 + b 2 a ∣ \left | \frac{2ax_0+b}{2a} \right | ∣∣2a2ax0+b∣∣,还有个分母 2a 。对function进行二次微分刚好可以得到:
∂ 2 y ∂ x 2 = 2 a (7) \frac{\partial ^2y}{\partial x^2} = 2a \tag7 ∂x2∂2y=2a(7)
所以最好的步伐应该是:
一 次 微 分 二 次 微 分 \frac{一次微分}{二次微分} 二次微分一次微分
即不止和一次微分成正比,还和二次微分成反比。最好的step应该考虑到二次微分:

Adagrad 进一步的解释

对于 ∑ i = 0 t ( g i ) 2 \sqrt{\sum_{i=0}^t(g^i)^2} ∑i=0t(gi)2 就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)。
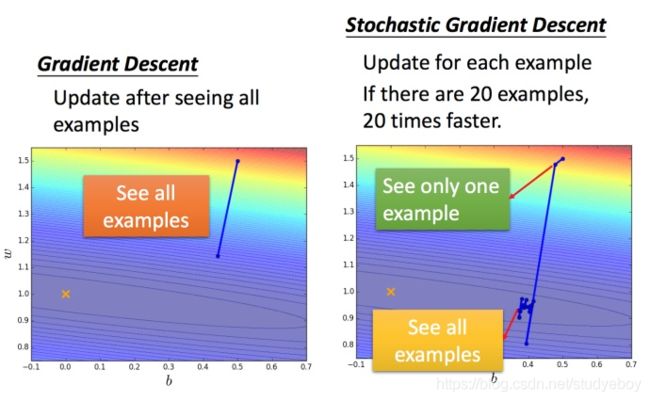
随机梯度下降法
特征收缩
两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。

为什么要特征缩放?

上图左边是 x 1 x_1 x1的scale比 x 2 x_2 x2 要小很多,所以当 w 1 w_1 w1 和 w 2 w_2 w2 做同样的变化时, x 1 x_1 x1 对 y y y 的变化影响是比较小的, x 2 x_2 x2对 y y y 的变化影响是比较大的。
坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 x 1 x_1 x1对 y y y 的变化影响比较小,所以 w 1 w_1 w1对损失函数的影响比较小, w 1 w_1 w1 对损失函数有比较小的微分,所以 w 1 w_1 w1方向上是比较平滑的。同理 x 2 x x_2x x2x对 y y y 的影响比较大,所以 w 2 w_2 w2对损失函数的影响比较大,所以在 w 2 w_2 w2 方向有比较尖的峡谷。
上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
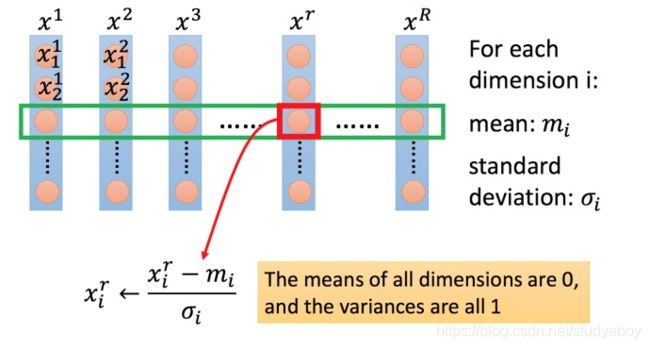
对每一个维度 i i i(绿色框)都计算平均数,记做 m i m_i mi;还要计算标准差,记做 σ i \sigma _i σi。
然后用第 r r r 个例子中的第 i i i 个输入,减掉平均数 m i m_i mi,然后除以标准差 σ i \sigma _i σi,得到的结果是所有的维数都是 0,所有的方差都是 1。
概率分类模型
分类是找一个function函数,输入对象x特征,输出是该对象属于n个类别中是属于哪一个。
概率与分类的关系
假设两个盒子,各装了5个球,随机抽取一个球,抽到的是盒子1的球的概率为2/3,是盒子2的球的概率是1/3。从盒子中蓝色球和绿色求的分配可以得到:
- 在盒子1中随机抽一个球,是蓝色的概率为4/5,蓝色的概率为1/5.
- 在盒子2中随机抽一个球,是蓝色的概率为2/5,绿色的概率为3/5.

求随机从两个盒子中抽取一个球,抽到的是盒子1中蓝色球的概率是多少?
P ( B 1 ∣ B l u e ) = P ( B l u e ∣ B 1 ) P ( B 1 ) P ( B l u e ∣ B 1 ) P ( B 1 ) + P ( B l u e ∣ B 2 ) P ( B 2 ) = 4 5 ∗ 2 3 4 5 ∗ 2 3 + 2 5 ∗ 1 3 = 4 5 \begin{aligned} P(B1|Blue) & =\frac{P(Blue|B_1)P(B_1)}{P(Blue|B_1)P(B_1)+P(Blue|B_2)P(B_2)} \\ & = \frac{\frac{4}{5}* \frac{2}{3}}{\frac{4}{5} * \frac{2}{3} + \frac{2}{5} * \frac{1}{3}} \\ & =\frac{4}{5} \end {aligned} P(B1∣Blue)=P(Blue∣B1)P(B1)+P(Blue∣B2)P(B2)P(Blue∣B1)P(B1)=54∗32+52∗3154∗32=54
所以两个盒子中抽一个球,抽到的是盒子1中蓝色球的概率是 4 5 \frac{4}{5} 54。
先验概率
将两个盒子换成两个类别

那么两个盒子中抽一个球,抽到的是盒子1中篮球的概率是多少?相当于两个类别中抽一个x,抽到的是类别1中x的概率是多少?可以转化成,随机给一个x,那么它属于哪一个类别(属于概率相对比较大的类别)?
高斯分布

可以把高斯分布当作一个function,输入就是一个向量x,输出就是选中x的概率,实际上高斯分布不等于概率,只是和概率成正比,这里简单说成概率。function由期望 μ \mu μ和协方差矩阵 Σ \Sigma Σ决定。同样的 Σ \Sigma Σ,不同的 μ \mu μ,概率分布的最高点的位置是不同的。同样的 μ \mu μ,不同的 Σ \Sigma Σ,概率分布的最高点是一样的,但是离散度是不一样的。
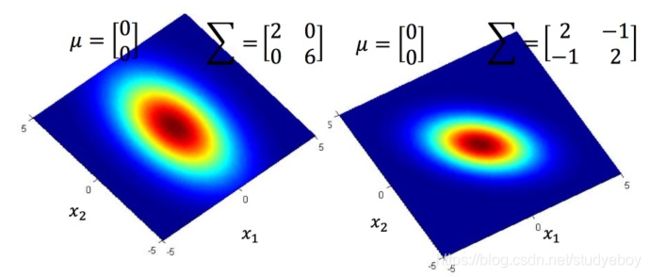
假设这些特征点是从高斯分布(Gaussian distribution)中采样的,需要从这些特征点找出符合的那个高斯分布。假设通过这些特征点估测出了 μ \mu μ和协方差矩阵 Σ \Sigma Σ。期望是图中黄色点,协方差矩阵是红色的范围。给定一个新点,用估测出的期望和协方差矩阵写出高斯分布的 f u n c t i o n f μ , Σ ( x ) functionf_{\mu, \Sigma}(x) functionfμ,Σ(x),然后将 x x x带进去,计算出被挑选出来的概率。

最大似然估计
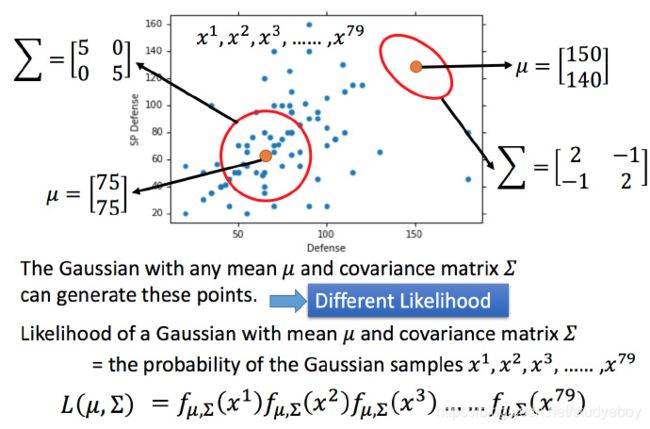
对于这些点,任意期望和协方差矩阵构成的高斯分布,都可以生成这些点。当然,图像汇总左边的高斯分布生成这些点,比右边高斯分布生成这些点的几率要大。给定一个 μ \mu μ和 Σ \Sigma Σ,它生成这79个点的概率为图中的 L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ), L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ)称为样本的似然函数。将使得 L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ)最大的 L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ),记作 L ( μ ∗ , Σ ∗ ) L(\mu^*, \Sigma ^*) L(μ∗,Σ∗), L ( μ ∗ , Σ ∗ ) L(\mu^*, \Sigma ^*) L(μ∗,Σ∗)就是所有 L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ)的Maximum Likelihood(最大似然估计)。

这些解法很直接,直接对 L ( μ , Σ ) L(\mu, \Sigma) L(μ,Σ)求两个偏微分,求偏微分是0的点。
应用最大似然估计计算期望和协方差
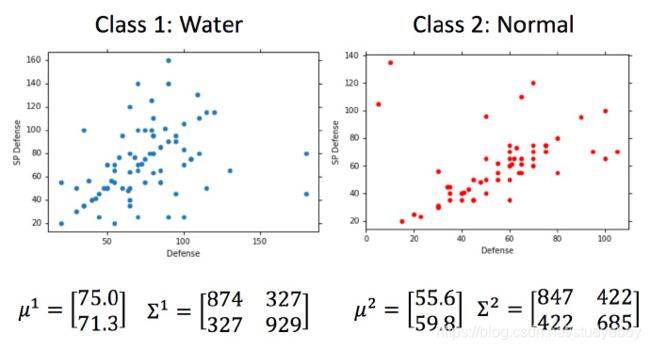
算出某属性高斯分布的期望和协方差矩阵的最大似然估计值。
模型优化
通常不会给每个高斯分布计算出一套不同的最大似然估计,协方差矩阵是和输入feature大小的平方成正比,所以当feature很大的时候,协方差矩阵是可以增长很快的。考虑到model参数过多,容易overfitting,为了有效减少参数,给描述这两个类别的高斯分布相同的协方差矩阵。

修改似然函数为 L ( μ 1 , μ 2 , Σ ) L(\mu_1, \mu_2, \Sigma) L(μ1,μ2,Σ), μ 1 \mu_1 μ1, μ 2 \mu_2 μ2的计算方法相同,分别加起来平均即可; Σ \Sigma Σ的计算方法不同。

概率模型-建模三部曲

实际做的就是找一个概率分布模型,可以最大化产生data的likelihood。
为什么是概率分布,常见的假设:

假设每一个维度用概率分布模型产生出来的几率是相互独立的,所以可以将 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)拆解。可以认为每个 P ( x k ∣ C 1 ) P(x_k|C_1) P(xk∣C1)产生的概率都符合一维的高斯分布,即此时 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)的高斯分布的协方差是对角型的(不是对角线的地方值都是0),这样可以减少参数的量。
对于二元分类来说,通常不会用高斯分布,假设是符合Bernoulli distribution(伯努利分布)。
假设所有的feature都是相互独立产生的,这种分类叫作Naive Bayes Classifier(朴素贝叶斯分类器)。
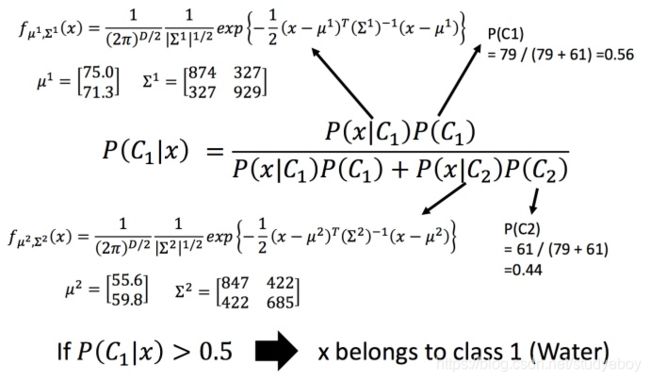
后验概率
将 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)整理,得到一个 σ ( z ) \sigma(z) σ(z),这叫做Sigmoid function。

数学推导:



求得 z z z,然后:

化简 z z z, x x x的系数记作向量 w T w^T wT,后面3项都是标量,所以三个数字加起来记作 b b b。最后 P ( C 1 ∣ x ) = σ ( w ⋅ x + b ) P(C_1|x)=\sigma(w \cdot x + b) P(C1∣x)=σ(w⋅x+b)。从这个式子可以看出当共用协方差矩阵的时候,分界线是线性的。
估测 N 1 , N 2 , μ 1 , μ 2 , Σ N_1, N_2, \mu_1, \mu_2, \Sigma N1,N2,μ1,μ2,Σ,就可以直接得到结果了。
logistic回归
逻辑回归的函数集
分类问题的解决方法是推导出函数集的形式为:

将函数集可视化

这个函数集的分类问题叫作Logistic Regression(逻辑回归),逻辑回归和线性回归函数集的比较:

定义损失函数
有一个训练集,每个对象分别对应属于哪个类型,例如 x 3 x^3 x3属于 C 2 C_2 C2。假设这些数据都是由后验概率 f w , b ( x ) = P w , b ( C 1 ∣ x ) f_{w,b}(x)=P_{w,b}(C1|x) fw,b(x)=Pw,b(C1∣x)产生的。
给定一组 w w w和 b b b,可以计算这组 w , b w,b w,b下产生图中N个训练数据的概率,
L ( w , b ) = f w , b ( x 1 ) f w , b ( x 2 ) ( 1 − f w , b ( x 3 ) ) . . . f w , b ( x N ) L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))...f_{w,b}(x^N) L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))...fw,b(xN)
对于使得 L ( w , b ) L(w,b) L(w,b)最大的 w w w和 b b b,记作 w ∗ w^* w∗和 b ∗ b^* b∗,即
w ∗ , b ∗ = a r g m a x w , b L ( w , b ) w^*,b^*=argmax_{w,b}L(w,b) w∗,b∗=argmaxw,bL(w,b)

将训练集数字化,并且将求max通过取负自然对数转化为求min:

然后将 − l n L ( w , b ) -lnL(w,b) −lnL(w,b)改写为下图中带蓝色下划线式子的样子:

图中蓝色下划线实际上代表的是两个伯努利分布(0-1分布,两点分布)的cross entropy(交叉熵)。
假设有两个分布p和q,如图中蓝色方框所示,这两个分布之间交叉熵的计算方式就是H(p,q);交叉熵代表的含义是这两个分布有多接近,如果两个分布是一模一样的,那么计算出的交叉熵就是熵。
逻辑回归和线性回归,损失函数比较:

直观理解,如果把function的输出和target都看作是两个伯努利分布,所做的事情就是希望这两个分布越接近越好。
寻找最好的函数
用梯度下降法求解
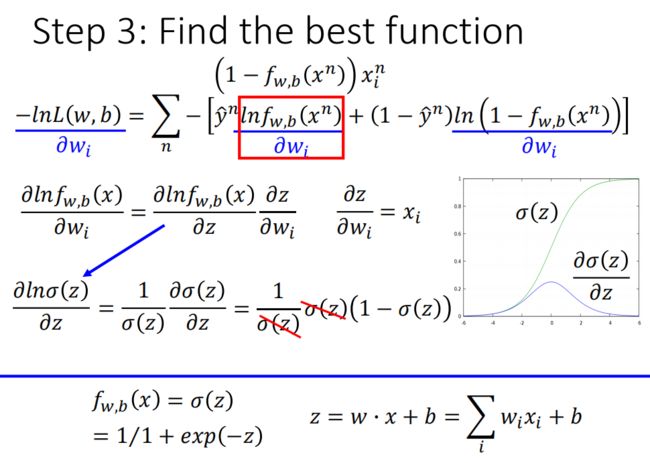


逻辑回归和线性回归比较,挑选最好的function

对于逻辑回归,target y n y^n yn是0或1,输出是介于0和1之间。而线性回归的target可以是任何实数,输出也可以是任何值。
逻辑回归用平方误差
考虑逻辑回归用平方误差形式,在step3计算出了对 w i w_i wi的偏微分。假设 y n = 1 y^n=1 yn=1,如果 f w , b ( x n ) = 1 f_{w,b}(x_n)=1 fw,b(xn)=1,就非常接近target,会导致偏微分中第一部分为0,从而偏微分为0;而 f w , b ( x n ) = 0 f_{w,b}(x_n)=0 fw,b(xn)=0,会导致第二部分为0,从而偏微分也是0.

对比两个参数的变化,对总的损失函数作图:

如果是交叉熵,距离target越远,微分值就越大,就可以做到距离target越远,更新参数越快。而平方误差在距离target很远的时候,微分值非常小,会造成移动的速度非常慢,这就是很差的效果了。
判别模型和生成模型
逻辑回归的方法称为Discriminator(判别)方法,用高斯来描述后验概率,称为Generative(生成)方法。它们的函数集都是一样的。

如果是逻辑回归,可以直接用梯度下降法找出 w w w和 b b b;如果是概率生成模型,例如用高斯来描述后验概率,需要求出 μ 1 , μ 2 \mu^1, \mu^2 μ1,μ2,协方差矩阵的逆,然后就能算出 w w w和 b b b。
用逻辑回归和概率生成模型找出来的 w w w和 b b b是不一样的。

图中画的是只考虑两个因素,如果考虑所有因素,结果是逻辑回归的效果好一些。
下图的训练集有13组数据,类别1里面两个特征都是1,剩下的(1, 0), (0, 1), (0, 0) 都认为是类别2;然后给一个测试数据(1, 1),它是哪个类别呢?人类来判断的话,不出意外基本都认为是类别1。下面看一下朴素贝叶斯分类器(Naive Bayes)会有什么样的结果。

朴素贝叶斯分类器如图中公式: x x x属于 C i C_i Ci 的概率等于每个特征属于 C i C_i Ci 概率的乘积。

计算出 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)的结果是小于0.5的,即对于朴素贝叶斯分类器来说,测试数据 (1, 1)是属于类别2的,这和直观上的判断是相反的。其实这是合理,实际上训练集的数据量太小,但是对于 (1, 1)可能属于类别2这件事情,朴素贝叶斯分类器是有假设这种情况存在的。所以结果和人类直观判断的结果不太一样。
生成方法的优势:
训练集数量很小的情况,因为判别方法没有做任何假设,就是看着训练集来计算,训练解数量越来越大的时候,error会越小。而生成方法会自己脑补,受到数据量的影响比较小。
多类别分类
-
softmax
假设有3个类别,每个都有自己的weight和bias。

把 z 1 , z 2 , z 3 z_1,z_2,z_3 z1,z2,z3放到一个叫做Softmax的方程中,Softmax做的事情就是它们进行exponential(指数化),将exponential 的结果相加,再分别用 exponential 的结果除以相加的结果。原本 z 1 , z 2 , z 3 z_1,z_2,z_3 z1,z2,z3 可以是任何值,但做完Softmax之后输出会被限制住,都介于0到1之间,并且和是1。Softmax做事情就是对最大值进行强化。输入x,属于类别1的几率是0.88,属于类别2的几率是0.12,属于类别3的几率是0。
Softmax的输出就是用来估计后验概率(Posterior Probability)。
-
softmax的输出可以用来估计后验概率
假设有3个类别,这3个类别都是高斯分布,他们也共用同一个协方差矩阵,进行推导可以得到Softmax。用信息论学科中的Maximum Entropy(最大熵)也可以推导出softmax。指数簇分布的最大熵等价于其指数形式的最大似然界。二项式的最大熵解等价于二项式指数形式(sigmoid)的最大似然,多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然。假设分布求解最大熵,引入拉格朗日函数,求偏导数等于0,直接求出就是sigmoid函数形式。还有很多指数簇分布都有对应的最大似然界。而且,单个指数簇分布往往表达能力有限,就引入了多个指数簇分布的混合模型,比如高斯混合,引出了EM算法。想LDA就是多项式分布的混合模型。
逻辑回归的限制

两个类别分布在两个对角线两端,用逻辑回归不能处理,因为逻辑回归所能做的分界线就是一条直线,没办法将红蓝色用一条直线分开。

- 特征转换
特征转换的方式很多,举例类别1转化为某个点到 (0,0)点的距离,类别2转化为某个点到 (1,1) 点的距离。然后问题就转化右图,此时就可以处理了。但是实际中并不是总能轻易的找到好的特征转换的方法。

- 级联逻辑回归模型
可以将很多的逻辑回归接到一起,就可以进行特征转换。比如上图就用两个逻辑回归 对 z 1 , z 2 z_1,z_2 z1,z2来进行特征转换,然后对于 x 1 ′ , x 2 ′ x_1^{'},x_2^{'} x1′,x2′,再用一个逻辑回归 z z z来进行分类。
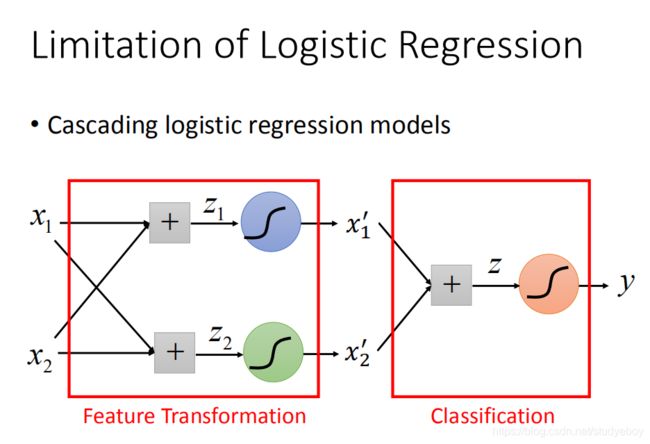
对上述例子用这种方式处理:

右上角的图,可以调整参数使得得出这四种情况。同理右下角也是
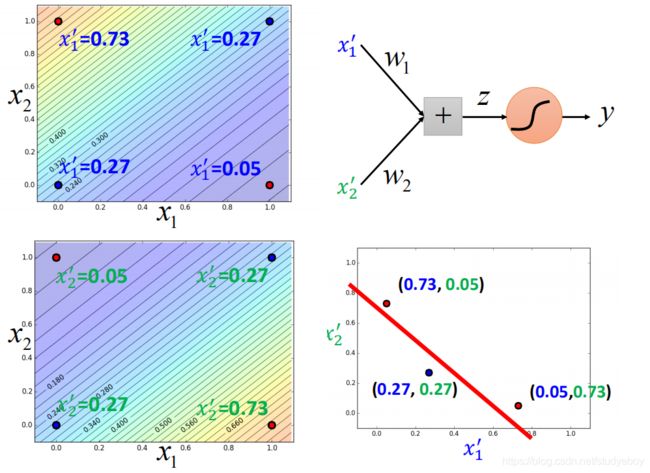
经过这样的转换之后,点就被处理为可以进行分类的结果。

一个逻辑回归的输入可以来源于其他逻辑回归的输出,这个逻辑回归的输出也可以是其他逻辑回归的输入。把每个逻辑回归称为一个 Neuron(神经元),把这些神经元连接起来的网络,就叫做 Neural Network(神经网络)。
深度学习简介
神经网络
-
完全连接前馈神经网络
前馈(feedforward)也可以称为前向,从信号流向来理解就是输入信号进入网络后,信号流动是单向的,即信号从前一层流向后一层,一直到输出层,其中任意两层之间的连接并没有反馈(feedback),亦即信号没有从后一层又返回到前一层。

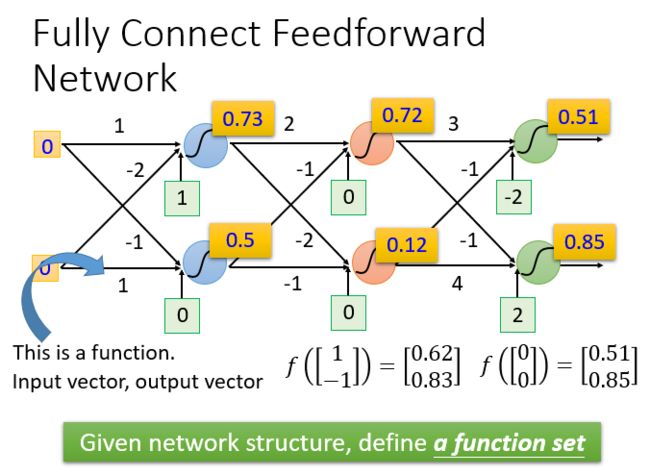
不论是回归模型(linear model)还是逻辑回归(logistic regression)都是定义了一个函数集(function set)。可以给神经网络结构的参数设置不同的数,就是不同的函数(function)。这些可能的函数(function)结合起来就是一个函数集(function set)。这个时候的函数集(function set)是比较大的,是以前的回归模型(linear model)等没有办法包含的函数(function),所以说深度学习能够表达出以前所不能表达的情况。
-
全连接和前馈的理解
- 全连接:因为layer1 与 layer2之间两两都有连接,所以叫作Fully Connect。
- 前馈:因为现在的传递的方向是由后往前传,所以叫作Feedforward。

-
深度的理解
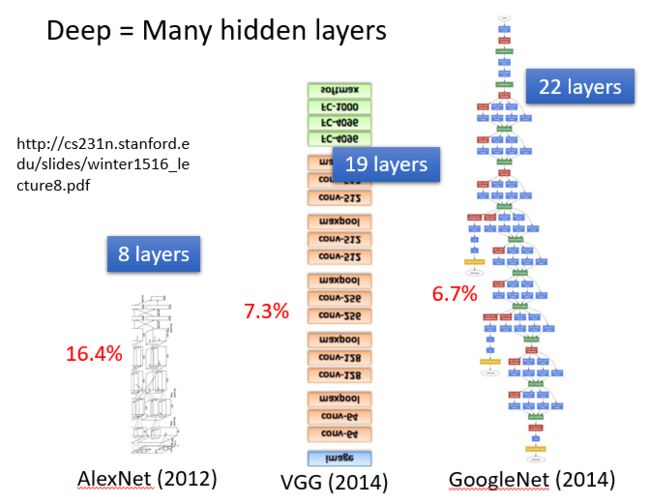

- 矩阵计算
随着层数变多,错误率降低,随之运算量增大,通常的都是超亿万级的计算。引入矩阵计算能使得运算的速度及效率高很多。


-
本质:通过隐藏层进行特征转换
把隐藏层通过特征提取来替代原来的特征工程,在最后一个隐藏层输出的就是一组新的特征,而对于输出层,其实是把前面的隐藏层的输出当作输入,经过特征提取得到一组最好的特征,然后通过一个多分类器得到最后的输出。

-
手写数字识别
输入:一个16x16=256维的向量,每个pixel对应一个dimension,有颜色用1表示,没有颜色用0表示,输出:10个维度,每个维度代表一个数字的置信度。

在这个问题中,唯一需要的就是一个函数,输入是256维的向量,输出是10维的向量,所需要求的就是神经网络函数。
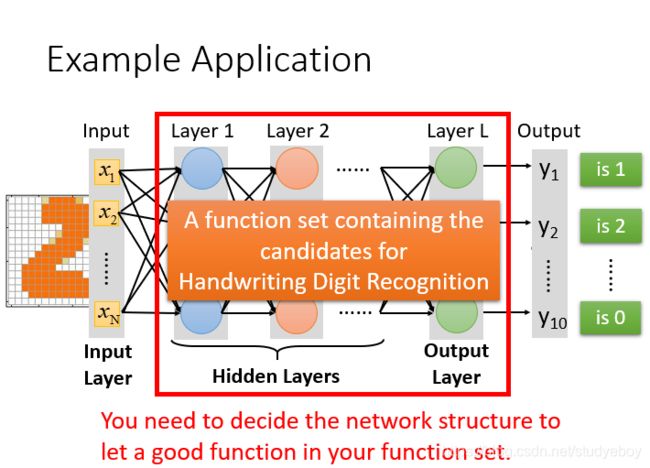
从图中看出神经网络的结构决定了函数集(function set),所以说网络结构(network structured)很关键。

模型评估
对于模型的评估,一般采用损失函数来反应模型的好差,所以对于神经网络来说,采用交叉熵函数来计算,调整参数,让交叉熵越小越好。

要计算所有训练数据的损失,需要把所有的训练数据的损失都加起来,得到一个总体损失。然后在function set里面找到一组函数能最小化这个总体损失,或者找一组神经网络的参数,来最小化总体损失。
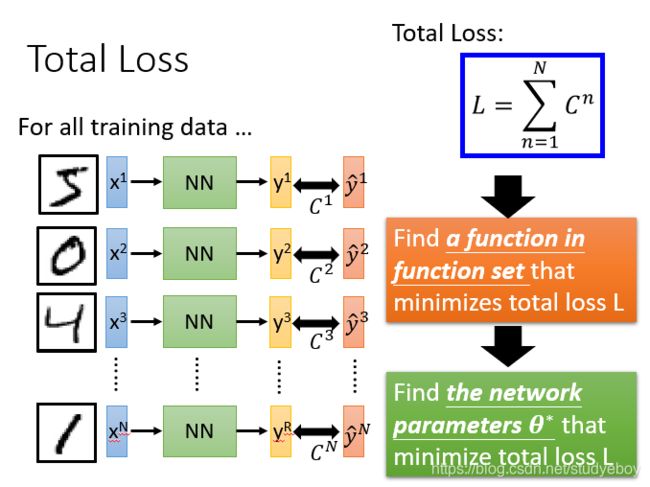
选择最优函数
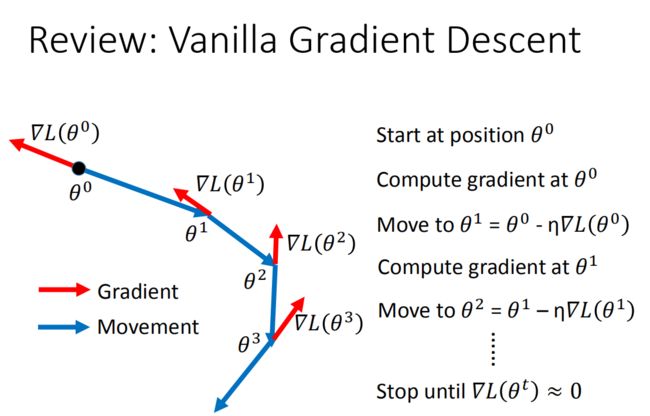
θ \theta θ是一组包含权重和偏差的参数集合,随机找一个初始值,接下来计算一下每个参数对应偏微分,得到的一个偏微分的集合 ∇ L \nabla{L} ∇L就是梯度,有了这些偏微分,我们就可以不断更新梯度得到新的参数,这样不断反复进行,就能得到一组最好的参数使得损失函数的值最小。

在神经网络中计算损失最好的方法就是反向传播,我们可以用很多框架来进行计算损失。

反向传播
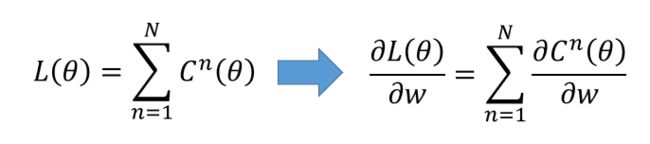



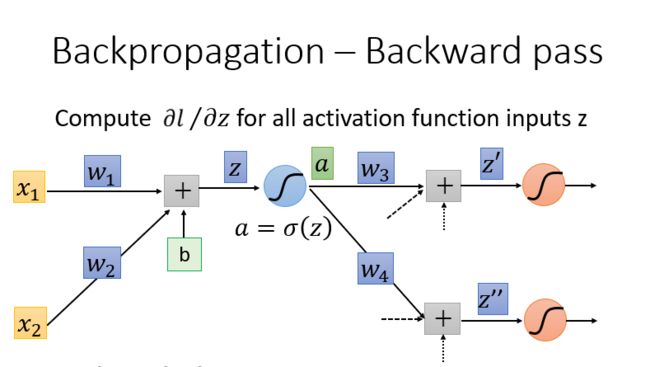

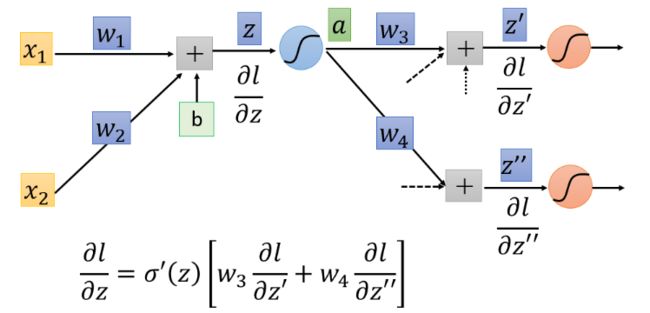


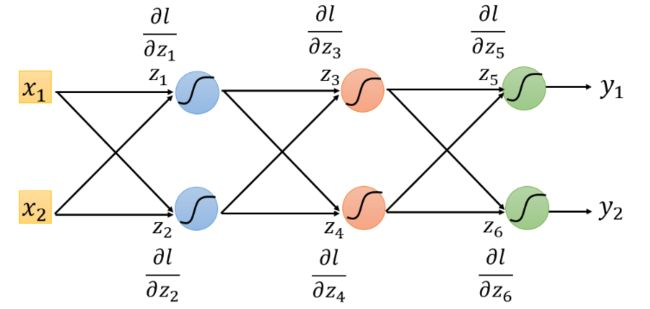

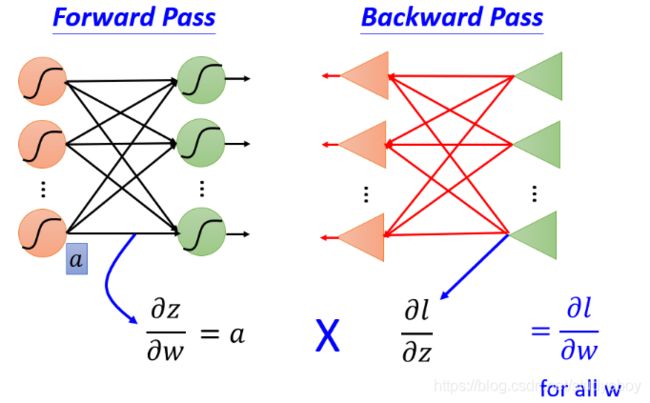
我们的目标是要求计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z(Forward pass的部分)和计算 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l( Backward pass的部分 ),然后把 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z 和 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l 相乘,我们就可以得到 ∂ l ∂ w \frac{\partial l}{\partial w} ∂w∂l,所有我们就可以得到神经网络中所有的参数,然后用梯度下降就可以不断更新,得到损失最小的函数。
深度学习示例
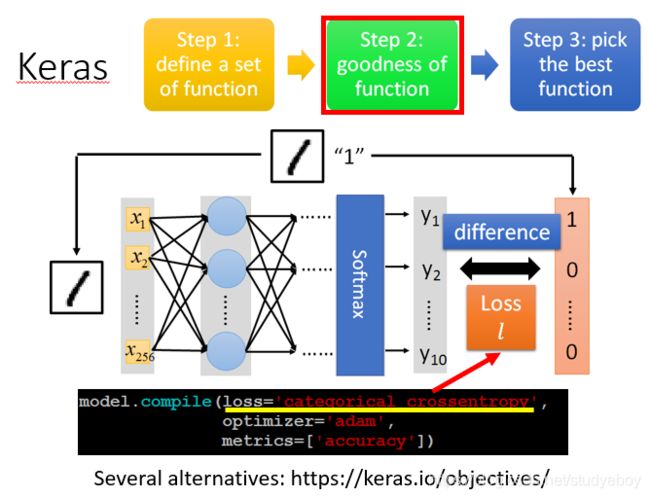
Keras 是一个用 Python 编写的高级神经网络 API,它能够以 TensorFlow, CNTK, 或者 Theano 作为后端运行。
定义模型
模型评估
最佳模型
mini-batch
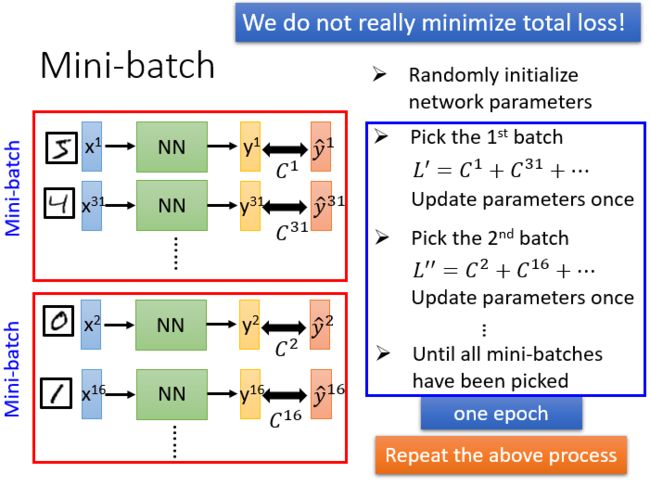



模型的保存和使用
深度学习技巧
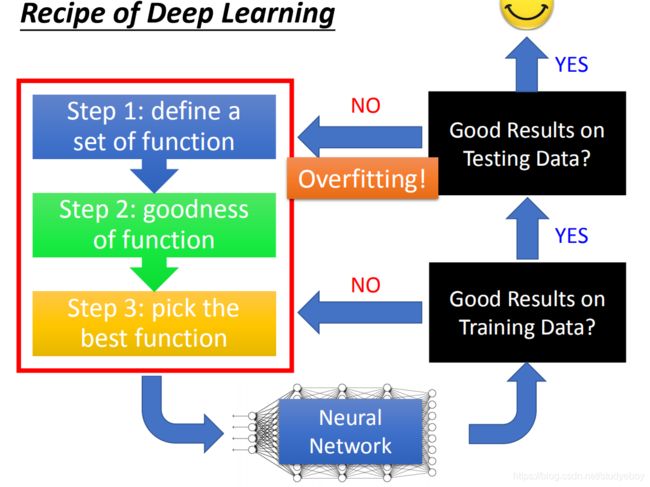
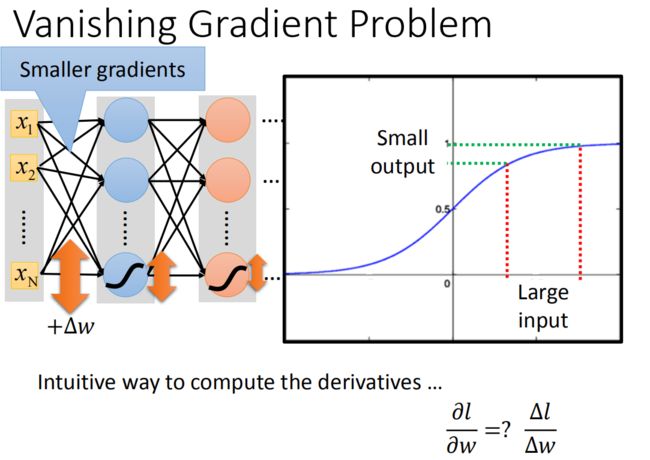
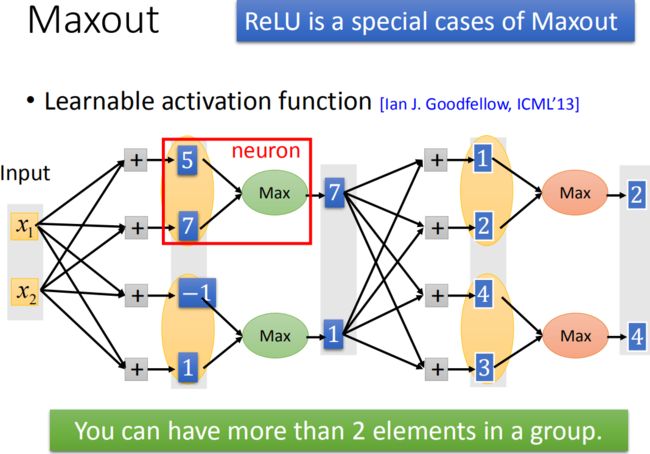
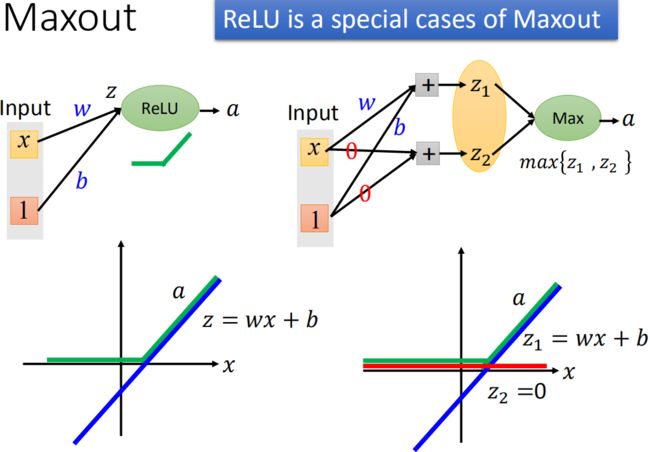
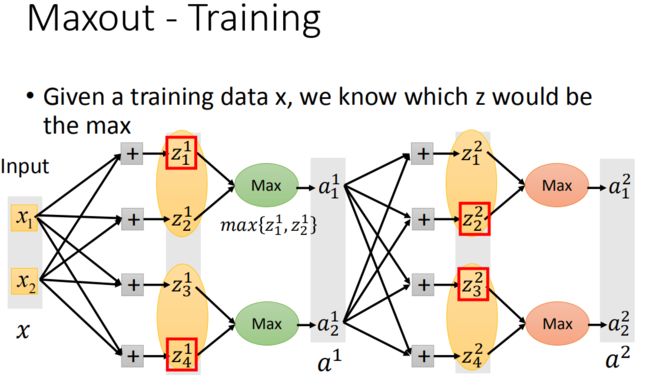
神经网络的表现
改进神经网络




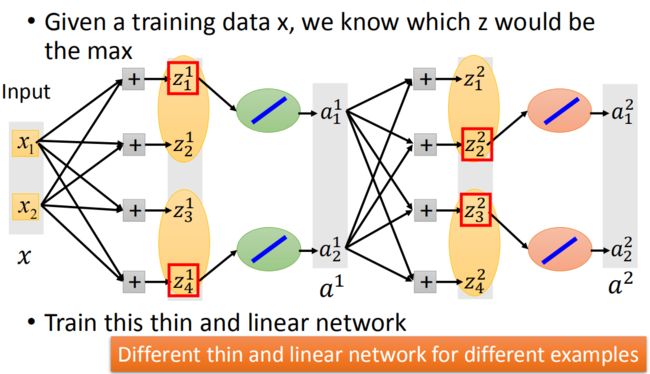
- Adaptive Learning Rate


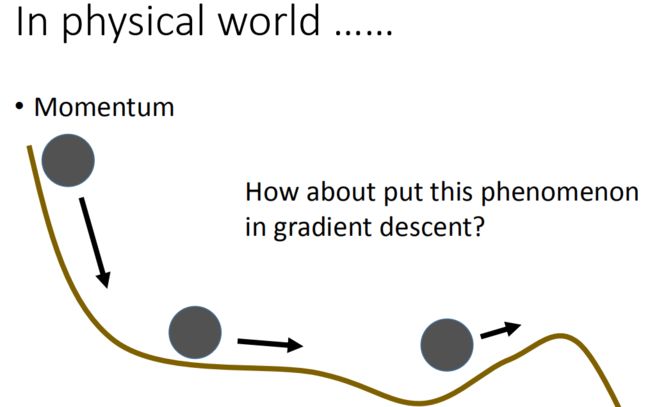






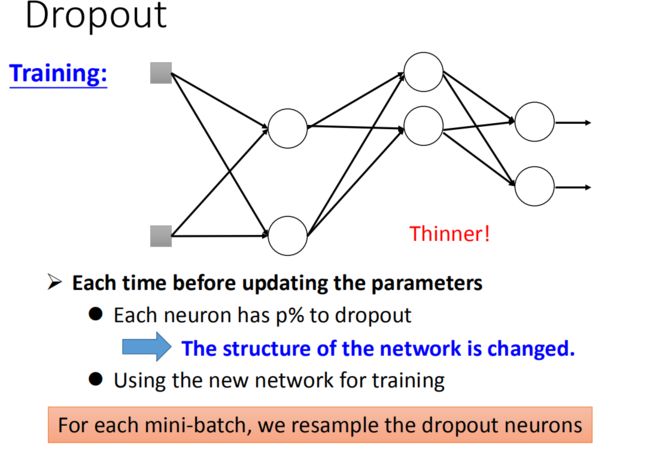
- Dropout


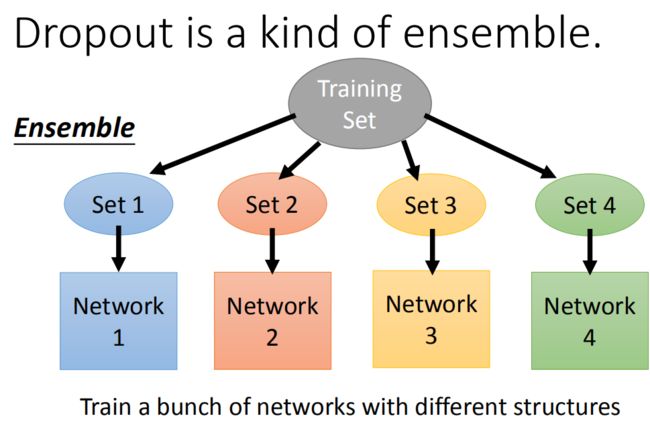




卷积神经网络
为什么用CNN
用一般的neural network来做影像处理,training一个neural network,input一张图片,该不同表示成pixel,即很长的vector。output就是dimension(假如有1000个类别,output就是1000个dimension)。

但是,在training neural network时,在network的structure里面,每一个neural就是代表了一个最基本的classifier。例如:第一层的neural是最简单的classifier,detain有没有绿色出现,有没有黄色出现,有没有斜的条纹。第二个layer是做比这个更复杂的东西,根据第一个layer的output,它看到直线横线就是窗框的一部分,看到棕色纹就是木纹,看到斜条纹+灰色可能是很多的东西(轮胎的一部分等等)。再根据第二个hidden layer的output,第三个hidden layer会做更加复杂的事情。

但是当一直用fully connect feedforward network来做影像处理的时候,会需要太多的参数。例如一张 100 × 100 100\times100 100×100的彩色图像,拉成一个vector,有 100 × 100 × 3 100\times100\times3 100×100×3个pixel,即30000维,如果input vector是30000 dimension。假设hidden layer是1000个neural,那么这个hidden layer的参数就是有 30000 × 1000 30000\times1000 30000×1000,这样参数太多了。CNN就是简化neural network的架构。根据人的知识,某些weight用不上,在开始的时候就把它过滤掉。不用fully connect feedforward network,用比较少的参数来做影像处理。所以CNN比一般的DNN还要简单,用powerknowledge去把原来fully connect layer中一些参数拿掉就成CNN。
-
small region
在影像处理里面,第一层的hidden layer中的neural要做的事就是侦测某一种pattern,有没有一种pattern出现。大部分的pattern其实要比整张的image还要小,对一个neural来说,假设它要知道一个image里面有没有一个pattern出现,不需要看整张image,只要看image的一小部分。假设有一张图片,第一个hidden layer的某一种neural的工作就是要侦测有没有鸟嘴的存在(有一些neural侦测有没有爪子的存在,有没有一些neural侦测有没有翅膀的存在,有么有尾巴的存在,合起来就可以侦测图片中某一只鸟)。假设有一个neural的工作是要侦测有没有鸟嘴的存在,并不需要看整张图,只需要给neural看一笑红色方块的区域(鸟嘴),就可以知道它不是一个鸟嘴。对人来说也是一样,看这一小块区域这是鸟嘴,不需要去看整张图才知道这件事情。所以,每一个neural连接到每一个小块的区域就好了,不需要连接到整张完整的图。

-
same pattern
同样的pattern在image里面,可能会出现在image不同的部分,但是代表的是同样的含义,它们有同样的形状,可以用同样的pattern,同样的参数就可以把pattern侦测出来。比如:这张图里有一张在左上角的鸟嘴,有一张在中央的鸟嘴,但是不需要去训练两个不同的detector,一个专门去侦测左上角的鸟嘴,一个去侦测中央有没有鸟嘴,这样太冗余了。这个neural侦测左上角的鸟嘴跟侦测中央有没有鸟嘴做的事情是一样的。并不需要两个neural去做两组参数,只要这两个neural用同一组参数就可以减少需要的参数量。

-
subsampling
把图像变成原来的十分之一,并不会影响人对这张image的理解,所以把image变小,可以减少需要的参数量。

CNN架构
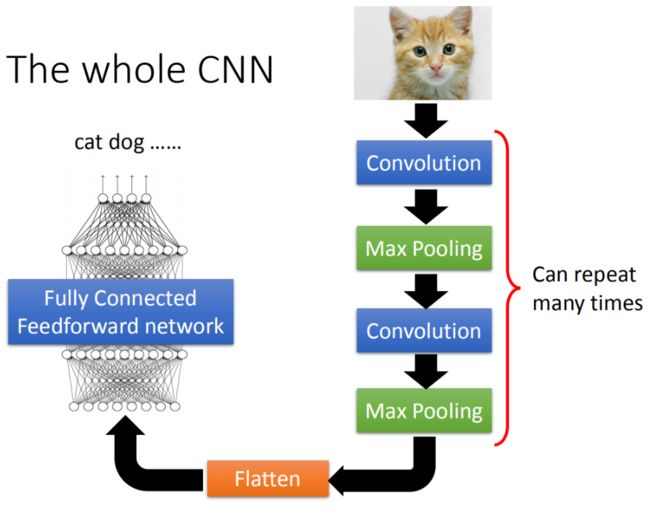
CNN的架构是这样的,首先input一张image后,这张image会通过convolution layer,然后max pooling,然后在做convolution,再做max pooling。这个process可以反复重复无数次,决定完要做的convolution和max pooling之后,再做flatten,把flatten的output丢到一般fully connected feedforward network,然后得到影像辨识的结果。

Convolution
假设network的input是一张 6 × 6 6\times 6 6×6的image,如果是黑白的,一个pixel只需要用一个value去描述它,1就代表有涂墨水,0就代表没有涂到墨水。在convolution layer里面,它由一组的filter,其中每一个filter其实就等同于是fully connect layer里面的一个neuron,每一个filter其实就是一个matrix( 3 × 3 3\times3 3×3),每个filter里面的参数(matrix里面每一个element值)就是network的parameter,该parameter是要学习出来的,并不是需要人去设计的。每个filter如果是 3 × 3 3\times3 3×3的detects意味着它就是再侦测一个 3 × 3 3\times3 3×3的pattern。在侦测pattern的时候不会看整张image,只看 3 × 3 3\times3 3×3的范围内就可以决定有没有某一个pattern的出现。

首先第一个filter是一个 3 × 3 3\times3 3×3的matrix,把这个filter放在image的左上角,把filter的9个值和image的9个值做内积,两边都是1,1,1(斜对角),内积的结果就得到3.移动的距离叫作stride,需要提前人为设置。

你把filter往右移动一格得到-1,再往右移一格得到-3,再往右移动一格得到-1。接下里往下移动一格,得到-3。以此类推(每次都移动一格),直到你把filter移到右下角的时候,得到-1(得到的值如图所示)。 6 × 6 6\times 6 6×6的matrix,经过convolution process就得到 4 × 4 4\times4 4×4的matrix。filter的斜对角的值是1,1,1。所以它的工作就是detain1有没有1,1,1连续左上到右下的出现在这个image里面。同一个pattern出现在了左上角的位置跟左下角的位置,就可以用filter1侦测出来,并不需要不同的filter来做这件事。

在一个convolution layer里面会有很多的filter,另外的filter会有不同的参数,它也做跟filter1一模一样的事情,在filter放到左上角再内积得到结果-1,依次类推。把filter2跟input image做完convolution之后,就得到了另一个 4 × 4 4\times 4 4×4的matrix,红色 4 × 4 4\times 4 4×4跟蓝色的matrix合起来就叫作feature map,几个filter就得到几个image。
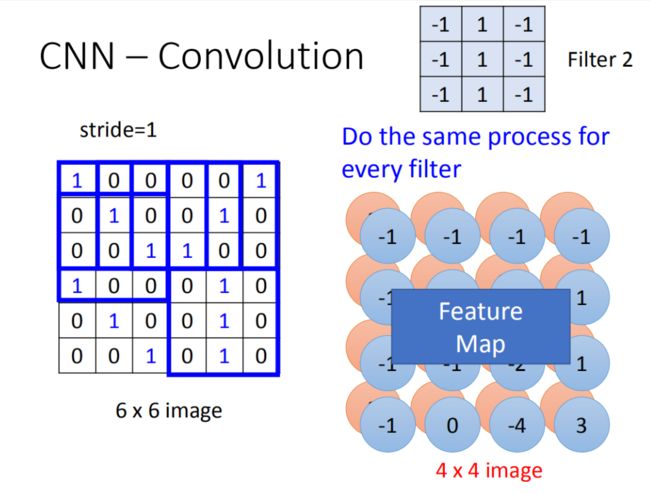
对于一张黑白的image,input是一个matrix,如果是彩色的image,彩色的image由RGB组成,一个彩色的image就是好几个matrix叠在一起就是一个立方体。这时候filter不是一个matrix,filter是一个立方体。如果input是 3 × 6 × 6 3\times6\times6 3×6×6,那filter就是 3 × 3 × 3 3\times3\times3 3×3×3。

convolution和fully connected之间的关系
convolution就是fully connected layer把一些weight拿掉了。

做convolution的时候,我们filter1放到左上角(先考虑filter1),然后做inner product,得到内积为3,这件事情就等同于把6* 6的image拉直(变成如图所示)。然后你有一个neural的output是3,这个neural的output考虑了9个pixel,这9个pixel分别就是编号(1,2,3,7,8,9,13,14,15)的pixel。这个filter做inner product以后的output 3就是某个neuron output 3时,就代表这个neuron的weight只连接到(1,2,3,7,8,9,13,14,15)。这9个weight就是filter matrix里面的9个weight(同样的颜色)。

在fully connected中,一个neural应该是连接在所有的input(有36个pixel当做input,这个neuron应连接在36个input上),但是现在只连接了9个input(detain一个pattern,不需要看整张image,看9个input就好),这样做就是用了比较少的参数了。
将stride=1(移动一格)做内积得到另外一个值-1,假设这个-1是另外一个neural的output,这个neural连接到input的(2,3,4,8,9,10,14,15,16),同样的weight代表同样的颜色。
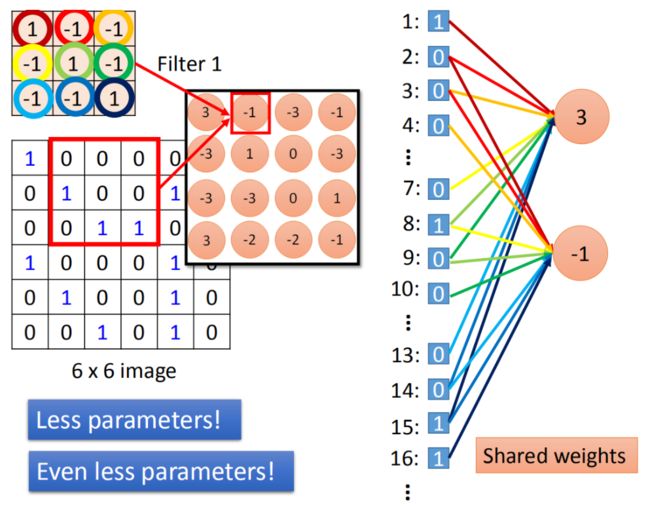
这两个neuron本来就在fully connect里面这两个neural本来是有自己的weight,当我们在做convolution时,首先把每一个neural连接的wight减少,强迫这两个neural共用一个weight。这件事就叫做shared weight,当我们做这件事情的时候,我们用的这个参数就比原来的更少。
Max pooling
相对于convolution来说,Max Pooling是比较简单的。我们根据filter 1得到4*4的maxtrix,根据filter2得到另一个4 *4的matrix,接下来把output ,4个一组。每一组里面可以选择它们的平均或者选最大的都可以,就是把四个value合成一个value。这个可以让你的image缩小。

假设我们选择四个里面的max vlaue保留下来,这样可能会有个问题,把这个放到neuron里面,这样就不能够微分了,但是可以用微分的办法来处理的。
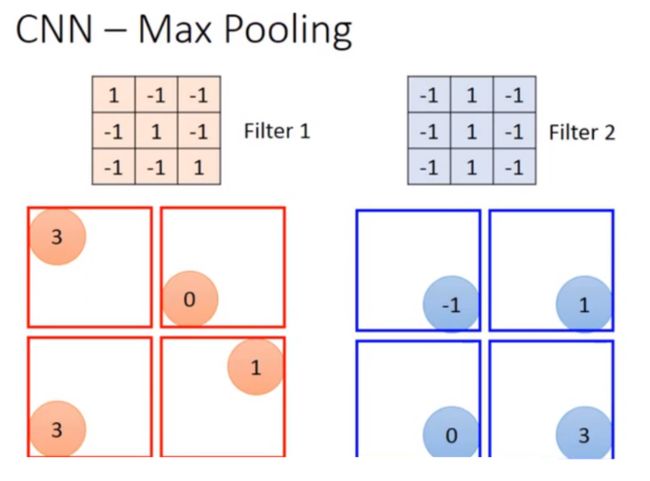
做完一个convolution和一次max pooling,就将原来6 * 6的image变成了一个2 *2的image。这个2 *2的pixel的深度depend你有几个filter(你有50个filter你就有50维),得到结果就是一个new image but smaller,一个filter就代表了一个channel。

这件事可以repeat很多次,通过一个convolution + max pooling就得到新的 image。它是一个比较小的image,可以把这个小的image,做同样的事情,再次通过convolution + max pooling,将得到一个更小的image。

假设第一层filter有2个,第二层的filter在考虑这个imput时是会考虑深度的,并不是每个channel分开考虑,而是一次考虑所有的channel。所以convolution有多少个filter,output就有多少个filter(convolution有25个filter,output就有25个filter。只不过,这25个filter都是一个立方体)。
Flattern
flatten就是feature map拉直,拉直之后就可以丢到fully connected feedforward netwwork,然后就结束了。

CNN in Keras
本来在DNN中input是一个vector,现在是CNN的话,会考虑 input image的几何空间的,所以不能给它一个vector。应该input一个tensor(高维的vector)。
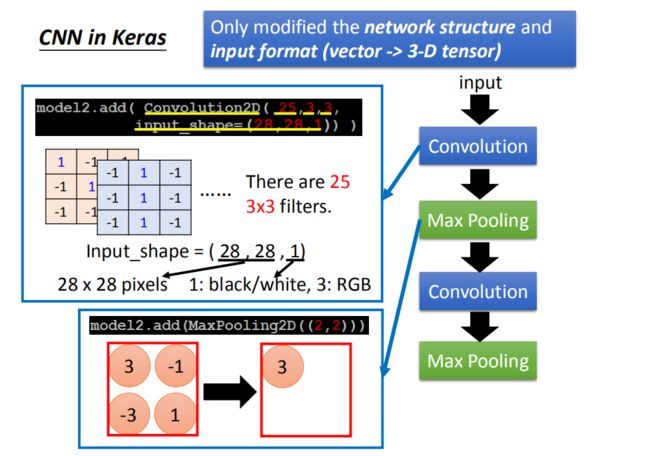
假设我们input一个1 *28 * 28的image,你就可以写model.add(Convolution2D( 25, 3, 3, Input_shape=(28,28,1)))。通过convplution以后得到output是25 *26 26(25个filter,通过3 *3得到26 * 26)。然后做max pooling,2 *2一组选择 max value得到 25 *13 * 13
然后在做一次convolution,假设我在这选50个filter,每一个filter是3 *3时,那么现在的channel就是50。13 *13的image通过3 *3的filter,就成11 *11,然后通过2 *2的Max Pooling,变成了50 *5 *5
在第一个convolution layer里面,每一个filter有9个参数,在第二个convolution layer里面,虽然每一个filter都是3 *3,但不是3 *3个参数,因为它input channel 是25个,所以它的参数是3 *3 *25(225)。

通过两次convolution,两次Max Pooling,原来是1 *28 *28变为50 *5 *5。flatten的目的就是把50 *5 *5拉直,拉直之后就成了1250维的vector,然后把1250维的vector丢到fully connected。

CNN学到了什么?
分析input第一个filter是比较容易的,因为一个layer每一个filter就是一个3*3的mmatrix,对应到3 *3的范围内的9个pixel。所以你只要看到这个filter的值就可以知道说:它在detain什么东西,所以第一层的filter是很容易理解的,但是你没有办法想要它在做什么事情的是第二层的filter。在第二层我们也是3 *3的filter有50个,但是这些filter的input并不是pixel(3 *3的9个input不是pixel)。而是做完convolution再做Max Pooling的结果。所以这个3 *3的filter就算你把它的weight拿出来,你也不知道它在做什么。另外这个3 *3的filter它考虑的范围并不是3 *3的pixel(9个pixel),而是比9个pxiel更大的范围。
第二个convolution layer里面的50个filter,每一个filter的output就是一个matrix(1111的matrix)。假设我们现在把第k个filter拿出来,它可能是这样子的(如图),每一个element我们就叫做 a i j k a_{ij}^k aijk(上标是说这是第k个filter,i,j代表在这个matrix里面的第i row和第j column)。

第k个filter被启动的Degree定义成:这个1111的 matrix里面全部的 element的summation。(input一张image,然后看这个filter output的这个11 *11的值全部加起来,当做是这个filter被active的程度)。若想知道第k个filter的作用是什么,找一张image,该image可以让第k个filter被activate的程度最大。用gradient ascent就可以做到(minimize使用gradient descent, maximize使用gradient ascent)。
把图像当成要找的参数x用gradient ascent做update,原来在train CNN network neural的时候,input是固定的,model的参数是用gradient descent来找出来的,用gradient descent找参数可以让loss被minimize。但是现在是反过来的,model参数是固定的,让gradient descent取update这个x,可以让这个activation function的Degree of the activation是最大的。
如果随便取12个filter出来,每一个filter都去找一张image,这个image可以让那个filter的activation最大。现在有50个filter,你就要去找50张image,它可以让这些filter的activation最大。图中是随便取前12个filter,让它最active的image。
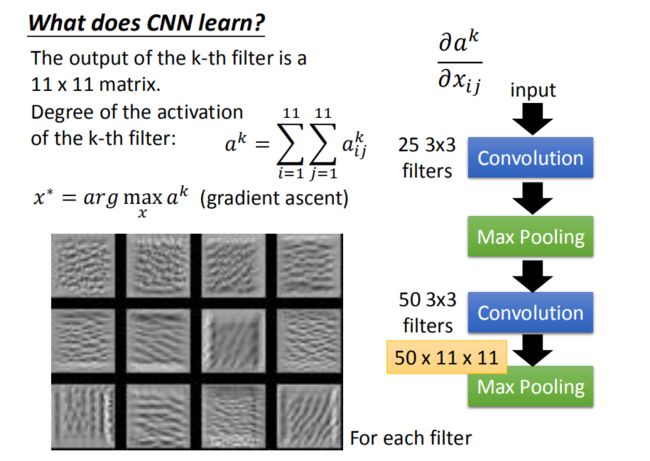
这些image有一个共同的特征就是:某种纹路在图上不断的反复。比如说第三张image,上面是有小小的斜条纹,意味着第三个filter的工作就是detain图上有没有斜的条纹。但每一个filter考虑的范围都只是图上一个小小的范围。所以一个图上如果出现小小的斜的条纹的话,这个filter就会被active,这个output的值就会比较大。那如果让图上所有的范围都出现这个小小的斜条纹的话,那这个时候它的Degree activation会是最大的。(因为它的工作就是侦测有没有斜的条纹,所以给它一个完整的数字的时候,它不会最兴奋。给它都是斜的条纹的时候,它是最兴奋的)。
所以每一个filter的工作就是detain某一张pattern。每一个filter所做的事情就是detain不同角度的线条,如果input有不同角度的线条,就会让某一个activation function,某一个filter的output值最大。
- 分析全连接层
在做完convolution和Max Pooling以后,要做一件事情叫做flatten,把flatten的结果丢到neural network里面去。在这个neural network里面,每一个neural的工作是什么?
定义第j个neural,它的output叫做 a j a_j aj。找一张image(用gradient ascent的方法找一张X),把这个image X丢到neural network里面去,它可以让 a j a_j aj的值被maximize。找到的结果就是这样的(如图)

filter观察到的是类似纹路的图案,在整张图上反复这样的纹路,那是因为每个filter考虑是图上一个小小的range(图上一部分range)。现在每一个neural,在做flatten以后,每个neural的工作就是去看整张图,而不是是去看图的一小部分。
output就是10维,每一维对应一个digit。把某一维拿出来,找一张image让那个维度output最大。现在找一张image,它可以让对应在数字1的output 最大,那么那张image显然就像看起来是数字1。但是实际上得到的结果是这样子的,每一张图分别代表数字0-9。output layer对应到0那个neuron,其实是这样的(如图),以此类推。

这个结果在很多的地方有已经被观察到了,今天的这个neuron network它所学到东西跟我们人类是不太一样的(它所学到的东西跟我们人类想象和认知不一样的)。 - 让图像更数字
假设image里面的每一个pixel用 x i j x_{ij} xij来表示,(每一个image有28 *28的pixel)我们把所有image上 i , j i,j i,j的值取绝对值后加起来。这一项就是L1-regularization。在找一个x可以让 y i y^i yi最大的同时让 ∣ x i j ∣ |x_{ij}| ∣xij∣的summation越小越好。也就是希望找出的image,大部分的地方是没有涂颜色的,只有非常少的部分是有涂颜色的。如果加上constraint以后得到的结果是这样的(如右图所示),跟左边的图比起来,隐约可以看出来它是一个数字(得到的结果看起来像数字)。

Deep Dream
给定一张image,将这张image丢到CNN中,把它的某一个hidden layer拿出来(vector),把positive dimension值调大,把negative dimension值调小(正的边 更大,负的变得更小)。把这个调节之后的vector当作是新的image的目标。然后找一张image(modify image),用GD方法,让它在hidden layer output是新设置的target。这样让CNN夸大化它所看到的东西,本来看起来是有点像的东西,它让某一个filter有被active,但是现在被active的更剧烈。
如果把一张image做Deep Dream处理,看到的结果是这样的。右边原来是一个石头,这个石头对机器来说,有点像熊,它就会强化这件事,所以它就真的变成了一只熊。
Deep Style
Deep Dream的进阶版是Deep Style。input一张image,input一张image,让machine去修改这张图,让它有另外一张图的风格 (类似于风格迁移)。
原来的image丢给CNN,然后得到CNN的filter的output,CNN的filter的output代表这张image有什么content。接下来把呐喊这张图也丢到CNN里面,也得到filter的output。我们并不在意一个filter ,而是在意filter和filter之间 的convolution,这个convolution代表了这张image的style。
用同一个CNN找一张image,这张image它的content像左边这张相片,但同时这张image的style像右边这张相片。找一张image同时可以maximize左边的图,也可以maximize右边的图。那得到的结果就是像最底下的这张图。用gradient ascent的方法找一张image,然后maximize这两张图,得到就是底下的这张图。

CNN的应用
-
围棋
如果让machine来下围棋,其实一般的topic neuron network也可以做到。只要learn一个network(也就是找一个function),它的input是棋盘,output是棋盘上的位置。即:根据这个棋盘的盘式,如果下一步要落子的话,你落子的位置其实就可以让machine学会。所以你用Fully-connected feedforward network也可以帮我们做到让machine下围棋这件事情。也就是你只要告诉input是一个19 *19的vector,每一个vector的dimension对应到棋盘上面的每一个位置。machine就可以学会下围棋了。 如果那个位置有一个黑子的话就是1,如果有一个白子的话就是-1,反之就是0。
半监督学习


虽然unlabel data只告诉我们了input,但unlabeled data的分布可以告诉我们一些事。那你可能会把boundary变为这样(斜线)。但是semi-supervised learning使用unlabel的方式往往伴随着一些假设,其实semi-supervised learning有没有用,是取决于你这个假设符不符合实际/精不精确。
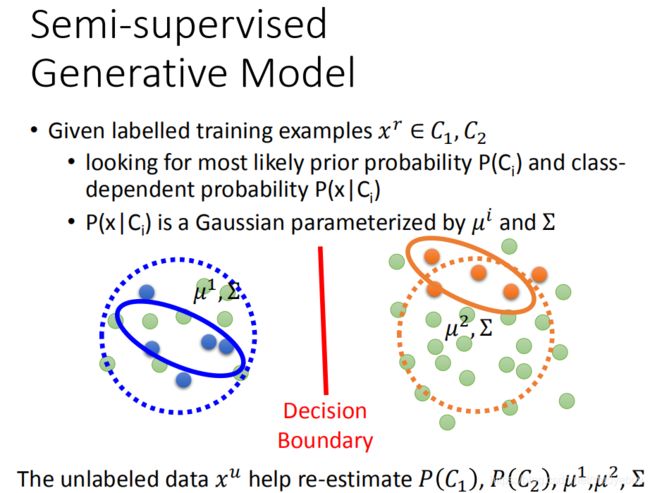
监督生成模型和半监督生成模型
假设:Low-density Separation
-
self-training
Low-density separation最简单的方法是self-training。self-training就是说,我们有一些label data并且还有一些unlabel data。接下来从label data中去train一个model,这个model叫做 f ∗ f^\ast f∗ ,根据这个 f ∗ f^\ast f∗ 去label你的unlabel data。你就把 x u x^u xu丢进 f ∗ f^\ast f∗ ,看它吐出来的 y u y^u yu是什么,那就是你的label data。那这个叫做pseudo-label。那接下来你要从你的unlabel data set中拿出一些data,把它加到labeled data set里面。然后再回头去train你的 f ∗ f^\ast f∗。

slef-training它很像generative model里面用的那个方法。他们唯一的差别就是在做self-training的时候,用的是hard label;做generative mode时,用的是soft model。在做self-training的时候我们会强制一笔train data是属于某一个class,但是在generative model的时候,根据它的posterior probability 它有一部分是属于class1一部分是属于class2。
假设我们用neural network,从 label data得到一笔network parameter( θ ∗ \theta^\ast θ∗)。现在有一笔unlabel data x u x^u xu,根据参数 θ ∗ \theta^\ast θ∗分为两类(0.7的几率是class1,0.3的几率是class2)。如果是hard label的话,把它直接label成class1,所以 x u x^u xu新的target第一维是1第二维是0(拿 x u x^u xutrain neural network)。如果去做soft的话。70 percent是属于class1,30percent是属于class2,那新的target是0.7跟0.3。在neural network中,soft这个方法是没有用的,一定要用hard label。因为本来输出就是0.7和0.3,目标又设成0.7和0.3,相当于自己证明自己,所以没用。用hard label的时候,就是用low-density separation的概念。也就是说: x u x^u xu它属于class1的几率只是比较高而已,我们没有很确定它一定是属于class1的,但这是一个非黑即白的世界,如果你看起来有点像class1,那就一定是class1。本来根据我的model说:0.7是class1 0.3是class2,那用hard label(low-density-separation)就改成它属于class1的几率是1(完全就不可能是class2)。soft是不会work的。

-
基于熵的正则化
如果用neural network,output是一个distribution,那不要限制这个output一定要是class1、class2,但是假设是这样的,这个output distribution一定要是很集中,因为这是一个非黑即白的世界。假设我们现在做五个class的分类,在class1的几率很大,在其他class的几率很小,这个是好的。在class5的几率很大,在其他class上几率很小,这也是好的。如果分布很平均,这样是不好的(因为这是一个非黑即白的世界),这不是符合low-density separation的假设。

但是现在的问题是怎样用数值的方法evaluate这个distribution是好的还是不好的。用的是entropy,算一个distribution的entropy,这个distribution entropy告诉你说:这个distribution到底是集中的还是不集中的。用一个值来表示distribution是集中的还是分散的,某一个distribution的entropy就是负的它对每一个class的几率乘以log class的几率。所以把第一个distribution的几率带到这个公式里面去,只有一个是1其他都是0,得到的entropy会得到是0( E ( y u ) = − ∑ m = 1 5 y m u ( l n y u ) E(y^u)=-\sum_{m=1}^{5}y^u_m(lny^u) E(yu)=−∑m=15ymu(lnyu),第二个也是0。第三个entropy是ln5ln5。散的比较开(不集中)entropy比较大,散的比较窄(集中)entropy比较小。
这个model的output在label data上分类整确,但在unlabel data上的entropy越小越好。所以根据这个假设,可以去重新设计loss function。原来的loss function是说:我希望找一个参数,让现在在label data上model的output跟正确的model output越小越好,可以cross entropy evaluate它们之间的距离,这个是label data的部分。在unlabel data的部分,会加上每一笔unlabel data的output distribution的entropy,希望这些unlabel data的entropy 越小越好。那么在这两个中间,可以乘以一个weight(ln5ln5)来考虑说:要偏向unlabel data多一点还是少一点。
在train的时候,用GD来一直minimize这件事情,没有什么问题的。unlabel data的角色就很像regularization,所以它被称之为 entropy-based regulariztion。之前说regularization是在原来的loss function后面加一个惩罚项(L2,L1),让它不要overfitting;现在加上根据unlabel data得到的entropy 来让它不要overfitting。 -
半监督SVM
SVM做的事情就是:给两个class的data,找一个boundary,这个boundary一方面要做有最大的margin(最大margin就是让这两个class分的越开越好)同时也要有最小的分类的错误。现在假设有一些unlabel data,semi-supervised SVM会穷举所有可能的label,就是这边有4笔unlabel data,每一笔它都可以是属于class1,也可以是属于class2,穷举它所有可能的label(如右图所示)。对每一个可能的结果都去做一个SVM,然后再去说哪一个unlabel data的可能性能够让margin最大同时又minimize error。
穷举所有的unlabel data label,这是非常多的事情。approximate的方法,一开始得到一些label,然后每次该一笔unlabel data看可不可以让margin变大,变大了就改一下。

Smoothness Assumption
![]()
假设x的分布是不平均的,它在某些地方是很集中,某些地方又很分散。如果 x 1 , x 2 x_1,x_2 x1,x2它们在high density region很close的话, y 1 , y 2 y^1,y^2 y1,y2才会是是很像的。 high density region可以用high density path做connection,举个例子,假设图中是data的分布,假设有三笔 d a t a ( x 1 , x 2 , x 3 ) data(x_1,x_2,x_3) data(x1,x2,x3)。如果考虑的是比较粗略的假设(相似的 x x x,那么output就很像,那 x 2 , x 3 x_2,x_3 x2,x3的label比较像,但 x 1 , x 2 x_1,x_2 x1,x2的label是比较不像),其实Smoothness Assumption更精确的假设是这样的,相似是要透过一个high density region。比如说, x 1 , x 2 x_1,x_2 x1,x2它们中间有一个high density region( x 1 , x 2 x_1,x_2 x1,x2)中间有很多很多的data,他们两个相连的地方是通过high density path相连的)。根据真正Smoothness Assumption的假设,它要告诉我们的意思就是说: x 1 , x 2 x_1,x_2 x1,x2是可能会有一样的label, x 2 , x 3 x_2,x_3 x2,x3可能会有比较不一样的label(他们中间没有high density path)。

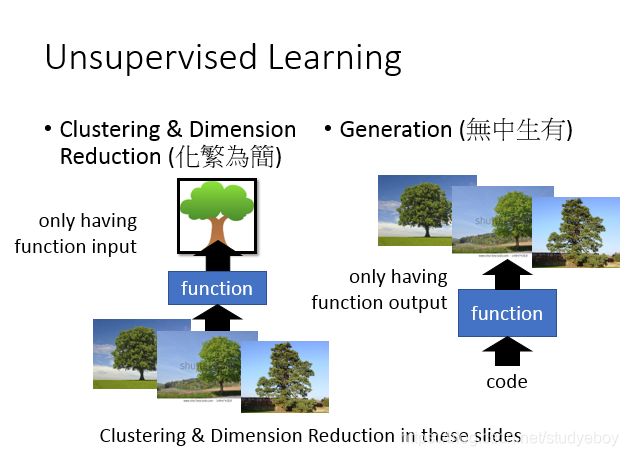
无监督学习
线性降维
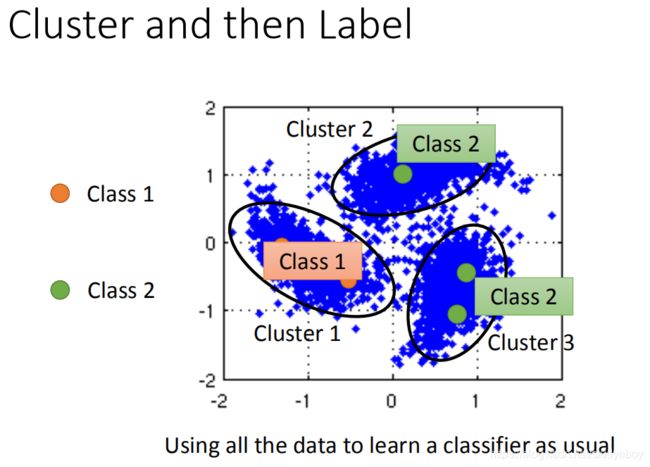
聚类
降维
-
特征选择
根据data在二维平面上的分布,发现data都集中在 x 2 x_2 x2 dimension这里, x 1 x_1 x1 dimension没有什么用,去掉 x 1 x_1 x1 dimension,保留 x 2 x_2 x2 dimension,就等于做到dimension reduction。这种方法不常用,因为很多时候任何一个dimension都不能去掉。

-
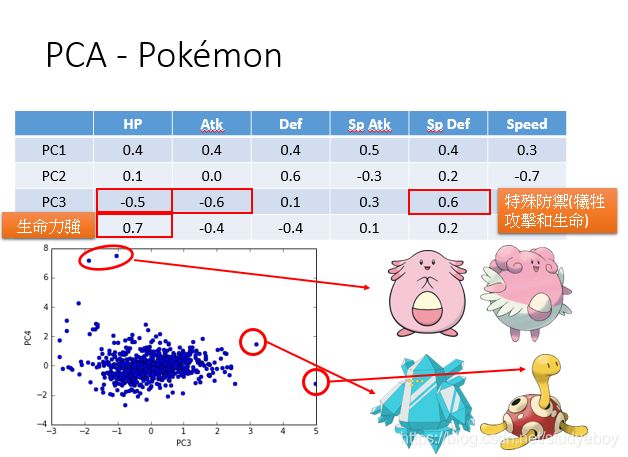
主成分分析
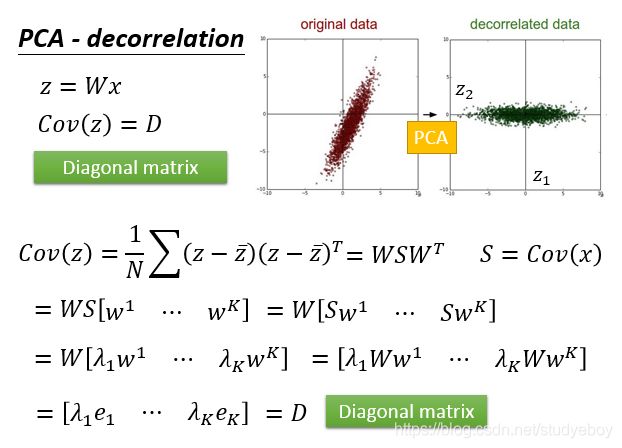
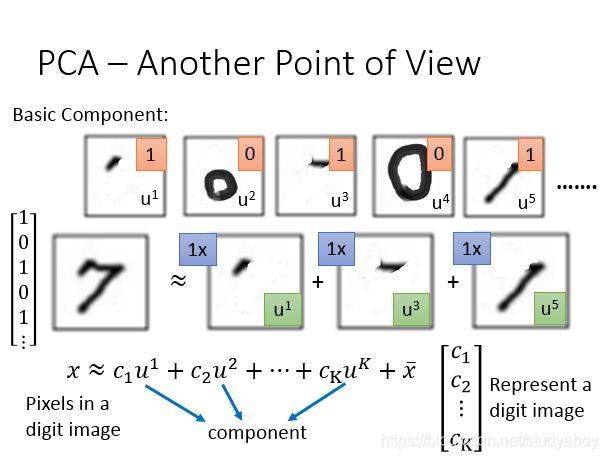
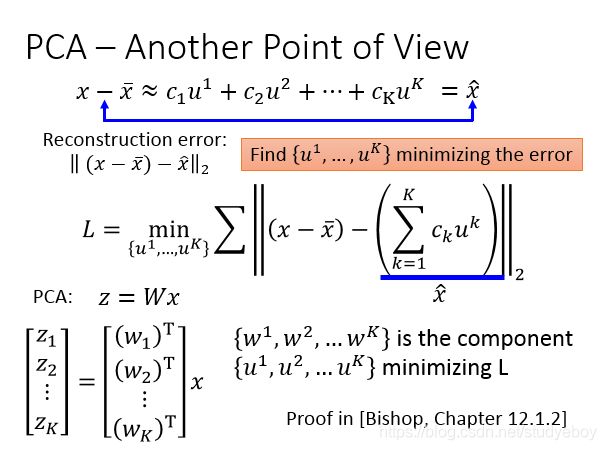
Principe component abalysis(PCA)是一个很简单linear function,input x和output z之间的关系是一个linear transform,input x乘上matrix w就得到它的output z。已知input x找matrix w。





词嵌入
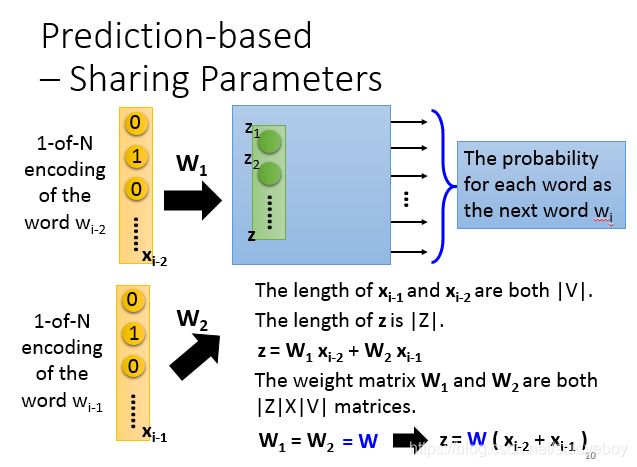
word embedding是dimension reduction的应用,用vector来表示word,最difficult的做法叫作1-of-N Encoding。每一个word用一个vector来表示,这个vector的dimension就是可能有的word的数目。假设有10w个word,那1-of-N Encoding的dimension就是10w维,每一个word就对应到其中一维。如果用这种方式来描述一个word,每一个word的vector都是不一样的,从这个vector中没有办法得到任何的咨询,例如cat跟dog都是动物这件事,没有办法知道。
把不同的word,但具有同样性质的word,用所属的class来表示,比如说dog和cat都是class1,ran、 jumped、 walk是class2,flower、tree、apple是class3。用class是不够,class1是动物,class2是动物可以做的行为,是有一些关联的,但是用class没法呈现出来。
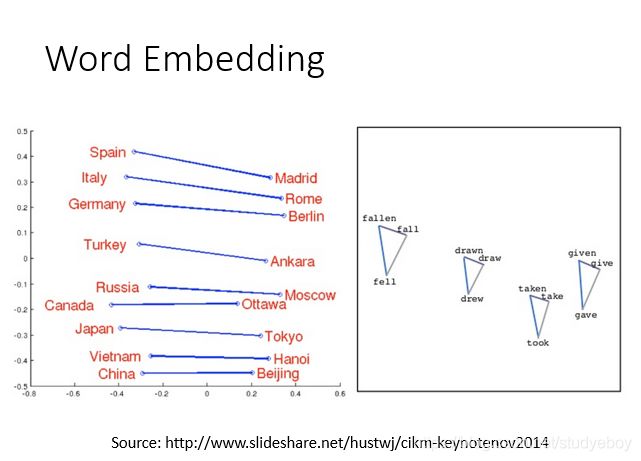
word Embedding把每一个word都project到high dimension space上面。在这个high dimension space里面,每一个dimension可能都有它特别的含义。

word Embedding是Unsupervised。只要让machine阅读大量的文章,它就可以知道每个词汇embedding feature vector是什么样子的。

learn一个neural network,找一个function,input一个词汇,output该词汇对应的word Embedding。找function的过程是一个Unsupervised的问题,因为input已知,output未知。
基于计数的词嵌入
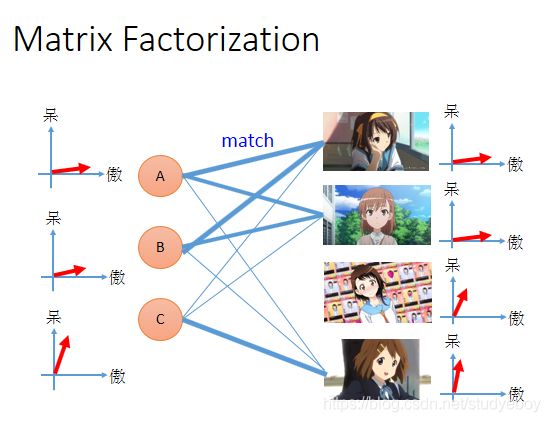
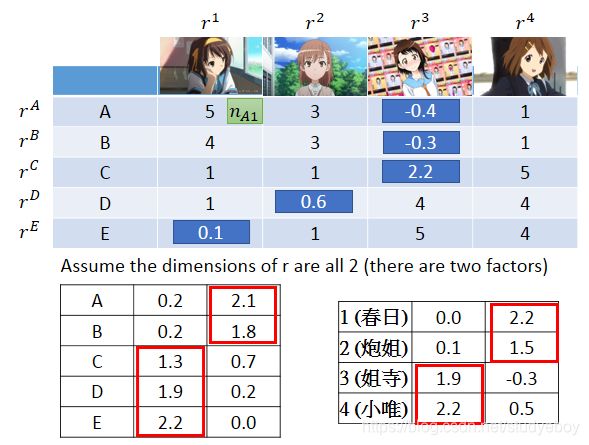
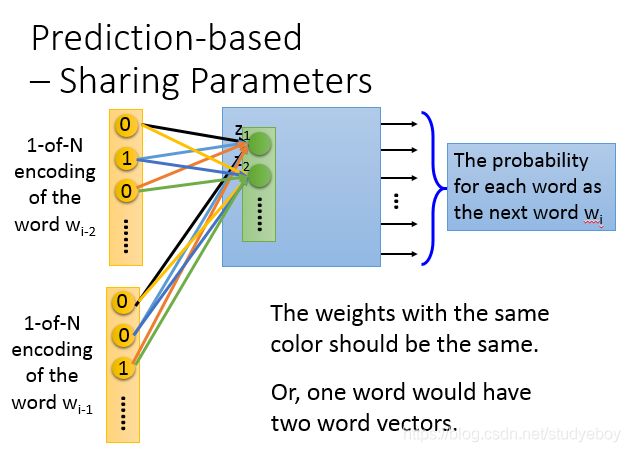
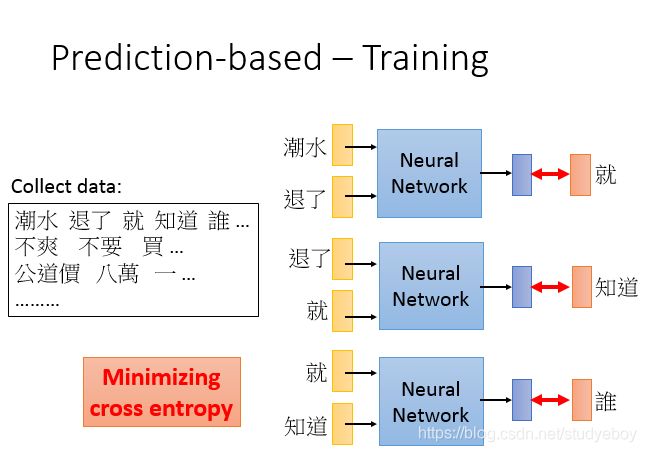
基于预测的词嵌入
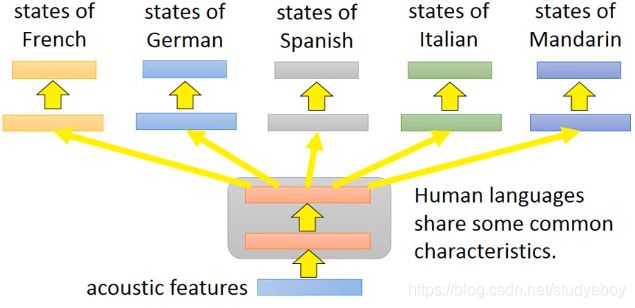
多语言嵌入
多域嵌入
文档嵌入
![]()
语义嵌入
Beyond Bag of Word
领域嵌入
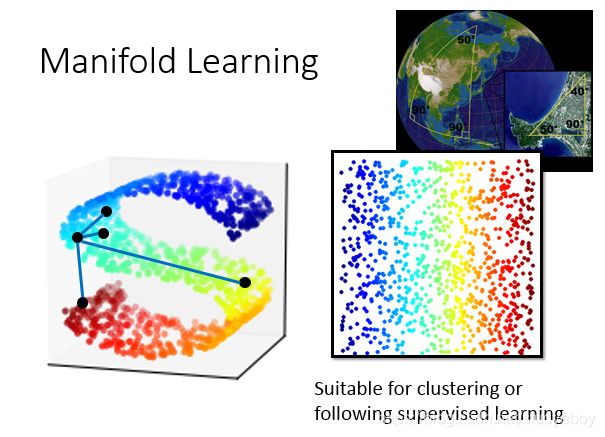
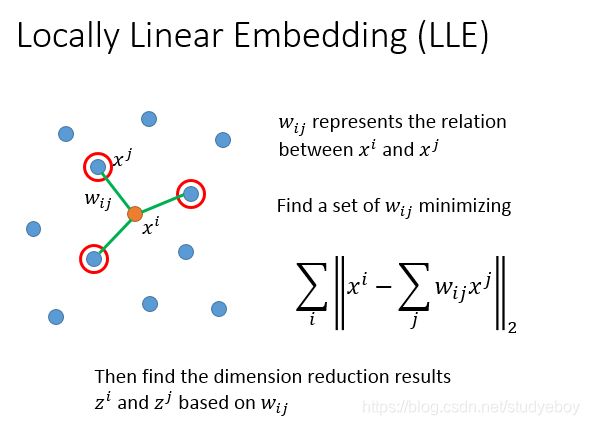
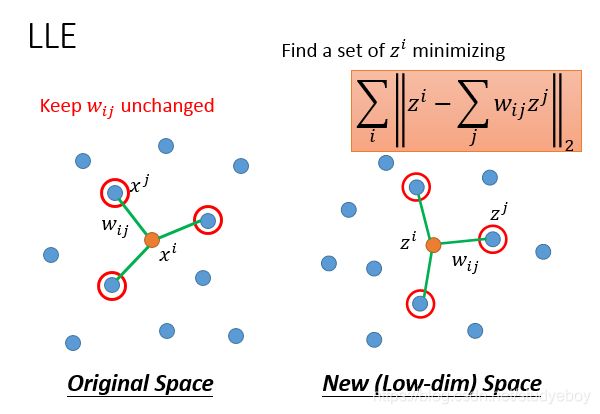
局部线性嵌入
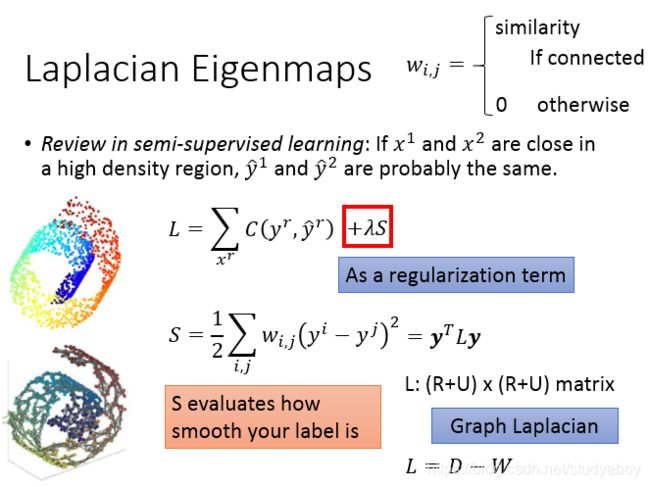
拉普拉斯特征映射
T-分布随机领域
它只假设相近的点应该要是接近的,但它没有假设说不相近的点没有要接近(不相近的点要分开)。比如说LLE在MNIST上你会遇到这样的情形:它确实会把同一个class聚集在一起,但它没有防止不同class的点不要叠成一团。

t-SNE也是在做降维,把原来的data point x变成low dimension vector z。衡量两个distribution之间的相似度呢?就是KL距离。

t-SNE会计算所有data point的similarity,所以它的运算有点大。在data point比较多的时候,t-SNE比较麻烦。第一个常见的做法是:先做降维,比如说:你原来的dimension很大,不会直接从很高的dimension直接做t-SNE,因为这样计算similarity时间会很长,通常会先用PCA做将降维,降到50维,再用t-SNE降到2维,这个是比较常见的做法。
如果给t-SNE一个新的data point,它是没办法做的。它只能够先给它一大群x,把每个x的z先找出来,但找完这些z以后,再给它一个新的x,要重新跑一遍这一整套演算法,所以就很麻烦。你有一大堆的x是high dimension,想要它在二维空间的分布是什么样子,用t-SNE,t-SNE会给不错的结果。

t-SNE这个similarity的选择是非常神妙的,在原来的data point space上面,evaluate similarity 是计算 x i , x j x^i,x^j xi,xj之间的Euclidean distance,取一个负号,再取exponent,这种方法比较好,因为它可以确保说只有非常相近的点才有值,exponential掉的比较快,只要距离一拉开,similarity就会变得很小。 在t-SNE之前,有一个方法叫做SNE:dimension reduction以后的space,它选择measure跟原来的space是一样的。t-SNE神妙的地方在:dimension reduction以后的space,它选择measure跟原来的space是不一样的,它在dimension reduction之后选的space是t distribution的其中一种( S ′ ( z i , z j ) = 1 1 + ∣ ∣ z i − z j ∣ ∣ 2 S^{'}(z^i,z^j)=\frac{1}{1+||z^i-z^j||_2} S′(zi,zj)=1+∣∣zi−zj∣∣21)。
假设横轴代表了在原来space上面的Euclidean distance或者是做dimension reduction以后的Euclidean distance。其中红色这条线是: e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 ) exp(-||x^i-x^j||_2) exp(−∣∣xi−xj∣∣2),蓝色这条线是: 1 1 + ∣ ∣ z i − z j ∣ ∣ 2 \frac{1}{1+||z^i-z^j||_2} 1+∣∣zi−zj∣∣21 。 图中的两个点做dimension reduction以后,要怎样才能维持它原来的space呢?变成图中这个样子。原来在高维空间里面,如果距离很近,那做完transform以后,它还是很近。原来就有一段距离,做完transform以后,会被拉的很远。

所以,t-SNE画出来的图往往长的这样,它会把你的data point 聚集成一群一群的,只要你的data point离的比较远,那做完t-SNE之后,就会强化,变得更远了。

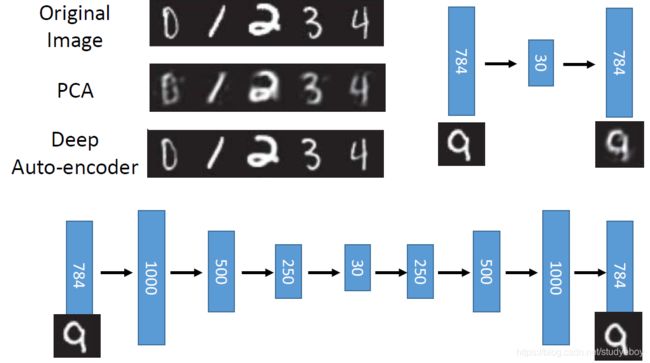
深度自编码器
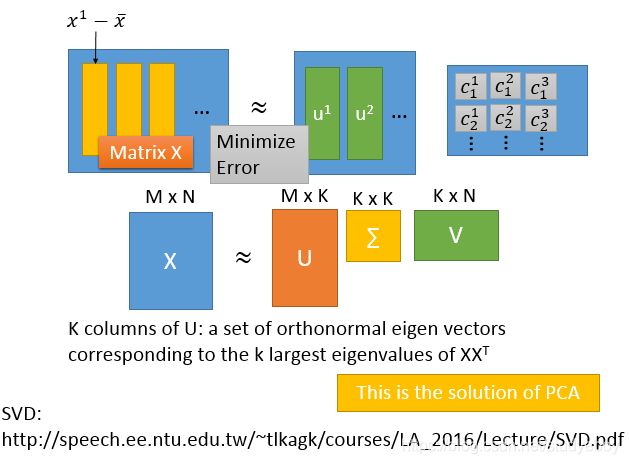
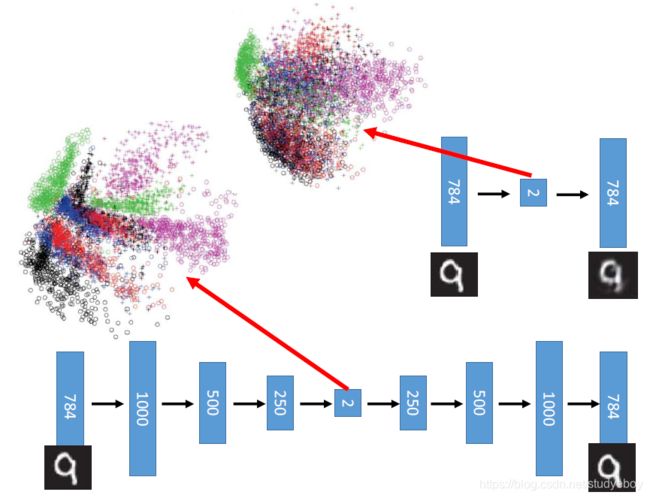
Recap:PCA
deep 自动编码器
自动编码器—文本检索
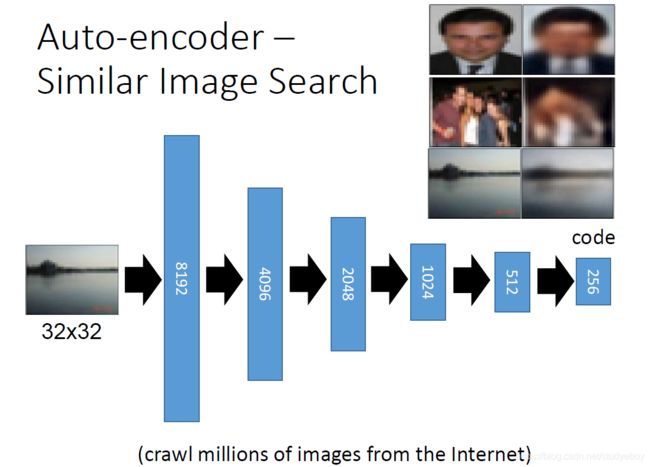
自动编码—类似图像搜索
CNN自动编码
自动编码—预训练DNN
深度生成模型I
PixelRNN
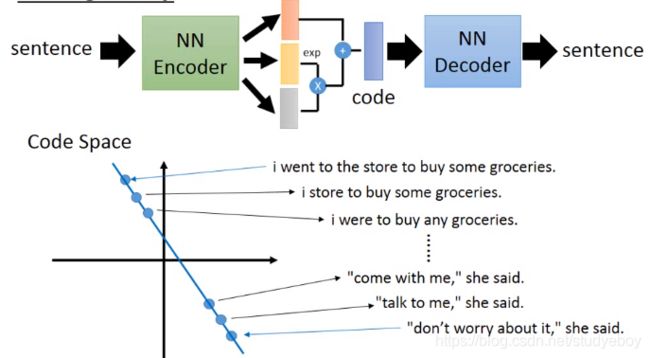
自动编码器
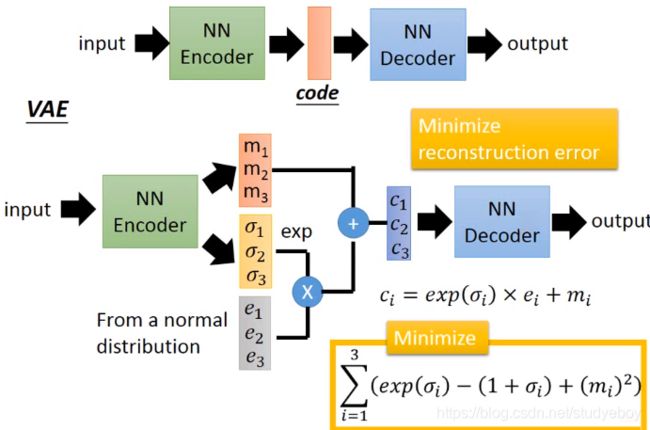
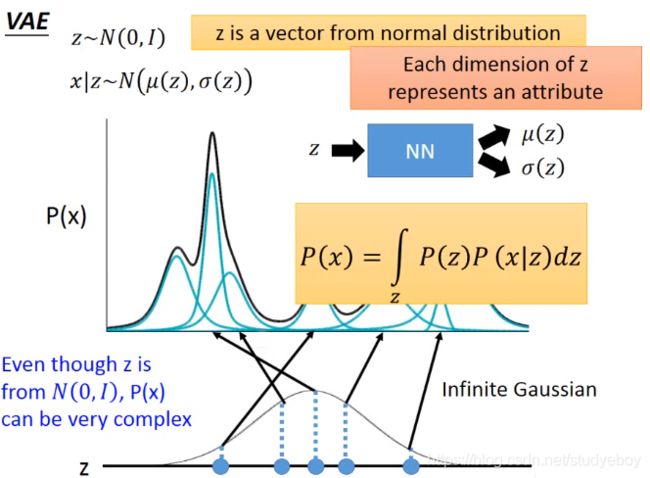
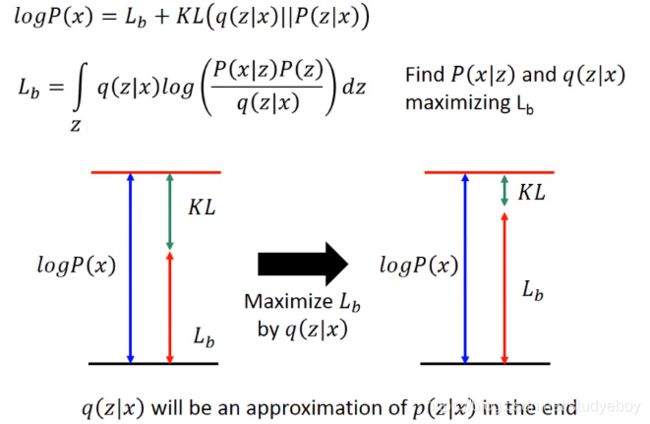
Variational Autoencoder(VAE)
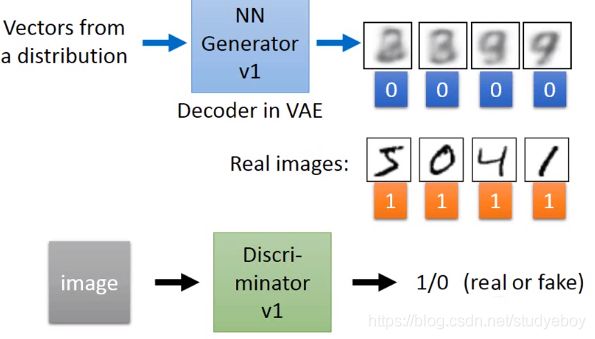
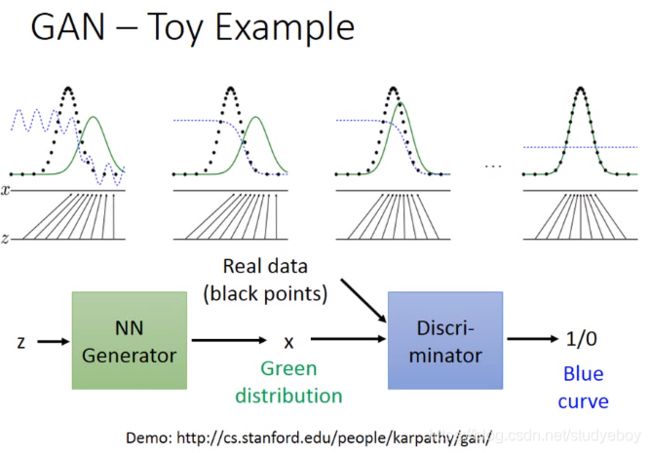
Generative Adversarial Network(GAN)
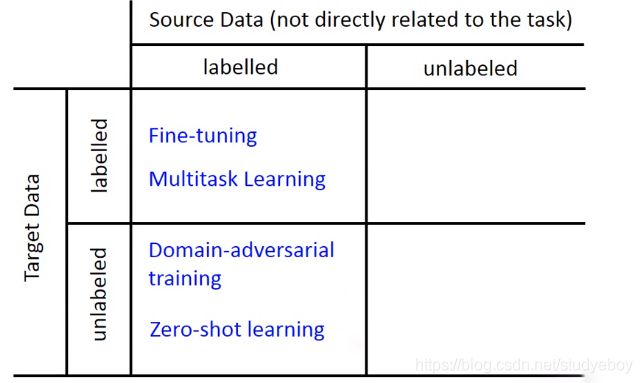
迁移学习
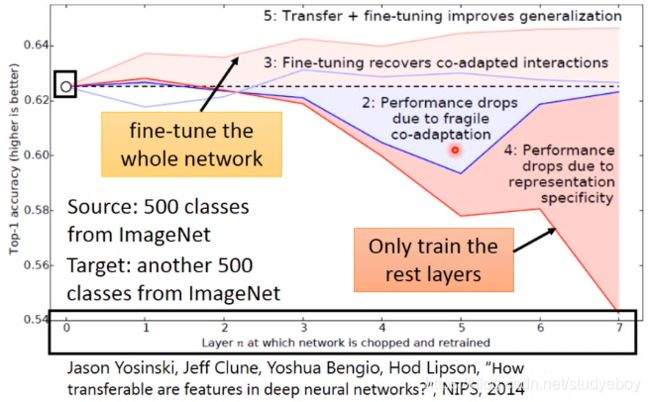
模型微调
保守训练
层迁移
多任务学习
渐进神经网络
神经网络的领域对抗训练
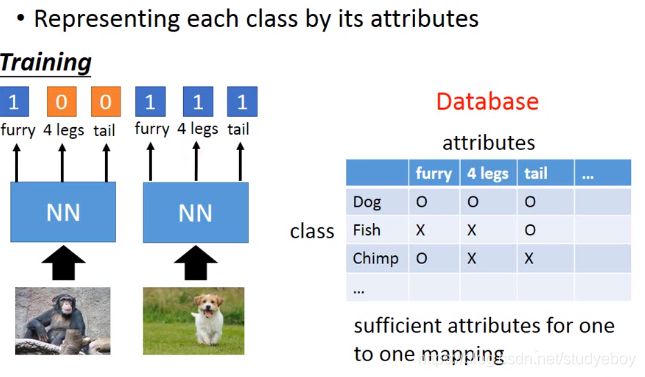
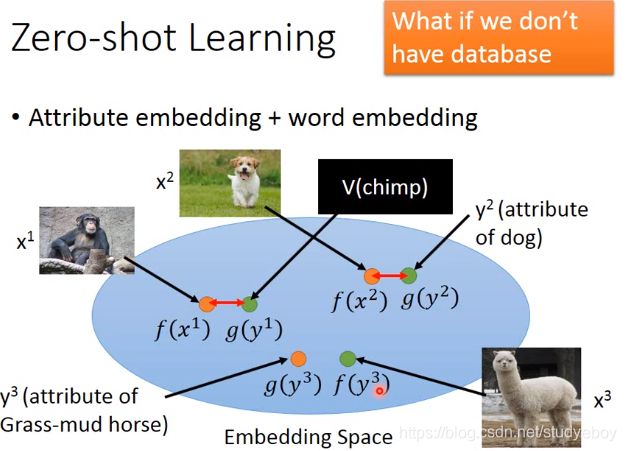
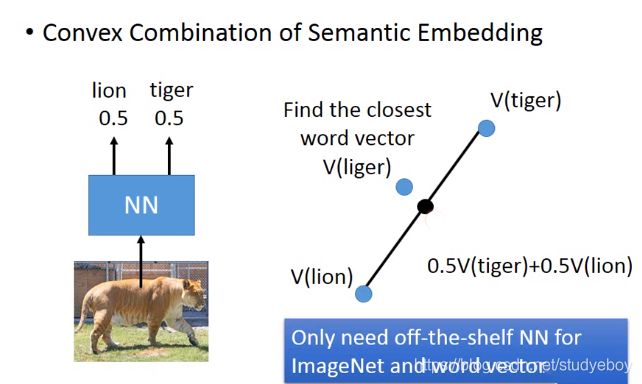
零样本学习
自我学习&自我聚类
支持向量机
机器学习
-
函数集
定义一个函数为 g ( x ) g(x) g(x),这个 g ( x ) g(x) g(x)它里面有另外一个function。

-
损失函数





线性SVM
-
Loss function

∑ n l ( f ( x n ) , y ^ n ) \sum_nl(f(x^n), \hat y ^ n) ∑nl(f(xn),y^n) 为凸函数, λ ∥ w ∥ 2 \lambda \|w\|_{2} λ∥w∥2也为凸函数。两者相加之和也为凸函数。表面上看是不可微分的,但是实际上是可以使用梯度下降做优化器。 -
另一种表述


核方法
- 对偶性
实际上是最小化损失函数的权重参数 w ∗ w^{*} w∗ 可以表示为数据点 x n x^{n} xn的线性组合。这里从另外的角度解释。 Linear SVM也可以用梯度下降来更新参数,

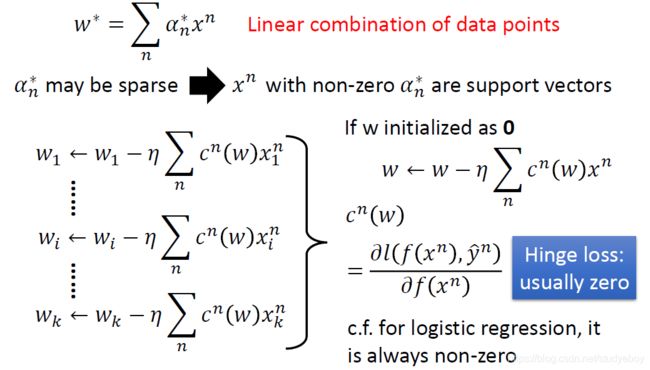
根据前面得到的公式,每次更新权重都加上 x n x^{n} xn的线性组合,那么如果 w w w初始化为0向量的话,得到的 w w w就是 x n \boldsymbol{x}^{n} xn的线性组合。其中的权重 c n ( w ) c^{n}(w) cn(w)是损失函数 l ( f ( x n ) , y ^ n ) l\left(f\left(x^{n}\right), \hat{y}^{n}\right) l(f(xn),y^n)对 f ( x n ) f\left(x^{n}\right) f(xn)的偏导数。 如果损失函数采用的是Hinge Loss, c n ( w ) c^{n}(w) cn(w)往往就是0,不是所有的 x n x_n xn都会拿来加到 w w w里面去的,从而 α n ∗ \alpha_{n}^{*} αn∗可能是稀疏的,就是有的数据点对应的 α n ∗ \alpha_{n}^{*} αn∗可能是0, 具有非零 α n ∗ \alpha_{n}^{*} αn∗的数据点 x n x^{n} xn是支持向量。这样的好处是模型比较鲁棒:不是支持向量的数据点,就算去掉也不会对结果有影响,异常点只要不是支持向量,就不会对结果有影响。反观logistic regression(用cross entropy作损失函数),它在更新参数时的权重就不是稀疏的,所以每笔data都对结果有影响。 - 函数集
把 w w w写成 x n x^n xn的线性组合,最大的好处是可以使用kernel trick。

f(x) 可写为 f ( x ) = Σ n α n ( x n ⋅ x ) f(x)=\Sigma_{n} \alpha_{n}\left(x^{n} \cdot x\right) f(x)=Σnαn(xn⋅x),由于用的损失函数是Hinge Loss, 所以 α n \alpha_{n} αn是稀疏的,只需要算支持向量(即不为0的 x x x)与数据点 x x x之间的内积即可。

可以把内积 ( x n ⋅ x ) \left(x^{n} \cdot x\right) (xn⋅x)写作核方法 K ( x n , x ) K\left(x^{n}, x\right) K(xn,x)这样,整体损失函数可以改写为图中的式子,我们只需要知道核函数 K ( x , z ) K(x, z) K(x,z)即可,这就叫核技巧。 - 损失函数+训练
找到一组 [ α 1 ⋯ α N ] \left[\begin{array}{lll}{\alpha_{1}} & {\cdots} & {\alpha_{N}}\end{array}\right] [α1⋯αN],使得损失函数最小。

这样的好处就是不需要真正知道 x x x,只需要知道 x x x和 z z z的内积。这叫做Kernel trick,Kernel trick不只可用于SVM,也可用于逻辑回归,线性回归等。(图中”project”应改为”product”)。
核技巧
当我们将所有 x x x转换为 ϕ ( x ) \phi(x) ϕ(x)时,内核技巧很有用, ϕ ( x ) \phi(x) ϕ(x)是 x x x做feature transformation后的结果, ,将 k k k维投影到更高维,每个维度考虑所有feature两两之间的关系。

直接计算 K ( x , z ) K(x, z) K(x,z)有时可能比“特征变换+内积”更快。 假设 x , z x,z x,z不是2维,而是高维,想要将它投影到更高的一个空间,就会考虑所有点 两两之间的关系,如果使用的是和方法的话,可以轻易的算出 K ( x , z ) K(x, z) K(x,z)

-
径向基函数
RBF Kernel, x x x与 z z z越像,则 K ( x , z ) K(x, z) K(x,z)越大。它是两个无穷维特征向量的内积。将核函数展开并使用泰勒级数,可见核函数是无穷项之和,每项都可写成内积形式,将与 x , z x,z x,z有关的向量分别串起来,得到两个无穷维的向量,这两个向量的内积就是RBF核函数。由于使用了无穷维的特征,在用RBF核函数时要小心过拟合(可能在训练集上得到很好的performance, 而在testing data 上得到很糟的performance)。

-
sigmoid核
Sigmoid Kernel. (图中 α n , α 1 , α 2 \alpha^{n}, \alpha^{1}, \alpha^{2} αn,α1,α2应改为 α n , α 1 , α 2 \alpha^{n}, \alpha^{1}, \alpha^{2} αn,α1,α2). sigmoid kernel可看做一个单隐层网络,神经元个数就是支持向量个数,神经元权重就是支持向量各维度的数值。
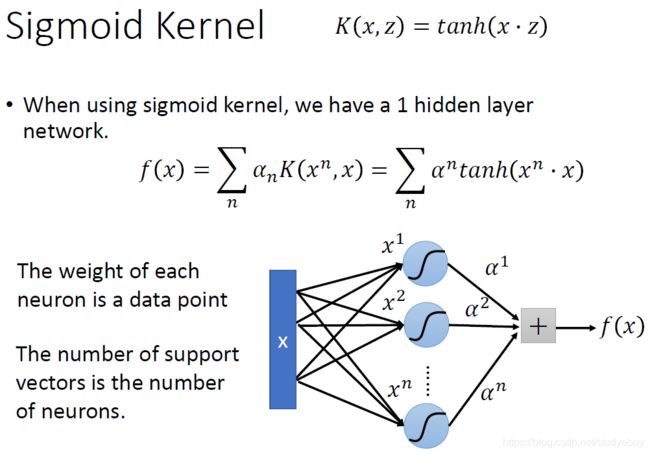
我们可以直接设计 K ( x , z ) K(x, z) K(x,z)而不是考虑 ϕ ( x ) \phi(x) ϕ(x), ϕ ( z ) \phi(z) ϕ(z),因为当 x x x是像序列这样的结构化对象时,难以设计 ϕ ( x ) \phi(x) ϕ(x),核方法的好处就是可以直接去设计核函数不用考虑 x x x和 z z z的特征长什么样。
SVM其他变形
- Support Vector Regression(SVR)
- Ranking SVM
- One-class SVM
结构化学习
- 输入输出都是一种带有结构的对象
- 对象:sequence、list、tree、bounding box
应用:
- Speech recognitian(语音辨识)
input 是一个signal sequence,output是另一个text sequence - Translation(翻译)
input 是一种语言的sequence,output是另外一种语言的sequence - Syntatic Paring(文法解析)
input 是一个sentence,output 是一个文法解析树 - Object Detection(目标检测)
input 是一张image,output是一个bounding box。用这个bounding box把这个object给框出来。 - Summarization
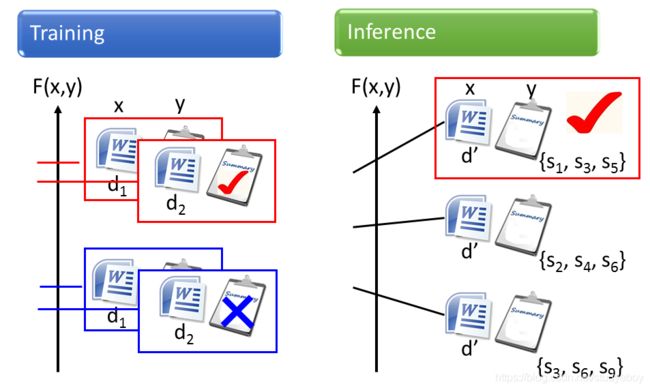
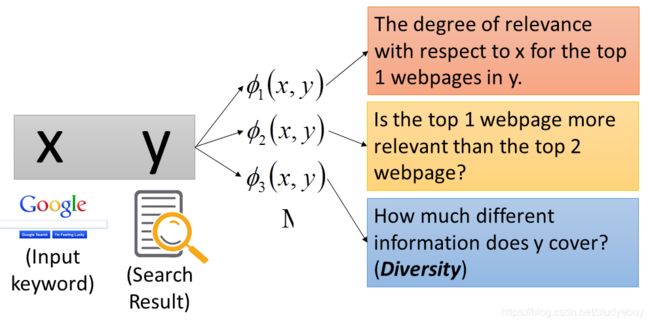
input是一个大的document,output是一个summary。input 和output都是一个sequence。 - Retrieval
input是搜寻的关键词,output是搜寻的结果,是一个webpage的list。
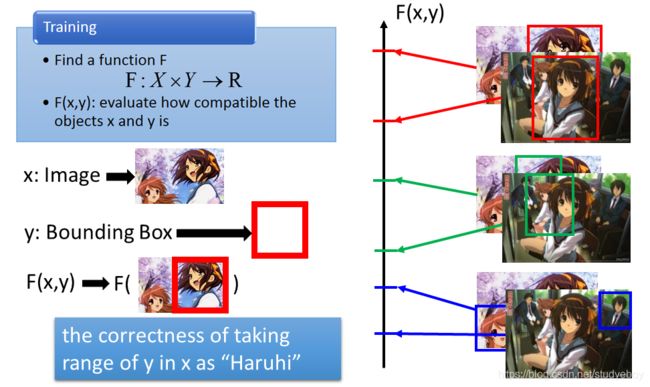
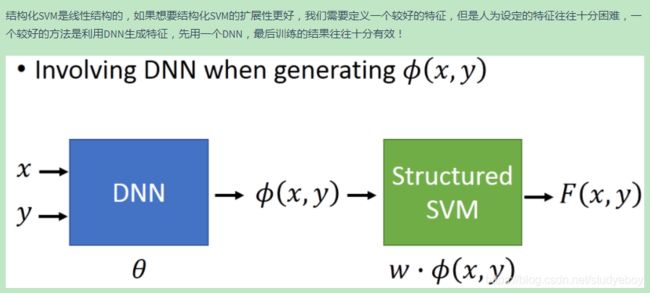
只要解出这三个问题,就可以做Structured Learning。 这三个问题可以跟HMM的三个问题联系到一起,也可以跟DNN联系到一起,比如说现在要做手写数字辨识,input一个image,把它分成10类,那F长什么样子呢,先把x扔进一个DNN,得到一个N(x),接下来再input y,y是一个vector,把这个y和N(x)算cross entropy,negative 这个CE(N(x),y)就是F(x,y)。
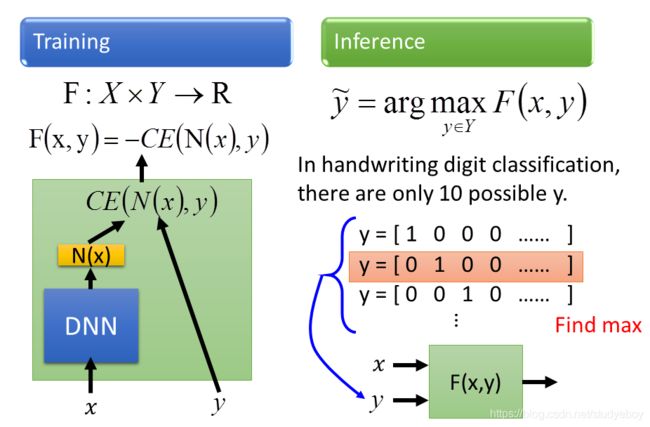
线性模型

假如第一Problem中的F(x,y)有一种特殊的形式,那么第三个Problem就不是个问题。
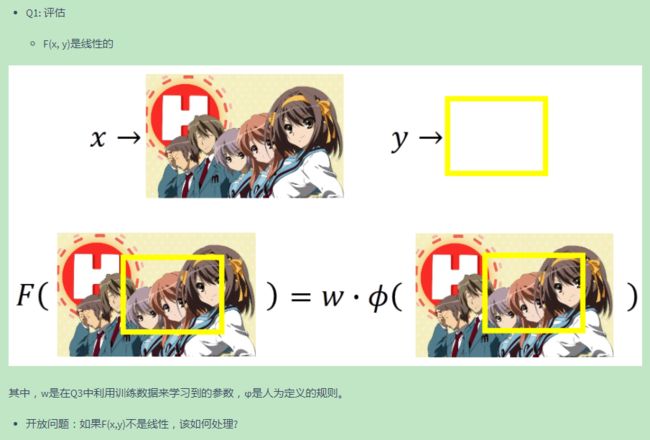
Evaluation问题
如果special form必须是Linear,也就是说一个 ( x , y ) (x,y) (x,y)的pair,首先用一组特征来描述 ( x , y ) (x,y) (x,y)的pair,其中 ϕ i \phi_{i} ϕi代表一种特征,也就说 ( x , y ) (x,y) (x,y)具有特征 ϕ 1 \phi_1 ϕ1是 ϕ 1 ( x , y ) \phi_1(x,y) ϕ1(x,y)这个值,具有特征 ϕ 2 \phi_2 ϕ2是 ϕ 2 ( x , y ) \phi_2(x,y) ϕ2(x,y)这个值,等等。然后F(x,y)它长得什么样子呢?
F ( x , y ) = w 1 ϕ 1 ( x , y ) + w 2 ϕ 2 ( x , y ) + w 3 ϕ 3 ( x , y ) + . . . F(x,y)=w_1\phi_1(x,y)+w_2\phi_2(x,y)+w_3\phi_3(x,y)+... F(x,y)=w1ϕ1(x,y)+w2ϕ2(x,y)+w3ϕ3(x,y)+...
向量形式可以写为 F ( x , y ) = w T ϕ ( x , y ) F(x,y)=\mathbf{w}^T\phi(x,y) F(x,y)=wTϕ(x,y)
Inference问题
本来这个 F ( x , y ) = w ⋅ ϕ ( x , y ) F(x,y)=w \cdot \phi(x,y) F(x,y)=w⋅ϕ(x,y) 但是我们一样需要去穷举所有的 y y y, y = a r g max y ∈ Y w ⋅ ϕ ( x , y ) y = arg \max _{y \in Y}w \cdot \phi(x,y) y=argmaxy∈Yw⋅ϕ(x,y) 来看哪个 y y y可以让 F ( x , y ) F(x,y) F(x,y)值最大。这个怎么办呢?假设这个问题已经被解决的样子。
Training问题
假装第二个问题已经被解决的情况下,我们就进入第三个问题。有一堆的Training data: { ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , . . . , ( x r , y ^ r , . . . ) } \{(x^1,\hat{y}^1),(x^2,\hat{y}^2),...,(x^r,\hat{y}^r,...)\} {(x1,y^1),(x2,y^2),...,(xr,y^r,...)},希望找到一个 f u n c t i o n F ( x , y ) function F(x,y) functionF(x,y),其实是希望找到一个 w w w,怎么找到这个 w w w使得以下条件被满足

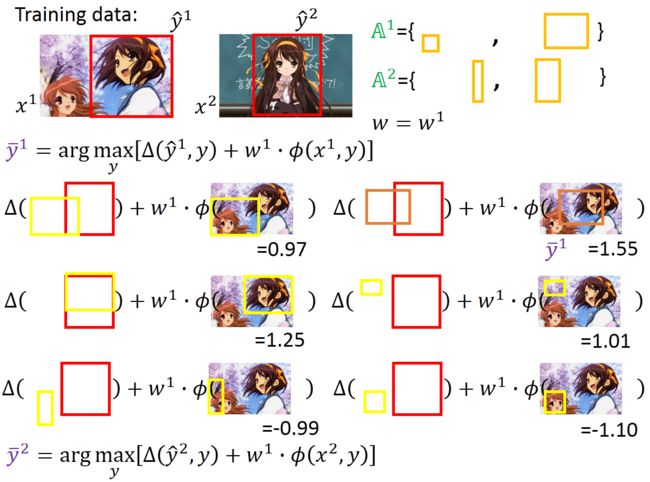
对所有的training data而言,希望正确的 w ⋅ ϕ ( x r , y ^ r ) w\cdot \phi(x^r,\hat{y}^r) w⋅ϕ(xr,y^r)应该大过于其他的任何 w ⋅ ϕ ( x r , y ) w\cdot \phi(x^r,y) w⋅ϕ(xr,y)。用比较具体的例子来说明,假设我现在要做的object detection,我们收集了一张image x 1 x^1 x1,知道 x 1 x^1 x1 所对应的 y ^ 1 \hat{y}^1 y^1 ,我们又收集了另外一张图片,对应的框框也标出。两张如下图所示
对于第一张图,我们假设 ( x 1 , y ^ 1 ) (x^1,\hat{y}^1) (x1,y^1)所形成的feature是红色 ϕ ( x 1 , y ^ 1 ) \phi(x^1,\hat{y}^1) ϕ(x1,y^1)这个点,其他的y跟x所形成的是蓝色的点。如下图所示

红色的点只有一个,蓝色的点有好多。 ( x 2 , y ^ 2 ) (x^2,\hat{y}^2) (x2,y^2)所形成的feature是红色的星星, x 2 x^2 x2 与其他的 y y y所形成的是蓝色的星星。可以想象,红色的星星只有一个,蓝色的星星有无数个。把它们画在图上,假设它们是如下图所示位置

我们所要达到的任务是,希望找到一个 w w w,那这个 w w w可以做到什么事呢?我们把这上面的每个点,红色的星星,红色的圈圈,成千上万的蓝色圈圈和蓝色星星通通拿去和 w w w做inner cdot后,得到的结果是红色星星所得到的大过于所有蓝色星星,红色的圈圈大过于所有红色的圈圈所得到的值。不同形状之间我们就不比较。圈圈自己跟圈圈比,星星自己跟星星比。也就是说希望正确的答案结果大于错误的答案结果,即 w ⋅ ϕ ( x 1 , y ^ 1 ) ≥ w ⋅ ϕ ( x 1 , y 1 ) , w ⋅ ϕ ( x 2 , y ^ 2 ) ≥ w ⋅ ϕ ( x 2 , y 2 ) w \cdot \phi(x^1,\hat{y}^1) \geq w \cdot \phi(x^1,y^1),w \cdot \phi(x^2,\hat{y}^2) \geq w \cdot \phi(x^2,y^2) w⋅ϕ(x1,y^1)≥w⋅ϕ(x1,y1),w⋅ϕ(x2,y^2)≥w⋅ϕ(x2,y2)。
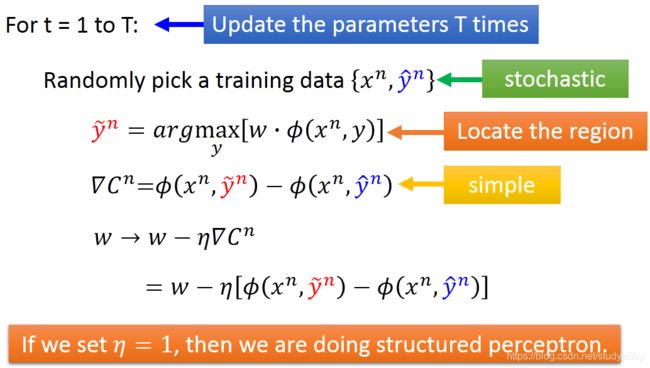
我们提供一个演算法。 输入:训练数据 { ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , . . . , ( x r , y ^ r ) , . . . } \{(x^1,\hat{y}^1),(x^2,\hat{y}^2),...,(x^r,\hat{y}^r),...\} {(x1,y^1),(x2,y^2),...,(xr,y^r),...}输出:权重向量 w w w 算法:

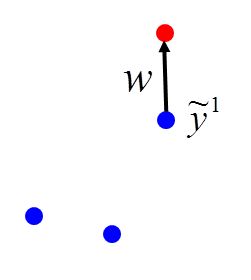
这个演算法的input就是我们的training data,output就是要找到一个vector w w w,这个vector w w w要满足我们之前所说的特性。一开始,我们先initialize w = 0 w=0 w=0,然后开始跑一个外围圈,这个外围圈里面,每次我们都取出一笔training data ( x r , y ^ r ) (x^r,\hat{y}^r) (xr,y^r),然后我们去找一个 y ~ r \tilde{y}^r y~r,它可以使得 w ⋅ ( x r , y ) w \cdot (x^r,y) w⋅(xr,y)的值最大,这个问题其实就是Problem 2,我们刚刚假设这个问题已经解决了的,如果找出来的 y ~ r \tilde{y}^r y~r不是正确答案,即 y ~ r ≠ y ^ r \tilde{y}^r \neq \hat{y}^r y~r=y^r,代表这个 w w w不是我要的,就要把这个 w w w改一下,把 ϕ ( x r , y ^ r ) \phi(x^r,\hat{y}^r) ϕ(xr,y^r)计算出来,把 ϕ ( x r , y ~ r ) \phi(x^r,\tilde{y}^r) ϕ(xr,y~r)也计算出来,两者相减在加到 w w w上,update w w w,有新的 w w w后,再去取一个新的example,然后重新算一次max,如果算出来不对再update,步骤一直下去,如果我们要找的 w w w是存在得,那么最终就会停止。
这不就是perceptron algorithm,perceptron learning 其实也是structured learning 的一个特例,以下证明几乎是一样。举个例子来说明一下,刚才那个演算法是怎么运作的。我们的目标是要找到一个 w w w,它可以让红色星星大过蓝色星星,红色圈圈大过蓝色圈圈,假设这个 w w w是存在的,首先我们假设 w = 0 w=0 w=0,然后我们随便pick 一个example ( x 1 , y ^ 1 ) (x^1,\hat{y}^1) (x1,y^1),根据我手上的data 和 w w w 去看 哪一个 y ~ 1 \tilde{y}^1 y~1使得 w ⋅ ϕ ( x 1 , y ) w \cdot \phi(x^1,y) w⋅ϕ(x1,y)的值最大,现在 w = 0 w=0 w=0,不管是谁,所算出来的值都为0,所以结果值都是一样的,那么没关系,我们随机选一个 y y y当做 y ~ 1 \tilde{y}^1 y~1 就可以。我们假设选了下图红框标出的点作为 y ~ 1 \tilde{y}^1 y~1 ,选出来的 y ~ 1 ≠ y ^ 1 \tilde{y}^1 \neq \hat{y}^1 y~1=y^1,对 w w w进行调整,把 ϕ ( x r , y ^ r ) \phi(x^r,\hat{y}^r) ϕ(xr,y^r)值减掉 ϕ ( x r , y ~ r ) \phi(x^r,\tilde{y}^r) ϕ(xr,y~r)的值再和 w w w加起来,更新 w w w
w → w + ϕ ( x 1 , y ^ 1 ) − ϕ ( x 1 , y ~ 1 ) ( 2 ) w \rightarrow w + \phi(x^1,\hat{y}^1) -\phi(x^1,\tilde{y}^1) (2) w→w+ϕ(x1,y^1)−ϕ(x1,y~1)(2)
我们就可以获取到第一个 w w w,第二步呢,我们就在选一个example ( x 2 , y ^ 2 ) (x^2,\hat{y}^2) (x2,y^2),穷举所有可能的 y y y,计算 w ⋅ ϕ ( x 2 , y ) w \cdot \phi(x^2,y) w⋅ϕ(x2,y),找出值最大时对应的 y y y,假设为下图的 y ~ 2 \tilde{y}^2 y~2 ,发现不等于 y ^ 2 \hat{y}^2 y^2,按照公式(2)更新 w w w,得到一个新的 w w w。然后再取出 ( x 1 , y ^ 1 ) (x^1,\hat{y}^1) (x1,y^1),得到 y ~ 1 = y ^ 2 \tilde{y}^1=\hat{y}^2 y~1=y^2 ,对于第一笔就不用更新。再测试第二笔data,发现 y ~ 1 = y ^ 2 \tilde{y}^1 = \hat{y}^2 y~1=y^2 , w w w也不用更新,等等。看过所有data后,发现 w w w不再更新,就停止整个training。所找出的 w w w可以让 y ~ r = y ^ r \tilde{y}^r = \hat{y}^r y~r=y^r。接下来就证明这个演算法的收敛性。

结构化支持向量机
结构化要解决的问题
统一框架:两步走,三问题
两步走:
![]()
三问题:
![]()
示例:目标检测



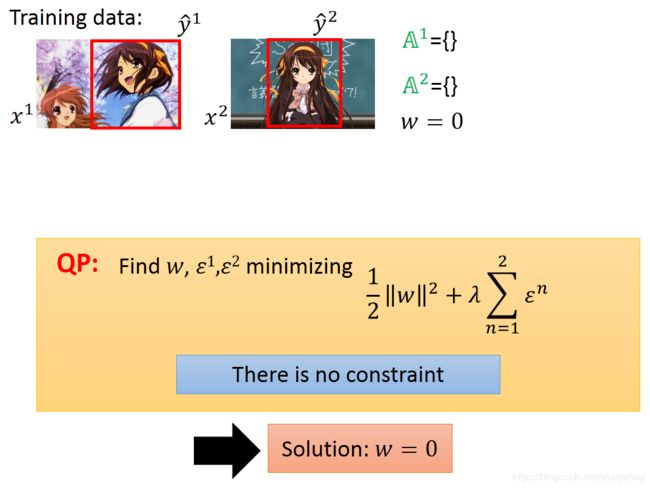
可分情形
存在一个权值向量 w ^ \hat{w} w^
,使得:
w ^ ⋅ ϕ ( x 1 , y ^ 1 ) ≥ w ^ ⋅ ϕ ( x 1 , y ) + δ w ^ ⋅ ϕ ( x 2 , y ^ 2 ) ≥ w ^ ⋅ ϕ ( x 2 , y ) + δ \begin{aligned} \hat{w} \cdot \phi\left(x^{1}, \hat{y}^{1}\right) & \geq \hat{w} \cdot \phi\left(x^{1}, y\right)+\delta \\ \hat{w} \cdot \phi\left(x^{2}, \hat{y}^{2}\right) & \geq \hat{w} \cdot \phi\left(x^{2}, y\right)+\delta \end{aligned} w^⋅ϕ(x1,y^1)w^⋅ϕ(x2,y^2)≥w^⋅ϕ(x1,y)+δ≥w^⋅ϕ(x2,y)+δ

其中,红色代表正确的特征点(feature point),蓝色代表错误的特征点(feature point),可分性可以理解为,我们需要找到一个权值向量,其作用是与 ϕ ( x , y ) ϕ(x, y) ϕ(x,y) 做内积(inner product) ,能够将正确的point比蓝色的point的值均大于一个 δ δ δ。
结构化感知机
-
输出: w w w
-
算法

在可分情形下,为了得到 w ^ \hat{w} w^,我们最多只需更新 ( R / δ ) 2 (R / \delta)^{2} (R/δ)2次。其中, δ δ δ为间隔(使得误分的点和正确的点能够线性分离), R R R为 ϕ ( x , y ) ϕ(x, y) ϕ(x,y) 与 ϕ ( x , y ′ ) ϕ(x, y′) ϕ(x,y′)的最大距离(即特征之间最大的距离),与 y y y的空间无关!
不可分情形
考虑误差
正则化
结构化支持向量机




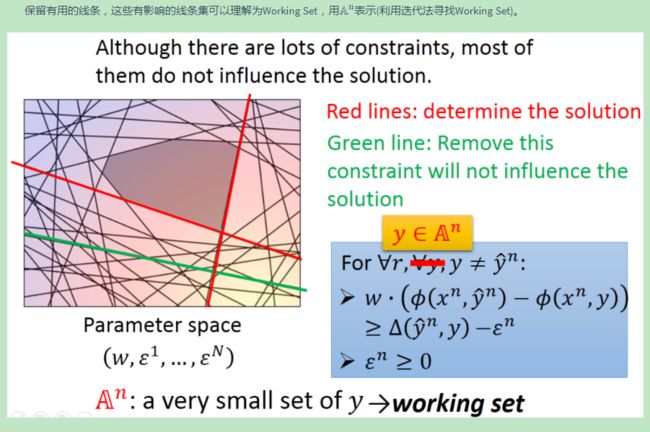
存在的问题:我们可能找不到一个 w w w满足以上所有的不等式都成立!
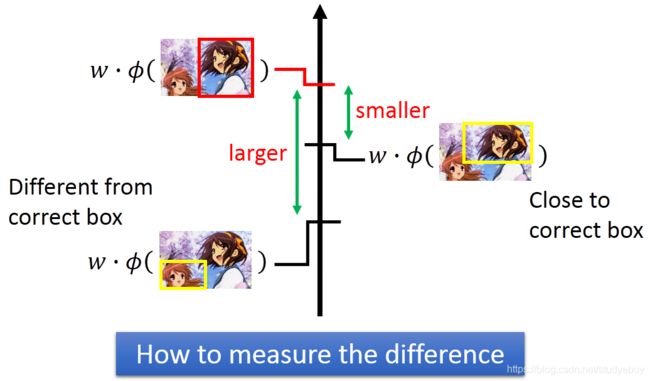
将margine(可以理解为正确的标框与错误的标框之间的一个差值,该差值越小,则margine越小,用 Δ \Delta Δ表示)减去一个 ε ε ε(即为了放宽约束 or 限制,使得margine变小,但限制不应过宽,否则会失去意义, ε ε ε越小越好,且要大于等于0)



结构化支持向量机:切割平面算法

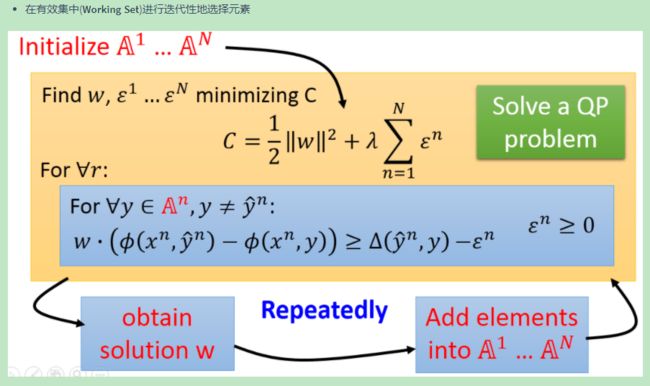









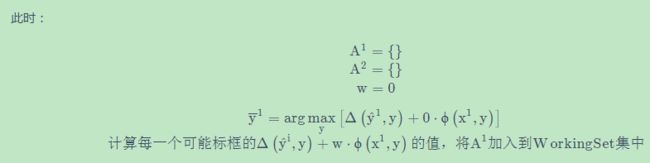




多类别支持向量机




二元支持向量机

深度神经网络和支持向量机
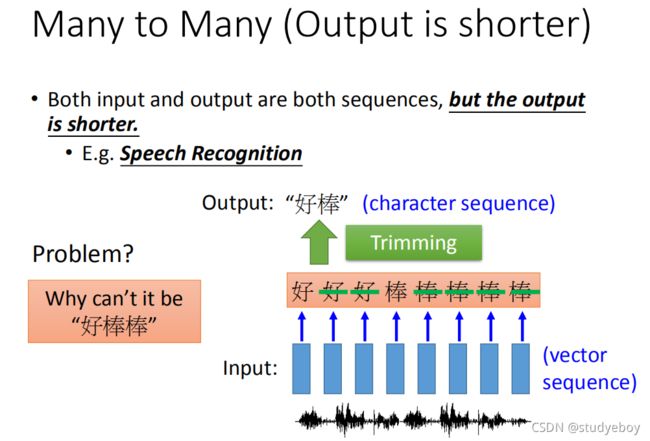
序列标注

序列标注的问题可以理解为:机器所要寻找的目标函数的输入是一个序列,输出也为一个序列,并且假设忽然输出的序列长度相同,即输入可以写成序列向量的形式,输出也为序列向量。该任务可以利用循环神经网络来解决,也可以基于结构化学习的其它方法进行解决(两步骤,三问题)。
隐马尔可夫模型(Hidden Markov Model,HMM)
隐马尔可夫模型有两步:第一步是基于语法生成一个合法的词性序列(generate a POS sequence based on the grammar);第二步是基于字典在第一步生成的词性序列的基础上生成一个句子序列(generate a sentence based on the POS sequence based on a dictionary)。
- 生成POS序列(基于语法)

假设大脑中有一个马尔科夫链,开始说第一句话时,放在句首的词性有50%的可能性为冠词,40%的可能性为专有名词,10%的可能性为动词,然后进行随机采样,再从专有名词开始,有80%的可能性后面为动词,动词后面有25%的可能性为冠词,冠词后面有95%的可能性Wie名词,名词后面有10%的可能性句子就结束了。用概率的形式表示为:P(“PN V D N”)=0.4x0.8x0.25x0.95x0.1。 - 根据词序生成一个句子(基于词典)
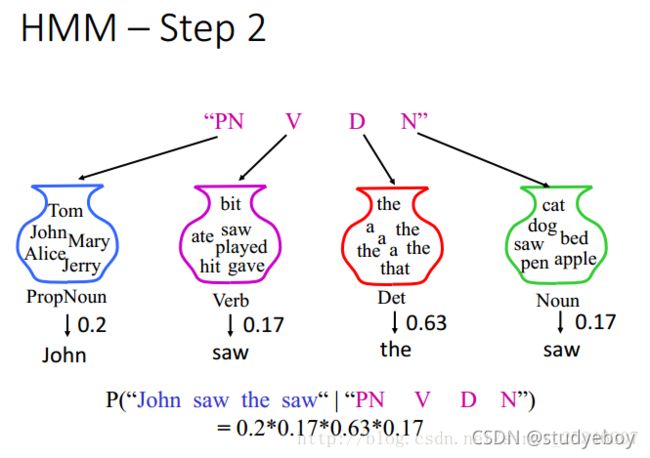
根据词性找到词典中对应的词汇,从不同的词性集合中采样出不同词汇所出现的几率,即P(“John saw the saw”|“PN V D N”)=0.2x0.17x0.63x0.17。
这两步之后就可以计算出x和y,对应的词性和句子一起出现的概率。

HMM可以描述为利用POS标记序列得到对应句子的几率。
将其一般化,可将第一步的概率称为转移概率(transition probability),第二步的概率称为输出概率(emission probability)。其概率值都可以通过训练数据得到。

隐马尔科夫模型的一般性解释:

计算概率值可以通过在训练数据中出现的次数计算得到。


词性标注的任务是给定x(句子序列),找到y(词性序列)。


需要遍历所有的y来找到能够使得P(x,y)最大的y,可以使用维特比算法(Viterbi Algorithm)减少计算的复杂度。


总结下HMM,至此其三个问题就得到了解决。


缺点
- HMM只依赖于每一个状态和它对应的观察对象。
计算转移概率和输出概率是分开计算的,认为其是相互独立的。然而序列标注问题不仅和单个词相关,而且和观察序列的长度,单词的上下文等相关。 - 目标函数和预测目标函数不匹配。
HMM学到的是状态和观察序列的联合分布P(Y,X),而预测问题中,需要的是条件概率P(Y|X)。 - 条件随机场(Conditional Random Field,CRF)

条件随机场(Conditional Random Field,CRF)
条件随机场对隐马尔科夫模型进行了改进。CRF假设概率P(x,y)正比于一个函数。


公式由来:




所以可以认为概率值是正比于一个权值和特征向量的内积。特征向量由两部分组成,一部分是标签和词的关系(relations between tags and words);

第二部分是标签之间的关系(relations between tags);

CRF的训练准则是找到满足的权值向量能够最大化目标函数。能够最大化我们所观察到 同时,最小化我们没有观察到的。


可以使用梯度上升(gradient ascent)方法来求解。

在求得权值向量和特征向量后,同样可以和隐马尔科夫模型一样使用维特比算法找到y。

训练
隐马尔可夫模型对比条件随机场
CRF没有HMM那样严格的独立性假设条件,因而可以容纳任意的上下文信息。CRF模型解决了标注偏置问题,去除了HMM中两个不合理的假设,当然,模型相应也变复杂 了。因此训练代价大、复杂度高。
生成模型or判别式模型(假设o是观察值,m是模型)
- 生成式模型:无穷样本->概率密度模型=产生式模型->预测
如果对P(o|m)建模,就是生成式模型,其基本思想是首先建立样本的概率密度模型,再利用模型进行推理预测。要求已知样本无穷或尽可能的大限制。这种方法一般建立在统计力学和Bayes理论的基础之上。HMM模型对转移概率和表现概率直接建模,统计共同出现的概率,是一种生成式模型。 - 判别式模型:有限样本->判别函数=判别式模型->预测
如果对条件概率P(m|o)建模,就是判别模型。其基本思想是在有限条件下建立判别函数,不考虑样本的产生模型,直接研究预测模型。代表性理论为统计学习理论。CRF是一种判别式模型。MEMM不是一种生成式模型,它是一种基于下状态分类的有限状态模型。
结构化感知机
结构化感知机与条件随机场
结构化支持向量机
HMM/CRF/Perceptron/SVM不同方法的性能比较
- 当训练数据更少的情况下,隐马尔可夫模型表现更好,其它方法性能不佳;
- 一般来说,条件随机场与结构化感知机没有明显的优劣之分,条件随机场为软类型的,而结构化感知机为硬类型的,结构化感知机只需要求解Q2就可以了,而条件随机场需要求解所有可能的情况;
- 结构化支持向量机整体表现最好;
- 命名实体识别类似于POS词性标记:结构化支持向量机模型表现最好,隐马尔科夫模型表现最差。
循环神经网络和 HMM/CRF/Perceptron/SVM比较
- 循环神经网络与长短时记忆网络
- 单方向的循环神经网络或长短时记忆网络并没有考虑到全部的序列,只考虑时间t1至当前时间tk的情形,对tk+1的情形没有考虑,即在时间tk时就已经有了输出结果。
- 成本函数和误差函数并不总数相关的。
- 可以叠加很多层(利用Deep的特性)。
- 隐马尔科夫模型、条件随机场、结构化支持向量机
- 在输出结果之前,做的都是利用维特比算法穷举所有的序列,观测最大的序列,在计算过程中考虑到的是整个序列;
- 可以明确的考虑输出标签之间的依赖关系;
- 结构化支持向量机的成本函数就是误差的上界,当成本函数不断减小的时候,误差就会随之降低。
所以,可以根据具体情况,选择使用单独的方法还是多种方法的融合方法。
- 深层方案
循环神经网络与长短时记忆网络 - 浅层方案
隐马尔科夫模型、条件随机场与结构化支持向量机 - 语音识别
卷积神经网络/循环神经网络或长短时记忆网络/深度神经网络+隐马尔科夫模型

- 语义标注
双向循环神经网络/长短时记忆网络+条件随机场/结构化支持向量机

模型总结
- 隐马尔可夫模型,条件随机场,结构化感知机或支持向量机都是求解三个问题;
- 三个方法定义评估函数的方式都有所差异;
- 结构化感知机或支持向量机跟几率都没有关系;
- 以上这些方法都可以加上深度学习让它们的性能表现的更好。
循环神经网络
1-of-N encoding方法将每一个单词表示成一个向量。

其它的改进版本

对于neural network来说,input一样的东西,output就应该是一样的东西,如果让neural network有记忆功能,它就可以解决input不同的词汇,output不同的问题。有记忆的neural network就叫作Recurrent Neural network(RNN),在RNN里面,每一次hidden layer的neuron产生的output的时候,这个output会被存到memory中,然后将记忆也作为网络的一个输入。

当然也可以将网络的输出存储在记忆中。
![]()
如果将隐藏层的输出存储在记忆中称为Elman Network,将输出层的输出值存储在记忆中就称为Jordan Network。Elman Network没有target,很难控制它学到什么hidden layer information,但是Jordan Network是有target的,可以比较清楚知道放在memory里面的是什么样的东西。
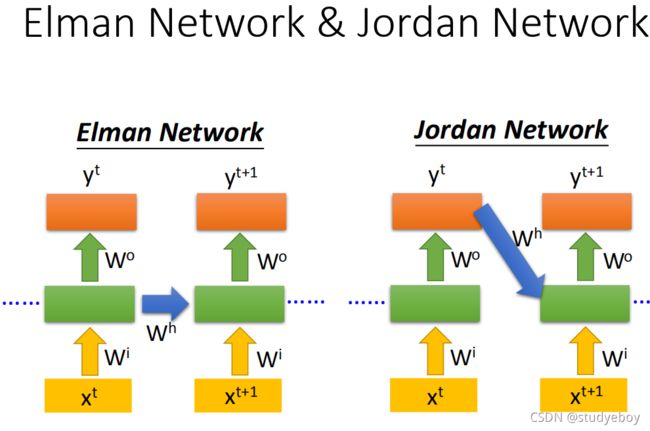
循环神经网络还可以是双向的,正向网络的输入和逆向网络的输入,都丢到输出层产生结果。双向网络在产生结果的时候,已经看到整个输入的序列,这样会比看到序列的一部分效果更好。
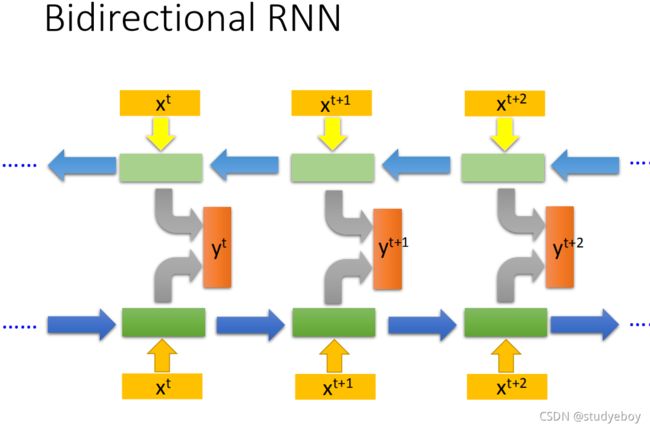
Recurrent Neural Network,它的memory在每一个时间点都会被洗掉,只要有新的input进来,每个时间点都会把memory洗掉,所以memory的Short-term是非常short的,但是Long Short-term Memory会较久一点,只要forget gate不决定忘记,它的值就会被存起来。Long Short-term memory(长时间的短期记忆),简称LSTM,具有多个长的短时间记忆网络。
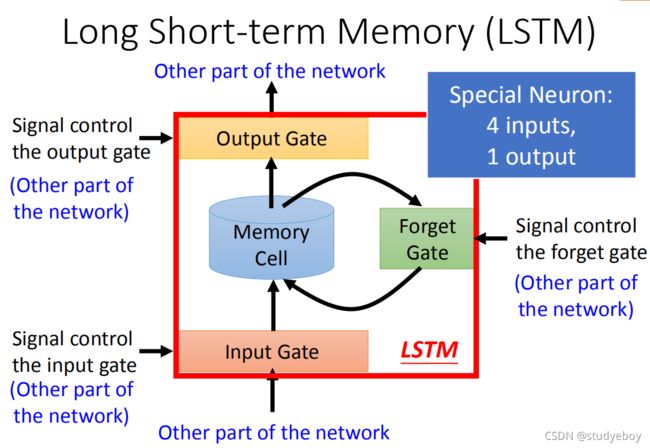
Long Short-term Memory有三个gate,当外界某个neural的output想要被写入memory cell的时候,必须通过一个input gate,input gate被打开的时候,才能把值写到memory cell里面,关起来的话,没有办法把值写进去。并且input gate的开关是neural network自己学习到的。对应的输出的dif也有一个output gate,output gate打开的时候,外接其他的neural可以从这个memory里面的值读出来,跟input gate一样,什么时候打开,neural network自己学习。第三个gate叫forget gate,决定什么时候memory cell要把过去记得的东西忘掉,也是network自己学习到的。
GRU是LSTM稍微简化的版本,它只有两个gate,虽然少了一个gate,但是performance跟LSTM差不多(少了1/3的参数,也是比较不容易overfitting)。如果你要用这堂课最开始讲的那种RNN,你要说是simple RNN才行。
LSRM举例:
network里面有一个LSTM的cell,input是三维的vector,output是一维的,假设input的第二个dimension x 2 x_2 x2的值是1时, x 1 x_1 x1的值就会被写到memory中,假设 x 2 x_2 x2的值是-1时,就会reset the memory,假设 x 3 x_3 x3的值为1时,就会把output打开看到输出。

假设原来存到memory里面的值是0,当第二个dimension x 2 x_2 x2的值是1时,3会被存到memory里面去。第四个dimension的 x 2 x_2 x2等于1,所以4会被存到memory里面去,所以会得到7。第六个dimension的 x 3 x_3 x3等于1,这时候7会被输出。第七个dimension的 x 2 x_2 x2的值为-1,memory里面的值会被洗掉变为0。第八个dimension的 x 2 x_2 x2值为1,所以把6存进去,因为 x 3 x_3 x3的值为1,所以把6输出。
LSTM运算举例:
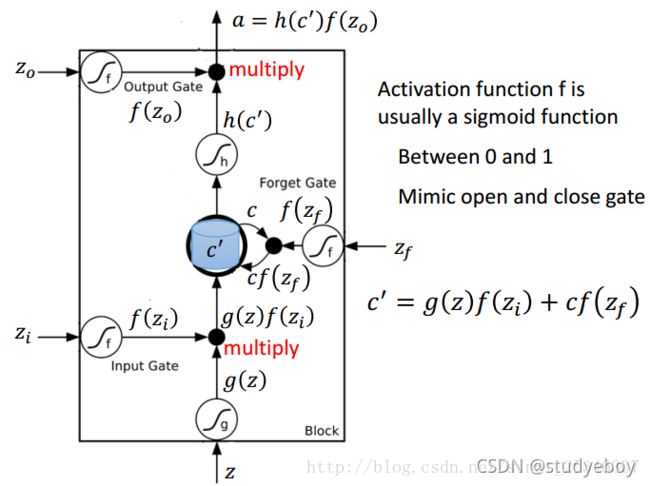
下面图中是一个memory cell,四个input scalar:input的三维vector乘以linear transform以后所得到的结果( x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3乘以权重再加上bias),这些权重和bias是通过train data用GD学到的,用这样的 输入会得到怎样的输出?
首先,根据input,分析可能会得到的结果,底下是外界传入的cell, x 1 x_1 x1乘以1,其它的vector乘以0,所以就直接把 x 1 x_1 x1当作输入。在input gate时, x 2 x_2 x2乘以100,bias乘以-10,假设 x 2 x_2 x2是零值的话,通常input gate是关闭的,bias等于-10,因为-10通过sigmoid函数之后会接近0,所以就代表是关闭的,若 x 2 x_2 x2的值大于1的话,结果会是一个正值,代表input gate会被打开。forget gate通常会被打开的,因为它的bias等于10,只有当 x 2 x_2 x2的值为一个很大的负值时,才会把forget gate关闭。output通常是被关闭的,因为bias是一个很大的负值,若 x 3 x_3 x3有一个很大的正值,大于bias则把output打开。

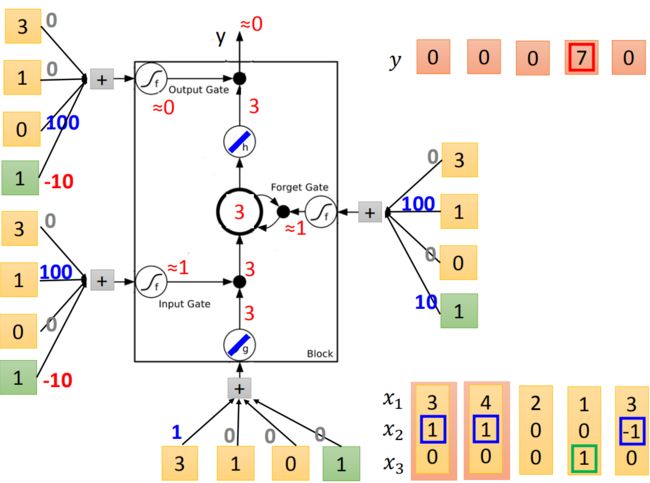

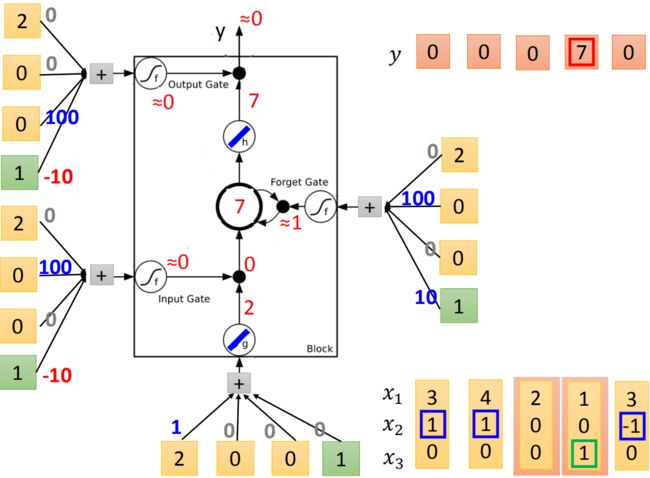
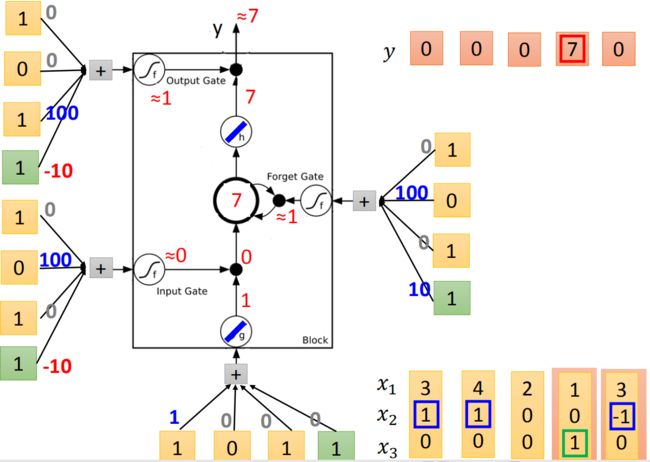

假设g和h都是linear,存到memory里面的初始值是0,input第一个vector(3,1,0),input: 3 × 1 = 3 3\times1=3 3×1=3,输入的值为3。input gate: 1 × 100 − 10 ≈ 1 1\times 100-10 \approx 1 1×100−10≈1,是被打开的。 g ( z ) ∗ f ( z i ) = 3 g(z)*f(z_i)=3 g(z)∗f(zi)=3。forget gate: 1 × 100 + 10 ≈ 1 1\times100+10 \approx 1 1×100+10≈1是被打开的。现在KaTeX parse error: Expected group after '^' at position 2: c^̲' = g(z)f(z_i)+…存到memory里面的是3。output gate: 1 × 100 − 10 ≈ 1 1\times100 - 10 \approx 1 1×100−10≈1是被关起来的,所以3无法通过,所以输出值为0。
接下来input(4,1,0),传入input的值为4,input gate会被打开,forget gate也会被打开,所以memory里面存的值等于7(3+4=7),output gate仍然会被关闭的,所以7没有办法被输出,所以整个memory的输出为0。
接下来input(2,0,0),传入input的值为2,input gate关闭(\approx≈ 0),input被input gate给挡住了(0 *2=0),forget gate打开(10)。原来memory里面的值还是7(1 *7+0=7).output gate仍然为0,所以没有办法输出,所以整个output还是0。
接下来input(1,0,1),传入input的值为1,input gate是关闭的,forget gate是打开的,memory里面存的值不变,output gate被打开,整个output为7(memory里面存的7会被读取出来)
最后input(3,-1,0),传入input的值为3,input gate 关闭,forget gate关闭,memory里面的值会被洗掉变为0,output gate关闭,所以整个output为0。
LSTM原理:
原来的neural network里面有很多neural,会把input乘以不同的weight当作不同的neural输入,每一个neural都是一个function,输入一个值然后输出一个值。LSTM把memory的cell当成一个neural。所以LSTM是有四个input跟一个output,需要四个input才能产生一个output,所以LSTM需要的参数量是一般neural network的四倍。



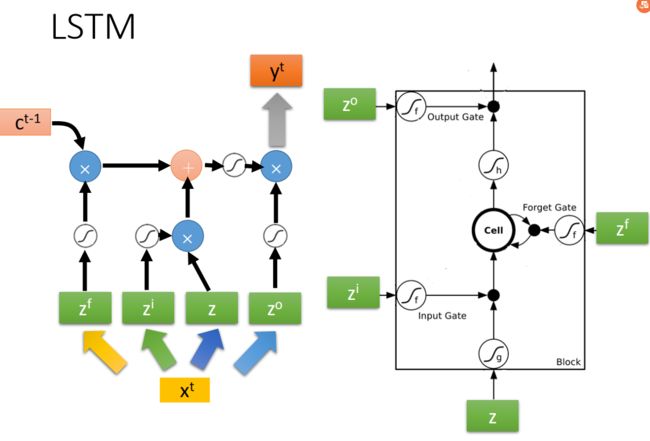

在学习训练RNN时可以用梯度下降方法。

但是基于RNN的网络是不好训练的,损失曲面要不是平的要不就是陡峭的,不易训练。

通过LSTM可以很好的解决此问题,因为LSTM与普通RNN不同的是,LSTM的记忆和输入是相加的,而不是直接清零的。除非forget gate关闭时,影响才会消失。因此只要确保大多数情况下forget gate是开启的,就可以解决梯度消失(gradient vanishing)的问题,不是梯度爆炸(gradient exploding)。

循环神经网络的应用场景:
集成学习
Ensemble是一种团队合作方法,组合多个模型,以获得更好的效果,使集成的模型具有更强的泛化能力。其主要方法有Bagging(Random Forest)、Boosting(AdaBoost&Gradient Boost)和Stacking。
Bagging
Bagging的主要思想是让很容易overfitting的模型变得不那么overfitting,该方法适用于复杂的、容易过拟合的模型。通过有放回的取样的方法将训练样本分为不同的训练集,并训练出不同的模型,通过这所有的模型的输出做投票或者平均来作为最终的输出结果。

上图表示了用自己采样的数据进行Bagging的过程,在原来的N笔数据中进行采样,过程就是每次从N笔训练数据中取N’(通常N=N’)建立很多个dataset,这个过程抽取到的可能会有重复的数据,但是每次抽取的是随机形成的dataset。每个dataset都有N’笔data,但是每个dataset的数据都是不一样的,用一个复杂的模型对四个dataset都进行学习得到四个function,在testing的时候,把testing data放到这四个function里面,把得出来的结果做平均(回归)或者投票(分类),通常来说表现(variance比较小)都比之前的好,这样就不容易产生过拟合。做Bagging的情况:模型较复杂,容易产生过拟合。(容易产生过拟合的模型:决策树)目的:降低方差。
随机森林(Random Forest)就是决策树(Decision Tree)做Bagging的版本。假设给定的每个Object有两个feature,用这个training data建立一棵树,如果x1小于0.5就是yes(往左边走),当x1大于0.5就是no(往右边走),接下来看x2,当x2小于0.3时就是class1(对应坐标轴图中左下角的蓝色),当大于0.3时就是class2(红色);对右边的当x2小于0.7时就是红色,当x2大于0.7就是蓝色。

随机森林(Random Forest),指的是利用多棵树对样本进行训练并预测的一种分类器,其输出结果是由个别树输出的类别的众数而定。
随机森林不仅对训练数据进行了重采样,并且对于每棵树,都随机的有限制特征或问题,以此来避免树长得太像。测试时用的数据就可以是训练时没有用到的数据,再将其做OOB误差作为模型最终效果。

假设有training data是 x 1 , x 2 , x 3 , x 4 x^1, x^2, x^3, x^4 x1,x2,x3,x4, f 1 f_1 f1只用第一笔和第二笔data训练(圆圈表示训练,叉表示没训练), f 2 f_2 f2只用第三笔和第四笔data训练, f 3 f_3 f3用第一、第三笔data训练, f 4 f_4 f4表示用第二、第四笔data训练,在训练 f 2 f_2 f2和 f 4 f_4 f4的时候都没有用到 x 1 x^1 x1,所以可以用 f 2 f_2 f2和 f 4 f_4 f4的Bagging的结果在 x 1 x^1 x1上测试他们的表现,同理,可以用 f 2 f_2 f2和 f 3 f_3 f3的Bagging的结果来测试 x 2 x^2 x2,下面几个也是同样的道理。最后把每个测试的结果取平均的error,就作为最后 error。
Boosting
Boosting的主要思想是提升那些弱的分类器(分类效果比乱猜好一点就行,准确率高于50%)。

Boosting是用在很弱的模型上的,当我们又很弱的模型的时候,不能fit我们的data的时候,就可以用Boosting的方法。Boosting有一个很强的保证:如果机器学习算法能产生错误率小于50%的分类器,这个方法可以保证错误率达到0%。Boosting的结构:
- 首先找到一个分类器 f 1 ( x ) f_1(x) f1(x)
- 再找一个辅助 f 1 ( x ) f_1(x) f1(x)的分类器 f 2 ( x ) f_2(x) f2(x)(注意: f 2 ( x ) f_2(x) f2(x)如果和 f 1 ( x ) f_1(x) f1(x)很像,那么 f 2 ( x ) f_2(x) f2(x)的帮助效果就不好,所以需要尽量找互补的 f 2 ( x ) f_2(x) f2(x),能够弥补 f 1 ( x ) f_1(x) f1(x)没办法做到的事情)
- 得到第二个分类器 f 2 ( x ) f_2(x) f2(x)
- 结合所有的分类器得到结果(注意:Boosting的训练是有顺序的sequentially,Bagging是没有顺序的,可以同时train)
如何得到不同的分类器
AdaBoost
先训练一个分类器 f 1 ( x ) f_1(x) f1(x),要找一组新的training data,让 f 1 ( x ) f_1(x) f1(x)在这组data上的表现很差,然后让 f 2 ( x ) f_2(x) f2(x)在这组training data上训练。




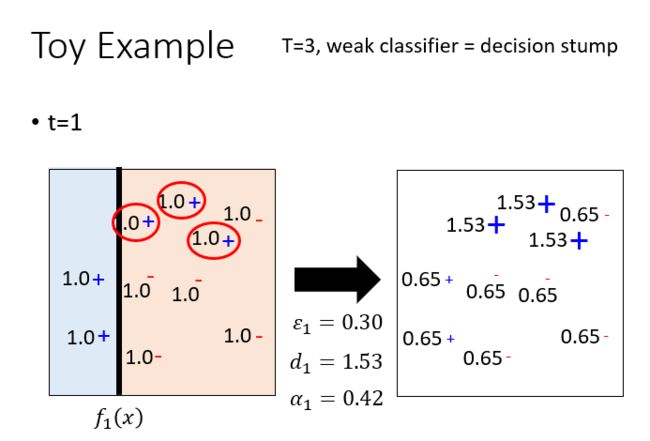


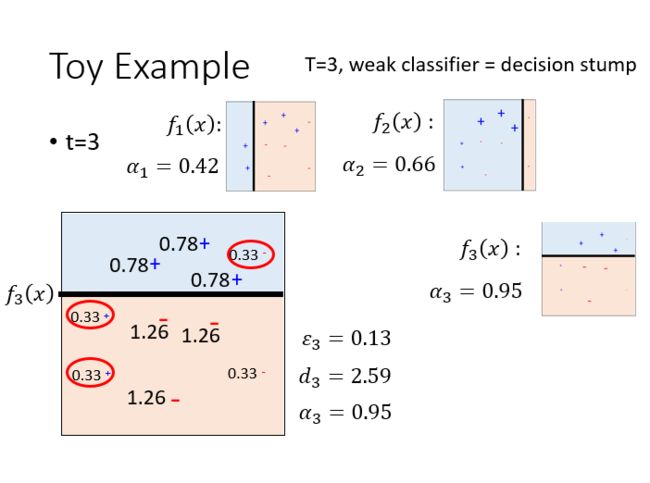
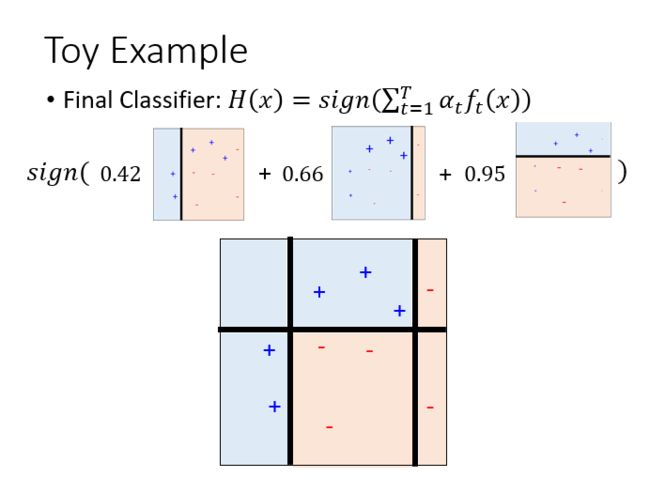
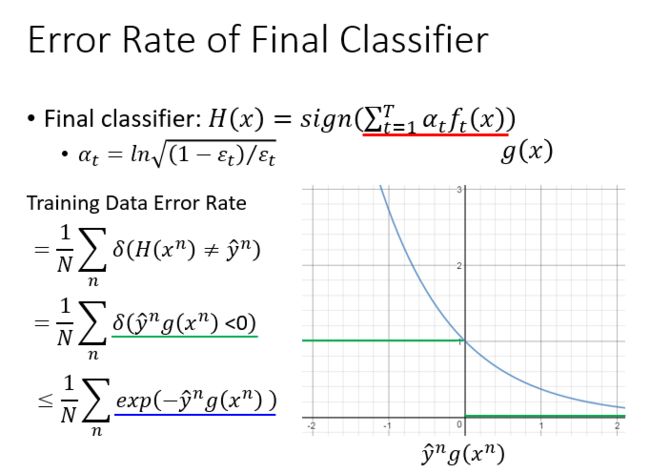
AdaBoost证明推导:



Gradient Boosting
Gradient Boosting是Boosting的更泛化的一个版本。




Gradient Boosting和AdaBoost不同,Gradient Boosting在迭代的时候选择梯度下降的方向来保证最后的结果最好。损失函数用来描述模型的“靠谱”程度,假设模型没有过拟合,损失函数越大,模型的错误率越高。如果模型能够让损失函数持续的下降,则说明模型在不停的改进,而最好的方式就是让损失函数在其梯度方向上下降。
Stacking
Stacking的思想是用每个模型的输出生成一个新的特征,在一个最终分类器上做分类得到最终结果。训练数据要分成两份,一份来训练出多个模型,另一份用来训练最终的分类器。

深度强化学习(Deep Reinforcement Learning)
Deep Reinforcement Learning:AI=RL+DL。增强学习(Reinforcement Learning,RL)又叫强化学习,是近年来机器学习和智能控制领域的主要方法之一。增强学习关注 是智能体如何在环境中采取一系列行为,从而获得最大的累积回报。通过增强学习,一个智能体应该知道在什么状态下应该采取什么行为,RL是从环境状态到动作映射的学习,这个映射称为策略。
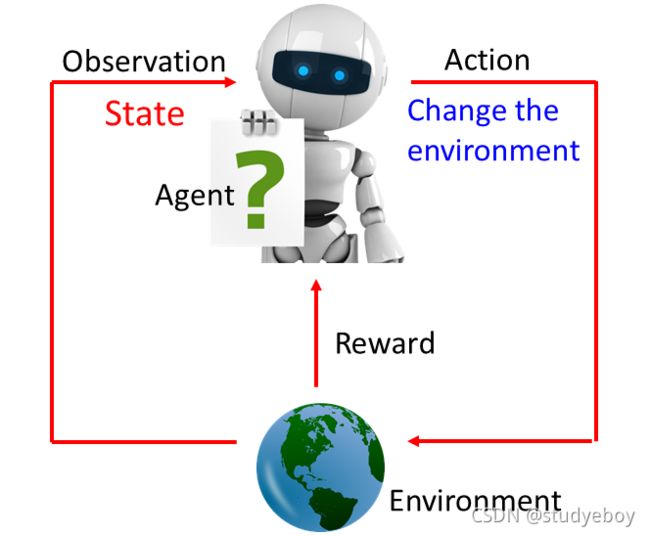
增强学习和监督学习:
- 增强学习是试错学习,由于没有直接的指导信息,智能体要以不断与环境进行交互,通过试错的方式来获得最佳策略。
- 延迟回报,增强学习的指导信息很少,而且往往是在事后(最后一个状态)才给出的,这就导致了一个问题,就是获得正回报或者负回报后,如何将回报分配给前面的状态。

强化学习的应用:
![]()
强化学习的方法:
Reinforcement Learning的方法分成两大块,一个是Policy-based的方法,另一个是Valued-based的方法。先有Valued-based方法,再有Policy-based方法。在Policy-based的方法里面,会learn一个负责做事的Actor,在Valued-based的方法会learn一个不做事的Critic,专门批评不做事的人。把Actor和Critic加起来叫作Actor+Critic的方法。
Policy-based方法
Machine Learning就是找一个Function,Reinforcement Learning也是Machine Learning的一种,所以要做的事情也是要找Function。Actor就是 Function,这个Function的input是Machine看到的observation,它的output是Machine要采取的Action。通过reward来找这个best Function。

找best Function的三个步骤:



Valued-based 方法
A critic 不会决定行为,给定一个actor,它评估actor的好坏,A critic是一个它评价的actor函数,函数是由神经网络表示的。
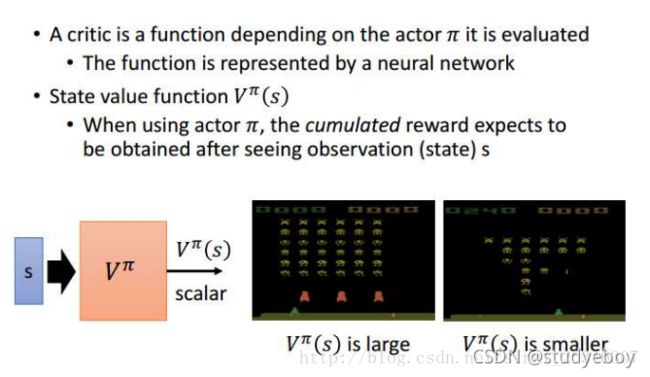
有三种类型的critics:
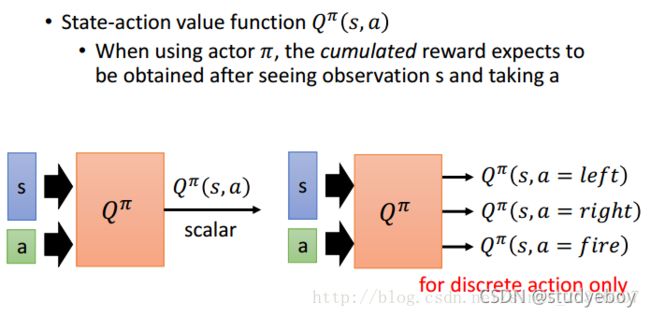

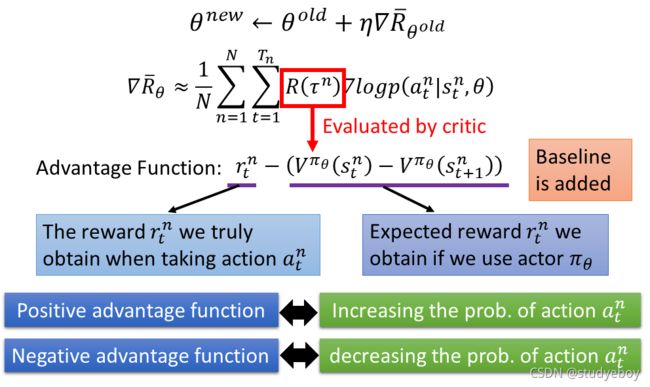
Actor-Critic
参考资料
李宏毅机器学习2016 第二十一讲 隐马尔可夫模型和条件随机场
机器学习Hung-yi Lee 2016