2021 神经网络压缩 （李宏毅

首先，为什么需要对神经网络模型进行压缩呢？我们在之前的课程中介绍过很多大型的深度学习模型，但当我们想要将这些大模型放在算力比较小的边缘设备或者其他IoT设备里面，就需要对大模型进行压缩。

Lower latency：低时延 Privacy：私密性

介绍5个网络压缩的方法，我们只考虑算法（软件）层面，不考虑硬件层面的解决方法。

 

1. Network Pruning（网络剪枝）

对于一个大的网络来说，我们能想到的是，众多网络参数中一定会有不重要/冗余的一些参数，因此我们将这些参数减掉达到网络压缩的目的。

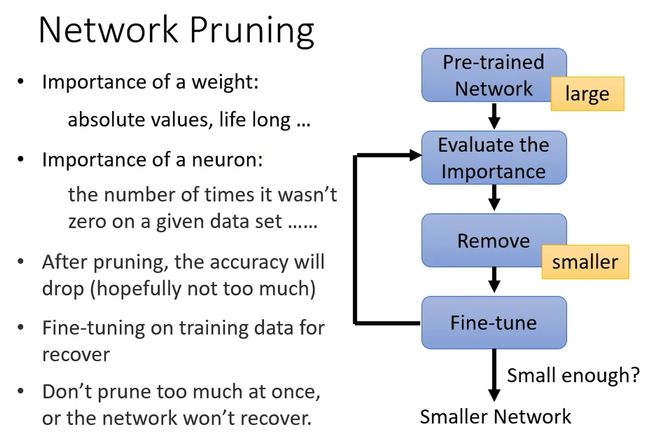
网络剪枝的步骤如下：首先，我们预训练一个大规模的网络，然后评估里面参数的重要性，包括权重（weight）的重要性和神经元（neuron）的重要性。

• 评价weight重要性，我们可以用绝对值衡量，即绝对值越大，weight越重要，或者采用之前介绍的life long learning的想法（也許我們也可以就把每個參數的 bi 算出來、就可以知道那個參數重不重要）。
• 评价neuron重要性，我们可以用其输出的结果为0的次数衡量，即输出0越多越不重要。

接着我们对多余的参数的重要性评估并修剪，得到一个小的网络，再对里面的参数微调，再评估、修剪。。。重复上述过程，直到满足要求，完成Network pruning过程。（一次剪掉大量参数可能对network伤害太大，所以一次只剪掉一点参数比如10%）

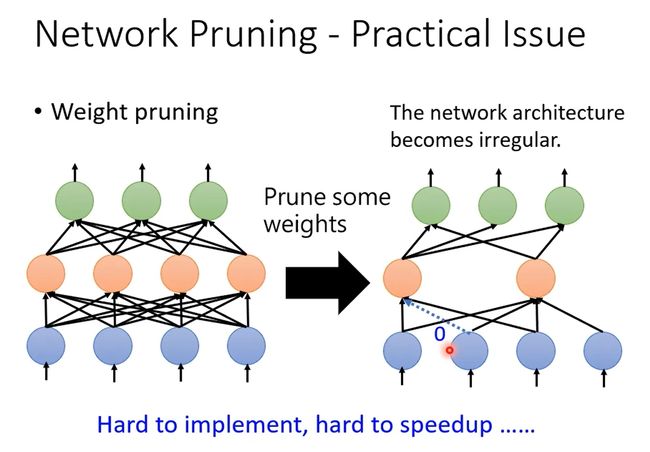
刚才提到，修剪的单位有两种，一种是以权重（weight）为单位，一种是以神经元（neuron）为单位，这两者有什么不同呢？实作上差别较大

首先Weight pruning，但这样就造成network 形状不规则（irregular），难以编程实现（pytorch定义network每一層有幾個 Neuron/ vector），同时难以用GPU加速(矩阵乘法)。通常的做法是将冗余的weight置为0，但这样做还是保留了参数（等于0），不是真正去除掉。

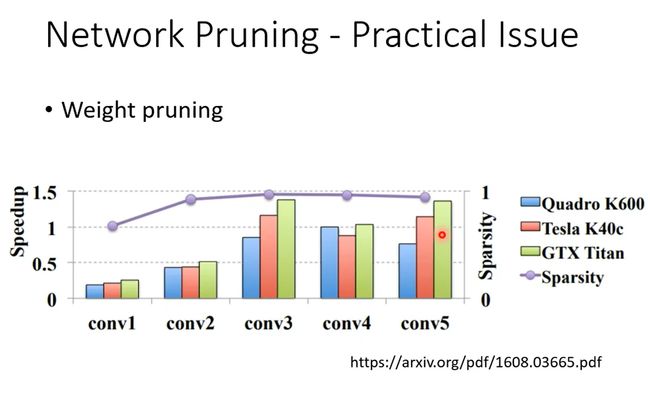
在这篇论文中有个关于参数pruning多少与训练速度提升关系的实验验证，其中紫色线sparsity表示参数去掉的量。可以发现，虽然参数去掉了将近95%，但是速度依然没有提升。

（這個 Network Pruning 的方法、其實是一個非常有效率的方法、往往你可以 Prune 到 95% 以上的參數、那但是你的 Accuracy 只掉 1~2% 而已）

接着Neuron pruning，通过去除冗余的神经元，简化网络结构。这样得到的网络结构是规则的，相比于Weight pruning，这种方式更好实现，也更容易通过GPU加速。

Q&A：這個 Pruning 有沒有效率是函式庫的問題？對啦 是函式庫的問題、那如果你可以想辦法寫一個、Irregular的 Network也很有效的函式庫的話、那你就可以用 Weight Pruning、但是 大家都沒有要自己寫函式庫

为什么我们先训练一个大的network，再压缩成一个小的network，而不是直接训练一个小的network呢？一般来说，大的network更容易训练，如果直接训练小的网络可能达不到大的network的训练效果。

why大的network比较好train？参看过去课程录影。这里有个大乐透假说（Lottery Ticket Hypothesis）对上述观点进行了说明。

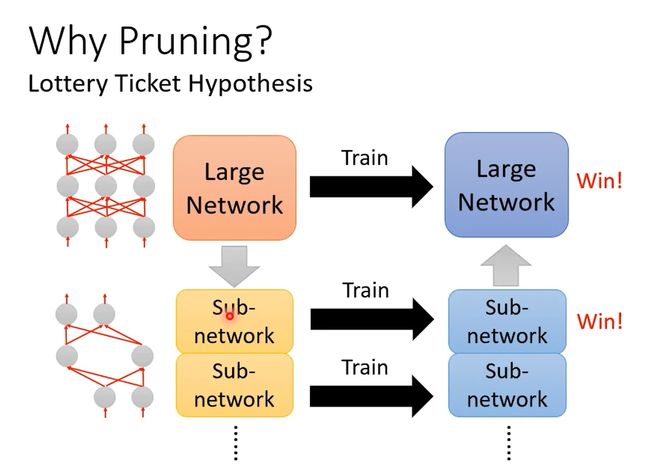
什么是大乐透假说（Lottery Ticket Hypothesis）呢？

train network是看人品的，每次 Train Network 的結果不一定會一樣，你抽到一組好的 Initial 的參數，就会得到好的结果。

现在有一个训练好的大的网络，可以分解成若干个小的网络，只要某一个小的网络性能与大的网络相同或相似，就说明这个大的网络可以压缩。

大乐透假说在实验上是怎么被证实的呢？

用大樂透假說來解釋上图的现象，就是大network裡面有很多 Sub-network、而這一組 Initialize 的參數，就是幸运的那一组、可以 Train 得起來的 Sub-network

大樂透假說非常知名，在ICLR2019得到 Best Paper Award

关于大乐透假说的一个后续的研究如下，“解构大乐透假说”，通过充分的实验得到了一些有趣的结论：

• 第一个发现是，尝试了不同的pruning strategy，发现如果训练前和训练后参数的差距越大，将其pruning后得到的结果越有效。
• 第二个发现是，到底我們今天這一組好的 Initialization好在哪里,   发现说 小的sub-network只要我们不改变参数的正负号，就可以训练起来。说明：正負號是初始化參數 能不能夠訓練起來的關鍵
• 第三个发现是，对于一个初始的大的网络（因为参数随机初始化很关键），有可能不训练就已经有一个sub-network可以有一个比较好的效果。（其实可以得到跟supervise很接近的正确率）

但是  大乐透假说一定是对的吗？不一定。下面这篇文章就“打脸”了大乐透假说。实验是这样的，我们用pruned完的小网络随机初始化参数，再训练，只要多训练几个epoch，就可以比不随机初始化训练小网络的效果要好。

当然这篇文章的作者也给出了一些对大乐透假说的回应，大乐透假说出现的前提是当learning rate很小，或者unstructured（做Weight pruning ）时候才有可能出现大乐透假说现象。

所以大乐透假说,  未來尚待更多的研究來證實

2. Knowledge Distillation

Knowledge Distillation的精神和 Network Pruning 其實也有一些類似的地方

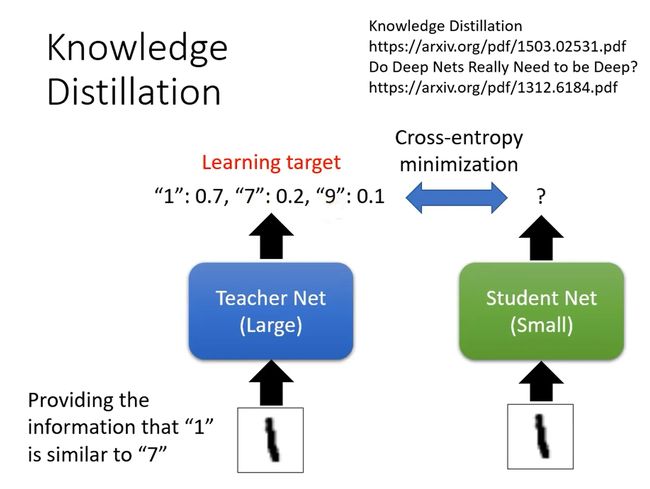
Knowledge Distillation做法如下：首先我们先train一个大网络，叫Teacher Net。student network是去根據這個 Teacher Network 來學習。学生 不是去看這個圖片的正確答案來學習、他把老师的输出 就當做正確答案。

这样做是因为：直接 Train 一個小的 Network 往往結果就是沒有從大的 Pruning 來得好

Knowledge Distillation其实不是新的技术，最知名的文章其实是Hinton在2015年就发表了，

Teacher Net其實會提供這個 Student Network 額外的資訊

那其實 Knowledge Distillation 有些神奇的地方、如果你看那個 Hinton 的 Paper 裡面、它甚至可以做到  光是 Teacher 告訴 Student 哪些數字之間、有什麼樣的關係這件事情、就可以讓 Student在完全沒有看到某些數字的訓練資料下、就可以把那一個數字學會

这个Teacher Net不一定是一个巨大的network，也有可能是将多个network组合（ensemble）得到的。

(ensemble是机器学习比赛里一个非常常用的技巧，你就訓練多個模型  然後你輸出的結果就是多個模型、投票的結果就結束了。或者是把多个模型的输出平均起来，

做个超级ensemble，训练个100 個模型啊1000個模型，把那麼多的模型的結果通通平均起來，往往你要在機器學習的 這種 Leaderboard 上面名列前茅，靠的就是这个技术，

network output上做平均，也可以在network参数上做平均  在translation作业里用过，这一招在translation上不知道为什么特别有用)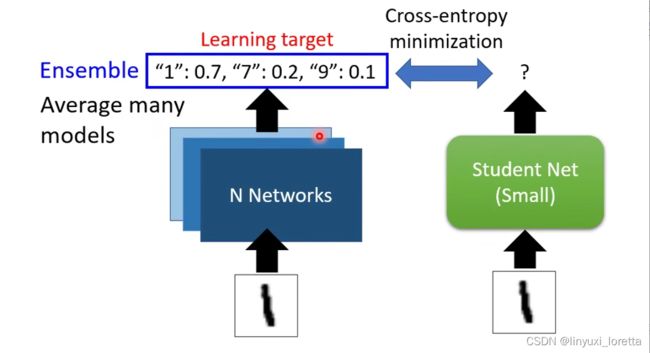

 关于Knowledge Distillation的一个小技巧，在softmax函数基础上对每个输出结果加一个超参数T（Temperature），这样会对最后的预测结果进行一个平滑处理，让Student Net更好训练一些。

(softmax就是，你把每一個 Neural 的輸出、都取 Exponential然后再做normalize得到最終 Network 的輸出)

还有人会拿network每一层都拿来train，比如大的有12层，小的6层，可以拿小的第6层像大的12层，小的第3层像大的第6层，往往做比较多的限制，可以得到更好的结果。

3. Parameter Quantization

Parameter Quantization参数量化，也可以称为参数压缩。用比较少的空间来储存一个参数，具体来说有如下几种方式：

1. 减少参数精度。对于Weight的精度可能不需要太高就可以获得一个比较好的效果，比如从64位调整为32位或者16位等等，这样就可以减少存储的数据量。
2. Weight clustering（权重聚类）：将神经网络所有weight按数值接近进行分群，数值差不多的聚成一类。分几群事先设定好。然后对每个类取一个值（可以是平均值）替换里面所有的权值，相当于每一堆只用一个值就可以存储，这样存储的数据量也大大减少。
3. 采用信号处理中常用的一种方法：Huffman encoding（哈夫曼编码），常出现的东西用比较少的bit描述，不常出现的东西用比较多的bit描述，这样平均起来存储的数据量将大大减少。

Q&A：Weight Clustering 要怎麼做 Update、每次 Update 都要重新分群嗎？

Weight Clustering其实有个简单做法是，network训练完后、再直接做 Weight Clustering

但直接做，可能会导致 Cluster 後的參數、跟原來的參數相差太大

所以 有一個做法是  我們在訓練的時候要求 Network 的參數 彼此之間比較接近、你可以把這個訓練的 Quantization 當做是Loss 的其中一個環節、直接塞到你的訓練的過程中。让训练中达到 参数有群聚的效果，

Q&A：每個 Cluster 的數字要怎麼決定呢？ 就是決定好每個 Cluster 的區間之後取平均。

weight到底可以压缩到什么程度呢？最终极的结果就是，每个weight只需要1bit就可以存下来,  网络中的weight要么是+1，要么是-1，像这样Binary Weights的研究还蛮多的，可以参考的reference如图：

那这样训练出的网络效果会不会不太好？这里有一篇文章是binary network里一个经典的方法Binary Connect，

介绍了该方法用于3种数据集的图像分类问题中，结果发现BinaryConnect的方法识别错误率更小，原文给出的解释是这种方法给network比较大的限制，会在一定程度上减少overfitting情况的发生。

4. Architecture Design（Depth Separable Convolution）

通过network架构的设计 来达到减少参数量的效果，

这里介绍一种关于CNN的减少参数量的结构化设计。

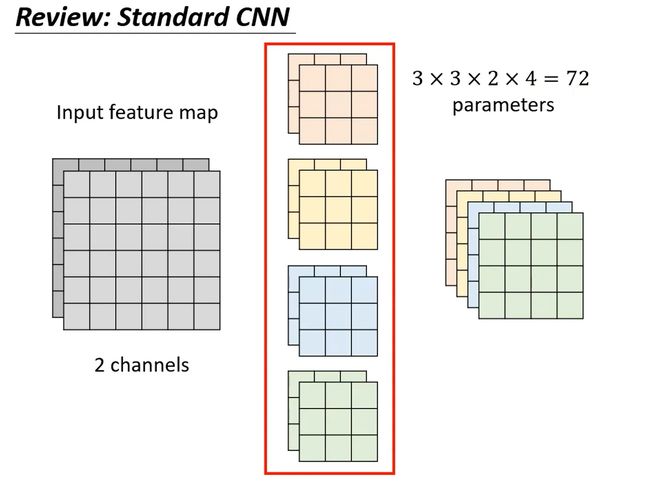
首先回顾一下CNN，在 CNN 的 Convolution Layer 裡、每一個 Layer 的 Input 是一個 Feature Map,  假设输入有2个channel，对应的filter也是2个channel。假设有4个filter，每个filter都是3*3的，那么输出就有4个channel。卷积层共有 3∗3∗2∗4=72 个参数。

接着介绍Depth Separable Convolution，它分为两个步骤：

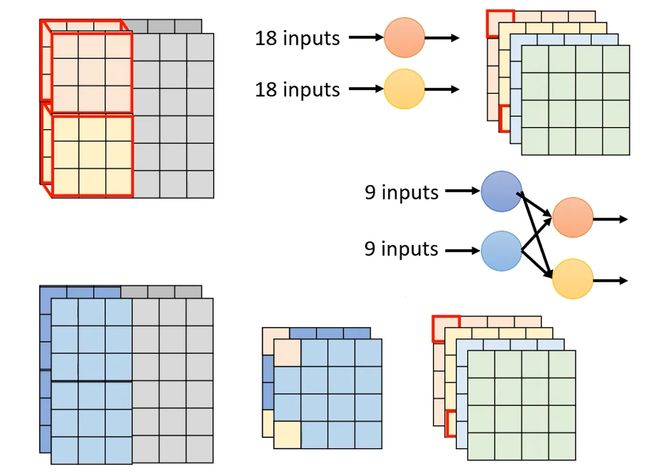
1. Depthwise Convolution

它在做卷积的时候与传统的对图像做卷积有很大的不同。图片有几个channel就对应有几个filter，每个filter只管一个channel。

但是只做Depthwise Convolution会遇到一个问题，channel和channel之间没有任何互动，假设某个pattern是跨channel才能看的出来，这种方法无能为力。

上述过程有 3∗3∗2=18 个参数。

2. Pointwise Convolution

为了解决无法学习输入图像channel与channel之间联系的问题，将Depthwise Convolution的输出结果用 1x1 的filter做卷积，以4个filter为例，效果如下：

上述过程有 2∗4=8 个参数。

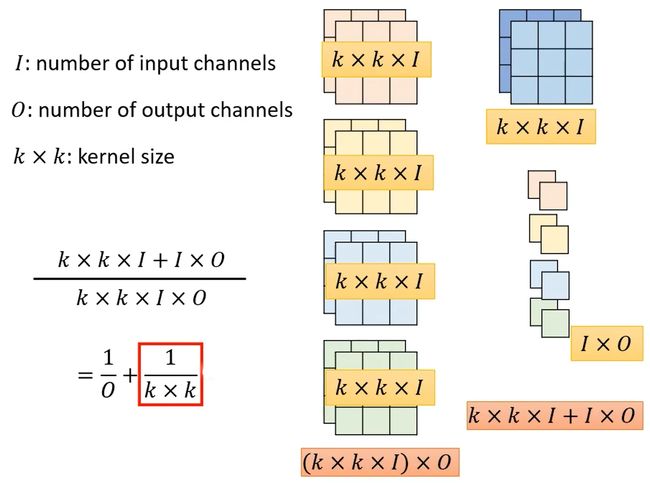
将标准CNN和Depth Separable Convolution参数量做对比，可以发现Depth Separable Convolution参数量比CNN要少很多。

那因為 O 通常是一個很大的值、你的 Channel 數目你可能開個 256 啊 512 啊。今天常用的 Kernel Size 可能是 3 x 3 或者是 2 x 2

上述方法为什么有效呢？

过去有一招Low rank approximation，來減少一層 Network 的參數量。如果神经网络某一层输入为N，输出为M（假设非常大），那么对应的weight就有 N∗M 个。这时，如果我们在N和M中间加一层，这一层不用激活函数，直接多插一层，neuron数目是K 。当K比较小时，参数量相比于 N∗M 会大大减少。比如N和M都是1000，K 可以塞個 20、50。但是这样的做法会减少W的可能性，本来W可以放任何参数，拆成这样W的rank ≤ K。

Depth Separable Convolution其实就是用了把 “1层拆成2层 ”这样的概念，相当于将CNN中间多加了一层，这样就可以减少整体网络的参数量。

关于网络结构设计方面还有一些文献参考，感兴趣可以看一下里面相关的内容，这里就不多介绍。

5. Dynamic Computation（动态计算）

在前幾個方法裡面想要做的事情、就是單純的把 Network 變小

而Dynamic Computation让network可以自适应调整计算量，比如让神经网络自适应不同算力的设备，或者同一设备不同电量时对算力的分配。

为什么不在一个设备上放好多个模型呢？因为需要占更多的空间。

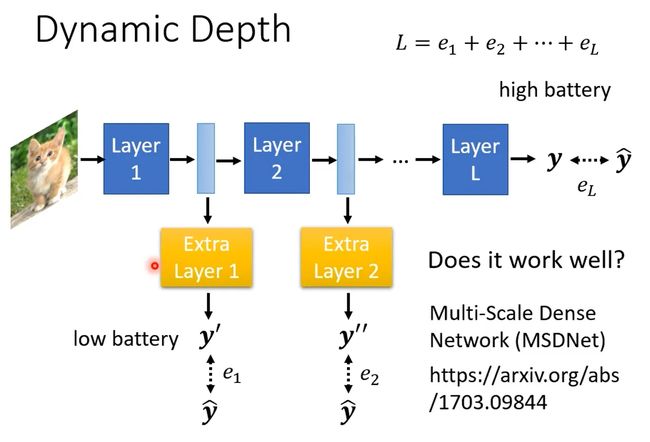
如何自适应调整网络的计算量？讓 Network 自由調整它的深度，

这种方式效果到底如何？可以用.. 比较好一点的方法（MSDNet）。

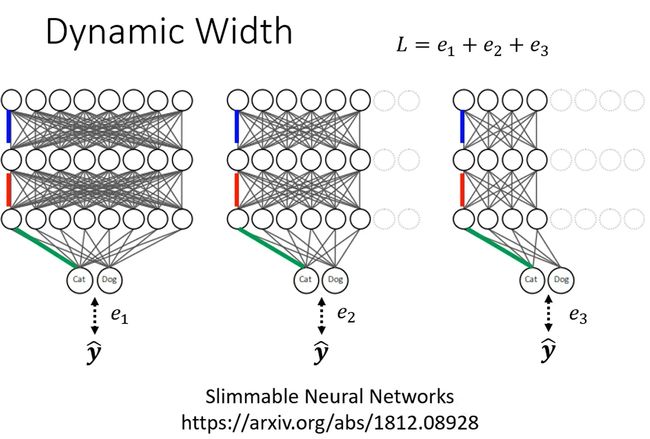
讓 Network 自由决定它的宽度，。

强调一下：是同一個 Network，可以選擇不同的寬度。标一样颜色的就是同一個 Weight

事先决定好 在只要用 75% 參數的時候，某一些neuron不要用到，

训练时 就把所有的狀況一起考慮、然後所有的狀況都得到一個 Output，

上述两种方法都是人为决定根据设备不同的算力（比如电量）动态调整网络深度和宽度，

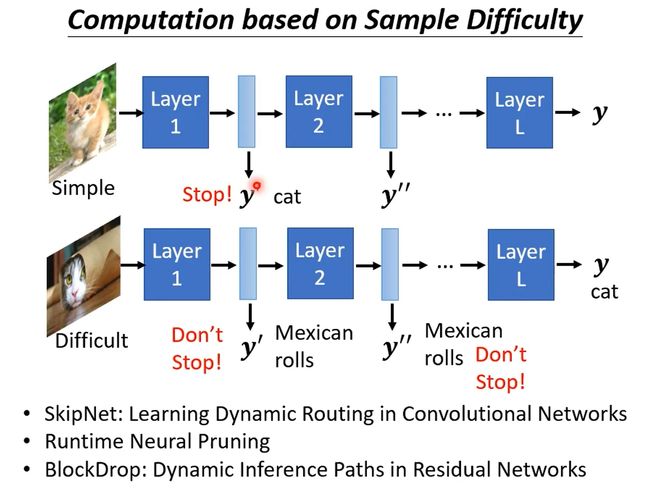
让network自行决定、根据情景 、決定它的寬度或者是深度。比如，对于不同难度的训练样本可能需要的层数也不一样。

最后总结一下，关于神经网络压缩（Network Compression）的这几种方法，它们并不是互斥的，可以先用某一个方法，再接着用剩余的一个或几个方法，直到满足压缩条件。