【机器学习】线性回归【上】朴素最小二乘估计

主要参考了B站UP主“shuhuai008”和“王木头学科学”，以及DeepLearning（花书/圣经），包含自己的理解。
有任何的书写错误、排版错误、概念错误等，希望大家包含指正。

由于字数限制，分成两篇博客。
【机器学习】线性回归【上】朴素最小二乘估计
【机器学习】线性回归【下】正则化最小二乘估计

提醒 下文中的 $\alpha$ 和 $\lambda$ 在不同的小章节中可能表示不同的含义，一般地，$\alpha$ 表示向量或正则化，$\lambda$ 表示学习率或特征值（向量）等。

规定符号。

数据集 $D=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，向量 $x_i\in {\mathbb{R}}^p$ 为样本，$y_i\in \mathbb{R}$ 为标签，$i=1,2,\dots ,n$；$W\in {\mathbb{R}}^p$ 为模型参数（权重）。

记
$$\begin{gathered} X={\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)}^T=\left(\begin{array}{c}{x}_1^T\\ x_2^T\\ ⋮\\ x_n^T\end{array}\right)={\left(\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1p}\\ x_{11}& x_{12}& \dots & x_{2p}\\ ⋮& ⋮& & ⋮\\ x_{n1}& x_{n2}& \dots & x_{np}\end{array}\right)}_{n\times p} \\ Y={\left(\begin{array}{cccc}{y}_1& y_2& \dots & y_n\end{array}\right)}_{n\times 1}^T \\ W={\left(\begin{array}{cccc}{w}_1& w_2& \dots & w_p\end{array}\right)}_{p\times 1}^T \end{gathered}$$

1. 线性回归

1.1. 定义

模型定义为
$$f(\alpha )=w_0+w_1{\alpha }_1+\cdots +w_p{\alpha }_p$$
其中样本 $\alpha \in {\mathbb{R}}^p$，对应标签 $y$ ，$w_0$ 为偏置项。一般为了统一处理，认为样本为 $p+1$ 维，在 $x_i$（或 $X$） 的第一维添加 $x_0=1$，在 $W$ 的第一维添加 $w_0$ 。线性回归模型的目标是找到模型参数 $W$ 使得每个样本对应的输出值 $f(\alpha )=W^T\alpha$ 都尽可能地贴近其标签 $y$。

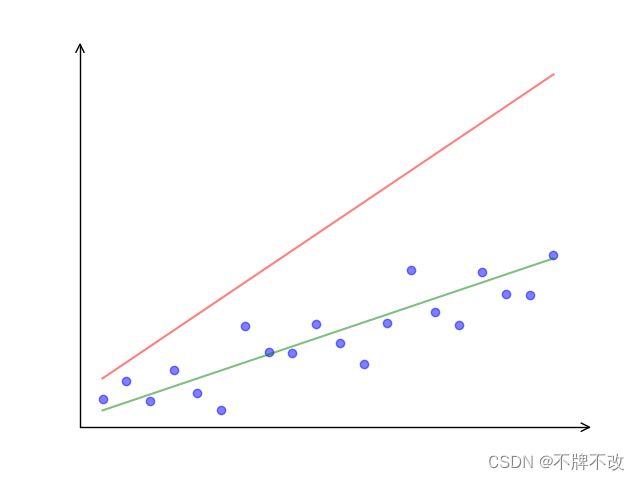
直观上，图 $1$ 中的绿线显然比红线更加贴近样本点，故认为绿线对应的模型参数比红线对应的模型参数更符合预期。

图 1    二维线性回归拟合曲线例图

2. 最小二乘估计

为了方便讲解，不妨忽略掉偏置项。

2.1. 矩阵形式

最小二乘估计（Least Square Estimate，LSE）是训练线性回归模型常用的方法，这个方法对应着一个目标函数
$$\begin{array}{rl}L(W)& =\sum _{i=1}^n||W^T{x}_i-y_i|{|}_2^2\\ & =\sum _{i=1}^n(W^T{x}_i-y_i{)}^2\end{array}\text{\hspace{1em}(1)}$$

$||\cdot |{|}_2$ 表示二范数，$||\cdot |{|}_2^2$ 表示二范数的平方。

其他一些资料中可能会在目标函数中添加一些系数，本质上都是等价的。

将式 $(1)$ 以矩阵形式表示
$$\begin{array}{rl}L(W)& =\sum _{i=1}^n(W^T{x}_i-y_i{)}^2\\ & =\left(\begin{array}{cccc}{W}^T{x}_1-y_1& W^T{x}_2-y_2& \dots & W^T{x}_n-y_n\end{array}\right){\left(\begin{array}{cccc}{W}^T{x}_1-y_1& W^T{x}_2-y_2& \dots & W^T{x}_n-y_n\end{array}\right)}^T\\ & =[W^T\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)-\left(\begin{array}{cccc}{y}_1& y_2& \dots & y_n\end{array}\right)][W^T\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)-\left(\begin{array}{cccc}{y}_1& y_2& \dots & y_n\end{array}\right){]}^T\\ & =(W^T{X}^T-Y^T)(XW-Y)\\ & =W^T{X}^{T}XW-W^T{X}^{T}Y-Y^{T}XW+Y^{T}Y\\ & =W^T{X}^{T}XW-2W^T{X}^{T}Y+Y^{T}Y\end{array}\text{\hspace{1em}(2)}$$

解释最后一步化简，根据矩阵乘法规则可知，$W^T{X}^{T}Y$ 和 $Y^{T}XW$ 的结果为 $1\times 1$ 矩阵即常数，且二者互为转置矩阵，因此 $W^T{X}^{T}Y=Y^{T}XW$。故最后一步将二者合并。

最小化目标函数 $(2)$ 对应的 $W$ 为目标模型参数，即
$$\hat{W}=\arg \underset{W}{\min }L(W)\text{\hspace{1em}(3)}$$
对 $L(W)$ 求导，并令导数为零
$$\frac{\partial L(W)}{\partial W}=2X^{T}XW-2X^{T}Y=0$$
令导数为零，可得解析解
$$W=(X^{T}X{)}^{-1}{X}^{T}Y\text{\hspace{1em}(4)}$$
其中，$(X^{T}X{)}^{-1}{X}^T$ 称为 $X$ 的伪逆。

伪逆的相关知识参考 REF [3]。

更准确地讲，$(X^{T}X{)}^{-1}{X}^T$ 是 $X$ 的左逆矩阵。

我认为，在不采用迭代法的前提下，如果 $X$ 不存在左逆矩阵，应该可以计算 M-P 广义逆矩阵作为最优解。

2.2. 几何意义

根据式 $(1)$ 很容易看出最小二乘估计的其中一种几何解释。最小二乘估计规定了具体度量误差的方式，每个样本投入模型的输出值与标签的差值平方和作为总误差，用于评估模型优劣和训练模型参数。

另外，还可以从向量空间的角度来理解其几何意义。
$$\begin{array}{rl}{X}_{n\times p}{W}_{p\times 1}& =\hat{Y}\\ \left(\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1p}\\ x_{11}& x_{12}& \dots & x_{2p}\\ ⋮& ⋮& & ⋮\\ x_{n1}& x_{n2}& \dots & x_{np}\end{array}\right)\left(\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_p\end{array}\right)& =\left(\begin{array}{c}{\hat{y}}_1\\ {\hat{y}}_2\\ ⋮\\ {\hat{y}}_n\end{array}\right)\\ w_1\left(\begin{array}{c}{x}_{11}\\ x_{21}\\ ⋮\\ x_{n1}\end{array}\right)+w_2\left(\begin{array}{c}{x}_{12}\\ x_{22}\\ ⋮\\ x_{n2}\end{array}\right)+\cdots +w_p\left(\begin{array}{c}{x}_{1p}\\ x_{2p}\\ ⋮\\ x_{np}\end{array}\right)& =\left(\begin{array}{c}{\hat{y}}_1\\ {\hat{y}}_2\\ ⋮\\ {\hat{y}}_n\end{array}\right)\end{array}$$
其中，$\hat{Y}={\left(\begin{array}{cccc}{\hat{y}}_1& {\hat{y}}_2& \dots & {\hat{y}}_n\end{array}\right)}^T$ 为样本投入模型的预测值，区别于标签 $Y={\left(\begin{array}{cccc}{y}_1& y_2& \dots & y_n\end{array}\right)}^T$ 。

向量 ${\alpha }_i={\left(\begin{array}{cccc}{x}_{1i}& x_{2i}& \dots & x_{ni}\end{array}\right)}^T,i=1,2,\dots ,p$ 在 $n$ 维空间 $U$ 中，$p$ 个向量所张成的空间维度最大不超过 $p$，因为样本数 $n$ 一般远大于样本向量的维度 $p$，所以 $p$ 个向量所张成的空间为 $n$ 维空间的子空间，该不超过 $p$ 维的子空间记为 $V$。由解方程 $XW=\hat{Y}$ 的几何意义可知， $\hat{Y}$ 相当于向量 ${\alpha }_i,i=1,2,\dots ,p$ 的一种线性组合，组合系数为 $W$，这说明 $\hat{Y}$ 在 $V$ 中。如果标签 $Y$ 也在子空间 $V$ 中，那么 $Y$ 显然可以由 ${\alpha }_i$ 线性组合得到，因此目标 $W$ 应该能使得 $XW=\hat{Y}=Y$，此时最小二乘估计对应的目标函数值为 $0$ ，但是实际中这种情况不大可能出现；大多数情况下，标签 $Y$ 不在 $V$ 中，或者说不能由 ${\alpha }_i$ 线性表示，那么最小二乘估计的几何意义为在子空间 $V$ 中找到一个距离空间 $U$ 中向量 $Y$ 的最近向量 $\hat{Y}$。直观上来说，$\hat{Y}$ 为 $Y$ 向子空间 $V$ 的投影向量时，二者最为接近，了解一些降维算法的同学应该知道投影可以保留 $Y$ 在子空间 $V$ 的全部信息；也可以从计算方面简单证明，当 $\hat{Y}$ 为投影向量时，向量 $Y-\hat{Y}$ 与子空间 $V$ 中的任意一个向量均垂直，故有 $X^T(Y-\hat{Y})=X^T(Y-XW)=O_{p\times 1}$，$O_{p\times 1}$ 为 $p$ 为零向量，可以解得 $W=(X^{T}X{)}^{-1}{X}^{T}Y$，这与最小二乘估计的解析解式 $(4)$ 不谋而合。可见，子空间 $V$ 中的目标向量就是 $Y$ 的投影向量。

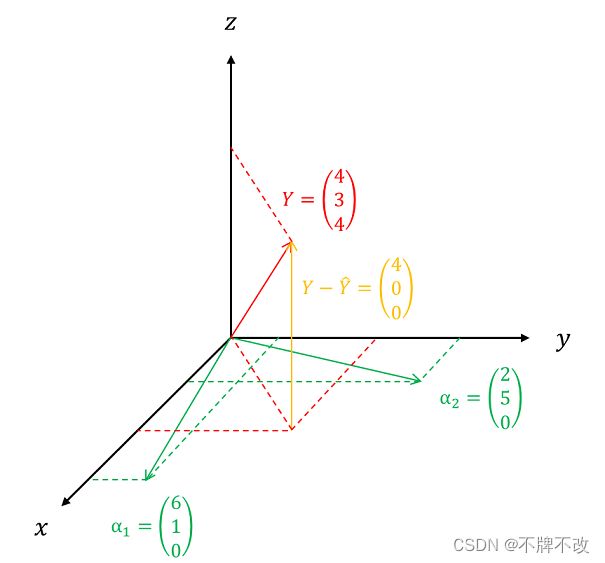
对于上述关于子空间和投影不理解的同学，可以通过下面的例图来配合思考。

图 2    最小二乘估计几何意义例图

总而言之，定义最小二乘估计的目标函数考虑到了第一种几何意义，也是目标函数直接表达出来的含义；第二种几何意义是从解方程、向量空间的角度来理解，更加抽象，但是有助于我们从不同角度来体会最小二乘估计的优美。

2.3. 概率视角下的朴素最小二乘估计

下面从频率派学者的角度（MLE）来重新审视最小二乘估计（LSE）。

从上面的几何意义可以看出，$Y$ 能够由 ${\alpha }_i$ 线性表示的可能性不大，因为数据本身就具有随机性，带有一定的噪声。假设每个数据的噪声都服从正态分布 $ϵ\sim N(0,{\sigma }^2)$ ，标签 $Y$ 可以表示为噪声形式 $Y=\hat{Y}+ϵ=W^{T}X+ϵ$。按照频率派学者的认知，这里的样本 $X$ 是已知量，模型参数 $W$ 是未知常数，噪声 $ϵ$ 是随机变量，标签 $Y$ 是观测结果，因此 $Y\mid X,W\sim N(W^{T}X,{\sigma }^2)$ ，对应的概率分布函数为
$$P(Y\mid X,W)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(Y-W^{T}X{)}^2}{2{\sigma }^2}}\text{\hspace{1em}(5)}$$
注意，式 $(2)$ 其实是 $n$ 个正态分布连乘的简便记号，原型为
$$P(Y\mid X,W)=\prod _{i=1}^{n}P(y_i\mid x_i,W)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}}\text{\hspace{1em}(6)}$$
利用频率派的极大似然估计（MLE）定义目标函数
$$\begin{array}{rl}L(W)& =\log P(Y\mid X,W)\\ & =\log \prod _{i=1}^{n}P(y_i\mid x_i,W)\\ & =\sum _{i=1}^n\log P(y_i\mid x_i,W)\\ & =\sum _{i=1}^n\log \left(\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}}\right)\\ & =\sum _{i=1}^n\log \frac{1}{\sqrt{2\pi }\sigma }+\sum _{i=1}^n\log e^{-\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}}\\ & =\sum _{i=1}^n\log \frac{1}{\sqrt{2\pi }\sigma }-\sum _{i=1}^n\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}\end{array}\text{\hspace{1em}(7)}$$
最大化目标函数 $(7)$ 对应的 $W$ 为目标模型参数，即
$$\begin{array}{rl}\hat{W}& =\arg \underset{W}{\max }L(W)\\ & =\arg \underset{W}{\max }\log P(Y\mid X,W)\\ & =\arg \underset{W}{\max }\sum _{i=1}^n\log \frac{1}{\sqrt{2\pi }\sigma }-\sum _{i=1}^n\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}\\ & =\arg \underset{W}{\max }-\sum _{i=1}^n\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}\\ & =\arg \underset{W}{\min }\sum _{i=1}^n\frac{(y_i-W^T{x}_i{)}^2}{2{\sigma }^2}\\ & =\arg \underset{W}{\min }\sum _{i=1}^n(y_i-W^T{x}_i{)}^2\end{array}$$
这与式 $(1)$ 完全相同，可见，以频率派学者的角度理解 LSE 可以推导出与 LSE 一般定义下相同的目标函数。因此，我们可以认为朴素最小二乘估计与噪声为高斯分布的最大似然估计是等价的。