【菜菜的sklearn课堂笔记】支持向量机-探索核函数在不同数据集上的表现
视频作者:菜菜TsaiTsai
链接:【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili
关于核函数在不同数据集上的研究甚少,谷歌学术上的论文中也没有几篇是研究核函数在SVM中的运用的,更多的是关于核函数在深度学习,神经网络中如何使用。在sklearn中,也没有提供任何关于如何选取核函数的信息。
接下来我们就通过一个例子,来探索一下不同数据集上核函数的表现。我们现在有一系列线性或非线性可分的数据,我们希望通过绘制SVC在不同核函数下的决策边界并计算SVC在不同核函数下分类准确率来观察核函数的效用。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.svm import SVC
from sklearn.datasets import make_circles, make_moons, make_blobs, make_classification
n_samples = 100
dataset = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),
make_classification(n_samples=n_samples, n_features=2, n_informative=2, n_redundant=0, random_state=5)
]
Kernel = ["linear", 'poly', 'sigmoid', 'rbf']
for X,Y in dataset:
plt.figure(figsize=(5,4))
plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
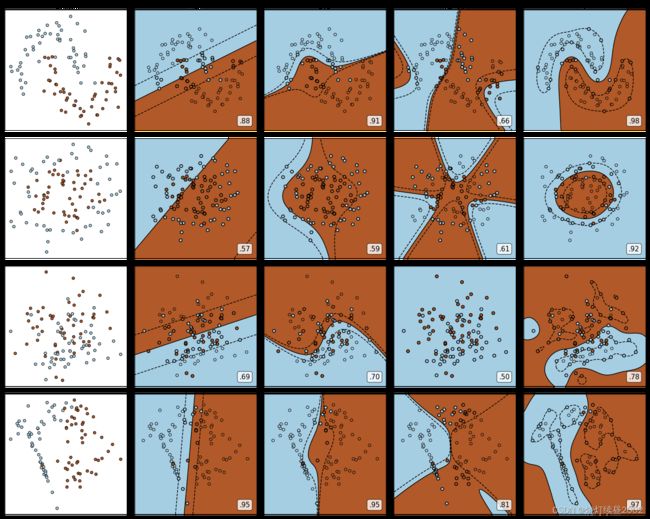
我们总共有四个数据集,四种核函数,我们希望观察每种数据集下每个核函数的表现。以核函数为列,以图像分布为行,我们总共需要16个子图来展示分类结果。而同时,我们还希望观察图像本身的状况,所以我们总共需要20个子图,其中第一列是原始图像分布,后面四列分别是这种分布下不同核函数的表现。
nrows = len(dataset)
ncols = len(Kernel) + 1
fig, axes = plt.subplots(nrows,ncols,figsize=(20,16))
[*enumerate(dataset)]
# 结果是[(索引,(样本特征集,样本标签集))]
# 因为很长这里就不展示详细什么样子了
[*enumerate(Kernel)]
---
[(0, 'linear'), (1, 'poly'), (2, 'sigmoid'), (3, 'rbf')]
fig, axes = plt.subplots(nrows,ncols,figsize=(20,16))
# 第一层循环:在不同的数据集中循环
# 我们不仅想取到元素,还想取到序号
# [*惰性对象] 能打开的还有map,zip也都是惰性对象
# list(enumerate(dataset))==[*enumerate]
for ds_cnt, (X, Y) in enumerate(dataset):
# 在图像中的第一列,放置原数据的分布
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data") # 第一列第一行的图的标题,表示这一整列的标题
ax.scatter(X[:,0],X[:,1],c=Y
,zorder=10,cmap=plt.cm.Paired,edgecolors="k"
)
# zorder:指定图像图层。数字越大图层越靠上
# edgecolors:点边缘的颜色
ax.set_xticks([])
ax.set_yticks([])
# 第二层循环:在不同的核函数中循环
# 从图像的第二列开始,一个个填充分列结果
for est_idx, kernel in enumerate(Kernel):
# 定义子图位置
ax = axes[ds_cnt, est_idx + 1] # 行索引是不变的
# 建模
clf = SVC(kernel=kernel, gamma=2).fit(X,Y)
score = clf.score(X,Y)
# 绘制图像本身的散点图
ax.scatter(X[:,0],X[:,1],c=Y
,zorder=10,cmap=plt.cm.Paired,edgecolors="k"
)
# 绘制支持向量
ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=50
,facecolors="none",zorder=10,edgecolors='k')
# facecolors:none值即点为透明的
# 因为我们这里想要画一个圈在支持向量上来表示支持向量的位置,而不是盖住支持向量
# 绘制决策边界
x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
# 在原本区间的基础上最大最小各增大0.5
y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
# np.mgrid,合并了之前使用的np.linspace和np.meshgrid的用法
# 一次性使用最大值和最小值来生成网格
# 表示为[起始值:结束值:步长],注意中间是分号,整体是方括号而不是小括号
# 如果步长是复数,则其整数部分就是起始值和结束值之间创建的点的数量,并且结束值被包含在内
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
# 200j就是复数,这里用于指定200个点
# 生成的XX也就是np.mgrid返回的第一个元素每一行是同一个数,YY每一列是同一个数
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
# np.c_类似np.vstack.T
# 需要reshape是因为返回的是一维的array,而contour需要的是与XX,YY维度对应的矩阵
# 填充等高线不同区域的颜色
ax.pcolormesh(XX,YY,Z > 0, cmap=plt.cm.Paired)
# 实际上就是区分决策边界的两侧
# 绘制等高线
ax.contour(XX,YY,Z,colors=['k','k','k'],linestyles=['--','-','--']
,levels=[-1,0,1])
ax.set_xticks([])
ax.set_yticks([])
# 将标题放在第一行的顶上
if ds_cnt == 0:
ax.set_title(kernel)
# 为每张图添加分类的分数
ax.text(0.95, 0.06
,('%.2f' %score).lstrip('0')
,size=15
,bbox=dict(boxstyle='round',alpha=0.8,facecolor='white')
,transform=ax.transAxes
,horizontalalignment='right')
# 0.95,0.06:文字所在x,y轴的位置。这里是添加在右下角
# 第三个参数,要添加的文字
# %.2f保留两位小数,结果是str,而不是float
# lstrip('0')不要显示0.xx,显示.xx,前面的对象要是str,而不是float
# bbox:添加格子,后面的字典指定盒子的样式
# boxstyle:格子角是圆的
# facecolor:将分数添加一个白色的格子作为底色
# transform=ax.transAxes:确定文字所对应的坐标轴,就是ax子图的坐标轴本身
# horizontalalignment='right':位于坐标轴的右侧方向
plt.tight_layout()
# 图像之间空格尽量小,紧缩
plt.show()
# 会报一个warning
# UserWarning: No contour levels were found within the data range.warnings.warn("No contour levels were found"
# 猜测应该是应该是第三行第四列的图,因为完全没有画决策边界(sigmoid:“开摆”)
# 对于第三行混杂的数据可以考虑决策树
可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果是像环形数据那样彻底不可分的,则表现糟糕。在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。另外,多项式核函数多被用于图像处理之中。
Sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如rbf,它在线性数据上完全比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。
rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。
我个人的经验是,无论如何先试试看高斯径向基核函数,它适用于核转换到很高的空间的情况,在各种情况下往往效果都很不错,如果rbf效果不好,那我们再试试看其他的核函数。
几个函数单独拎出来大概展示一下是干啥的
np.mgrida, b = np.mgrid[1:3:3j, 2:4:3j] print(a) print(b) --- [[1. 1. 1.] [2. 2. 2.] [3. 3. 3.]] [[2. 3. 4.] [2. 3. 4.] [2. 3. 4.]]np.c_[]和np.vstack
np.c_[[1,2,3],[2,3,4]] # 逐行连接,矩阵增长,并且转置 --- array([[1, 2], [2, 3], [3, 4]]) np.vstack([[1,2,3],[2,3,4]]) # 逐行连接,矩阵增长 --- array([[1, 2, 3], [2, 3, 4]]) (np.c_[[1,2,3],[2,3,4]] == np.vstack([[1,2,3],[2,3,4]]).T).all() # np.c_[]等价于np.vstack([]).T --- True格式化字符串
a = 0.01 ('%.2f' %a).lstrip('0') # 去掉0.前面的0 --- '.01' type('%.2f' %a) --- str
记录一下生活
有个同学复读了,今年刚上大一,昨天问我一个关于间断点的填空题,她问我,这个空为啥填连续型间断点是错的
你猜它为什么叫间断点