详解十大经典机器学习算法——EM算法

本文始发于个人公众号：TechFlow，原创不易，求个关注

今天是机器学习专题的第14篇文章，我们来聊聊大名鼎鼎的EM算法。

EM算法的英文全称是Expectation-maximization algorithm，即最大期望算法，或者是期望最大化算法。EM算法号称是十大机器学习算法之一，听这个名头就知道它非同凡响。我看过许多博客和资料，但是少有资料能够将这个算法的来龙去脉以及推导的细节全部都讲清楚，所以我今天博览各家所长，试着尽可能地将它讲得清楚明白。

从本质上来说EM算法是最大似然估计方法的进阶版，还记得最大似然估计吗，我们之前介绍贝叶斯模型的文章当中有提到过，来简单复习一下。

最大似然估计

假设当下我们有一枚硬币，我们想知道这枚硬币抛出去之后正面朝上的概率是多少，于是我们抛了10次硬币做了一个实验。发现其中正面朝上的次数是5次，反面朝上的次数也是5次。所以我们认为硬币每次正面朝上的概率是50%。

从表面上来看，这个结论非常正常，理所应当。但我们仔细分析会发现这是有问题的，问题在于我们做出来的实验结果和实验参数之间不是强耦合的。也就是说如果硬币被人做过手脚，它正面朝上的概率是60%，我们抛掷10次，也有可能得到5次正面5次反面的概率。同理，如果正面朝上的概率是70%，我们也有一定的概率可以得到5次正面5次反面的结果。现在我们得到了这样的结果，怎么能说明就一定是50%朝上的概率导致的呢？

那我们应该怎么办呢，继续做实验吗？

显然不管我们做多少次实验都不能从根本上解决这个问题，既然参数影响的是出现结果的概率，我们还是应该回到这个角度，从概率上下手。我们知道，抛硬币是一个二项分布的事件，我们假设抛掷硬币正面朝上的概率是p，那么反面朝上的概率就是1-p。于是我们可以带入二项分布的公式，算出10次抛掷之后，5次是正面结果在当前p参数下出现的概率是多少。

于是，我们可以得到这样一条曲线：

也就是正面朝上的概率是0.5的时候，10次抛掷出现5次正面的概率最大。我们把正面朝上的概率看成是实验当中的参数，我们把似然看成是概率。那么最大似然估计，其实就是指的是使得当前实验结果出现概率最大的参数。

也就是说我们通过实验结果和概率，找出最有可能导致这个结果的原因或者说参数，这个就叫做最大似然估计。

原理理解了，解法也就顺水推舟了。

首先，我们需要用函数将实验结果出现的概率表示出来。这个函数的学名叫做似然函数(likelihood function)。

有了函数之后，我们需要对函数进行化简，比如一些多次进行的实验，需要对似然函数求对数，将累乘计算转化成累加运算等。

最后，我们对化简完的似然函数进行求导，令导数为0，找出极值点处参数的值，就是我们通过最大似然估计方法找到的最佳参数。

引入隐变量

以上只是最大似然估计的基础用法，如果我们把问题稍微变化一下，引入多一个变量，会发生什么情况呢？

我们来看一个经典的例子，同样是抛硬币，但是我们将题目的条件稍作修改，那么整个问题就会完全不同。

这个例子来源于阐述EM算法的经典论文：《Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm?. Nature biotechnology, 26(8), 897.》在这个例子当中，我们有A和B两枚硬币，其中A硬币正面朝上的概率是0.5，B硬币正面朝上的概率是0.4，我们随机从两枚硬币当中选取一枚进行实验。

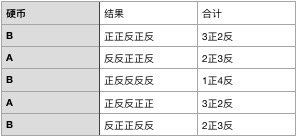
每次实验我们一共进行5次，记录下正反面的个数。经过5轮实验之后，我们得到的结果如下：

由于我们知道每一轮当中选择了什么硬币进行实验，所以整个过程依然非常顺利。如果我们去掉硬币的信息，假设我们并不知道每一轮当中选择了什么硬币进行实验，我们又该怎么求A和B向上的概率呢？

在新的实验当中，我们不知道硬币选择的情况，也就是说实验当中隐藏了一个我们无法得知的变量。这种变量称为隐变量，隐变量的存在干扰了参数和实验结果的直接联系。比如在这个问题当中，我们想要知道每种硬币正面向上的概率，我们要计算这个概率首先要知道每一轮用了哪一种硬币。如果我们想要推算每一次实验用了哪一种硬币又需要先知道硬币正面朝上的概率。也就是说这两个变量互相纠缠、互相依赖，我们已知的信息太少，无法直接解开。就好像先有鸡还是先有蛋的问题，陷入死循环。

EM算法正是为了解决这个问题诞生的。

EM算法

前面我们说了，隐变量和我们想要求的参数互相纠缠，形成了一个死循环，但是我们已有的信息不足以让我们解开这个纠缠。既然无法解开，那么我们就不解了，我们直接暴力破解。

是的，你没有看错，EM算法的本质非常简单粗暴：既然我们无法求解隐变量，我们就不求了，我们直接假设一个初始值代入计算，有了结果之后再进行迭代。

比如我们假设p1是硬币A正面向上的概率，p2是硬币B正面向上的概率。原本我们是希望通过最大似然估计来求解使得结果出现的p1和p2，现在我们直接假设，进行迭代：

我们假设p1=0.7，p2=0.3，这个值是我们随便假设的，你可以任意假设其他的值。我们把p1，p2代入上面的结果当中进行计算。

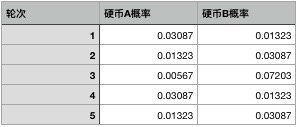
比如第一轮当中，出现的结果是3正2反，如果是A硬币，出现这样结果的概率根据二项分布很容易计算：$0.7^3\ast 0.3^2=0.03087$，同理，我们可以算出硬币B的概率是0.01323。我们用同样的方法算出所有的概率：

既然我们概率有了，显然我们可以做预测了，根据这个概率表猜测每一轮究竟用了哪一个硬币。

根据最大似然的法则，我们可以得出每一轮用的硬币是：

第一轮是硬币A

第二轮是硬币B

第三轮是硬币B

第四轮是硬币A

第五轮是硬币B

猜测出硬币的分布之后有什么用呢？很简单，我们可以用猜测的结果重新估计p1和p2的值。

比如说硬币A出现在第一轮和第四轮当中，这两轮一共做了10次实验，其中6正4反，那么我们可以修正p1的值为0.6。硬币B出现在第2，3，5轮当中，这三轮当中做了15次实验，一共5正10反，所以正面向上的概率是1/3。可以发现，经过了一次迭代之后，我们的结果向真实值逼近了一些。

虽然结果还可以，但这种方法依然比较粗糙，我们还有更好的办法。

例子改进

我们来改进一下上面这个例子的计算过程，主要的问题在于我们在根据假设出来的概率计算分布之后，我们直接通过似然估计去猜测当前轮次抛了哪一枚硬币。这样做当然是可以的，但感觉不够严谨，因为我们直接猜测有些武断，并不一定准确。

那有没有更好的办法？

其实是有的，相比于直接猜测某个轮次当中选择了哪一枚硬币，我们可以用选择硬币的概率来代入来计算期望，这样的效果会更好，比如根据刚才的计算结果，我们可以算出每个轮次当中选择硬币的概率：

我们在用这个概率带入实验结果当中计算期望，可以得到p1的期望表格：

$$p_1=\frac{2.1+0.6+0.0729+2.1+0.6}{2.7+2.7+0.292+2.7+2.7}=0.490$$

同样的方法，我们可以算计出新的p2的期望表格：

代入，我们可以得到新的p2是0.377。

把估计结果改成使用概率代入迭代之后，我们的估计的结果精准了许多，也就是说我们收敛的速度更快了。我们重复以上的过程，直到收敛，当收敛的时候，我们就能获得极大似然估计最大时候p1和p2的取值。这也是整个EM算法的精髓。

我们整理一下EM算法的运作过程，首先我们先随机出来一个参数的值代入实验结果，计算出隐变量的概率分布或者是取值，我们再通过隐变量迭代我们的参数值，如此重复迭代，直到收敛。我们进一步抽象，可以把它主要总结成两个步骤，分别是E步骤和M步骤：

在E步骤当中，我们根据假设出来的参数值计算出未知变量的期望估计，应用在隐变量上
在M步骤当中，我们根据隐变量的估计值，再计算当前参数的极大似然估计

根据这个理论，我们还可以对上面的过程进行改进。

这个方法到这里就介绍完了，我想大家也应该都能理解，但是我们还没有从数学上去证明，为什么这样操作行得通呢？为什么这个方法一定会收敛，我们收敛的值就是最优解呢？所以我们还需要通过数学来证明一下。

数学证明

假设我们有一个样本集X它是由m个样本构成的，可以写成$X=\{x_1,x_2,\cdots x_m\}$，对于这m个样本当中，它们都有一个隐变量z是未知的。并且还有一个参数$\theta$，也就是我们希望通过极大似然估计求解的参数。由于当中包含隐变量z，所以我们没办法直接对概率函数求导求极值进行计算。

我们先写出含有隐变量的概率函数：

$$P_i=P(x_i,z_i;\theta )$$

我们希望找到对于全局最优的参数$\theta$，所以我们希望找到使得${\prod }_{i=1}^m{P}_i$最大，我们对这个式子求log，可以得到：

$$\sum _{i=1}^m\log P_i=\sum _{i=1}^m\log \sum _{z_i}P(x_i,z_i;\theta )$$

我们假设隐变量z的概率分布是$Q_i$，所以上式可以变形为：

$$\sum _{i=1}^m\log P_i=\sum _{i=1}^m\log \sum _{z_i}{Q}_i(z_i)\frac{P(x_i,z_i;\theta )}{Q_i(z_i)}$$

到这里似乎卡住了，其实没有，我们在之前的文章当中写过，对于凸函数有Jensen不等式：E[f(x)] >= f(E[x])，即函数的期望值大于等于期望值的函数值。而对数函数是广义上的凸函数，严格意义上的凹函数，它可以使用Jensen不等式，但是不等号的方向需要变号。

而上式当中$Q_i(z_i)$是隐变量的概率分布，所以${\sum }_{z_i}{Q}_i(z_i)[\frac{P(x_i,z_i;\theta )}{Q_i(z_i)}]$是$\frac{P(x_i,z_i;\theta )}{Q_i(z_i)}$的期望，于是我们可以代入Jensen不等式得到：

$$\sum _{i=1}^m\log P_i\ge \sum _{i=1}^m\sum _{z_i}{Q}_i(z_i)\log \frac{P(x_i,z_i;\theta )}{Q_i(z_i)}$$

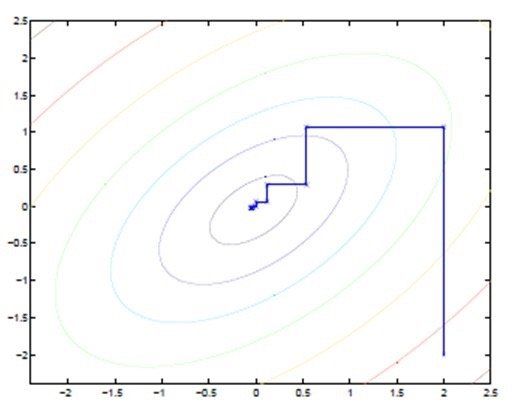
上面这个不等号右边的式子就容易求解多了，当我们固定z变量的时候，我们可以很方便地求解似然最大时的参数$\theta$。同理当我们有了$\theta$的取值之后，又可以来优化z。这种两个变量固定一个，轮流优化另一个的方法叫做坐标上升法，也是机器学习当中非常常用的求解方式。

如上图所示，这个一圈一圈的是损失函数的等高线。当我们使用坐标上升法的时候，我们每次固定一个轴的变量，优化另一个变量，然后交替进行，我们同样可以得到全局最优解。

除此之外，我们也可以从数学上进行解释。

由于上面的式子是一个不等式，我们没有办法直接求解左边的最值，所以我们通过不断优化右边式子的方法来逼近左边的最值。我们令左边的一串式子是$L(\theta )$，不等号右边的式子是$J(z,\theta )$，然后我们来看一张图，这张图是我从大神的博客里找来的神图：

上图当中最上方的红色是$L(\theta )$，下面的图像是J。我们每次固定z，都可以找到一个更好的$\theta$，使得$J(z,\theta )$朝着高点不断逼近，最终达到它的最大值。

直觉上这是OK的，但是我们还需要从数学上来证明。

根据Jensen不等式，只有当自变量x是常数的时候才可以取等，我们的自变量是$\frac{P(x_i,z_i;\theta )}{Q_i(z_i)}$，我们令它等于常数c：

$$\frac{P(x_i,z_i,\theta )}{Q_i(z_i)}=c$$

由于${\sum }_{z_i}{Q}_i(z_i)=1$，所以我们可以知道${\sum }_{z_i}P(x_i,z_i,\theta )=c$，我们代入上式，可以得到：

$$\begin{array}{rl}{Q}_i(z_i)\cdot c& =P(x_i,z_i,\theta )\\ Q_i(z_i)& =\frac{P(x_i.z_i;\theta )}{c}\\ Q_i(z_i)& =\frac{P(x_i.z_i;\theta )}{{\sum }_{z_i}P(x_i,z_i;\theta )}\\ Q_i(z_i)& =\frac{P(x_i.z_i;\theta )}{P(x_i;\theta )}\\ Q_i(z_i)& =P(z_i|x_i;\theta )\end{array}$$

经过这一串变形之后，我们得到了$Q_i(z_i)$的计算公式其实是一个后验概率。这一步也就是我们刚才介绍的E步，之后，在确定了$Q_i(z_i)$之后，我们来求导求极值的方法求使得函数最大时的$\theta$，也就是刚才的M步。

所以，整个EM算法的过程就是重复这个过程，直到收敛。

那么我们又该怎么保证算法能够一定收敛呢？其实也不难，由于我们在进行E步骤的时候遵循了Jensen不等式的取等条件求出的z，所以可以保证能够取到等号，也就是：

$$L({\theta }_t)=\sum _{i=1}^m\sum _{z_i}{Q}_i(z_i)\log \frac{P(x_i,z_i;{\theta }_t)}{Q_i(z_i)}$$

当我们固定$Q_i(z_i)$求导得到极大化的参数${\theta }_{t+1}$之后，我们得到右式，一定是优于$L(\theta )$的，但是我们不能确定对于新的${\theta }_{t+1}$，我们之前的$Q_i(t_i)$的分布也能满足Jensen不等式的取等条件，所以：

$$\begin{array}{rl}L({\theta }_{t+1})& \ge \sum _{i=1}^m\sum _{z_i}{Q}_i(z_i)\log \frac{P(x_i,z_i;{\theta }_{t+1})}{Q_i(z_i)}\\ & \ge \sum _{i=1}^m\sum _{z_i}{Q}_i(z_i)\log \frac{P(x_i,z_i;{\theta }_t)}{Q_i(z_i)}\\ & =L(\theta )\end{array}$$

这样我们就证明了似然函数的取值是在递增的，当最后收敛的时候，就是最大似然估计时的值，此时的参数$\theta$就是我们需要的最大似然估计方法得出的参数。

总结

到这里，EM算法就算是介绍完了。整个算法给我最大的感受是这又是一个建立在数学推导上的算法，它的推导过程非常严谨，效果也非常好，通过它可以解决很多直观上无法解决的问题。并且更难得的是，即使我们抛弃掉数学上严谨的证明和推导，也不妨碍我们直观地理解算法的思路。难怪该算法可以列入十大机器学习算法之一，的确非常经典。

最后，不知道大家在看的时候有没有一种感觉，就是EM算法的思路好像之前在什么地方见到过？有种似曾相识的感觉？

有这种感觉是对的，如果你回想一下之前讲的Kmeans，你会发现我们好像也是一开始的时候由于不知道聚类的中心进行了猜测。然后通过迭代一点一点地逼近。如果再多想一点，可以发现Kmeans的计算过程是可以和EM算法的过程相印证的。通过建模我们是可以把Kmeans的问题转化成EM算法的模型，感兴趣的同学可以研究一下这个问题，当然也可以期待一下我们后续的文章。

最后，关于EM算法的内容就到这里，如果觉得有所收获，请顺手点个关注或者转发吧，你们的举手之劳对我来说很重要。