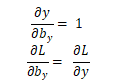独家 | 菜鸟必备的循环神经网络指南（附链接）

作者：Victor  Zhou

翻译：王雨桐

校对：吴金迪

本文约 3800字 ，建议阅读 15分钟 。

本文将介绍最基础的循环神经网络（Vanilla RNNs）的概况，工作原理，以及如何在Python中实现。

循环神经网络（RNN）是一种专门处理序列的神经网络。由于在处理文本时十分高效，它经常用于自然语言处理(NLP)。在接下来的文章中，我们将探讨RNN是什么，了解它的工作原理，并使用Python从零开始构建一个真正的RNN（仅使用numpy）。

在另一篇文章中，我介绍了一些神经网络的基本知识。本文对基础部分不做过多介绍，如有需要，建议先阅读基础文章。

附链接：

https://victorzhou.com/blog/intro-to-neural-networks/

 

让我们开始吧！

 

1. 为什么要用RNNs?

 

关于原始的神经网络（同样对于CNNs）的一个问题是它们只能使用预定大小的输入和输出：它们采用固定大小的输入并生成固定大小的输出。相比之下，RNNs可以将可变长度序列作为输入和输出。以下是RNN的示例：

 

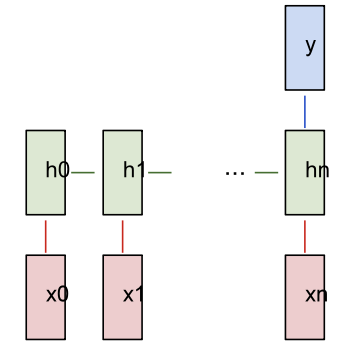
红色为输入，绿色为RNN本身，蓝色为输出。来源：Andrej Karpathy

 

这种处理序列的能力使RNN表现优异。例如：

• 机器翻译（例如Google翻译）使用“多对多”RNN。原始文本序列被送入RNN，随后RNN将翻译的文本作为输出。

• 情感分析（例如，这是一个积极的还是负面的评论？）通常是使用“多对一”RNN。将要分析的文本送入RNN，然后RNN产生单个输出分类（例如，这是一个积极的评论）。

 

在本文后面，我们将从零开始构建“多对一”RNN，并完成基本的情感分析。

 

2. 如何使用RNNs

让我们来看看“多对多”RNN吧！ 

1. 基于之前的隐藏状态和下一个输入，我们可以得到下一个隐藏状态。

2. 通过计算, 我们可以得到下一个输出 。

多对多 RNN

这就是使RNN循环的过程：每一步都会使用相同的权重。 更具体地说，典型的原始RNN仅使用3组权重就能完成计算：

此外， 我们还要在RNN中引入两个偏移量：

我们用矩阵表示权重，用向量表示偏差。这3个权重和2个偏差就构成了整个RNN！

以下是将所有内容组合在一起的公式：

 

不要略过这些方程式。 停下来一分钟看看它。 另外，要时刻牢记权重是矩阵，其他变量是向量。

我们在矩阵乘法中应用所有的权重，并将偏差添加到所得结果中。然后我们将tanh作为第一个等式的激活函数（也可以使用其他激活，如sigmoid）。

3. 问题

 

接下来我们将从零开始应用RNN来执行简单的情感分析任务：确定给定的文本的情感是正向的还是负向的。

 

以下是我为本文整理的数据集中的一些示例：

 

附数据集链接：

https://github.com/vzhou842/rnn-from-scratch/blob/master/data.py

 

Text	Positive?
i am good	✓
i am bad	❌
this is very good	✓
this is not bad	✓
i am bad not good	❌
i am not at all happy	❌
this was good earlier	✓
i am not at all bad or sad right now	✓

4. 计划

 

由于这是一个分类问题，我们将使用“多对一”RNN。这和我们之前讨论过的“多对多”RNN类似，但不同的是它只使用最终隐藏状态输出一个y：

 

多对一 RNN

 

每个都是一个表示文本中单词的向量。输出的y向量将包含两个数字，一个表示积极态度，另一个表示消极态度。我们将应用Softmax将这些值转换为概率，并最终在积极/消极之间做出决定。

 

让我们开始实现RNN吧！

 

5. 预处理

 

前文提到的数据集由两部分组成。

 

data.py

train_data = {

  'good': True,

  'bad': False,

  # ... more data

}

 

test_data = {

  'this is happy': True,

  'i am good': True,

  # ... more data

}

True=积极，False=消极

 

我们必须进行一些预处理才能将数据转换为可用的格式。首先，我们构建词汇表，用来存放数据中出现的词汇：

 

main.py

from data import train_data, test_data

 

# Create the vocabulary.

vocab = list(set([w for text in train_data.keys() for w in text.split(' ')]))

vocab_size = len(vocab)

print('%d unique words found' % vocab_size) # 18 unique words found

 

现在，vocab这个列表中包含了所有的单词，这里是指至少在一个训练样本中出现的单词。接下来，为了表示词汇表中的每个单词，我们将设定一个整数索引。

 

main.py

# Assign indices to each word.

word_to_idx = { w: i for i, w in enumerate(vocab) }

idx_to_word = { i: w for i, w in enumerate(vocab) }

print(word_to_idx['good']) # 16 (this may change)

print(idx_to_word[0]) # sad (this may change)

 

我们现在可以用相应的整数索引表示任何给定的单词！这是必要的步骤，因为RNN无法理解单词，所以我们必须给它输入数字。

 

最后，回想一下RNN的每个输入是一个向量。我们将使用独热编码，其中包含除了单个一之外的所有零。每个独热向量中的“1”将位于单词的相应整数索引处。

 

由于我们的词汇表中有18个唯一的单词，每个将是一个18维的单热矢量。

 

main.py

import numpy as np

 

def createInputs(text):

  '''

  Returns an array of one-hot vectors representing the words

  in the input text string.

  - text is a string

  - Each one-hot vector has shape (vocab_size, 1)

  '''

  inputs = []

  for w in text.split(' '):

    v = np.zeros((vocab_size, 1))

    v[word_to_idx[w]] = 1

    inputs.append(v)

  return inputs

随后，我们将用createInputs（）来生成输入向量，并传入到RNN中。

 

6. 向前传播阶段

 

是时候开始实现我们的RNN了！我们首先将初始化RNN需要的3个权重和2个偏移量：

 

rnn.py

import numpy as np

from numpy.random import randn

 

class RNN:

  # A Vanilla Recurrent Neural Network.

 

  def __init__(self, input_size, output_size, hidden_size=64):

    # Weights

    self.Whh = randn(hidden_size, hidden_size) / 1000

    self.Wxh = randn(hidden_size, input_size) / 1000

    self.Why = randn(output_size, hidden_size) / 1000

 

    # Biases

    self.bh = np.zeros((hidden_size, 1))

    self.by = np.zeros((output_size, 1))

注意：我们除以1000以减少权重的初始方差。尽管这不是初始化权重的最佳方法，但它很直观，适用于这篇文章。

 

我们使用np.random.randn（），基于标准正态分布初始化权重。

接下来，让我们实现RNN前向传播。 还记得我们之前看到的这两个方程吗?

 

以下是在代码中的实现：

 

rnn.py

class RNN:

  # ...

 

  def forward(self, inputs):

    '''

    Perform a forward pass of the RNN using the given inputs.

    Returns the final output and hidden state.

    - inputs is an array of one hot vectors with shape (input_size, 1).

    '''

    h = np.zeros((self.Whh.shape[0], 1))

 

    # Perform each step of the RNN

    for i, x in enumerate(inputs):

      h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)

 

    # Compute the output

    y = self.Why @ h + self.by

 

    return y, h

 

这很简单吧？ 请注意，因为没有之前的h可以使用，我们在第一步中将h初始化为零向量。

 

让我们来试试吧：

 

main.py

# ...

 

def softmax(xs):

  # Applies the Softmax Function to the input array.

  return np.exp(xs) / sum(np.exp(xs))

 

# Initialize our RNN!

rnn = RNN(vocab_size, 2)

 

inputs = createInputs('i am very good')

out, h = rnn.forward(inputs)

probs = softmax(out)

print(probs) # [[0.50000095], [0.49999905]]

如果需要复习Softmax相关知识，可以通过链接阅读相关的快速解释。

附链接：

https://victorzhou.com/blog/softmax/

 

我们的RNN可以成功运行，但它看起来不是很有用。 看来我们得作出一些改变......

 

7. 反馈阶段

 

为了训练RNN，首先我们需要一个损失函数。我们将使用交叉熵损失函数，它通常与Softmax结合。 计算公式如下：

 

 

现在我们有了损失函数，我们将使用梯度下降来训练RNN模型，以尽量减少损失。 这意味着我们现在要做一些梯度相关的计算！

 

以下部分需要一些多变量微积分的基本知识，你可以选择跳过这部分。即使你不太了解，我也建议你大概浏览一下。推导出结果后，我们将逐步完成代码，浅层次的理解也会有所帮助。

 

如果想要深入了解本节，可以阅读我在“神经网络介绍”一文中的“训练神经网络”部分。 此外，本文的所有代码都在Github上，你也可以在Github上关注我。

附Github链接：

https://github.com/vzhou842/rnn-from-scratch

 

7.1定义

首先，我们要明确一些定义：

7.2 准备

接下来，我们需要编辑向前传播阶段并缓存一些数据，以便在反馈阶段使用。在我们处理它的同时，我们还将为我们的反馈阶段设置框架。大致如下所示：

rnn.py

class RNN:

  # ...

 

  def forward(self, inputs):

    '''

    Perform a forward pass of the RNN using the given inputs.

    Returns the final output and hidden state.

    - inputs is an array of one hot vectors with shape (input_size, 1).

    '''

    h = np.zeros((self.Whh.shape[0], 1))

 

    self.last_inputs = inputs    self.last_hs = { 0: h }

    # Perform each step of the RNN

    for i, x in enumerate(inputs):

      h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)

      self.last_hs[i + 1] = h

    # Compute the output

    y = self.Why @ h + self.by

 

    return y, h

 

  def backprop(self, d_y, learn_rate=2e-2):

'''    

Perform a backward pass of the RNN.    

- d_y (dL/dy) has shape (output_size, 1).    

- learn_rate is a float.    

'''    

pass

 

7.3 梯度

现在开始是数学登场的时候啦！我们要开始计算

 

通过链式法则计算的过程就作为练习吧，结果如下：

 

main.py

# Loop over each training example

for x, y in train_data.items():

  inputs = createInputs(x)

  target = int(y)

 

  # Forward

  out, _ = rnn.forward(inputs)

  probs = softmax(out)

 

  # Build dL/dy

  d_L_d_y = probs  d_L_d_y[target] -= 1

  # Backward

  rnn.backprop(d_L_d_y)

接下来，让我们完成和的梯度计算，这仅用于将最终隐藏状态转换为RNN的输出。 我们有：

 

 

是最终的隐藏状态。因此，

 

同样的，

 

我们现在可以开始应用backprop（）！

 

rnn.py

class RNN:

  # ...

 

  def backprop(self, d_y, learn_rate=2e-2):

    '''

    Perform a backward pass of the RNN.

    - d_y (dL/dy) has shape (output_size, 1).

    - learn_rate is a float.

    '''

    n = len(self.last_inputs)

 

    # Calculate dL/dWhy and dL/dby.

d_Why = d_y @ self.last_hs[n].T  

d_by = d_y

提示：我们之前在forward（）中创建了self.last_hs。

 

 

因为改变将影响每一个，这一切都会影响y和最终L。为了计算的梯度, 我们需要所有时间步长的反向传播，这称为反向传播时间（BPTT）：

 

 

rnn.py

class RNN:

  # …

 

  def backprop(self, d_y, learn_rate=2e-2):

‘’’

Perform a backward pass of the RNN.

- d_y (dL/dy) has shape (output_size, 1).

- learn_rate is a float.

‘’’

n = len(self.last_inputs)

 

# Calculate dL/dWhy and dL/dby.

D_Why = d_y @ self.last_hs[n].T

d_by = d_y

 

# Initialize dL/dWhh, dL/dWxh, and dL/dbh to zero.

D_Whh = np.zeros(self.Whh.shape)

d_Wxh = np.zeros(self.Wxh.shape)

d_bh = np.zeros(self.bh.shape)

 

# Calculate dL/dh for the last h.

d_h = self.Why.T @ d_y

 

# Backpropagate through time.

For t in reversed(range(n)):

      # An intermediate value: dL/dh * (1 – h^2)

      temp = ((1 – self.last_hs[t + 1] ** 2) * d_h)

 

      # dL/db = dL/dh * (1 – h^2)

      d_bh += temp

      # dL/dWhh = dL/dh * (1 – h^2) * h_{t-1}

      d_Whh += temp @ self.last_hs[t].T

      # dL/dWxh = dL/dh * (1 – h^2) * x

      d_Wxh += temp @ self.last_inputs[t].T

      # Next dL/dh = dL/dh * (1 – h^2) * Whh

      d_h = self.Whh @ temp

 

# Clip to prevent exploding gradients.

For d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:

      np.clip(d, -1, 1, out=d)

 

# Update weights and biases using gradient descent.

Self.Whh -= learn_rate * d_Whh

self.Wxh -= learn_rate * d_Wxh

self.Why -= learn_rate * d_Why

self.bh -= learn_rate * d_bh

self.by -= learn_rate * d_by

补充一些注意事项：

好啦！我们的RNN已经完成啦。

 

8. 高潮

终于等到了这一刻 - 让我们测试RNN吧！

首先，我们将编写一个帮助函数来处理RNN的数据：

main.py

import random

 

def processData(data, backprop=True):

  '''

  Returns the RNN's loss and accuracy for the given data.

  - data is a dictionary mapping text to True or False.

  - backprop determines if the backward phase should be run.

  '''

  items = list(data.items())

  random.shuffle(items)

 

  loss = 0

  num_correct = 0

 

  for x, y in items:

    inputs = createInputs(x)

    target = int(y)

 

    # Forward

    out, _ = rnn.forward(inputs)

    probs = softmax(out)

 

    # Calculate loss / accuracy

    loss -= np.log(probs[target])

    num_correct += int(np.argmax(probs) == target)

 

    if backprop:

      # Build dL/dy

      d_L_d_y = probs

      d_L_d_y[target] -= 1

 

      # Backward

      rnn.backprop(d_L_d_y)

 

  return loss / len(data), num_correct / len(data)

现在，我们可以完成一个训练的循环：

main.py

# Training loop

for epoch in range(1000):

  train_loss, train_acc = processData(train_data)

 

  if epoch % 100 == 99:

    print('--- Epoch %d' % (epoch + 1))

    print('Train:\tLoss %.3f | Accuracy: %.3f' % (train_loss, train_acc))

 

    test_loss, test_acc = processData(test_data, backprop=False)

    print('Test:\tLoss %.3f | Accuracy: %.3f' % (test_loss, test_acc))

运行 main.py应该会得到如下输出：

--- Epoch 100

Train:  Loss 0.688 | Accuracy: 0.517

Test:   Loss 0.700 | Accuracy: 0.500

--- Epoch 200

Train:  Loss 0.680 | Accuracy: 0.552

Test:   Loss 0.717 | Accuracy: 0.450

--- Epoch 300

Train:  Loss 0.593 | Accuracy: 0.655

Test:   Loss 0.657 | Accuracy: 0.650

--- Epoch 400

Train:  Loss 0.401 | Accuracy: 0.810

Test:   Loss 0.689 | Accuracy: 0.650

--- Epoch 500

Train:  Loss 0.312 | Accuracy: 0.862

Test:   Loss 0.693 | Accuracy: 0.550

--- Epoch 600

Train:  Loss 0.148 | Accuracy: 0.914

Test:   Loss 0.404 | Accuracy: 0.800

--- Epoch 700

Train:  Loss 0.008 | Accuracy: 1.000

Test:   Loss 0.016 | Accuracy: 1.000

--- Epoch 800

Train:  Loss 0.004 | Accuracy: 1.000

Test:   Loss 0.007 | Accuracy: 1.000

--- Epoch 900

Train:  Loss 0.002 | Accuracy: 1.000

Test:   Loss 0.004 | Accuracy: 1.000

--- Epoch 1000

Train:  Loss 0.002 | Accuracy: 1.000

Test:   Loss 0.003 | Accuracy: 1.000

我们自己制造的RNN也不错。

 

想亲自尝试或修补这些代码？你也可以在Github上找到。

附链接 ：

https://github.com/vzhou842/rnn-from-scratch

 

9. 总结

本文中，我们完成了回归神经网络的演练，包括它们是什么，它们如何工作，为什么它们有用，如何训练它们以及如何实现它们。不过，你还可以做更多的事情：

• 了解长短期记忆网络（LSTM），这是一个更强大和更受欢迎的RNN架构，或关于LSTM的著名的变体--门控循环单元（GRU）。

• 通过恰当的ML库（如Tensorflow，Keras或PyTorch），你可以尝试更大/更好的RNN。

• 了解双向RNN，它可以处理前向和后向序列，因此输出层可以获得更多信息。

• 尝试像GloVe或Word2Vec这样的Word嵌入，可用于将单词转换为更有用的矢量表示。

• 查看自然语言工具包（NLTK），这是一个用于处理人类语言数据的Python库

原文标题：

An Introduction to Recurrent Neural Networks for Beginners

原文链接：

https://victorzhou.com/blog/intro-to-rnns/

编辑：于腾凯

校对：杨学俊

译者简介

王雨桐，UIUC统计学在读硕士，本科统计专业，目前专注于Coding技能的提升。理论到应用的转换中，敬畏数据，持续进化。

翻译组招募信息

工作内容：需要一颗细致的心，将选取好的外文文章翻译成流畅的中文。如果你是数据科学/统计学/计算机类的留学生，或在海外从事相关工作，或对自己外语水平有信心的朋友欢迎加入翻译小组。

你能得到：定期的翻译培训提高志愿者的翻译水平，提高对于数据科学前沿的认知，海外的朋友可以和国内技术应用发展保持联系，THU数据派产学研的背景为志愿者带来好的发展机遇。

其他福利：来自于名企的数据科学工作者，北大清华以及海外等名校学生他们都将成为你在翻译小组的伙伴。

点击文末“阅读原文”加入数据派团队~

点击“阅读原文”拥抱组织