基于RBF神经网络的非线性系统识别（Matlab代码实现）

欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

1 概述

在此仿真中，实现了用于非线性系统的零阶近似的RBF-NN。模拟包括蒙特卡罗模拟设置和 RBF NN 代码。对于系统估计，使用具有固定中心和扩散的高斯核。而 RBF-NN 的权重和偏差使用基于梯度下降的自适应学习算法进行优化。

2 运行结果

部分代码：

    % Random initialization of the RBF weights/bias
    W1  = randn(1,n1);
    b   = randn();

    for k=1:epochs
        
        for i1=1:len
            % Calculating the kernel matrix
            for i2=1:n1
                % Euclidean Distance / Gaussian Kernel
                ED(i1,i2)=exp((-(norm(x(i1)-c(i2))^2))/beeta^2);
            end
            
            % Output of the RBF
            y(i1)=W1*ED(i1,:)'+b;
            
            % Desired output + noise/disturbance of measurement
            d(i1)= h(1)*x(i1+2) +h(2)*x(i1+1)+h(3)*x(i1)+h(4)*(cos(h(5)*x(i1+2)) +exp(-abs(x(i1+2))))+sqrt(noise_var)*randn();
            
            % Instantaneous error of estimation
            e(i1)=d(i1)-y(i1);
           
            % Gradient Descent-based adaptive learning (Training)
            W1=W1+learning_rate*e(i1)*ED(i1,:);
            b=b+learning_rate*e(i1);
            
        end
        
        MSE_epoch(k) = mse(e);  % Objective Function (to be minimized)
        
    end
    
    MSE_train=MSE_train+MSE_epoch; % accumulating MSE of each epoch
    epoch_W1=epoch_W1 + W1;        % accumulating weights
    epoch_b=epoch_b + b;           % accumulating bias
    
end

MSE_train=MSE_train./runs;  % Final training MSE after #runs of independent simulations
W1=epoch_W1./runs;          % Final Weights after #runs of independent simulations
b=epoch_b./runs;            % Final bias after #runs of independent simulations

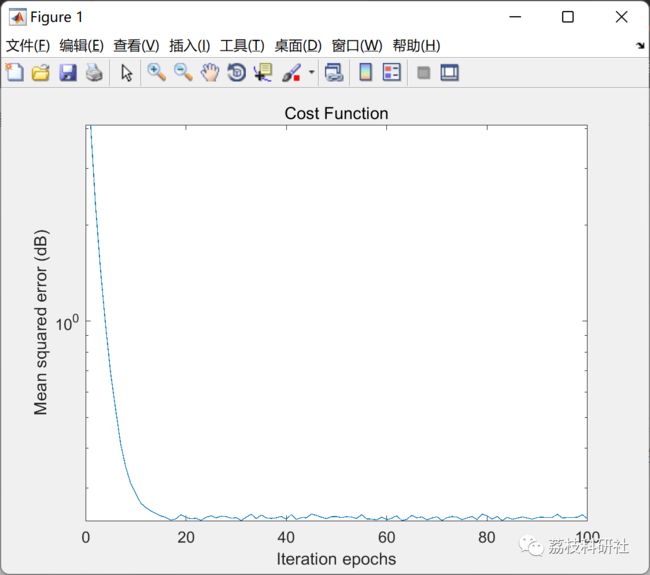
semilogy(MSE_train);    % MSE learning curve
xlabel('Iteration epochs');
ylabel('Mean squared error (dB)');
title('Cost Function')

Final_MSE_train=10*log10(MSE_train(end)); % Final MSE value

%% Test Phase
% Reset input and output
y=0;
d=0;
x=0;
x=[-1*ones(1,delays) ones(1,round(len/4)) -ones(1,round(len/4)) ones(1,round(len/4)) -ones(1,round(len/4))];
x=awgn(x,20);

for i1=1:len
    for i2=1:n1
        ED(i1,i2)=exp((-(norm(x(i1)-c(i2))^2))/beeta^2);
    end
    y(i1)=W1*ED(i1,:)'+b;
    d(i1)= h(1)*x(i1+2) +h(2)*x(i1+1)+h(3)*x(i1)+h(4)*(cos(h(5)*x(i1+2)) +exp(-abs(x(i1+2))));
    e(i1)=d(i1)-y(i1);
end
   
MSE_test=10*log10(mse(e));   %%% Objective Function

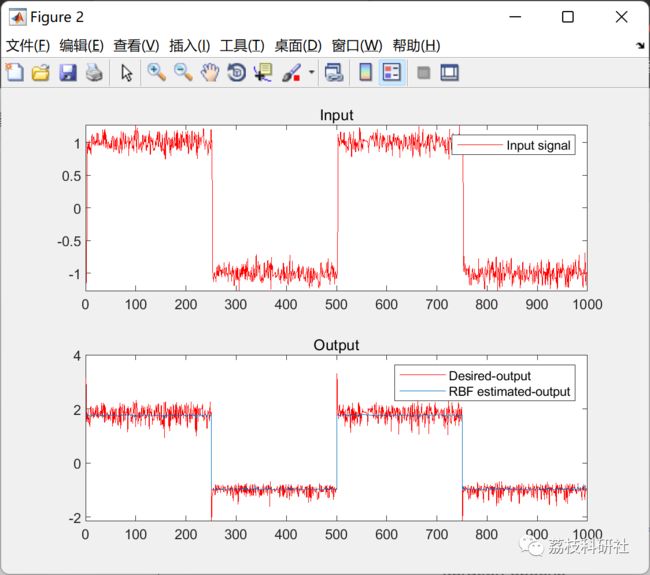
figure
subplot(2,1,1)
plot(x(1:end-delays),'r')
title('Input');
legend('Input signal')

subplot(2,1,2)
plot(d(1:end-delays),'r')
hold on
plot(y(delays+1:end))
title('Output');
legend('Desired-output','RBF estimated-output')

3 参考文献

[1]Khan, S., Naseem, I., Togneri, R. et al. Circuits Syst Signal Process (2017) 36: 1639. doi:10.1007/s00034-016-0375-7

4 Matlab代码实现