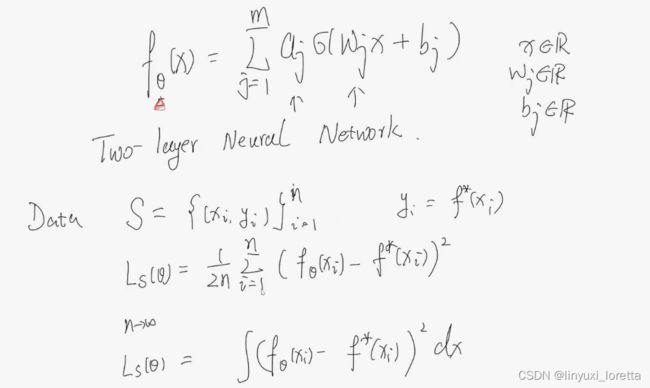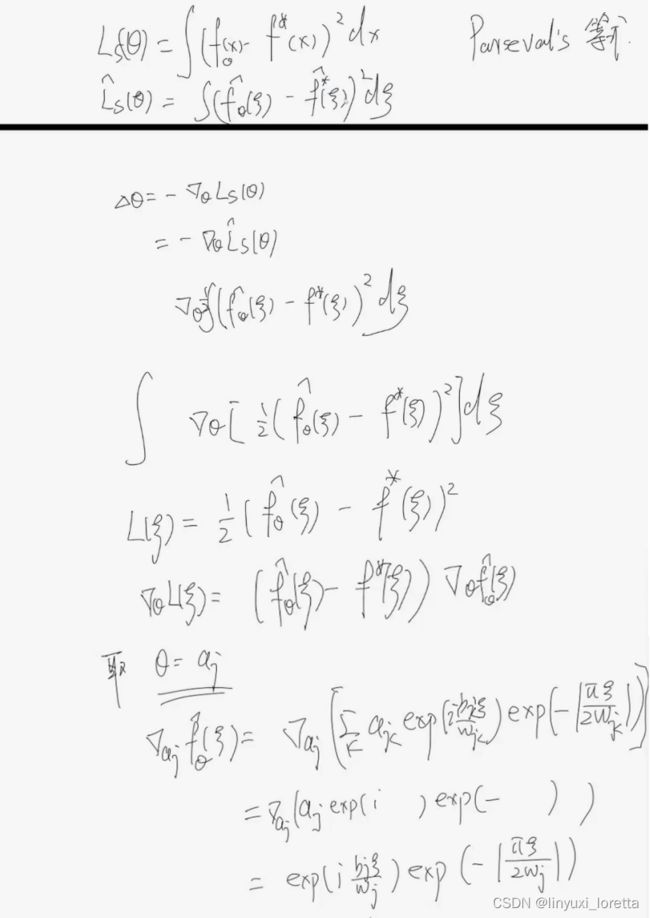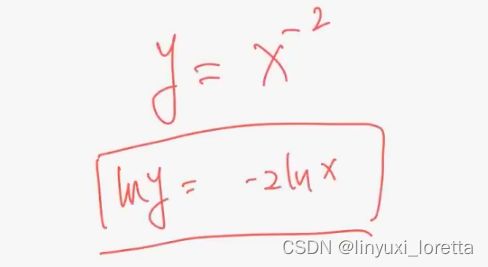2022人工智能数学基础2（交大许老师

参数量>>数据量    过参数化

限制条件没法完全限制住参数，多解

神经网络为什么好，应用的数据  图片、语言、文字这些数据很有价值

 

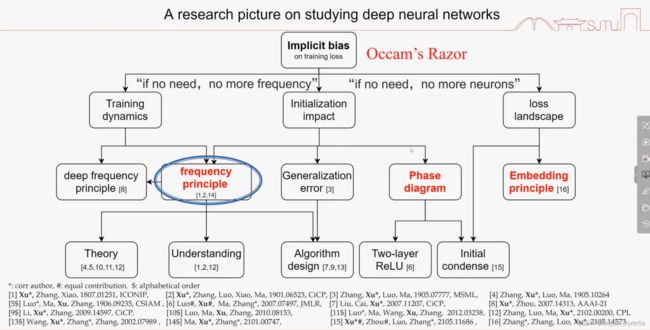
训练过程似乎遵循某些基本原则，叫“隐式正则化 ”  隐式偏向（人的意识里）

 

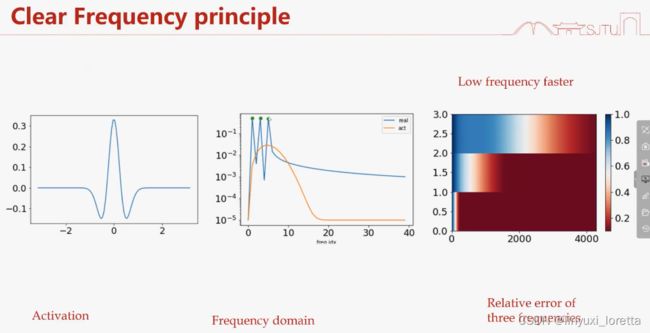
为什么偏向先学习低频？

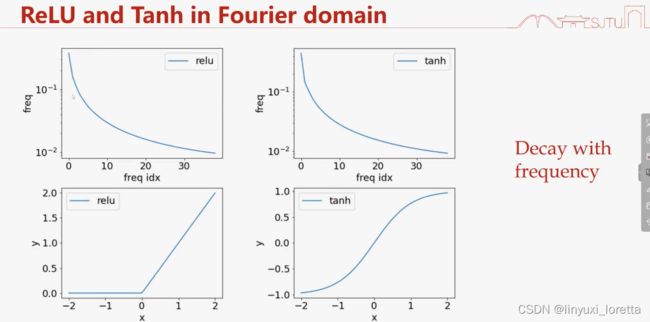
ReLU关于ξ^2衰减

函数积分后更光滑；光滑则衰减更快；频率空间和时域空间无法同时精确

光滑性就是看能否求导、是否连续

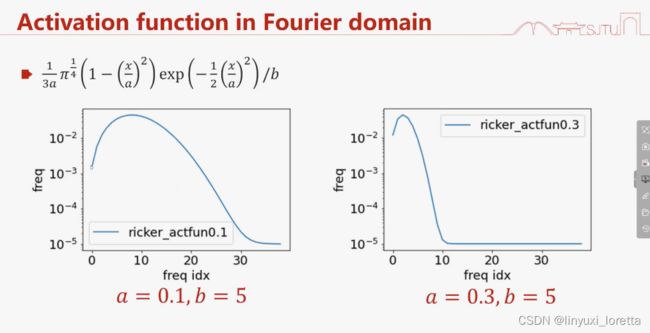
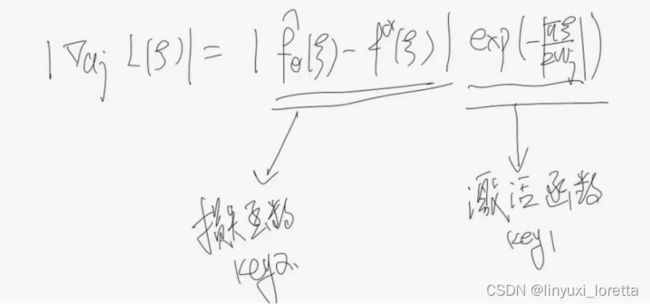
 激活函数 在傅里叶空间  单调衰减、和神经网络在傅里叶空间具有某种单调性 是一致的。

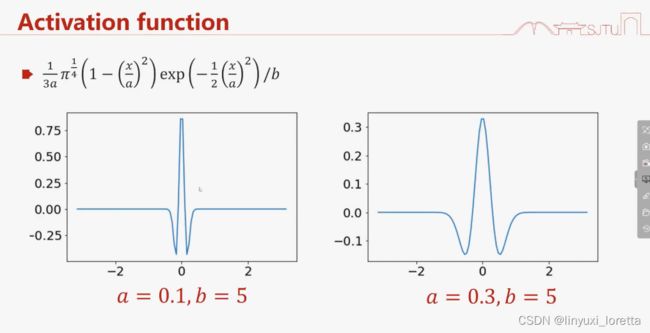
 二次函数*高斯函数

 

震荡越厉害，高频越多

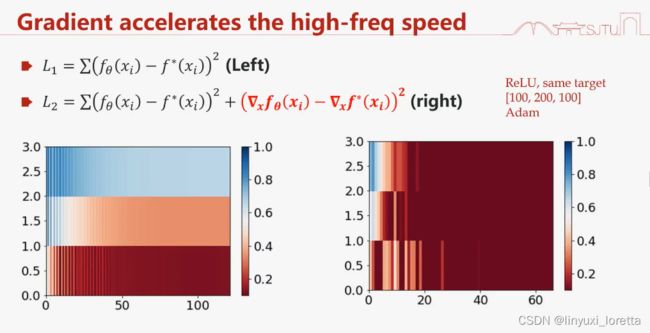
 加速高频的收敛

 

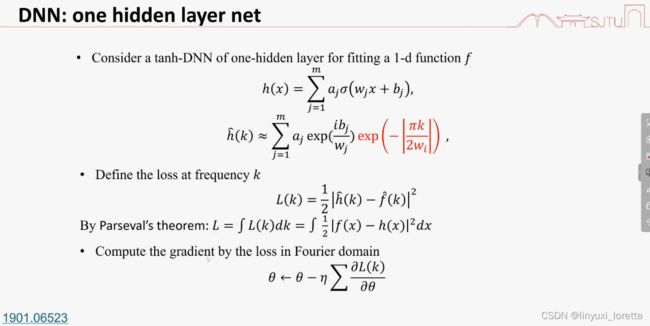
以两层神经网络为例：

 连续化以后  相对于考虑这两个函数的二范数

傅里叶变换是线性变换，求和不变

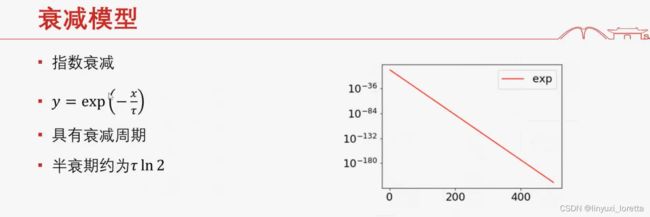
   无穷光滑，无穷快的衰减，指数衰减

 

 

 激活函数的光滑性正则性，通过链式法则，影响了函数在傅里叶空间里的衰减速度。

 

要做泰勒展开，需要x和x0靠近。

 

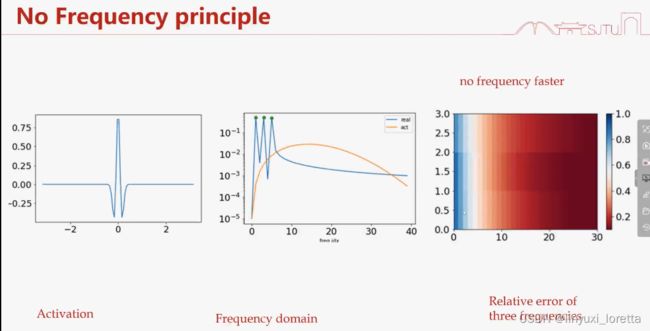
实作上，有些高频成分收敛的实在太慢了，用稍微不光滑的激活函数比如Relu，速度就会快很多

 

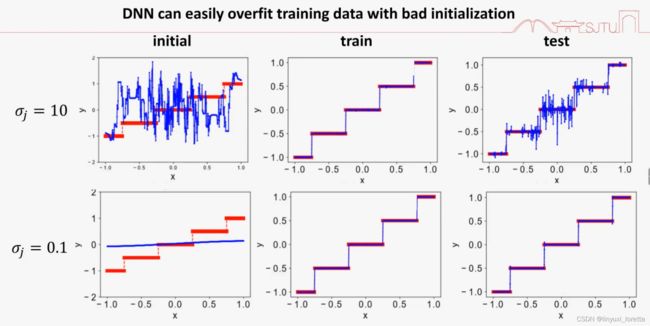
w很大时， f(wx)会变得很shock、剧烈震荡、有很多高频成分

结论：初始化很大，泛化性差。

 

共轭梯度下降算法、truncated牛顿算法、BFGS、粒子群算法（不用梯度信息）、蒙特卡洛，等算法都可以观察到低频先收敛的现象。

采样里有噪音、测试集和训练集分布不完全一样，

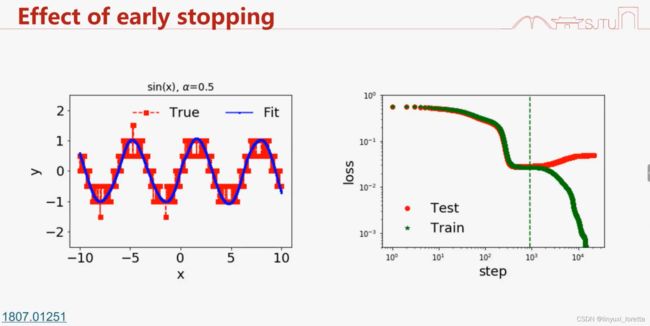
1 .提前停止会有效，前提：数据是低频，噪音是高频

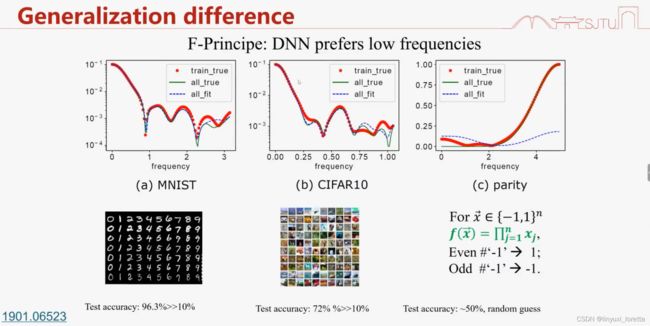
 2.奇偶函数 神经网络泛化性很差，随着频率增加、幅度变大，奇偶函数任意变一个量，输出就发生了变化，输出对输入的敏感程度很高，就叫高频（反应变化程度）。

图像识别这类问题 神经网络泛化性很好。因为高频幅度很小，不影响

（c） 采样时会加入一些额外的高频杂讯，

高频占优的函数下，泛化就非常糟糕。

微分方程本质上就是一个方程  里面含有导数，

函数到函数的映射就叫算子，解一类方程

 

判断函数是否简单，频率不高

高频问题有时候是很重要的，地震波、电磁波

解高频问题实际上是很容易的，

二次导问题，可以离散化的形式、差分的形式，去逼近导数。中心差分，本质来讲就是泰勒展开。变成解线性方程组问题，矩阵很大时，很困难，用传统算法 jacobi迭代，高频收敛特别快，会遇到光滑性问题，低频很难学。

所以可以和神经网络结合。

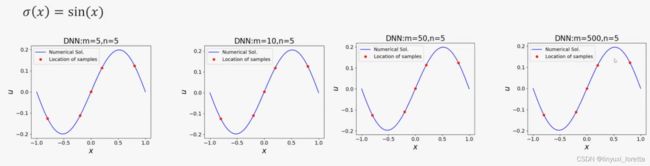
谱方法，相当于sinx做激活函数，传统方法学 菱角分明，

relu   神经网络学 变光滑了，因为有低频倾向

 

 

当函数高时，神经网络学起来困难，把高频变低频：

拉伸

 g(x) =f(wx)   w>1    不同方向不同拉伸 “凑”...

算子。作用：神经网络有时候训练很难，有个高手都调好，解PDE就查表，再配上蒙特卡洛积分，工业上用差不多了，只要精度不是要求很高

 

找到可参数化的优化函数，有目标，就可以做神经网络，

非线性就套非线性的激活函数

神经网络参数太多了  解方程很难，就用梯度下降找0点。

牛顿法本质上就是找一阶导的0点。

---

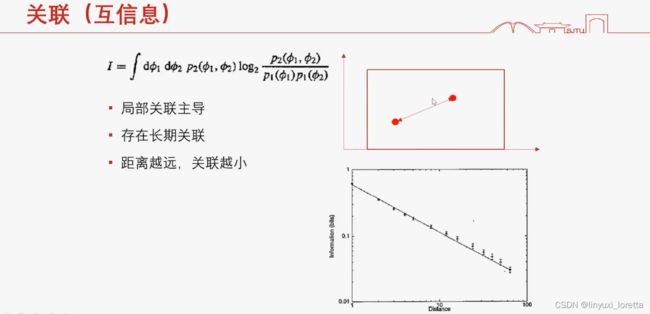
损失函数， p代表每一点上的概率，q代表另外一个分布，这两个分布一个在log里一个在log外，不可交换，含义：用pi编码qi，平均能编码多少，用pi分布逼近qi

 

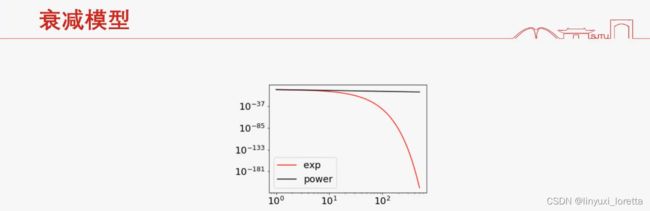
  数据在傅里叶空间有衰减特性， ln2通常称为时间尺度

PDE

 

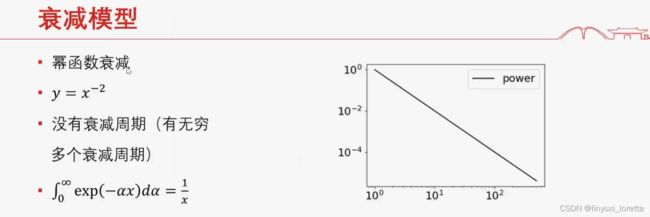
没有固定时间尺度

 loglog画图

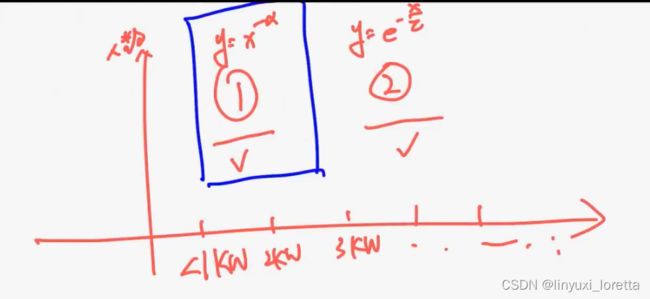
 两个小游戏

 有各种周期时，求和就是幂衰减。周期很大 需要衰减很久，长尾效应

网页指向模型、财务聚集模型

这是 描述数据特征的重要方法

 图片的衰减特性 幂律衰减 ，高频不多但存在，

 

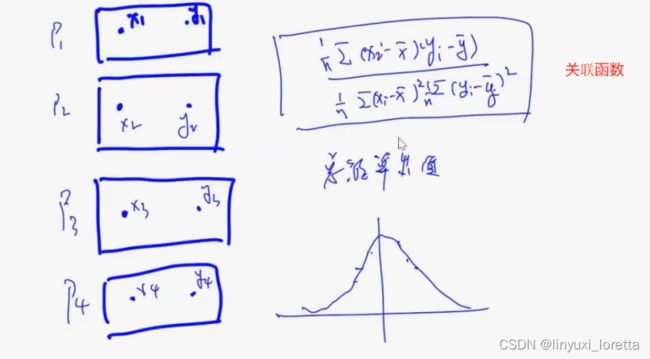
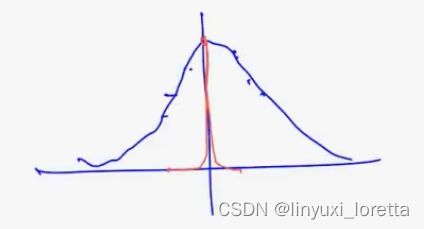
采多少样本都很难判断均值为0，只能大致判断量级，

 

如果方差很小 采几个样本就能算方差了

 想要一个误差10^(-3)，需要10^6 一百万张图，

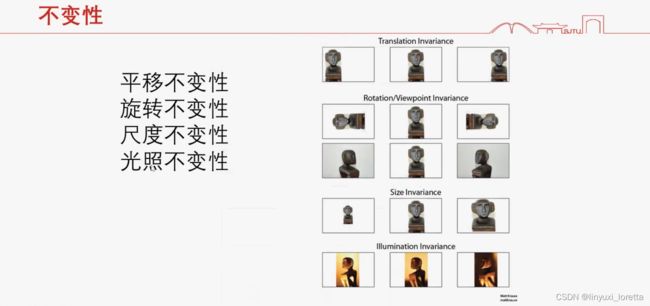
以上 是图片数据的特征不变性、衰减、关联。

图片分类问题困难在这。

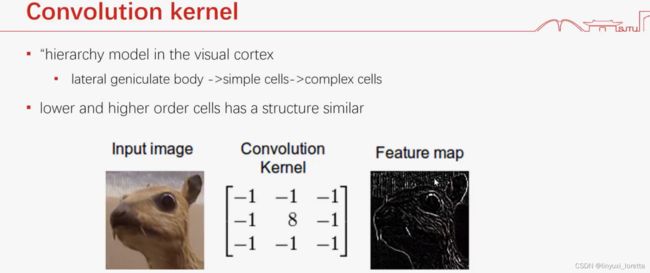
时域的卷积=频域的乘积

这个kernel 加起来=0，保留变化大的地方，边界上保留一些非0元素

sharpen相同的不消掉，锐化

 

可以加个t，比如t很小，0.001 ，可以让p间的距离变大，调参