一种基于卷积神经网络的图像去雾研究-含matlab代码
目录
- 一、绪论
- 二、去雾卷积网络
-
- 2.1 特征提取
- 2.2 多尺度映射
- 2.3 局部均值
- 2.4 非线性回归
- 三、实验与分析
- 四、Matlab代码获取
一、绪论
雾是一种常见的大气现象，空气中悬浮的水滴、灰尘、细沙或其他颗粒等都会引起成像清晰度的降低。单幅图像去雾是一个病态问题，其关键是如何准确地估计成像过程中的大气透射率。现有的图像去雾方法普遍利用基于观察经验的先验知识来构建去雾模型。近几年，机器学习方法被逐步应用于图像去雾的研究中。
众所周知，人类的大脑可以在无附加信息的条件下从单个自然场景中迅速地识别出有雾区域。近几年，生物启发式的卷积神经网络在高层次视觉任务已取得成功的应用，如：图像分类、人脸识别、物体检测等。基于卷积神经网络的深度学习方法也开始逐步被应用于图像修复等低层次视觉任务。然而，现有的网络结构并不能被直接应用于单幅图像去雾。
二、去雾卷积网络
有雾图像的描述模型为：
I ( x ) = J ( x ) ∙ t ( x ) + A ( 1 − t ( x ) ) I\left( x \right)=J\left( x \right)\bullet t\left( x \right)+A\left( 1-t\left( x \right) \right) I(x)=J(x)∙t(x)+A(1−t(x))
其中，I是实际观测的图像；J是没有雾情况下的理想场景图像，它仅与地物相关；A是大气的光亮度，图像去雾的实质是恢复从单幅图像Ⅰ恢复J和A；t是大气介质透射率，它与大气的厚度紧密相关，因而随像素的位置而变化。大气散射模型指出透射率估计是重构清晰图像的关键。
去雾卷积网络的网络结构由卷积、池化和非线性函数共同组成4个连续的操作层实现透射率估计，分别是：特征提取、多尺度映射、局部极值和非线性回归。其中，包含了3个卷积、1个最大池化、最大输出单元和BReLU激活函数。
2.1 特征提取
为解决图像去雾这一病态问题，传统去雾方法基于先验假设在输入图像中密集地提取与雾相关的特征，如：暗通道（Dark Channel）、色相差异（Hue Disparity）、颜色衰减（Color Attuation）等。注意到，密集的特征提取可等价于线性的卷积操作和独特的非线性映射。因此，受经典先验特征中颜色通道极值的启发， DehazeNet采用独特的激活函数——最大输出（Maxout）单元用于非线性映射与特征降维。Maxout单元是一种简单的前馈非线性激活函数，常用于多层感知机（Multilayer Perceptron，MLP）和卷积神经网络（Convolutional Neural Network， CNN）。当应用于CNN时，Maxout单元将输入特征图的k个通道分为一组，分别对各组执行像素级的最大值操作。基于“卷积+Maxout”， DehazeNet 第一层的特征提取可表示为：
其中， W 1 {{W}_{1}} W1和 B 1 {{B}_{1}} B1分别表示滤波器的权值和偏置，*表示卷积操作。
是k ×n1个f1×f1的卷积滤波器，其中3是输入图像的通道数。 Maxout 单元映射 kn1维的卷积结果并输出 n1 维的特征图，取代传统先验特征实现自动化的雾相关特征提取。
2.2 多尺度映射
在前期去雾工作中，多尺度特征被证明在图像修复中的有效性。多尺度特征不仅可刻画不同尺度的物体，还可有效地应对物体的尺度变化。例如， GoogLeNet中的inception结构并联多个不同尺度的滤波器，解决了图片分类中物体的尺度对齐问题，并在 ILSVRC14中取得最好效果。受多尺度特征提取的启发，在第二层结构中并联三组个数相同、尺度不同的卷积操作，滤波器尺度包括3×3、5×5 和7×7。数学形式上，该第二层的多尺度映射可表示为：
F 2 i = W 2 [ i / 3 ] , ( i \ 3 ) ∗ F 1 + B 2 [ i / 3 ] , ( i \ 3 ) F_{2}^{i}=W_{2}^{\left[ {i}/{3}\; \right],(i\backslash 3)}*{{F}_{1}}+B_{2}^{\left[ {i}/{3}\; \right],(i\backslash 3)} F2i=W2[i/3],(i\3)∗F1+B2[i/3],(i\3)
W 2 {{W}_{2}} W2和 B 2 {{B}_{2}} B2分别包含n2个可分解为3组的权值和偏置。其中，n2是第二层网络的输出，i∈[1, n2]是输出特征图的索引，⌈·⌉表示向上取整，\表示取余操作。
2.3 局部均值
为获取空间不变性，视皮层复杂细胞对简单细胞的响应进行非线性的特征整合。Ilan等人提出复杂细胞的空间整合机理可描述为一系列的池化操作。根据CNN的经典结构，邻近像素间的局部最大值操作可增强特征空间变化的鲁棒性。此外，局部极值操作符合透射率的局部一致性假设，此假设被普遍地应用于透射率的估计误差消除。因此，局部极值操作为去雾卷积网络的第三层，表示为：
其中， Ω (x) 是以 x 为中心的f3×f3邻域，第三层特征的输出维度 n3 = n2。不同于标准卷积网络中最大池化降低特征图的分辨率，局部极值操作是最大值滤波器，其密集地应用于特征图中的每个像素点，因此更好地保持了图像的细节分辨率。
2.4 非线性回归
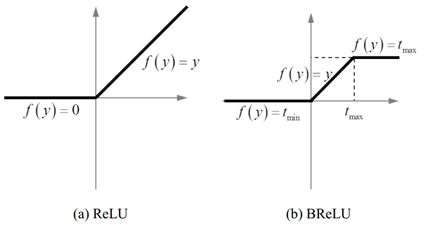
在深度学习中，常用的非线性激活函数主要包括：Sigmoid 函数和修正线性单元（Rectified Linear Unit， ReLU）。Sigmoid 函数由于两端的响应饱和，容易出现梯度弥散现象，并可能导致网络收敛缓慢或陷入局部最优解。为解决梯度弥散的问题，ReLU提供了稀疏的特征响应。然而，ReLU的提出主要针对图像识别的分类问题，而非图像重构的回归问题。 ReLU 的输出只抑制了小于 0 的值，这可能会导致响应溢出，特别是图像重构问题中 [0, 1] 的有限响应输出。为了解决响应溢出的问题，采用双边修正线性单元（Bilateral Rectified Linear Unit， BReLU），如下图所示：
BReLU是一种新的激活函数，既保持双边修正又保证局部线性。基于 BReLU，输出层可定义为：
其中， W4 ={W4} 包含一个尺度为 n3×f4×f4 的滤波器， B4 = {B4} 是其偏置， tmin;max是BReLU的修正边界（文中tmin=0，tmax=1）。根据上式， BReLU 激活函数的梯度可表示为
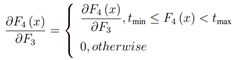
三、实验与分析
基于卷积神经网络的图像去雾结果如下图所示，去雾效果明显。
四、Matlab代码获取
上述matlab代码可私信博主。
博主简介：擅长智能优化算法、信号处理、图像处理、机器视觉、神经网络等领域Matlab仿真以及实验数据分析等，matlab代码问题、商业合作、课题选题与指导等均可私信交流。