严正安

半导体器件物理 2022.10.13

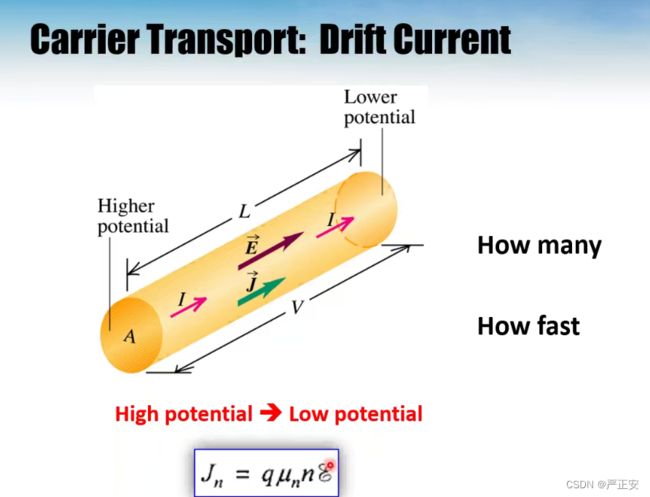
漂移电流由两部分组成

扩散电流

扩散电流+漂移电流就是总的电流，在实际问题中漂移电流远远大于扩散电流

空间电荷限制电流，对于本征半导体和一些绝缘体里面的电流，我们的作业

我们首先忽略我们的扩散电流，只考虑扩散电流

电流密度不随位置变化而变化

电流密度和电场的乘积是不变的，靠近输入端，电场强度大，载流子浓度小，

枪声一响，选手就进入正式的赛到，刚开始的时候，因为前面是空的，所以跑起来会快一些，后面的人因为人挤人所以会比较慢，靠近电流输入端，浓度高，这些空间电荷是从输入端的电极注入进来的

空间电荷来自输入端电极大量注入的载流子，载流子并不是来自于本来的半导体中的，本征的载流子是很少的，来自于输入端电极里的，就像一开跑，所有人涌进来，原来的赛道是中性的，由于电子注入大量的载流子，这些注入进来的，就变成了净电荷，他们既是载流子也是多出来的净电荷，由于高斯定理，就会产生场强，电荷会产生分布，达到稳态的时候， $\small n(x)$ 靠近电流输入端的时候多，在载流子多的时候大家看一下推导过程，那个位置的局部场强就会笑，但是 $\small n(x) \times E(x)$ 就是不变的

但是往 $\small n(x)$ 靠近的时候，载流子越少，局部场强越大， $\small n(x) \times E(x)$ 就会一直保持常量，直到电极的另一端，这是物理上的理解，上述图片是数学上的推导，再进阶一点，就是希望大家可以我们怎么理解，上述涉及的过程，有一些比较简单的载流子，这些半导体也是中性的，这是欧姆定律，大家也可以理解的

J正比于V的平方，它的物理根源来自于电极，不是来自于半导体，由于空间电荷不是均匀分布，这就有别于欧姆定律的情况，再根据我们的推导。我们就可以得到一个理论结果，我们就知道不再正比于电压，它与厚度，电压都有关系

2.载流子的注入是比较容易地，注入的这一端是欧姆接触，进来很容易（不像其他同学猜想的那样），我们在推到的时候，没有考虑注入的障碍

陷阱态和迁移率会不会有变化？

实际上整个过程假设迁移率不随空间变化而变化，我们用迁移率指的是自由载流子的迁移率，他不涉及到陷阱态，我们不考虑缺陷。否则就会变得复杂，迁移率会受到陷阱态的影响，我们的迁移率，指的就是自由载流子的迁移率，事实上，一直到今天，很多文献也在研究，不同的陷阱态对SCLC的影响（比如非晶的半导体，有机的半导体），在那种复杂情况下J会正比于 $v^{\alpha} ,\alpha>=2$ ,有陷阱态的时候 $\alpha>2$ ，L的三次方也会有所增加，这和陷阱态的分布有关

我们要求大家掌握的就是理想情况下，不存在势垒什么的，本征半导体和绝缘体之间，就是一个自由载流子，从电极注入进来的都是自由载流子，

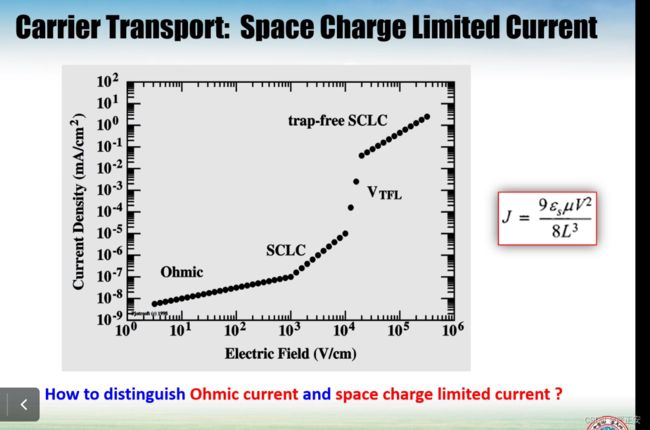
我们来分析观察实验现象，我们看这个例子，横坐标已经把电压换算成电场了

横坐标就是指数坐标的电压，纵坐标就是电流密度，它刚开始有一段横纵坐标都是指数坐标的情况下，有一段写的是Ohmic，SCLC空间电荷限制电流，电场相对比较大的时候，会出现

怎么区分欧姆电流和空间电荷限制电流？

斜率和几次幂相关，空间电荷限制电流是二次的，而欧姆定律是一次的

为什么在电压小的时候，J正比于V？

输入端电压小，注入的载流子少，以本征的为主

SCLC的本质是来自于电极的大量载流子

本征半导体中有一个比较深的能级，上面有一些陷阱态，目前是空的，当载流子大量涌入之后，就会填充深陷阱态，填充之后，就会有大幅度提升，之后，填充满了，就不有大幅度的提升，此时的SCLC的就是我们推导的自由载流子

这两段都符合，但是会出现 $\mu$ 之间的差异，所以会出现区别

我们会用到SCLC的概念，也会用到其他的一些东西

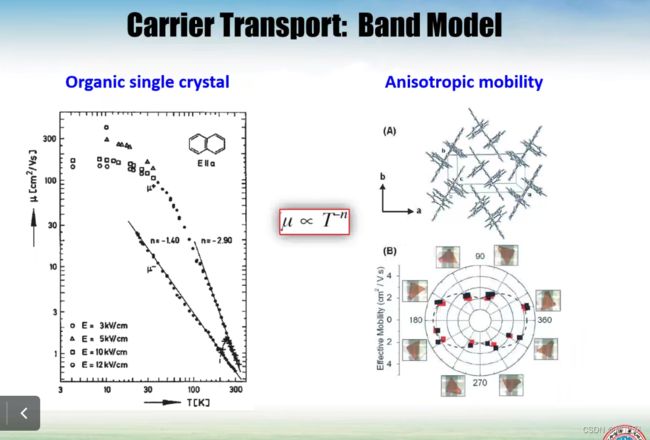
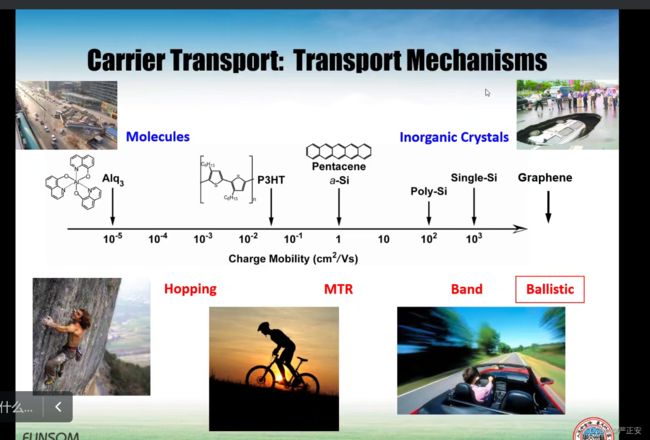
我们首先讲的Si的单晶还有一些绝大部分无机半导体的单晶还有一些有机半导体单晶

物理模型用的就是能带输运模型，我的载流子是在一个导带，完全离域的energy band里面，这种的它的这个特点是随着温度的增加，它的迁移率反而是下降，温度越低，迁移率越高，输运的越快

我们基于能带输运的模型，离域的载流子主要受晶格散射的影响，晶格格子的振动加强，所以在低温下，平均加油程更长，这就是离域能带输运最典型的特征

从定性上理解，Band transport 的特征

右手边的这个图，Anisotropic mobility 各向异性的迁移率，在有机中特别普遍，根源是因为有机分子，不会是一个球形对称的，不像无机分子，有机都是有构型的，有各种各样的构型，各种形状都有，这种构型会造成晶格，他就会造成在不同的方向，电子云之间交叠的程度，差别非常大，导致，电子云交叠比较多的方向，载流子输运更加像能带式的输运，如果没有交叠，就好像要从一个跳到另一个，这个方向的迁移率就会产生数量级的差别

比如多晶或者非晶的半导体薄膜，像多晶硅，特别是对于非晶来说，Armorphous Solid，它里面的能带结构，已经不再是离域的能带，不再是energy band，每一个地方，处处都是缺陷（因为是非晶），每一个空间位置，能级位置处处可能会产生差异，我们不能用能带去描述，我们用localized state，我们用局域电子态来描述，局域电子态所组成的物理图像，以前我们画能带的时候

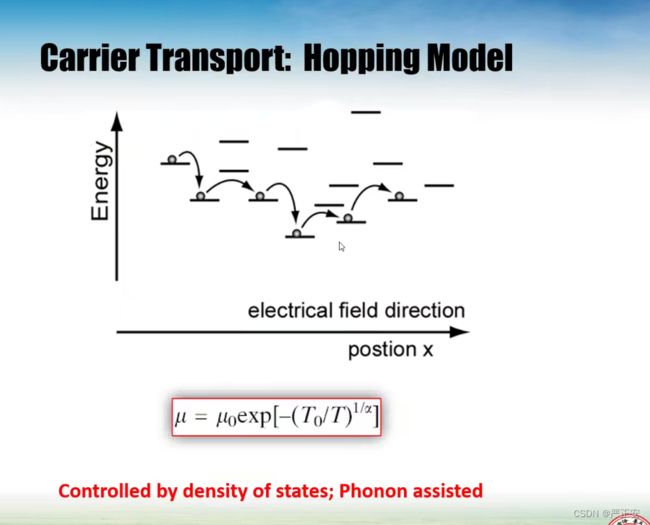
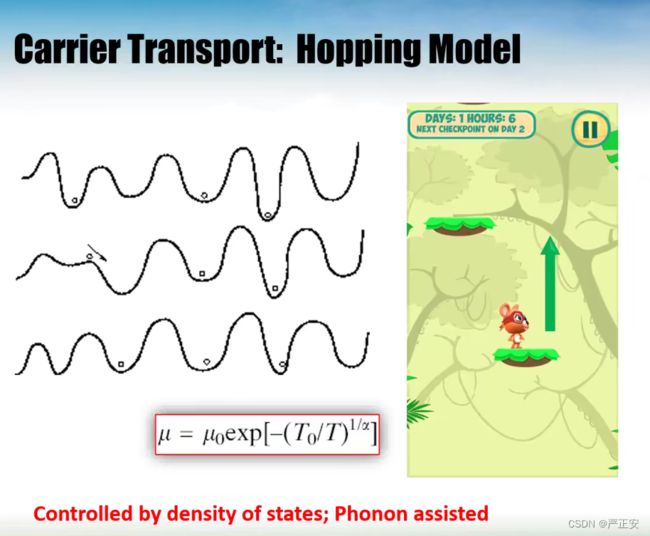
聚集了大量的局域电子态，画了很多短线，原先是在大马路里面跑，它也可以定向输运，载流子跳跃的概率从左往右大于从右往左，但是还是比原先的要低很多，我们称作Hopping Model，叫做Hopping among localized states

要实现产生电流的运动，某个能级要有大量的局域电子态，另外一个他们都是局域的，这就是一个很典型的Hopping Model

从一个局域跳到另一个局域，需要声子，来自晶格振动的某一个量子化的能量，就有可能帮助我实现跳跃

解释：

每一个坑看作局域电子态，位于坑里面，困在这个里面，需要某一种方式获得能量，我们有一定的跃迁几率进行跳跃，但是我们还有另外一种情况，晶格振动使得能量发生一些变化，受到声子的影响，势能比平时高，这样就有可能滚到下一个能级上去，这一种模式就比较像Hopping

两个局域电子态的能量差别就好像超级玛丽中平台的移动，一旦满足要求，就会进行移动，在近的时候，载流子从一个局域电子态Hopping到另一个电子态的机率就会增加

如果温度越高，这个载流子就可以跳的更高，Hopping就会得到增强

这个就有Band Model相反

温度越高，载流子获得热能跃迁的概率就会越高，所以局域电子态之间的成功率会更高

如果电子态的密度越高，通常情况下也会更加容易发生Hopping

只要是Hopping model 它在数量级上会低于我们原先的Band Model

极化子模型

最简单的极化子就是偶极子，一个偶极子就可以看作式Polaron

那么比如说一个极性分子，正负电荷中心不重合，可以看作偶极子

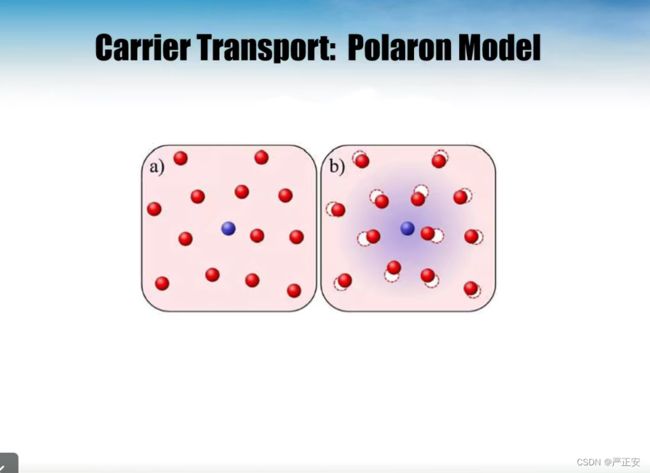
比如说在晶格里面，红色代表格点，蓝色代表载流子，红色这些格点上可能没有，对于大部分极性的无极分子，如果说我在某个格点上有，蓝色可以看作式空间电荷，蓝色的会使周围的格点发生极化，当然离得远的，就会受到小的影响，主要对近邻的产生影响，产生趋近于中心的一个极化

如果把载流子和它周围的极化区域看作一个整体，就可以看作是极化子

一旦带电，周围的场就会不一样

为什么极化场这么重要？

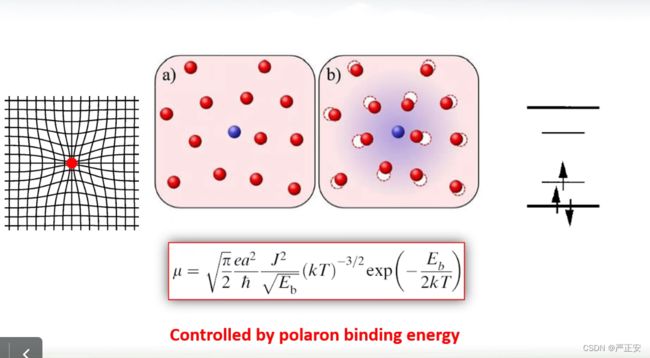
因为极化场会反过来影响载流子本身

极化子对场的影响在于binding erergy

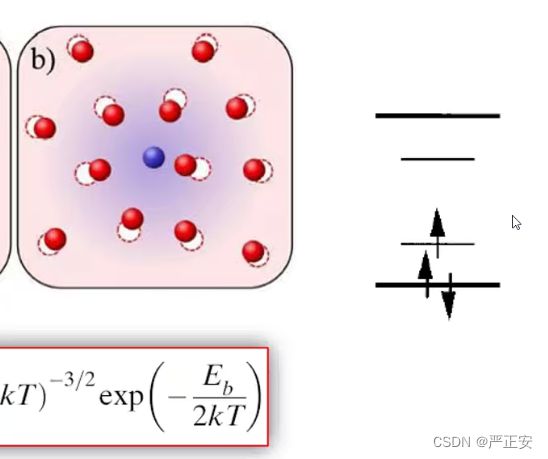
最低的分子的空轨道，上面是最高的占据轨道，如果没有极化场，电子就在最低的空轨道（粗的黑线上运动），如果有极化场，极化场就会改变这个轨道的势能，跑到更细的实线上，，能量的差别由极化场带来的，最高占据态的上方，也会引入电子态，如果极化子要从格点移动到另外一个格点，他是要克服binding energy，他首先要跳过去，它在跳回到西线的位置上，每一次运动都要克服Binding erergy

激子也有结合能，excition binding erergy

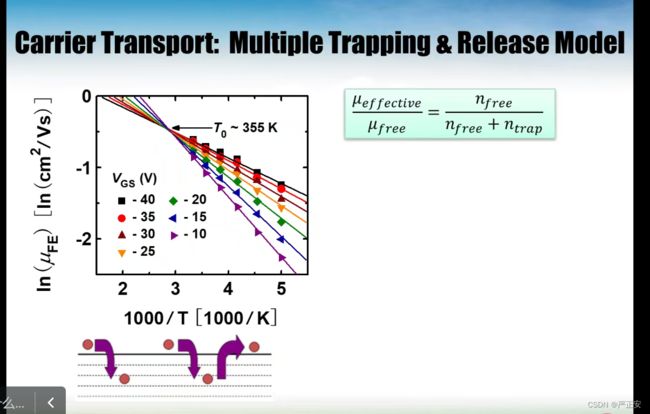
这个载流子输运的模型，我们会有一些定量化的要求，最早是在非晶硅的晶体管里面，提出物理模型

这个物理模型基于这样的假设，单晶的陷阱态很少的时候，就是能带输运，但是因为非晶膜和多晶薄膜，在带隙中存在大量的陷阱态，假设有很多的陷阱态，电子在导带上输运的时候，大部分会掉到这个坑里面，达到稳态的时候，大部分的电子是在陷阱态里面，还有少部分在导带上，这个时候就达到了一种稳态，不随时间变化而变化

那我怎么来描述迁移率？

实际上里面有一些载流子式移动的，有一些是不动的，可以计算出自由载流子的迁移率，电流测量出来的是等效迁移率，有100辆车，90辆在开，但是我们算的是100辆的平均速度

动和不动的看作一个整体，因为这是我们测量出来的

我们又可以计算出动的那部分载流子的迁移率

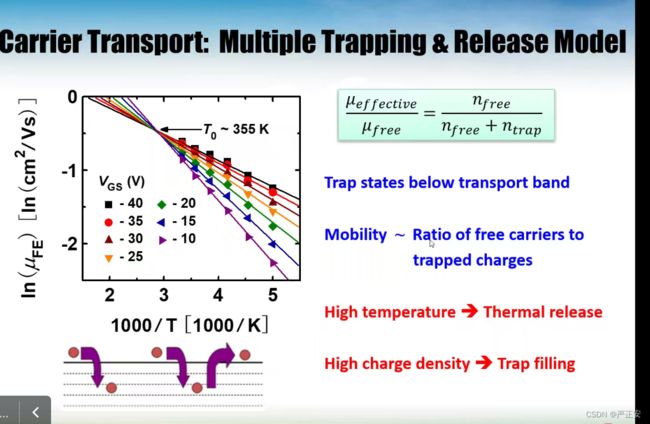
逃离陷阱的过程，一般就用 thermal release

当有外加电场，导带上的可移动电子肯定会定向移动，进入坑，爬起来，反复的这么一个过程

我们要叫做 MTR模型

我们通常情况下

如果trap 远远大于free ，上方这个公司就可以近似成 $\frac{n_{free}}{n_{trap}}$

和hopping有点像，温度越高，上述比例取决于

1.陷阱态的数量

2.温度

两个典型的变化

1.随着温度增加，迁移率增加

2.温度上升会趋近于一个常数，也就是自由载流子迁移常数

提前放出作业

single 指的是一个能级上有陷阱态

首先用MTR model,我们要计算的是，推导出在这种情况下，等效电子迁移率的表达式，刚才我们的slide 讲的是要用这个公式，比例究竟是什么，取决于陷阱态的数量和分布，我们把数量和分布给他大家，推导出 $\mu_{effective}$ 究竟等于什么

我们知道导带价带的位置，费米能级的位置也是知道的，我们只考虑在某一个特定的能量上， $\mu_{t}$ 上有一些深陷阱态，密度也是知道的，然后，我们导带上的 $\mu_{free}$ 也是知道的,我们要求 $\mu_{effective}$

不仅要把结果式写一下，而且要有解释的过程

我们针对的是N型半导体，进阶的话，我们可以考虑一下对于P型半导体

这个表是来自于教材

在绝缘体里面，它的一些导电过程，你去看左边的这个过程，有隧穿，热电子发射，

你如果看到一个复杂的物理表达式，我们并不需要记住每一个数量，我们只需要关键物理参数的依赖性，右手边就是非常好的例子，电压依赖性和温度依赖性，和不同的传输机制，不同的机制经常会有对应不同的电压依赖性和温度依赖性，这有助于我们理解它的机制，它跟我们的测量是有关系的，我们从理论上分析，和从实验上进行测量分析

如果有e指数，外面有平方，里面也有平方，v指数依赖性更强，你会看出来，当他的电压变大的时候，根据隧穿的电流，有什么变化？

隧穿电流的解释，他为什么会穿过去？

隧穿的本质在于电子也是物质波，有波的性质，当障碍物小雨波长的时候，有一定的概率可以穿过去，和温度没什么关系，不是靠热激发翻过势垒

热电子发射，就好比是翻过这个势垒，V实际上是外加电压，我可以让V接近于0，要讨论里面系数的正负性，温度越高，越容易越过势垒，因为势垒在加了电压后会产生变化，所以变成根号

输运机理：

非晶的有机分子形成的薄膜迁移率非常非常低

Ballistic 弹道输运，就相当于几乎不受到晶格散射的影响，迁移率会高非常多

CX8903：Ebike自行车仪表电源方案开发,Ebike智能仪表电源芯片诚芯微科技社交电子
CX8903：电动Ebike自行车仪表电源方案开发,Ebike智能仪表电源芯片推荐。电动助力自行车EBIKE凭借其环保、健康、低噪、和便捷等特点，成为了越来越受欢迎的骑行便利交通工具。提供电动Ebike自行车仪表电源方案开发、E-BIKE电动助力自行车仪表供电电源解决方案。CX8903采用100V高压制造工艺（芯片最高耐压可到100V以上），SOP-8L贴片封装，CX8903内置100V/90mΩ
ARM驱动学习之基础小知识 JT灬新一 ARM 嵌入式 arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购（能不能买到，价格）–原理图（涉及到稳定性）•layout画板工程师–layout（封装、布局，布线，log）（涉及到稳定性）–焊接的一部分工作（调试阶段板子的焊接）•驱动工程师–驱动，原理图，layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案，原理图(网表)–layout工程师（gerber文件）–PCB板
希望和悲伤都是照亮我们人生的一缕光山月映雪
我开始并不想读《云边有个小卖部》，但看到好几个学生就都在读这本书，为了了解学生的阅读实际，我就拿起这本书翻看起来。读了十几页，发现小说的语言中不时有一些粗俗的字眼，感觉自己读不下去了。小说一开始把云边镇风景写的特别的美好，我错判为脱离现实的鸳鸯蝴蝶派小说，对于人为制造的童话世界的人与物，我真的不太感兴趣，所以就没有再读了。有天在教室闲转，顺手又拿起了这本书看了起来，这次我才真的看进去了。这部小说除
《度五行》生活报报甲午62：不通痛苦，太通也痛苦，要健康快乐，需要通体舒畅。 YangduSam2021
220809壬寅戊申甲午，《度.生活五行》:天干土克水，水生木，木克土。地支寅申冲，寅午合。20220809，周二，兴大上海六班2512天，西交大2013上海班3212天，后TA15332天，度生活619天，今天拜访了一家有趣且当红产业的新创公司AK。AK一开始从事深海新能源储存与供电设备的研发生产制造，2年前开始做移动与家庭储能设备的研发生产制造。觉得有趣是因为这是笔者认知里用科技做降维打击的公
(179)时序收敛---＞(29)时序收敛二九 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛二九（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）
(180)时序收敛---＞(30)时序收敛三十 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛三十（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）
(158)时序收敛---＞(08)时序收敛八 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛八（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(159)时序收敛---＞(09)时序收敛九 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛九（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(160)时序收敛---＞(10)时序收敛十 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛十（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(153)时序收敛---＞(03)时序收敛三 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛三（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(121)DAC接口---＞(006)基于FPGA实现DAC8811接口 FPGA系统设计指南针 FPGA接口开发(项目实战)fpga开发 FPGA IC
1目录（a）FPGA简介（b）IC简介（c）Verilog简介（d）基于FPGA实现DAC8811接口（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电
FPGA复位专题---（3）上电复位？ FPGA系统设计指南针 FPGA系统设计(内训)fpga开发
（3）上电复位？1目录（a）FPGA简介（b）Verilog简介（c）复位简介（d）上电复位？（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限
(182)时序收敛---＞(32)时序收敛三二 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛三二（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）
2025第十二届广州国际汽车零部件加工技术及汽车模具展览会 ws201907 人工智能大数据汽车
2025第十二届广州国际汽车零部件加工技术及汽车模具展览会时间：2025年11月20日-22日地点：广州保利世贸博览馆(PWTCExpo)预计20000平方米展出面积；400多家参展商：20000多名观众；汇集了各种汽车零部件成品、汽车模具以及机床加工技术的行业盛会；聚集超过80家汽车主机厂以及3000家一二级零部件制造商参观展览会！展会简介：2025第十二届广州国际汽车零部件加工技术及汽车模具展
助力新能源汽车产业发展，2025第五届广州国际新能源汽车产业智能制造技术展览会将于11月在广州召开 ws201907 制造汽车
助力新能源汽车产业发展，2025第五届广州国际新能源汽车产业智能制造技术展览会将于11月在广州召开伴随着全球新一轮科技革命和产业变革，汽车与能源、半导体、物联网等领域有关技术加速融合，新能源汽车已成为全球汽车产业转型升级的主要方向。近年来，在相关政策的影响下，新能源汽车市场呈现出快速增长的态势，市场规模不断扩大。截至2020年，中国新能源汽车保有量已超过500万辆，成为全球最大的新能源汽车市场。随
C++常见知识掌握 nfgo c++开发语言
1.Linux软件开发、调试与维护内核与系统结构Linux内核是操作系统的核心，负责管理硬件资源，提供系统服务，它是系统软件与硬件之间的桥梁。主要组成部分包括：进程管理：内核通过调度器分配CPU时间给各个进程，实现进程的创建、调度、终止等操作。使用进程描述符（task_struct）来存储进程信息，包括状态（就绪、运行、阻塞等）、优先级、内存映射等。内存管理：包括物理内存和虚拟内存管理。通过页表映
以研发创新为驱动力，黄山谷捷助力新能源汽车产业高质量发展 L913197600 黄山谷捷制造科技
在新能源汽车产业蓬勃发展的浪潮中，车规级功率半导体作为驱动电机控制系统的核心部件，其性能与稳定性直接关系到汽车的动力输出、能效转化及安全性能。在这一关键领域，黄山谷捷股份有限公司（以下简称“黄山谷捷”或“公司”）以卓越的研发实力、精湛的生产工艺和严格的质量控制体系，成为行业内的佼佼者，特别是在功率半导体散热基板领域，更是树立了新的标杆。自2012年成立以来，黄山谷捷便深谙“科技是第一生产力”的真谛
2020年 12月3日渥太华阴一生守望一人
今天结课了。全面备战，准备期末考试了。最近看到纽约州立阿尔伯尼法学院和西奈山医学院有一个联合生命科学的硕士学位，有点心动，打算考完试以后找教授和相关负责人问一下。新闻方面，中国第一次实现了外太空运载器发射，嫦娥今天正式启程返家了。这也预示着我们面对载人登月又踏出了自己坚实的一步。同时，我们继美国之后在同一年制造出了量子计算机“九章”。“九章”量子计算机可以以200秒的速度计算出当前最强大超级计算机
0416-无题37 傻猪唛的天空之城
办公室外，哗啦啦的下着雨。经过上周闷热，原以为没有春雨了，只是来得晚。天气预报说：本周都是阴雨天气。也好，春天就该是百花盛开，绵绵细雨。刚开始打开编辑器时想发一篇用心写的文章，后来又放弃了。想想有里程碑的意义等过几天再发。日更写得无主题无重点但在末尾我还是用心写了一句鸡汤的啊！给平凡的生活添一点仪式感，自己给自己制造小惊喜。
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
《对生命说是》读书笔记2021-5-27 Diana_58d9
静心技巧——换个视角看待问题。尝试一下这个实验，1坐在椅子上，允许自己全身心的沉浸在你最爱的问题当中，你知道头脑热爱咀嚼他们，记录当你被卷入问题时的感受。2站起来有意识地离开那张椅子，想象你现在离开了你的问题。缓缓的围绕椅子走一圈，从不同的角度看看你的问题。在房间中找一个远离问题的空间，开始仔细深入的看看这个问题，他是真实的还是你制造出来的，同样的状况对于其他人来说会是问题吗？3反复体会作战问题里
开发游戏的学习规划杰克逊的日记游戏学习
第一阶段：●C#语言快速系统地学习一遍（基础的语法、面向对象、基础的数据结构、基础的设计模式）●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验：需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例，将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法，并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
第九章肿瘤放射治疗晨翕
放射物理学：主要研究各种放射源的性能特点、治疗剂量学、质量控制、质量保证及辐射防护等放射生物学：主要研究机体正常组织和肿瘤组织对射线对反应及如何人为地改变这些反应对质和量。放射技术学：主要研究具体运用各种放射源及设备治疗肿瘤患者，包括射野设置、体位固定、定位、摆位操作等技术实施。临床放射肿瘤学：在临床肿瘤学的基础上，研究肿瘤放射治疗的适应证，根据病理、分期、预后确定治疗策略，综合运用放射物理、放射
为了那一个约定王书朋
我和我的学生说好了，不管遇到什么，都要一起努力，这是我们刚遇见时留下的记忆，到现在刚好一年过去。在本周一，我做了一个简单的询问，想看一看经过一个漫长的假期，还有几个人记得努力，所以我一个人一个人的问下去。我所问的内容，就是你有没有记日记和进行课外阅读，两个班将近一百名学生，在我没有要求的情况下。主要是上个学期我们遇到了特殊情况，还没来得及做出要求，就已经进入了假期，因此阴差阳错，为我制造了检验学生
世界十大名牌皮鞋都适合什么性格的人？我信了你滴鞋
前面介绍了《世界公认的五大名鞋，穿过三个以上都是不一般的人》，大概讲了5大名鞋品牌的故事，受到广大读者的关注和讨论，因此在原来的基础上重新整理了世界十大知名皮鞋品牌及特点，揭开他们神秘的面纱，看看到底是哪些人在穿这些鞋子？他们为什么能被公认为是世界排名靠前的品牌？能进入十大名皮鞋的，制造的手工工艺已相近，不同的是品牌设计理念与鞋材选用。正因为每个品牌不同的设计理念，制造出不一样的美丽的产品，适合不
1.8，69 知行思合一
运气动力学万维钢老师提出的名词，不愧是物理博士出身，good1idea，创意一些新名词。开文引用查理芒格的话：得到你想要的东西，最保险的办法，就是让自己配得上你想要的那个东西。接着举例《绝命毒师》Breakingbad导演文斯·吉里根接受采访说的话，引出成功的经验——运气。我们现在所处的这个社会不管是美国还是中国，大体上都是一个精英社会——人们可以靠天赋和努力去争取财富和地位，而不像历史上那样家庭
Day9：别沦为自动化的奴隶——为自己建一座“喷泉广场” 钱塘风华
电子设备解决了小麻烦，却制造了大麻烦。【书名】：混乱——如何成为失控时代的掌控者【作者】：蒂姆哈福德【本书总页码】：288【已读页码】：220（第七章：自动化end）2009年5月31日晚，法航447号航班在电传操作系统失效的情况下，飞行员因习惯了对电传操作系统的依赖，无法对当时的情况作出正确判断，因而也无法作出对应操作——当时的情况：飞机因为急速上升后，过于稀薄的空气密度导致飞机失速，机头抬升，
使用FPGA接收MIPI CSI RX信号并进行去抖动、RGB转YUV处理：FX3014 USB3.0 UVC传输与帧率控制源代码，FPGA实现MIPI CSI RX接收，去Debayer， RGB转 kVfINoSzdrt fpga开发程序人生
fpgamipicsirx接收去debayer,rgb转yuv,fx3014usb3.0uvc传输与帧率控制源代码，具体架构看图，除dphy物理层外，mipi均为源码sensorimx219mipi源码mipi4lanecsirxraw10fpgamachXO3lf-690usb3.0fx301432bityuvdatawithframesync测试模式3280*246415fps1920*108
《京瓷哲学》关于开展日常工作读后感平粤奇妙广东海岛and长隆
至此，又到了《京瓷哲学》这本书的尾声。读书历程，就像在感受一位父母，或者老师，或者是长辈的唠叨和教诲，长篇大论，孜是觉得这些人生的道理谁都会说道两句，当然这种想法很快被印证是错的，没有一颗博爱的心，无私的心，稻盛先生的理念甚至盛和塾可能将不存在。依旧是选择2点分享，第一点制造完美无瑕的产品。随着社会不断的前进发展，人们的标准不再停留于单纯拥有这个层面，而是想拥有更好的。小到日常用餐的摆盘，大到将房
IGBT模块直流参数测试系统STD6500 tianshili029 晶体管参数测试系统半导体特性曲线图示仪
陕西天士立科技有限公司IGBT模块直流参数测试系统STD6500IGBT模块直流参数测试系统ST-DC6500基础信息开发背景：大功率IGBT和Diode模块j静态参数程控式设备技术标准：IEC60747-2/GB/T4023-1997半导体器件分立器件和集成电路第2部分（整流二极管）技术标准：IEC60747-9∶2007/GB/T29332-2012半导体器件分立器件第9部分（绝缘栅双极晶体管
桌面上有多个球在同时运动，怎么实现球之间不交叉，即碰撞？换个号韩国红果果 html 小球碰撞
稍微想了一下，然后解决了很多bug，最后终于把它实现了。其实原理很简单。在每改变一个小球的x y坐标后，遍历整个在dom树中的其他小球，看一下它们与当前小球的距离是否小于球半径的两倍？若小于说明下一次绘制该小球（设为a）前要把他的方向变为原来相反方向（与a要碰撞的小球设为b），即假如当前小球的距离小于球半径的两倍的话，马上改变当前小球方向。那么下一次绘制也是先绘制b，再绘制a，由于a的方向已经改变
《高性能HTML5》读后整理的Web性能优化内容白糖_ html5
读后感先说说《高性能HTML5》这本书的读后感吧，个人觉得这本书前两章跟书的标题完全搭不上关系，或者说只能算是讲解了“高性能”这三个字，HTML5完全不见踪影。个人觉得作者应该首先把HTML5的大菜拿出来讲一讲，再去分析性能优化的内容，这样才会有吸引力。因为只是在线试读，没有机会看后面的内容，所以不胡乱评价了。
[JShop]Spring MVC的RequestContextHolder使用误区 dinguangx jeeshop 商城系统 jshop 电商系统
在spring mvc中，为了随时都能取到当前请求的request对象，可以通过RequestContextHolder的静态方法getRequestAttributes()获取Request相关的变量，如request, response等。在jshop中，对RequestContextHolder的
算法之时间复杂度周凡杨 java 算法时间复杂度效率
在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。这样用大写O()来体现算法时间复杂度的记法，
Java事务处理 g21121 java
一、什么是Java事务通常的观念认为，事务仅与数据库相关。事务必须服从ISO/IEC所制定的ACID原则。ACID是原子性（atomicity）、一致性（consistency）、隔离性（isolation）和持久性（durability）的缩写。事务的原子性表示事务执行过程中的任何失败都将导致事务所做的任何修改失效。一致性表示当事务执行失败时，所有被该事务影响的数据都应该恢复到事务执行前的状
Linux awk命令详解 510888780 linux
一. AWK 说明 awk是一种编程语言，用于在linux/unix下对文本和数据进行处理。数据可以来自标准输入、一个或多个文件，或其它命令的输出。它支持用户自定义函数和动态正则表达式等先进功能，是linux/unix下的一个强大编程工具。它在命令行中使用，但更多是作为脚本来使用。 awk的处理文本和数据的方式：它逐行扫描文件，从第一行到
android permission 布衣凌宇 Permission
<uses-permission android:name="android.permission.ACCESS_CHECKIN_PROPERTIES" ></uses-permission>允许读写访问"properties"表在checkin数据库中，改值可以修改上传 <uses-permission android:na
Oracle和谷歌Java Android官司将推迟 aijuans java oracle
北京时间 10 月 7 日，据国外媒体报道，Oracle 和谷歌之间一场等待已久的官司可能会推迟至 10 月 17 日以后进行，这场官司的内容是 Android 操作系统所谓的 Java 专利权之争。本案法官 William Alsup 称根据专利权专家 Florian Mueller 的预测，谷歌 Oracle 案很可能会被推迟。　　该案中的第二波辩护被安排在 10 月 17 日出庭，从目前看来
linux shell 常用命令 antlove linux shell command
grep [options] [regex] [files] /var/root # grep -n "o" * hello.c:1:/* This C source can be compiled with:
Java解析XML配置数据库连接(DOM技术连接 SAX技术连接) 百合不是茶 sax技术 Java解析xml文档 dom技术 XML配置数据库连接
XML配置数据库文件的连接其实是个很简单的问题,为什么到现在才写出来主要是昨天在网上看了别人写的,然后一直陷入其中,最后发现不能自拔所以今天决定自己完成 ,,,,现将代码与思路贴出来供大家一起学习 XML配置数据库的连接主要技术点的博客; JDBC编程 : JDBC连接数据库 DOM解析XML: DOM解析XML文件 SA
underscore.js 学习（二） bijian1013 JavaScript underscore
Array Functions 所有数组函数对参数对象一样适用。1.first _.first(array, [n]) 别名: head, take 返回array的第一个元素，设置了参数n，就
plSql介绍 bijian1013 oracle 数据库 plsql
/* * PL/SQL 程序设计学习笔记 * 学习plSql介绍.pdf * 时间：2010-10-05 */ --创建DEPT表 create table DEPT ( DEPTNO NUMBER(10), DNAME NVARCHAR2(255), LOC NVARCHAR2(255) ) delete dept; select
【Nginx一】Nginx安装与总体介绍 bit1129 nginx
启动、停止、重新加载Nginx nginx 启动Nginx服务器，不需要任何参数u nginx -s stop 快速(强制)关系Nginx服务器 nginx -s quit 优雅的关闭Nginx服务器 nginx -s reload 重新加载Nginx服务器的配置文件 nginx -s reopen 重新打开Nginx日志文件
spring mvc开发中浏览器兼容的奇怪问题 bitray jquery Ajax springMVC 浏览器上传文件
最近个人开发一个小的OA项目,属于复习阶段.使用的技术主要是spring mvc作为前端框架,mybatis作为数据库持久化技术.前台使用jquery和一些jquery的插件. 在开发到中间阶段时候发现自己好像忽略了一个小问题,整个项目一直在firefox下测试,没有在IE下测试,不确定是否会出现兼容问题.由于jquer
Lua的io库函数列表 ronin47 lua io
1、io表调用方式：使用io表，io.open将返回指定文件的描述，并且所有的操作将围绕这个文件描述　　io表同样提供三种预定义的文件描述io.stdin,io.stdout,io.stderr 　　2、文件句柄直接调用方式,即使用file:XXX()函数方式进行操作,其中file为io.open()返回的文件句柄　　多数I/O函数调用失败时返回nil加错误信息,有些函数成功时返回nil
java-26-左旋转字符串 bylijinnan java
public class LeftRotateString { /** * Q 26 左旋转字符串 * 题目：定义字符串的左旋转操作：把字符串前面的若干个字符移动到字符串的尾部。 * 如把字符串abcdef左旋转2位得到字符串cdefab。 * 请实现字符串左旋转的函数。要求时间对长度为n的字符串操作的复杂度为O(n)，辅助内存为O(1)。 */ pu
《vi中的替换艺术》-linux命令五分钟系列之十一 cfyme linux命令
vi方面的内容不知道分类到哪里好，就放到《Linux命令五分钟系列》里吧！今天编程，关于栈的一个小例子，其间我需要把”S.”替换为”S->”(替换不包括双引号)。其实这个不难，不过我觉得应该总结一下vi里的替换技术了，以备以后查阅。 1 所有替换方案都要在冒号“:”状态下书写。 2 如果想将abc替换为xyz，那么就这样 :s/abc/xyz/ 不过要特别
[轨道与计算]新的并行计算架构 comsci 并行计算
我在进行流程引擎循环反馈试验的过程中，发现一个有趣的事情。。。如果我们在流程图的每个节点中嵌入一个双向循环代码段，而整个流程中又充满着很多并行路由，每个并行路由中又包含着一些并行节点，那么当整个流程图开始循环反馈过程的时候，这个流程图的运行过程是否变成一个并行计算的架构呢？
重复执行某段代码 dai_lm android
用handler就可以了 private Handler handler = new Handler(); private Runnable runnable = new Runnable() { public void run() { update(); handler.postDelayed(this, 5000); } }; 开始计时 h
Java实现堆栈（list实现） datageek 数据结构——堆栈
public interface IStack<T> { //元素出栈，并返回出栈元素 public T pop(); //元素入栈 public void push(T element); //获取栈顶元素 public T peek(); //判断栈是否为空 public boolean isEmpty
四大备份MySql数据库方法及可能遇到的问题 dcj3sjt126com DB backup
一：通过备份王等软件进行备份前台进不去？用备份王等软件进行备份是大多老站长的选择，这种方法方便快捷，只要上传备份软件到空间一步步操作就可以，但是许多刚接触备份王软件的客用户来说还原后会出现一个问题：因为新老空间数据库用户名和密码不统一，网站文件打包过来后因没有修改连接文件，还原数据库是好了，可是前台会提示数据库连接错误，网站从而出现打不开的情况。解决方法：学会修改网站配置文件，大多是由co
github做webhooks：[1]钩子触发是否成功测试 dcj3sjt126com github git webhook
转自: http://jingyan.baidu.com/article/5d6edee228c88899ebdeec47.html github和svn一样有钩子的功能，而且更加强大。例如我做的是最常见的push操作触发的钩子操作，则每次更新之后的钩子操作记录都会在github的控制板可以看到！工具/原料 github 方法/步骤
">的作用" target="_blank">JSP中的作用蕃薯耀
JSP中<base href="<%=basePath%>">的作用 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
linux下SAMBA服务安装与配置 hanqunfeng linux
局域网使用的文件共享服务。一.安装包： rpm -qa | grep samba samba-3.6.9-151.el6.x86_64 samba-common-3.6.9-151.el6.x86_64 samba-winbind-3.6.9-151.el6.x86_64 samba-client-3.6.9-151.el6.x86_64 samba-winbind-clients
guava cache IXHONG cache
缓存，在我们日常开发中是必不可少的一种解决性能问题的方法。简单的说，cache 就是为了提升系统性能而开辟的一块内存空间。　　缓存的主要作用是暂时在内存中保存业务系统的数据处理结果，并且等待下次访问使用。在日常开发的很多场合，由于受限于硬盘IO的性能或者我们自身业务系统的数据处理和获取可能非常费时，当我们发现我们的系统这个数据请求量很大的时候，频繁的IO和频繁的逻辑处理会导致硬盘和CPU资源的
Query的开始--全局变量,noconflict和兼容各种js的初始化方法 kvhur JavaScript jquery css
这个是整个jQuery代码的开始，里面包含了对不同环境的js进行的处理，例如普通环境，Nodejs，和requiredJs的处理方法。还有jQuery生成$, jQuery全局变量的代码和noConflict代码详解完整资源： http://www.gbtags.com/gb/share/5640.htm jQuery 源码： (
美国人的福利和中国人的储蓄 nannan408
今天看了篇文章，震动很大，说的是美国的福利。美国医院的无偿入院真的是个好措施。小小的改善，对于社会是大大的信心。小孩，税费等，政府不收反补，真的体现了人文主义。美国这么高的社会保障会不会使人变懒？答案是否定的。正因为政府解决了后顾之忧，人们才得以倾尽精力去做一些有创造力，更造福社会的事情，这竟成了美国社会思想、人
N阶行列式计算(JAVA) qiuwanchi N阶行列式计算
package gaodai; import java.util.List; /** * N阶行列式计算 * @author 邱万迟 * */ public class DeterminantCalculation { public DeterminantCalculation(List<List<Double>> determina
C语言算法之打渔晒网问题 qiufeihu c 算法
如果一个渔夫从2011年1月1日开始每三天打一次渔，两天晒一次网，编程实现当输入2011年1月1日以后任意一天，输出该渔夫是在打渔还是在晒网。代码如下： #include <stdio.h> int leap(int a) /*自定义函数leap()用来指定输入的年份是否为闰年*/ { if((a%4 == 0 && a%100 != 0
XML中DOCTYPE字段的解析 wyzuomumu xml
DTD声明始终以!DOCTYPE开头,空一格后跟着文档根元素的名称,如果是内部DTD,则再空一格出现[],在中括号中是文档类型定义的内容. 而对于外部DTD,则又分为私有DTD与公共DTD,私有DTD使用SYSTEM表示,接着是外部DTD的URL. 而公共DTD则使用PUBLIC,接着是DTD公共名称,接着是DTD的URL. 私有DTD <!DOCTYPErootSYST

半导体器件物理 2022.10.13

你可能感兴趣的:(半导体器件物理-复旦大学,制造)