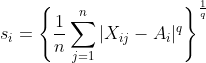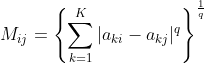聚类算法常用内部评价指标——轮廓系数、Calinski-Harabasz Index(CH)、Davies-Bouldin Index(DB)
聚类分析的评价指标也称为:性能度量指标
聚类算法聚类后,如何评价聚类结果,如何确定各聚类算法结果的优劣,如何确定聚类算法的参数值,可以通过聚类性能度量指标从一个侧面说明聚类算法和算法参数的选择。、
聚类性能度量指标分为外部指标和内部指标。
外部指标,也就是有参考标准的指标,通常也可以称为有监督情况下的一种度量聚类算法和各参数的指标。具体就是聚类算法的聚类结果和已知的(有标签的、人工标准或基于一种理想的聚类的结果)相比较,从而衡量设计的聚类算法的性能、优劣。
内部指标是无监督的,无需基准数据集,不需要借助于外部参考模型,利用样本数据集中样本点与聚类中心之间的距离来衡量聚类结果的优劣
内部指标主要有:
1)紧密度(Compactness):每个聚类簇中的样本点到聚类中心的平均距离。对应聚类结果,需要使用所有簇的紧密度的平均值来衡量聚类算法和聚类各参数选取的优劣。紧密度越小,表示簇内的样本点越集中,样本点之间聚类越短,也就是说簇内相似度越高。
2)分割度(Seperation):是个簇的簇心之间的平均距离。分割度值越大说明簇间间隔越远,分类效果越好,即簇间相似度越低。
3)误差平方和 (SSE:Sum of squares of errors):类中数据聚类距离类中心的平方损失之和,即K-means算法的优化目标,表示为
其中,![]() 表示第k个类中第i个样本点,
表示第k个类中第i个样本点,![]() 表示第k个类的中心点。
表示第k个类的中心点。
核心代码段
def distance_sum_max_min_avg(self, class_list, dis_matrix):
sum = 0
max = 0
min = math.inf
for index in range(len(class_list)):
value = dis_matrix[class_list[index]][index]
sum += value
if max < value:
max = value
if min > value:
min = value
avg = sum/len(class_list)
return sum,max,min,avg4)轮廓系数 (Silhouette Coefficient):对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1],同类别样本距离越相近,不同类别样本距离越远,分数越高。
针对某个样本的轮廓系数s为:
其中,a表示某个样本与其所在簇内其他样本的平均距离,b表示某个样本与其他簇样本的平均距离。
聚类总的轮廓系数SC为:
核心代码段
def silhou ette_coefficient(self,data_num, cluster, dis_matrix):
sum = 0
for index in range(data_num):
cluster_in = 0
cluster_in_num = 0
cluster_out = 0
cluster_out_num = 0
for class_index in range(len(cluster)):
if index == class_index:
continue
elif cluster[index] == cluster[class_index]:
cluster_in_num += 1
cluster_in += dis_matrix[index][class_index]
else:
cluster_out_num += 1
cluster_out += dis_matrix[index][class_index]
sum += (cluster_out / cluster_out_num - cluster_in / cluster_in_num) / max(cluster_out / cluster_out_num,
cluster_in / cluster_in_num)
sc = sum / data_num
return sc轮廓系数为-1时表示聚类结果不好,为+1时表示簇内实例之间紧凑,为0时表示有簇重叠。轮廓系数越大,表示簇内实例之间紧凑,簇间距离大,这正是聚类的标准概念。
对于簇结构为凸的数据轮廓系数值高,而对于簇结构非凸需要使用DBSCAN进行聚类的数据,轮廓系数值低,因此,轮廓系数不应该用来评估不同聚类算法之间的优劣,比如Kmeans聚类结果与DBSCAN聚类结果之间的比较。
5)Calinski-Harabasz Index(CH): Calinski-Harabasz指数的本质是簇间距离与簇内距离的比值,且整体计算过程与方差计算方式类似,所以又将其称之为方差比准则。
将容量为 N 的数据集合 X 聚成 K 类,通过计算类内各点与类中心的距离平方和来度量类内的紧密度(类内距离),各个类中心点与数据集中心点距离平方和来度量数据集的分离度(类间距离)。
CH指标的计算公式为:
其中 ![]() 为类间的协方差矩阵,
为类间的协方差矩阵, ![]() 类内数据的协方差矩阵,详细公式如下:
类内数据的协方差矩阵,详细公式如下:
其中![]() 表示类q的中心点,
表示类q的中心点,![]() 表示数据集的中心点,
表示数据集的中心点,![]() 表示类q中的数据的数目,
表示类q中的数据的数目,![]() 表示类q的数据集合。
表示类q的数据集合。
Calinski-Harabasz指数的分数越大说明越好(类别内部协方差越小越好,类别之间协方差越大越好)
核心代码段
import pandas as pd
import numpy as np
from sklearn import metrics
from sklearn.cluster import KMeans
dataframe = pd.DataFrame(data=np.random.randint(0, 60, size=(100, 10)))
# 以kmeans聚类方法为例
kmeans_model = KMeans(n_clusters=5, random_state=1).fit(dataframe)
labels = kmeans_model.labels_
score = metrics.calinski_harabasz_score(dataframe, labels)
print(score)
5)Davies-Bouldin Index(DB):由大卫L·戴维斯和唐纳德·Bouldin提出)是一种评估是一种评估度量的聚类算法。
DB计算任意两类别的类内距离平均之和除以该两类中心距离,并求最大值。DB越小意味着类内距离越小同时类间距离越大。
其中![]() 表示类中样本点分散度,
表示类中样本点分散度,![]() 则就是第i类与第j类中心的距离。计算公式如下所示:
则就是第i类与第j类中心的距离。计算公式如下所示:
其中![]() 表示第i类中第j个数据点;
表示第i类中第j个数据点;![]() 表示第i类的中心;n表示第i类中数据点的个数;q取1表示:各点到中心的距离的均值,q取2时表示:各点到中心距离的标准差,它们都可以用来衡量分散程度。
表示第i类的中心;n表示第i类中数据点的个数;q取1表示:各点到中心的距离的均值,q取2时表示:各点到中心距离的标准差,它们都可以用来衡量分散程度。
其中![]() 表示第i类的中心点的第K个属性的值。
表示第i类的中心点的第K个属性的值。
核心代码段
def davies_bouldin(self,center_student_dis_matrix,center_center_dis_matrix,class_list):
# 对于每个簇计算分散度
cluster_num = len(center_student_dis_matrix)
S = [0] * cluster_num
for index in range(cluster_num):
sum = 0
n = 0
for class_index in range(len(class_list)):
if index == class_list[class_index]:
n += 1
sum += center_student_dis_matrix[index][class_index]
S[index] = sum/n
Ri = []
for i in range(len(S)):
Rij = []
for j in range(len(S)):
if i != j:
r_temp = (S[i] + S[j])/center_center_dis_matrix[i][j]
Rij.append(r_temp)
Ri.append(max(Rij))
return np.mean(Ri)分类个数的不同可以导致不同的值,DB值越小,分类效果越好。
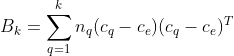
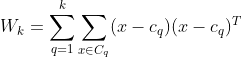
![DB =\frac{1 }{k}\sum^k_{i=1}\mathop{max}\limits_{i\ne j,i,j\in[1,K]}\frac{s_i+s_j }{M_i_j}](http://img.e-com-net.com/image/info8/e24240ac61234356b48d377745b288db.gif)