【菜菜的sklearn课堂笔记】支持向量机-硬间隔与软间隔：重要参数C

视频作者：菜菜TsaiTsai
链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili

我们之前在理论推导中使用的数据都有一个特点，那就是他们或是完全线性可分，或者是非线性的数据。在我们对比核函数时，实际上用到了一种不同的数据，那就是不完全线性可分的数据集。比如说如下数据集：

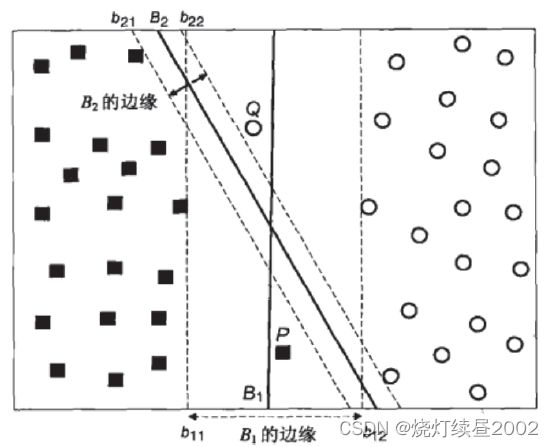
这个数据集和我们最开始介绍SVM如何工作的时候的数据集一模一样，除了多了P和Q两个点。
我们注意到，虽然决策边界$B_1$的间隔已经非常宽了，然而点P和Q依然被分错了类别，相反，边际比较小的$B_2$却正确地分出了点P和Q的类别。这里并不是说$B_2$此时此刻就是一条更好的边界了，与之前的论述中一致，如果我们引入更多的训练数据，或引入测试数据，$B_1$更加宽敞的边界可以帮助它又更好的表现。但是，和之前不一样，现在即便是让边际最大的决策边界$B_1$的训练误差也不可能为0了。此时，我们就需要引入“软间隔”的概念：
关键概念：硬间隔与软间隔：当两组数据是完全线性可分，我们可以找出一个决策边界使得训练集上的分类误差为0，这两种数据就被称为是存在”硬间隔“的。当两组数据几乎是完全线性可分的，但决策边界在训练集上存在较小的训练误差，这两种数据就被称为是存在”软间隔“。
我们可以通过调整我们对决策边界的定义，将硬间隔时得出的数学结论推广到软间隔的情况上，让决策边界能够忍受一小部分训练误差。这个时候，我们的决策边界就不是单纯地寻求最大边际了，因为对于软间隔地数据来说，边际越大被分错的样本也就会越多，因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。

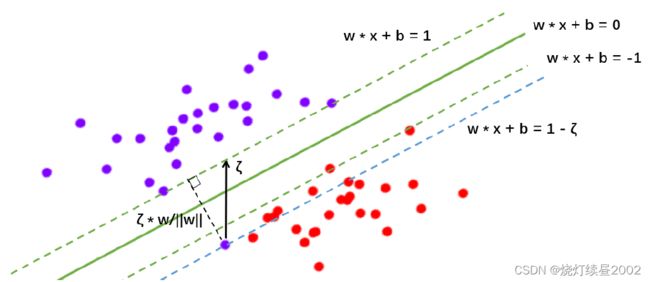
看上图，原始的决策边界$\omega \cdot x+b=0$，原本的平行于决策边界的两个虚线超平面$\omega \cdot x+b=1$和$\omega \cdot x+b=-1$都依然有效，我们原始的判别函数为
$$\{\begin{array}{rl}& \omega \cdot x_i+b\ge 1if{y}_i=1\\ & \omega \cdot x_i+b\le -1if{y}_i=-1\end{array}$$
不过，这些超平面现在无法让数据上的训练误差等于0了，因为此时存在了一个混杂在红色点中的紫色点$x_p$。于是，我们需要放松我们原始判别函数中的不等条件，来让决策边界能够适用于我们的异常点，于是我们引入松弛系数$\zeta$来帮助我们优化原始的判别函数：
$$\{\begin{array}{rl}& \omega \cdot x_i+b\ge 1-{\zeta }_{i}if{y}_i=1\\ & \omega \cdot x_i+b\le -1+{\zeta }_{i}if{y}_i=-1\end{array}$$
其中${\zeta }_i>0$
可以看得出，这其实是将原本的虚线超平面向图像的上方和下方平移，其符号的处理方式和我们原本讲解过的把符号放入$\omega$是一模一样的方式。

这里我们使$\zeta >0$就是超平面上移，$\zeta <0$就是超平面下移

松弛系数其实很好理解，来看上面的图像。位于红色点附近的紫色点$x_p$在原本的判别函数中必定会被分为红色，所以一定会被判断错。现在我们作一条与决策边界平行，但是过点$x_p$的直线$\omega \cdot x_i=1-{\zeta }_i$（图中的蓝色虚线）。这条直线是由$\omega \cdot x_i+b=1$平移得到，所以两条直线在纵坐标上的差异就是$\zeta$（竖直的黑色箭头）。而点$x_p$到$\omega \cdot x_i+b=1$的距离就可以表示为$\begin{array}{r}\frac{\zeta \cdot \omega }{||\omega ||}\end{array}$，即$\zeta$在$\omega$方向上的投影。由于单位向量是固定的，所以$\zeta$可以作为点$x_p$在原始的决策边界上的分类错误的程度的表示，隔得越远，分得越错。但注意， $\zeta$并不是点到决策超平面的距离本身。

在软间隔的条件下，我们仍然是有支持向量的，只是此时$\omega \cdot x_i+b\ne \pm 1$

不难注意到，如果我们让$\omega \cdot x_i+b\ge 1-{\zeta }_i$作为我们的新决策超平面，是有一定的问题的，虽然我们把异常的紫色点分类正确了，但我们同时也分错了一系列红色的点。所以我们必须在我们求解最大边际的损失函数中加上一个惩罚项，用来惩罚我们具有巨大松弛系数的决策超平面。现在，我们的损失函数为：
$$\{\begin{array}{rl}& \underset{\omega ,b,\zeta }{\min }\frac{||\omega |{|}^2}{2}+C\sum _{i=1}^N{\zeta }_i\\ & y_i(\omega \cdot \Phi (x_i)+b)\ge 1-{\zeta }_i,i=1,2,\cdots ,N\\ & {\zeta }_i\ge 0,i=1,2,\cdots ,N\end{array}$$
其中C是用来控制惩罚项的惩罚力度的系数。
拉格朗日函数也被松弛系数改变
$$L(\omega ,b,\alpha ,\zeta )=\frac{1}{2}||\omega |{|}^2+C\sum _{i=1}^N{\zeta }_i-\sum _{i=1}^N{\alpha }_i(y_i(\omega \cdot \Phi (x_i)+b)-1+{\zeta }_i)-\sum _{i=1}^N{\mu }_i{\zeta }_i$$
需要满足的KKT条件为
$$\begin{array}{r}\{\begin{array}{rl}& \frac{\partial L}{\partial \omega }=\frac{\partial L}{\partial b}=\frac{\partial L}{\partial \delta }=0\\ & {\zeta }_i\ge 0,{\alpha }_i\ge 0,{\mu }_i\ge 0\\ & {\alpha }_i(y_i(\omega \cdot \Phi (x_i)+b)-1+{\zeta }_i)=0\\ & {\mu }_i{\zeta }_i=0\end{array}\end{array}$$
拉格朗日对偶函数也被松弛系数改变
$$\{\begin{array}{rl}& L_D=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\Phi (x_i)\Phi (x_j)\\ & C\ge {\alpha }_i\ge 0\end{array}$$
这种状况下的拉格朗日对偶函数看起来和线性可分状况下的对偶函数一模一样，但是需要注意的是，在这个函数中，拉格朗日乘数$\alpha$的取值的限制改变了。在硬间隔的状况下，拉格朗日乘数值需要大于等于0，而现在它被要求不能够大于用来控制惩罚项的惩罚力度的系数C。有了对偶函数之后，我们的求解过程和硬间隔下的步骤一致。
以上所有的公式，是以线性硬间隔数据为基础，考虑了软间隔存在的情况和数据是非线性的状况而得来的。而这些公式，就是sklearn类SVC背后使用的最终公式。公式中现在唯一的新变量，松弛系数的惩罚力度C，由我们的参数C来进行控制。

重要参数C

参数C用于权衡”训练样本的正确分类“与”决策函数的边际最大化“两个不可同时完成的目标，希望找出一个平衡点来让模型的效果最佳。
参数C：浮点数，默认1，必须大于等于0，可不填。松弛系数的惩罚项系数。如果C值设定比较大，那SVC可能会选择边际较小的，能够更好地分类所有训练点的决策边界，不过模型的训练时间也会更长。如果C的设定值较小，那SVC会尽量最大化边界，决策功能会更简单，但代价是训练的准确度。

我们不能说满足$\omega \cdot x_i+b\ge 1-{\zeta }_i$，就有$y_i=1$，因为此时是软间隔，可能出现两个虚线超平面分割出共用的空间
就像是上图的情况，$\omega \cdot x_i+b=1-{\zeta }_i$和$\omega \cdot x_i+b=-1$，如果我们选择这两条作为决策边界，就会有很多红色的点可能被分类错误，训练集上的误差就会很大，也就对应着我们C很小的情况
多说一句，个人理解，因为C很小的时候，即$\begin{array}{r}\underset{\omega ,b,\zeta }{\min }\frac{||\omega |{|}^2}{2}+C\sum _{i=1}^N{\zeta }_i\end{array}$的后一项$\begin{array}{r}C\sum _{i=1}^N{\zeta }_i\end{array}$中的C很小，那么较大的$\zeta$也不会对整个决策函数有很大的影响，因此超平面允许上下移动的范围会很大

在实际使用中，C和核函数的相关参数（gamma，degree等等）们搭配，往往是SVM调参的重点。与gamma不同，C没有在对偶函数中出现，并且是明确了调参目标的，所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1，通常来说这都是一个合理的参数。** 如果我们的数据很嘈杂，那我们往往减小C**。
我们也可以使用网格搜索或者学习曲线来调整C的值。这里我们尝试学习曲线的方式

score = []
C_range = np.linspace(0.01,30,50) # C不能为负数
for i in C_range:
    clf = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
    
print(max(score),C_range[score.index(max(score))])
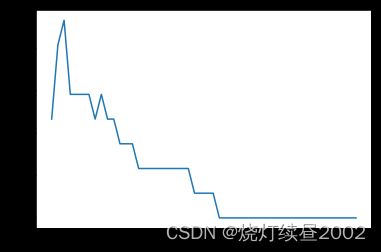
plt.plot(C_range,score)
plt.show()
---
0.9766081871345029 1.2340816326530613

进一步减小区间

score = []
C_range = np.linspace(0.01,5,50)
for i in C_range:
    clf = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
    
print(max(score),C_range[score.index(max(score))])
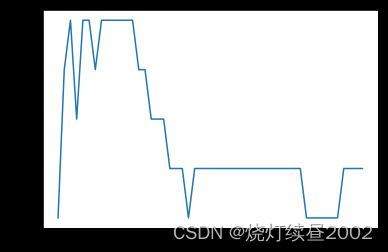
plt.plot(C_range,score)
plt.show()
---
0.9766081871345029 0.2136734693877551

对于rbf同理

score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
    clf = SVC(kernel="rbf",C=i
              ,gamma=0.012067926406393264
              ,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
    
print(max(score),C_range[score.index(max(score))])
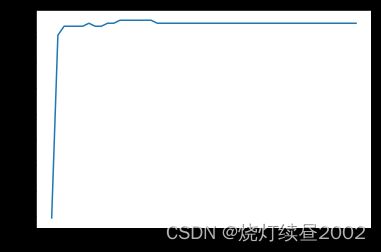
plt.plot(C_range,score)
plt.show()
---
0.9824561403508771 6.7424489795918365

细化

score = []
C_range = np.linspace(5,7,50) # C不能为负数
for i in C_range:
    clf = SVC(kernel="rbf",C=i
              ,gamma=0.012067926406393264
              ,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
    
print(max(score),C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
---
0.9824561403508771 6.224489795918367

此时，我们找到了乳腺癌数据集上的最优解：rbf核函数下的98.24%的准确率。当然，我们还可以使用交叉验证来改进我们的模型，获得不同测试集和训练集上的交叉验证结果。

其实我们只是找到了在一个测试集和训练集上的最好表现的C，因此交叉验证是十分必要的

软间隔的支持向量

软间隔条件下（指定C的条件下），所有可能影响我们的超平面的样本可能都会被定义为支持向量，所以支持向量就不再是所有压在虚线超平面上的点，而是所有可能影响我们的超平面的位置的那些混杂在彼此的类别中的点了（也就是被错误分类的点）。

这个代码类似地之前写过，在支持向量的边界颜色有改而已

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_circles,make_moons,make_blobs,make_classification
from sklearn.svm import SVC

n_samples = 100
datasets = [
    make_moons(n_samples=n_samples,noise=0.2,random_state=0)
    ,make_circles(n_samples=n_samples,noise=0.2,factor=0.5,random_state=1)
    ,make_blobs(n_samples=n_samples,centers=2,random_state=5)
    ,make_classification(n_samples=n_samples,n_features=2,n_informative=2,n_redundant=0,random_state=5)
]

Kernel = ["linear"]
nrows = len(datasets)
ncols = len(Kernel) + 1

fig, axes = plt.subplots(nrows,ncols,figsize=(10,16))
for ds_cnt, (X, Y) in enumerate(datasets):

    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    ax.scatter(X[:,0],X[:,1],c=Y
               ,zorder=10,cmap=plt.cm.Paired,edgecolors="k"
              )
    ax.set_xticks([])
    ax.set_yticks([])
    
    for est_idx, kernel in enumerate(Kernel):
        ax = axes[ds_cnt, est_idx + 1]
        
        clf = SVC(kernel=kernel, gamma=2, C=1).fit(X,Y)
        # 不断增大C，决策边界可能会旋转，虚线超平面会向决策边界靠拢
        score = clf.score(X,Y)
        
        ax.scatter(X[:,0],X[:,1],c=Y
                   ,zorder=10,cmap=plt.cm.Paired,edgecolors="k"
                  )
        
        ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100
                  ,facecolors="none",zorder=10,edgecolors='white')
        
        x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
        y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
        
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
        
        ax.pcolormesh(XX,YY,Z > 0, cmap=plt.cm.Paired)
        
        ax.contour(XX,YY,Z,colors=['k','k','k'],linestyles=['--','-','--']
                   ,levels=[-1,0,1])
        ax.set_xticks([])
        ax.set_yticks([])
        
        if ds_cnt == 0:
            ax.set_title(kernel)
        
        ax.text(0.95, 0.06
               ,('%.2f' %score).lstrip('0')
               ,size=15
               ,bbox=dict(boxstyle='round',alpha=0.8,facecolor='white')
               ,transform=ax.transAxes
               ,horizontalalignment='right')
        
plt.tight_layout()
plt.show()
# 这些被白色框圈出的点当做支持向量，也就是说虚线超平面都可能过这些向量
# 只是现在选出了在指定参数的情况下对应决策函数最好的一个

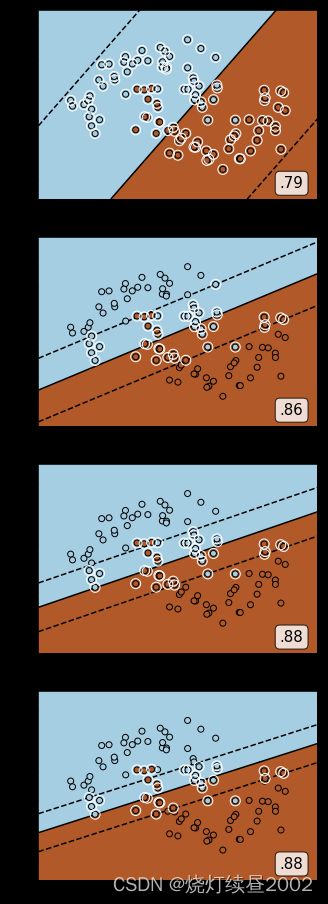
白色圈圈出的就是我们的支持向量，可以看到，所有在两条虚线超平面之间的点，和虚线超平面外，但属于另一个类别的点，都被我们认为是支持向量。并不是因为这些点都在我们的超平面上，而是因为我们的超平面由所有的这些点来决定，我们可以通过调节C来移动我们的超平面，让超平面过任何一个白色圈圈出的点。参数C就是这样影响了我们的决策，可以说是彻底改变了支持向量机的决策过程。

随着C的增大，虚线超平面会逐渐向决策边界靠近，并且有时决策边界还会旋转

X,y = make_moons(n_samples=n_samples,noise=0.2,random_state=0)
fig, axes = plt.subplots(4,1,figsize=(5,16))
for i,n in zip(range(4),[0.01,0.5,1,10]):
    clf = SVC(kernel="linear",C=n,gamma=2).fit(X,y)
    score = clf.score(X,y)
    ax = axes[i]
    # 指定subplots只有一列时，axes索引也只需要一个元素
    ax.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.Paired,zorder=10,edgecolors='k')
    ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100
                ,facecolors="none" # 点的颜色是透明
                # 这里不能直接使用前面的y，因为support_vectors_的数量和y的数量是不一样的
                ,zorder=10,edgecolors='white')
    # 如果不写zorder=10会被后面画的图覆盖
    x_min,x_max = X[:,0].min() - .5,X[:,0].max() + .5
    y_min,y_max = X[:,1].min() - .5,X[:,1].max() + .5
    XX,yy = np.mgrid[x_min:x_max:200j,y_min:y_max:200j]
    Z = clf.decision_function(np.c_[XX.ravel(), yy.ravel()]).reshape(XX.shape)
    ax.pcolormesh(XX,yy,Z > 0, cmap=plt.cm.Paired)
    ax.contour(XX,yy,Z,levels=[-1,0,1],linestyles=['--','-','--'],colors=['k','k','k'])
    ax.text(0.95, 0.06
               ,('%.2f' %score).lstrip('0')
               ,size=15
               ,bbox=dict(boxstyle='round',alpha=0.8,facecolor='white')
               ,transform=ax.transAxes
               ,horizontalalignment='right')

plt.show() # 注意plt.show()的位置，第一次show()后面的图显示不出来