Bishop 模式识别与机器学习读书笔记_ch3.3 广义线性回归模型
ch3.3 广义线性回归模型
回归问题的目标是在给定 D D D 维输入(input)变量 x \boldsymbol{x} x 的情况下,预测⼀个或者多个连续目标(target)变量 t t t 的值。线性回归模型(如多项式回归)是输入变量的线性函数,有着可调节的参数,具有线性函数的性质。但是,通过将⼀组输入变量的非线性函数进行线性组合,我们可以获得⼀类更加有用的函数,被称为基函数(basis function)。
**注释:**这样的模型是参数的线性函数,这使得其具有⼀些简单的分析性质,同时关于输入变量是非线性的。
回归问题: 给定⼀个由 N N N 个观测值 { x n } \{\boldsymbol{x}_n\} {xn} 组成的数据集,其中 n = 1 , ⋯ , N n = 1,\cdots, N n=1,⋯,N,以及对应的目标值 { t n } \{t_n\} {tn},我们的目标是预测对于给定新的值的情况 x \boldsymbol{x} x 下 t t t 的值。最简单的方法是,直接建立⼀个适当的函数 y ( x ) y(\boldsymbol{x}) y(x),对于新的输入 x \boldsymbol{x} x,这个函数能够直接给出对应的 t t t 的预测。更⼀般地,从⼀个概率的观点来看,我们的目标是对预测分布 p ( t ∣ x ) p(t\vert\boldsymbol{x}) p(t∣x) 建模,因为它表达了对于 x \boldsymbol{x} x 而言的 t t t 不确定性。从这个条件概率分布中,对于任意的 x \boldsymbol{x} x 的新值,我们可以对 t t t 进行预测,这种方法等同于最小化⼀个恰当选择的损失函数的期望值。
**注释:**虽然线性模型对于模式识别的实际应用来说有很大的局限性,特别是对于涉及到高维输入空间的问题来说更是如此,但是他们有很好的分析性质,并且为讨论更加复杂的模型提供了基础。
1. 线性基函数模型
**线性回归模型:**对于 D D D 维数据 x = ( x 1 , x 2 , ⋯ , x D ) \boldsymbol{x}=(x_1,x_2,\cdots,x_D) x=(x1,x2,⋯,xD) , 回归问题的最简单模型是输入变量的线性组合
y ( x , w ) = w 0 + w 1 x 1 + ⋯ + w D x D = w T x = x T w y(\boldsymbol{x},\boldsymbol{w})=w_0+w_1x_1+\cdots+w_Dx_D=\boldsymbol{w}^T\boldsymbol{x}=\boldsymbol{x}^T\boldsymbol{w} y(x,w)=w0+w1x1+⋯+wDxD=wTx=xTw
该模型是关于参数 w 1 , w 2 , ⋯ , w D w_1,w_2,\cdots,w_D w1,w2,⋯,wD 的线性模型,同时也是变量 x i x_i xi 的线性函数。
**问题:**线性模型的结构(关于变量 x i x_i xi 的线性函数)使得模型在应用过程中具有明显的不足,特别是解决非线性问题。
策略:引入变量 x \boldsymbol{x} x 的非线性函数 ϕ j ( x ) \phi_j(\boldsymbol{x}) ϕj(x) ,称为基函数。
推广后的模型为
y ( x , w ) = w T ϕ ( x ) = w 0 + w 1 ϕ 1 ( x ) + ⋯ + w M − 1 ϕ M − 1 ( x ) = w 0 + ∑ j = 1 M − 1 ϕ j ( x ) \begin{align} y(\boldsymbol{x},\boldsymbol{w})&=\boldsymbol{w}^T\boldsymbol{\phi}(\boldsymbol{x}) \\ &=w_0+w_1\phi_1(\boldsymbol{x})+\cdots+w_{M-1}\phi_{M-1}(\boldsymbol{x}) \\ &=w_0+\sum_{j=1}^{M-1}\phi_j(\boldsymbol{x}) \end{align} y(x,w)=wTϕ(x)=w0+w1ϕ1(x)+⋯+wM−1ϕM−1(x)=w0+j=1∑M−1ϕj(x)
其中, M M M 为模型参数的个数, w = ( w 0 , w 1 , ⋯ , w M − 1 ) T \boldsymbol{w}=(w_0,w_1,\cdots,w_{M-1})^T w=(w0,w1,⋯,wM−1)T, ϕ = ( ϕ 0 , ϕ 1 , ⋯ , ϕ M − 1 ) T \boldsymbol{\phi}=(\phi_0,\phi_1,\cdots,\phi_{M-1})^T ϕ=(ϕ0,ϕ1,⋯,ϕM−1)T, ϕ 0 = 1 \phi_0=1 ϕ0=1。
注释:
- 基函数 ϕ j \phi_j ϕj 是对一个样本的所有特征进行的非线性变换,而非对样本的某一个特征做的非线性变换,且变换的类型非常多,形成了基向量 ϕ \boldsymbol{\phi} ϕ.
- 应用非线性基函数后,模型变为输入变量 x \boldsymbol{x} x 的非线性函数,但对于参数 w \boldsymbol{w} w 而言,仍然是线性模型。
几个常见的基函数:
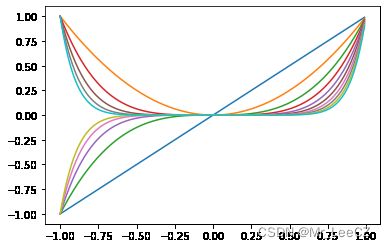
(1) 多项式基函数
ϕ j ( x ) = x j \phi_j(x)=x^j ϕj(x)=xj
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-1,1,0.01)
p = [1,2,3,4,5,6,7,8,9,10]
for t in p:
y = np.power(x,t)
plt.plot(x,y)
plt.show()
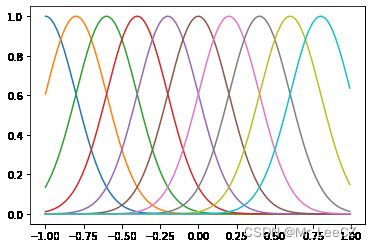
(2) 径向基函数(“高斯”基函数)
ϕ j ( x ) = exp { − ( x − μ j ) 2 2 s 2 } \phi_j(x)=\exp\Bigg\{-\frac{(x-\mu_j)^2}{2s^2}\Bigg\} ϕj(x)=exp{−2s2(x−μj)2}
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
s = 0.2
x = np.arange(-1,1,0.01)
Mu = np.arange(-1,1,0.2)
for mu in Mu:
y = np.exp(-np.power(x-mu,2)/2/s/s)
plt.plot(x,y)
plt.show()
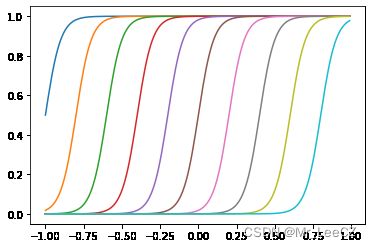
(3) sigmoid 基函数
ϕ j ( x ) = σ ( x − μ s ) \phi_j(x)=\sigma(\frac{x-\mu}{s}) ϕj(x)=σ(sx−μ)
其中,
σ ( a ) = 1 1 + exp ( − a ) \sigma(a)=\frac{1}{1+\exp(-a)} σ(a)=1+exp(−a)1
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def sig(a):
return 1/(1+np.exp(-a))
s = 0.05
x = np.arange(-1,1,0.01)
Mu = np.arange(-1,1,0.2)
for mu in Mu:
y = sig((x-mu)/s)
plt.plot(x,y)
plt.show()
2. 极大似然与最小二乘法
假设目标 t t t 由确定函数 y ( x , w ) y(\boldsymbol{x},\boldsymbol{w}) y(x,w) 和高斯噪声的和生成
t = y ( x , w ) + ϵ t=y(\boldsymbol{x},\boldsymbol{w})+\epsilon t=y(x,w)+ϵ
其中, ϵ ∼ N ( 0 , β − 1 ) \epsilon\sim \mathcal{N}(0,\beta^{-1}) ϵ∼N(0,β−1),因此,可以记作
p ( t ∣ x , w , β ) = N ( t ∣ y ( x , w ) , β − 1 ) p(t\vert\boldsymbol{x},\boldsymbol{w},\beta)=\mathcal{N}\Big(t\vert y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1}\Big) p(t∣x,w,β)=N(t∣y(x,w),β−1)
对于输入 X = { x 1 , x 2 , ⋯ , x N } \boldsymbol{X}=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_N\} X={x1,x2,⋯,xN},目标向量 t = { t 1 , t 2 , ⋯ , t N } \boldsymbol{t}=\{t_1,t_2,\cdots,t_N\} t={t1,t2,⋯,tN}, 似然函数可表示为
p ( t ∣ X , w , β ) = ∏ n = 1 N N ( t n ∣ ϕ ( x n ) T w , β − 1 ) = ∏ n = 1 N 1 Z exp { − 1 2 β ⋅ ( t n − ϕ ( x n ) T w ) 2 } \begin{align} p(\boldsymbol{t}\vert\boldsymbol{X},\boldsymbol{w},\beta)&=\prod_{n=1}^N\mathcal{N}\Big(t_n\vert\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w},\beta^{-1}\Big) \\ &=\prod_{n=1}^N\frac{1}{Z}\exp\Big\{-\frac{1}{2}\beta\cdot\Big(t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big)^2\Big\} \end{align} p(t∣X,w,β)=n=1∏NN(tn∣ϕ(xn)Tw,β−1)=n=1∏NZ1exp{−21β⋅(tn−ϕ(xn)Tw)2}
log 似然可以表示为
ln p ( t ∣ X , w , β ) = ln ∏ n = 1 N 1 Z exp { − 1 2 β ⋅ ( t n − ϕ ( x n ) T w ) 2 } = − ln Z − 1 2 β ∑ n = 1 N { t n − ϕ ( x n ) T w } 2 \begin{align} \ln p(\boldsymbol{t}\vert\boldsymbol{X},\boldsymbol{w},\beta) &=\ln\prod_{n=1}^N\frac{1}{Z}\exp\Big\{-\frac{1}{2}\beta\cdot\Big(t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big)^2\Big\}\\ &=-\ln Z-\frac{1}{2}\beta\sum_{n=1}^N\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}^2 \end{align} lnp(t∣X,w,β)=lnn=1∏NZ1exp{−21β⋅(tn−ϕ(xn)Tw)2}=−lnZ−21βn=1∑N{tn−ϕ(xn)Tw}2
log 似然函数关于 w \boldsymbol{w} w 的导数表示为
∇ ln p ( t ∣ X , w , β ) = − β ∑ n = 1 N { − ϕ ( x n ) } ⋅ { t n − ϕ ( x n ) T w } = β ∑ n = 1 N ϕ ( x n ) ⋅ { t n − ϕ ( x n ) T w } = β { ∑ n = 1 N t n ϕ ( x n ) − ∑ n = 1 N ϕ ( x n ) ⋅ ϕ ( x n ) T w } = β { ∑ n = 1 N t n ϕ ( x n ) − ∑ n = 1 N ϕ ( x n ) ⋅ ϕ ( x n ) T w } = β { t 1 ϕ ( x 1 ) + t 2 ϕ ( x 2 ) + ⋯ + t N ϕ ( x N ) } − β { ϕ ( x 1 ) ⋅ ϕ ( x 1 ) T + ϕ ( x 2 ) ⋅ ϕ ( x 2 ) T + ⋯ + ϕ ( x N ) ⋅ ϕ ( x N ) T } w = β ( ϕ ( x 1 ) , ϕ ( x 2 ) , ⋯ , ϕ ( x N ) ) ( t 1 t 2 ⋮ t N ) − β ( ϕ ( x 1 ) , ϕ ( x 2 ) , ⋯ , ϕ ( x N ) ) ( ϕ ( x 1 ) T ϕ ( x 2 ) T ⋮ ϕ ( x N ) T ) w = β ( ϕ 0 ( x 1 ) ϕ 0 ( x 2 ) ⋯ ϕ 0 ( x N ) ϕ 1 ( x 1 ) ϕ 1 ( x 2 ) ⋯ ϕ 1 ( x N ) ⋮ ⋮ ⋮ ϕ M − 1 ( x 1 ) ϕ M − 1 ( x 2 ) ⋯ ϕ M − 1 ( x N ) ) ⏟ Φ ( t 1 t 2 ⋮ t N ) − β ( ϕ 0 ( x 1 ) ϕ 0 ( x 2 ) ⋯ ϕ 0 ( x N ) ϕ 1 ( x 1 ) ϕ 1 ( x 2 ) ⋯ ϕ 1 ( x N ) ⋮ ⋮ ⋮ ϕ M − 1 ( x 1 ) ϕ M − 1 ( x 2 ) ⋯ ϕ M − 1 ( x N ) ) ⏟ Φ ( ϕ ( x 1 ) T ϕ ( x 2 ) T ⋮ ϕ ( x N ) T ) ⏟ Φ T w = β Φ t − β Φ Φ T w \begin{align} \nabla \ln p(\boldsymbol{t}\vert\boldsymbol{X},\boldsymbol{w},\beta) &=-\beta\sum_{n=1}^N\Big\{-\boldsymbol{\phi}(\boldsymbol{x}_n)\Big\}\cdot\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}\\ &=\beta\sum_{n=1}^N\boldsymbol{\phi}(\boldsymbol{x}_n)\cdot\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}\\ &=\beta\Big\{\sum_{n=1}^Nt_n\boldsymbol{\phi}(\boldsymbol{x}_n)-\sum_{n=1}^N\boldsymbol{\phi}(\boldsymbol{x}_n)\cdot\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}\\ &=\beta\Big\{\sum_{n=1}^Nt_n\boldsymbol{\phi}(\boldsymbol{x}_n)-\sum_{n=1}^N\boldsymbol{\phi}(\boldsymbol{x}_n)\cdot\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}\\ &=\beta\Big\{t_1\boldsymbol{\phi}(\boldsymbol{x}_1)+t_2\boldsymbol{\phi}(\boldsymbol{x}_2)+\cdots+t_N\boldsymbol{\phi}(\boldsymbol{x}_N)\Big\}\\ &\;\;\;-\beta\Big\{\boldsymbol{\phi}(\boldsymbol{x}_1)\cdot\boldsymbol{\phi}(\boldsymbol{x}_1)^T+\boldsymbol{\phi}(\boldsymbol{x}_2)\cdot\boldsymbol{\phi}(\boldsymbol{x}_2)^T+\cdots+\boldsymbol{\phi}(\boldsymbol{x}_N)\cdot\boldsymbol{\phi}(\boldsymbol{x}_N)^T\Big\}\boldsymbol{w}\ &=\beta\Bigg(\boldsymbol{\phi}(\boldsymbol{x}_1),\boldsymbol{\phi}(\boldsymbol{x}_2),\cdots,\boldsymbol{\phi}(\boldsymbol{x}_N)\Bigg)\left( \begin{array}{c} %该矩阵一共3列,每一列都居中放置 t_1\\ %第一行元素 t_2\\ %第二行元素 \vdots \\ t_N \end{array} \right) \\ &\;\;\;-\beta\Bigg(\boldsymbol{\phi}(\boldsymbol{x}_1),\boldsymbol{\phi}(\boldsymbol{x}_2),\cdots,\boldsymbol{\phi}(\boldsymbol{x}_N)\Bigg)\left( \begin{array}{c} %该矩阵一共3列,每一列都居中放置 \boldsymbol{\phi}(\boldsymbol{x}_1)^T\\ %第一行元素 \boldsymbol{\phi}(\boldsymbol{x}_2)^T\\ %第二行元素 \vdots \\ \boldsymbol{\phi}(\boldsymbol{x}_N)^T \end{array} \right) \boldsymbol{w}\\ &=\beta\underbrace{\left( \begin{array}{cccc} %该矩阵一共3列,每一列都居中放置 \phi_0(\boldsymbol{x}_1)&\phi_0(\boldsymbol{x}_2)&\cdots&\phi_0(\boldsymbol{x}_N)\\ %第一行元素 \phi_1(\boldsymbol{x}_1)&\phi_1(\boldsymbol{x}_2)&\cdots&\phi_1(\boldsymbol{x}_N)\\ %第二行元素 \vdots&\vdots& &\vdots \\ \phi_{M-1}(\boldsymbol{x}_{1})&\phi_{M-1}(\boldsymbol{x}_2)&\cdots&\phi_{M-1}(\boldsymbol{x}_N)\\ %第二行元素 \end{array} \right)}_{\boldsymbol{\Phi}}\left( \begin{array}{c} %该矩阵一共3列,每一列都居中放置 t_1\\ %第一行元素 t_2\\ %第二行元素 \vdots \\ t_N \end{array} \right) \\ &\;\;\;-\beta\underbrace{\left( \begin{array}{cccc} %该矩阵一共3列,每一列都居中放置 \phi_0(\boldsymbol{x}_1)&\phi_0(\boldsymbol{x}_2)&\cdots&\phi_0(\boldsymbol{x}_N)\\ %第一行元素 \phi_1(\boldsymbol{x}_1)&\phi_1(\boldsymbol{x}_2)&\cdots&\phi_1(\boldsymbol{x}_N)\\ %第二行元素 \vdots&\vdots& &\vdots \\ \phi_{M-1}(\boldsymbol{x}_{1})&\phi_{M-1}(\boldsymbol{x}_2)&\cdots&\phi_{M-1}(\boldsymbol{x}_N)\\ %第二行元素 \end{array} \right)}_{\boldsymbol{\Phi}}\underbrace{\left( \begin{array}{c} %该矩阵一共3列,每一列都居中放置 \boldsymbol{\phi}(\boldsymbol{x}_1)^T\\ %第一行元素 \boldsymbol{\phi}(\boldsymbol{x}_2)^T\\ %第二行元素 \vdots \\ \boldsymbol{\phi}(\boldsymbol{x}_N)^T \end{array} \right)}_{\boldsymbol{\Phi}^T} \boldsymbol{w}\\ &=\beta\boldsymbol{\Phi}\boldsymbol{t}-\beta\boldsymbol{\Phi}\boldsymbol{\Phi}^T\boldsymbol{w}\tag{1} \end{align} ∇lnp(t∣X,w,β)=−βn=1∑N{−ϕ(xn)}⋅{tn−ϕ(xn)Tw}=βn=1∑Nϕ(xn)⋅{tn−ϕ(xn)Tw}=β{n=1∑Ntnϕ(xn)−n=1∑Nϕ(xn)⋅ϕ(xn)Tw}=β{n=1∑Ntnϕ(xn)−n=1∑Nϕ(xn)⋅ϕ(xn)Tw}=β{t1ϕ(x1)+t2ϕ(x2)+⋯+tNϕ(xN)}−β{ϕ(x1)⋅ϕ(x1)T+ϕ(x2)⋅ϕ(x2)T+⋯+ϕ(xN)⋅ϕ(xN)T}w −β(ϕ(x1),ϕ(x2),⋯,ϕ(xN))⎝ ⎛ϕ(x1)Tϕ(x2)T⋮ϕ(xN)T⎠ ⎞w=βΦ ⎝ ⎛ϕ0(x1)ϕ1(x1)⋮ϕM−1(x1)ϕ0(x2)ϕ1(x2)⋮ϕM−1(x2)⋯⋯⋯ϕ0(xN)ϕ1(xN)⋮ϕM−1(xN)⎠ ⎞⎝ ⎛t1t2⋮tN⎠ ⎞−βΦ ⎝ ⎛ϕ0(x1)ϕ1(x1)⋮ϕM−1(x1)ϕ0(x2)ϕ1(x2)⋮ϕM−1(x2)⋯⋯⋯ϕ0(xN)ϕ1(xN)⋮ϕM−1(xN)⎠ ⎞ΦT ⎝ ⎛ϕ(x1)Tϕ(x2)T⋮ϕ(xN)T⎠ ⎞w=βΦt−βΦΦTw=β(ϕ(x1),ϕ(x2),⋯,ϕ(xN))⎝ ⎛t1t2⋮tN⎠ ⎞(1)
令 log 似然的梯度 (1) 为 0 \boldsymbol{0} 0 得,
w = ( Φ Φ T ) − 1 Φ t \boldsymbol{w}=(\boldsymbol{\Phi}\boldsymbol{\Phi}^T)^{-1}\boldsymbol{\Phi}\boldsymbol{t} w=(ΦΦT)−1Φt
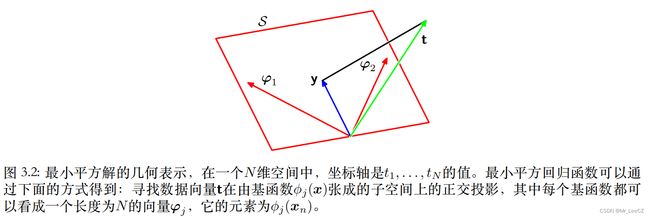
极大似然的几何解释:
3. 正则化最小二乘法
为了控制过拟合现象,可引入正则化技术,将独立于数据的误差融入总误差函数,并通过一个正则化系数 λ \lambda λ 进行折中,得
E D ( w ) + λ E W ( w ) (2) E_D(\boldsymbol{w})+\lambda E_W(\boldsymbol{w})\tag{2} ED(w)+λEW(w)(2)
通常基于数据的误差函数为
E D ( w ) = 1 2 ∑ n = 1 N { t n − ϕ ( x n ) T w } 2 E_D(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^N\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}^2 ED(w)=21n=1∑N{tn−ϕ(xn)Tw}2
一种简单的正则项可建模为权向量的平方和
E W ( w ) = 1 2 w T w E_W(\boldsymbol{w})=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w} EW(w)=21wTw
则公式(1)可变形为
J = 1 2 ∑ n = 1 N { t n − ϕ ( x n ) T w } 2 + λ 2 w T w = 1 2 ( t 1 − ϕ ( x 1 ) T w , t 2 − ϕ ( x 2 ) T w , ⋯ , t n − ϕ ( x n ) T w ) ( t 1 − ϕ ( x 1 ) T w t 2 − ϕ ( x 2 ) T w ⋮ t N − ϕ ( x N ) T w ) + λ 2 w T w = 1 2 ( t − Φ T w ) T ( t − Φ T w ) + λ 2 w T w \begin{align} J&=\frac{1}{2}\sum_{n=1}^N\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}^2+\frac{\lambda}{2}\boldsymbol{w}^T\boldsymbol{w}\\ &=\frac{1}{2}\Big(t_1-\boldsymbol{\phi}(\boldsymbol{x}_1)^T\boldsymbol{w},t_2-\boldsymbol{\phi}(\boldsymbol{x}_2)^T\boldsymbol{w},\cdots,t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big)\left( \begin{array}{c} %该矩阵一共3列,每一列都居中放置 t_1-\boldsymbol{\phi}(\boldsymbol{x}_1)^T\boldsymbol{w}\\ %第一行元素 t_2-\boldsymbol{\phi}(\boldsymbol{x}_2)^T\boldsymbol{w}\\ %第二行元素 \vdots \\ t_N-\boldsymbol{\phi}(\boldsymbol{x}_N)^T\boldsymbol{w} \end{array} \right)+\frac{\lambda}{2}\boldsymbol{w}^T\boldsymbol{w}\\ &=\frac{1}{2}\Big(\boldsymbol{t}-\boldsymbol{\Phi}^T\boldsymbol{w}\Big)^T\Big(\boldsymbol{t}-\boldsymbol{\Phi}^T\boldsymbol{w}\Big)+\frac{\lambda}{2}\boldsymbol{w}^T\boldsymbol{w} \end{align} J=21n=1∑N{tn−ϕ(xn)Tw}2+2λwTw=21(t1−ϕ(x1)Tw,t2−ϕ(x2)Tw,⋯,tn−ϕ(xn)Tw)⎝ ⎛t1−ϕ(x1)Twt2−ϕ(x2)Tw⋮tN−ϕ(xN)Tw⎠ ⎞+2λwTw=21(t−ΦTw)T(t−ΦTw)+2λwTw
则
∂ J ∂ w = − Φ ( t − Φ T w ) + λ w = ( λ I + Φ Φ T ) w − Φ t = 0 \frac{\partial J}{\partial \boldsymbol{w}}=-\boldsymbol{\Phi}\Big(\boldsymbol{t}-\boldsymbol{\Phi}^T\boldsymbol{w}\Big)+\lambda\boldsymbol{w}=\Big(\lambda\boldsymbol{I}+\boldsymbol{\Phi}\boldsymbol{\Phi}^T\Big)\boldsymbol{w}-\boldsymbol{\Phi}\boldsymbol{t}=\boldsymbol{0} ∂w∂J=−Φ(t−ΦTw)+λw=(λI+ΦΦT)w−Φt=0
得
w = ( λ I + Φ T ) − 1 Φ t \boldsymbol{w}=\Big(\lambda\boldsymbol{I}+\boldsymbol{\Phi}^T\Big)^{-1}\boldsymbol{\Phi}\boldsymbol{t} w=(λI+ΦT)−1Φt
更一般的正则化框架误差函数为
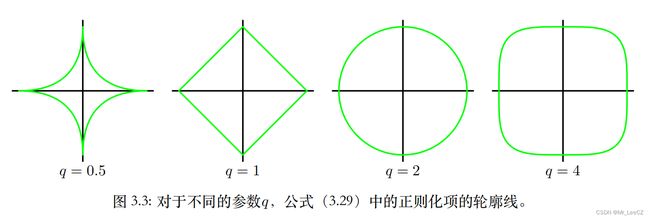
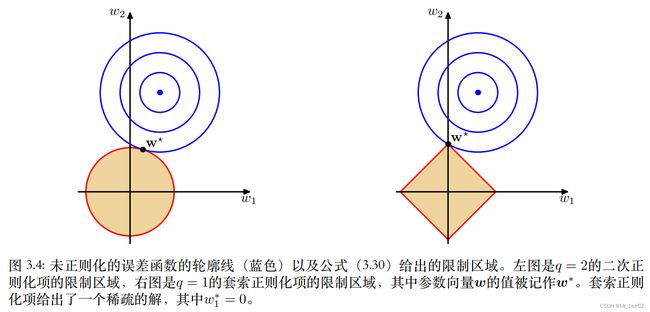
J 1 = 1 2 ∑ n = 1 N { t n − ϕ ( x n ) T w } 2 + λ 2 ∑ j = 1 M ∣ w ∣ q J_1=\frac{1}{2}\sum_{n=1}^N\Big\{t_n-\boldsymbol{\phi}(\boldsymbol{x}_n)^T\boldsymbol{w}\Big\}^2+\frac{\lambda}{2}\sum_{j=1}^M\vert w\vert^q J1=21n=1∑N{tn−ϕ(xn)Tw}2+2λj=1∑M∣w∣q
当 q = 1 q=1 q=1 时,模型称为 lasso 模型, λ \lambda λ 充分大时,参数的分量逐渐变为 0 0 0,从而获得稀疏解。
当 q q q 取不同的值时,正则项对应不同的形状,如下图所示,
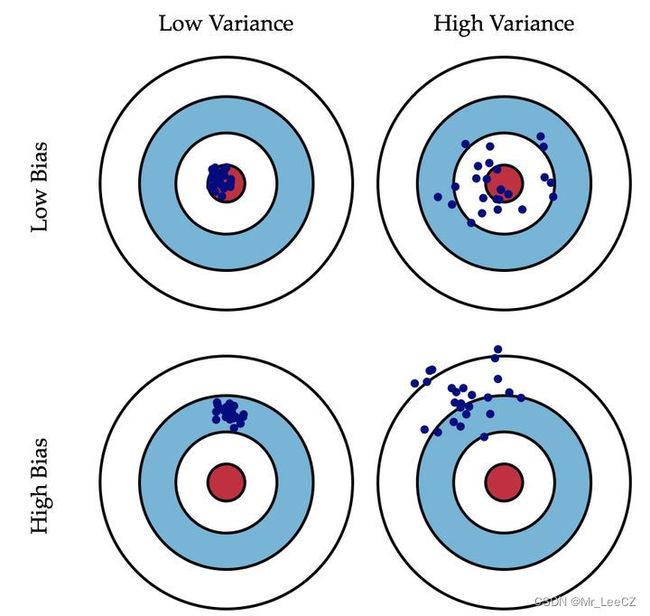
4. 偏置-方差分解
因变量的条件期望(观测数据的集中趋势,数据本身决定的,与模型无关)
h ( x ) = E [ t ∣ x ] = ∫ t p ( x ) d x h(\boldsymbol{x})=\mathbb{E}[t\vert \boldsymbol{x}]=\int tp(\boldsymbol{x})d\boldsymbol{x} h(x)=E[t∣x]=∫tp(x)dx
因变量的条件方差(观测数据的分散程度)
v a r [ t ∣ x ] = ∫ { t − E [ t ∣ x ] } 2 p ( t ∣ x ) d x = ∫ { t − h ( x ) } 2 p ( t ∣ x ) d x var[t\vert \boldsymbol{x}]=\int\big\{t-\mathbb{E}[t\vert \boldsymbol{x}]\big\}^2p(t\vert\boldsymbol{x})d\boldsymbol{x}=\int\big\{t-h(\boldsymbol{x})\big\}^2p(t\vert\boldsymbol{x})d\boldsymbol{x} var[t∣x]=∫{t−E[t∣x]}2p(t∣x)dx=∫{t−h(x)}2p(t∣x)dx
此项与最优拟合曲线 y ( x ) y(\boldsymbol{x}) y(x) 无关,表示观测数据的扰动,称为噪声项。
E [ L ] = ∫ { y ( x ) − h ( x ) } 2 p ( x ) d x + ∬ { h ( x ) − t } 2 p ( x , t ) d x d t ⏟ ∫ v a r [ t ∣ x ] p ( x ) d x \mathbb{E}[L]=\int\{y(\boldsymbol{x})-h(\boldsymbol{x})\}^2p(\boldsymbol{x})d\boldsymbol{x}+\underbrace{\iint\{h(\boldsymbol{x})-t\}^2p(\boldsymbol{x},t)d\boldsymbol{x}dt}_{\int var[t\vert \boldsymbol{x}]p(\boldsymbol{x})d\boldsymbol{x}} E[L]=∫{y(x)−h(x)}2p(x)dx+∫var[t∣x]p(x)dx ∬{h(x)−t}2p(x,t)dxdt
由于最优拟合曲线 y ( x ) y(\boldsymbol{x}) y(x) 是观测数据的估计,与观测数据有直接关系,因此可记作 y ( x ; D ) y(\boldsymbol{x};\mathcal{D}) y(x;D);又因为估计结果有可能多解或者抽样多次形成不同的样本,因此,拟合曲线的平均趋势表示为 y ‾ ( x , D ) = E D [ y ( x ; D ) ] \overline{y}(\boldsymbol{x},\mathcal{D})=\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})] y(x,D)=ED[y(x;D)],称为平均拟合曲线。
{ y ( x ; D ) − h ( x ) } 2 = { { y ( x ; D ) − E D [ y ( x ; D ) ] } + { E D [ y ( x ; D ) ] − h ( x ) } } 2 = { y ( x ; D ) − E D [ y ( x ; D ) ] } 2 + { E D [ y ( x ; D ) ] − h ( x ) } 2 2 { y ( x ; D ) − E D [ y ( x ; D ) ] } ⏟ 期望为 0 { E D [ y ( x ; D ) ] − h ( x ) } \begin{align} \{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x})\}^2&=\Bigg\{\Big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\Big\}+\Big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\Big\}\Bigg\}^2 \\ &=\Big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\Big\}^2+\Big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\Big\}^2 \\ &\;\;\;\;\;\;\;2\underbrace{\Big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\Big\}}_{期望为 0}\Big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\Big\} \\ \end{align} {y(x;D)−h(x)}2={{y(x;D)−ED[y(x;D)]}+{ED[y(x;D)]−h(x)}}2={y(x;D)−ED[y(x;D)]}2+{ED[y(x;D)]−h(x)}22期望为0 {y(x;D)−ED[y(x;D)]}{ED[y(x;D)]−h(x)}
E D [ { y ( x ; D ) − h ( x ) } 2 ] = E D [ { y ( x ; D ) − E D [ y ( x ; D ) ] } 2 ] + E D [ { E D [ y ( x ; D ) ] − h ( x ) } 2 ⏟ 与观测数据集无关 ] = E D [ { y ( x ; D ) − E D [ y ( x ; D ) ] } 2 ] ⏟ 所有拟合曲线的方差 + { E D [ y ( x ; D ) ] − h ( x ) } 2 ⏟ 平均曲线与最优曲线的偏差平方 \begin{align}\mathbb{E}_{\mathcal{D}}\Big[\{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x})\}^2\Big]&=\mathbb{E}_{\mathcal{D}}\Big[\big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\big\}^2\Big]+\mathbb{E}_{\mathcal{D}}\Big[\underbrace{\big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\big\}^2}_{与观测数据集无关}\Big] \\ &=\underbrace{\mathbb{E}_{\mathcal{D}}\Big[\big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\big\}^2\Big]}_{所有拟合曲线的方差}+\underbrace{\big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\big\}^2}_{平均曲线与最优曲线的偏差平方} \\ \end{align} ED[{y(x;D)−h(x)}2]=ED[{y(x;D)−ED[y(x;D)]}2]+ED[与观测数据集无关 {ED[y(x;D)]−h(x)}2]=所有拟合曲线的方差 ED[{y(x;D)−ED[y(x;D)]}2]+平均曲线与最优曲线的偏差平方 {ED[y(x;D)]−h(x)}2
综上
E [ L ] = ∫ { E D [ y ( x ; D ) ] − h ( x ) } 2 p ( x ) d x ⏟ 偏差的平方: ( b i a s ) 2 + ∫ E D [ { y ( x ; D ) − E D [ y ( x ; D ) ] } 2 ] p ( x ) d x ⏟ 方差 v a r i a n c e + ∬ { h ( x ) − t } 2 p ( x , t ) d x d t ⏟ 与曲线拟合无关的噪声项: ∫ v a r [ t ∣ x ] p ( x ) d x \begin{align} \mathbb{E}[L]&=\underbrace{\int\big\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\big\}^2p(\boldsymbol{x})d\boldsymbol{x}}_{偏差的平方:(bias)^2} \\ &+\underbrace{\int\mathbb{E}_{\mathcal{D}}\Big[\big\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\big\}^2\Big]p(\boldsymbol{x})d\boldsymbol{x}}_{方差 variance} \\ &+\underbrace{\iint\{h(\boldsymbol{x})-t\}^2p(\boldsymbol{x},t)d\boldsymbol{x}dt}_{与曲线拟合无关的噪声项:\int var[t\vert \boldsymbol{x}]p(\boldsymbol{x})d\boldsymbol{x}} \end{align} E[L]=偏差的平方:(bias)2 ∫{ED[y(x;D)]−h(x)}2p(x)dx+方差variance ∫ED[{y(x;D)−ED[y(x;D)]}2]p(x)dx+与曲线拟合无关的噪声项:∫var[t∣x]p(x)dx ∬{h(x)−t}2p(x,t)dxdt
即
expected loss = ( bias ) 2 + variance + noise \text{expected loss}\;=(\text{bias})^2+\text{variance}+\text{noise} expected loss=(bias)2+variance+noise
**注释:**偏差-方差分解是频率学派的观点,依赖于来自于总体的样本数据及样本量,但是我们并不知道总体,这就不能很好地解决过拟合问题,需要通过其它理论解决。