sklearn基础篇(五)-- 线性模型
1 用于回归的线性模型
线性回归的目的是要得到输出向量 Y \pmb{Y} YYY和输入特征 X \pmb{X} XXX之间的线性关系,求出线性回归系数 θ \pmb{\theta} θθθ,也就是 Y = X θ \pmb{Y}=\pmb{X\theta} YYY=XθXθXθ。其中 Y \pmb{Y} YYY的维度为 m × 1 m \times 1 m×1, X \pmb{X} XXX的维度为 m × n m\times n m×n,而 θ \pmb{\theta} θθθ的维度为 n × 1 n \times 1 n×1。 m m m代表样本个数, n n n代表样本特征的维度。
提示:为了书写方便,这里的 θ \pmb{\theta} θθθ是把权重和偏置合在一个矩阵里,输入特征也增加一维,全部为1。
1.1 普通最小二乘法
线性回归,或者普通最小二乘法(ordinary least squares,OLS),是回归问题最简单也最经典的线性方法。均方误差(mean squared error)是预测值与真实值之差的平方和除以样本数。线性回归没有参数,这是一个优点,但也因此无法控制模型的复杂度。 LinearRegression类就是我们平时说的最常见普通的线性回归,它的损失函数也是最简单的,如下:
J ( θ ) = 1 2 ( X θ − Y ) T ( X θ − Y ) J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) J(θ)=21(Xθ−Y)T(Xθ−Y)
scikit中的LinearRegression类用的是最小二乘法。通过最小二乘法,可以解出线性回归系数 θ \pmb{\theta} θθθ为:
θ = ( X T X ) − 1 X T Y \mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y} θ=(XTX)−1XTY
之前的文章已经讲过这部分的公式推导,请阅读:高数篇(三)-- 最小二乘法、正则化
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)
“斜率”参数( w \pmb{w} www,也叫作权重或系数)被保存在coef_属性中,而偏移或截距( b b b)被保存在intercept_属性中:
print("lr.coef: {}".format(lr.coef_)) # lr.coef: [0.39390555]
print("lr.intercept_: {}".format(lr.intercept_)) # lr.intercept_: -0.031804343026759746
intercept_属性是一个浮点数,而coef_属性是一个NumPy 数组,每个元素对应一个输入特征。由于wave 数据集中只有一个输入特征,所以lr.coef_ 中只有一个元素。
我们来看一下训练集和测试集的性能:
print("Training set score: {:.2f}".format(lr.score(X_train, y_train))) # Training set score: 0.67
print("Test set score: {:.2f}".format(lr.score(X_test, y_test))) # Test set score: 0.66
R 2 R^2 R2约为0.66,这个结果不是很好,但我们可以看到,训练集和测试集上的分数非常接近。这说明可能存在欠拟合,而不是过拟合。对于这个一维数据集来说,过拟合的风险很小,因为模型非常简单(或受限)。然而,对于更高维的数据集(即有大量特征的数据集),线性模型将变得更加强大,过拟合的可能性也会变大。我们来看一下LinearRegression在更复杂的数据集上的表现,比如波士顿房价数据集。像前面一样构建线性回归模型:
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
比较一下训练集和测试集的分数就可以发现,我们在训练集上的预测非常准确,但测试集上的 R 2 R^2 R2要低很多:
print("Training set score: {:.2f}".format(lr.score(X_train, y_train))) # Training set score: 0.95
print("Test set score: {:.2f}".format(lr.score(X_test, y_test))) # Test set score: 0.61
训练集和测试集之间的性能差异是过拟合的明显标志,因此我们应该试图找到一个可以控制复杂度的模型。标准线性回归最常用的替代方法之一就是岭回归(ridge regression),下面来看一下。
1.2 岭回归
由于上一节的LinearRegression没有考虑过拟合的问题,有可能泛化能力较差,这时损失函数可以加入正则化项,如果加入的是L2范数的正则化项,这就是Ridge回归。损失函数如下:
J ( θ ) = 1 2 ( X θ − Y ) T ( X θ − Y ) + 1 2 α ∣ ∣ θ ∣ ∣ 2 2 J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \frac{1}{2}\alpha||\theta||_2^2 J(θ)=21(Xθ−Y)T(Xθ−Y)+21α∣∣θ∣∣22
其中 α \alpha α为常数系数,需要进行调优。 ∣ ∣ θ ∣ ∣ 2 ||θ||_2 ∣∣θ∣∣2为L2范数。
Ridge回归在不抛弃任何一个特征的情况下,缩小了回归系数,使得模型相对而言比较的稳定,不至于过拟合。
通过最小二乘法,可以解出线性回归系数 θ \theta θ为:
θ = ( X T X + α E ) − 1 X T Y \mathbf{\theta = (X^TX + \alpha E)^{-1}X^TY} θ=(XTX+αE)−1XTY
其中 E \pmb{E} EEE为单位矩阵。
对扩展的波士顿房价数据集的效果如何:
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train))) # Training set score: 0.89
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test))) # Test set score: 0.75
可以看出,Ridge在训练集上的分数要低于LinearRegression,但在测试集上的分数更高。这和我们的预期一致。线性回归对数据存在过拟合。Ridge 是一种约束更强的模型,所以更不容易过拟合。 复杂度更小的模型意味着在训练集上的性能更差,但泛化性能更好。
Ridge 模型在模型的简单性(系数都接近于0)与训练集性能之间做出权衡。简单性和训练集性能二者对于模型的重要程度可以由用户通过设置alpha 参数来指定。在前面的例子中,我们用的是默认参数alpha=1.0。但没有理由认为这会给出最佳权衡。alpha 的最佳设定值取决于用到的具体数据集。增大alpha 会使得系数更加趋向于0,从而降低训练集性能,但可能会提高泛化性能。例如:
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train))) # Training set score: 0.79
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test))) # Test set score: 0.64
减小alpha 可以让系数受到的限制更小,对于非常小的alpha 值,系数几乎没有受到限制,我们得到一个与LinearRegression类似的模型:
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train))) # Training set score: 0.93
print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test))) # Test set score: 0.77
这里alpha=0.1 似乎效果不错。我们可以尝试进一步减小alpha 以提高泛化性能。
更大的alpha表示约束更强的模型,所以我们预计大alpha对应的coef_元素比小alpha对应的coef_元素要小。这一点可以在下图中得到证实:
import matplotlib.pyplot as plt
plt.plot(ridge.coef_, 's', label="Ridge alpha=1")
plt.plot(ridge10.coef_, '^', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0, 0, len(lr.coef_)) # 画水平线
plt.ylim(-25, 25)
plt.legend()
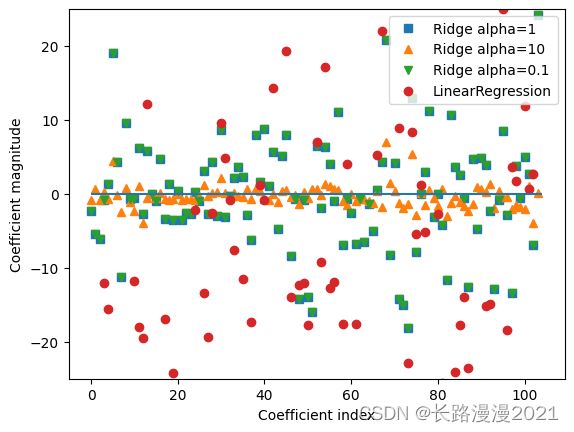
x 轴对应coef_的元素,即第几个特征,对于alpha=10,系数大多在-3 和3 之间。对于alpha=1 的Ridge 模型,系数要稍大一点。对于alpha=0.1,点的范围更大。对于没有做正则化的线性回归(即alpha=0),点的范围很大,许多点都超出了图像的范围。
对波士顿房价数据集做二次抽样,并在数据量逐渐增加的子数据集上分别对LinearRegression和Ridge(alpha=1)两个模型进行评估(将模型性能作为数据集大小的函数进行绘图,这样的图像叫作学习曲线):
mglearn.plots.plot_ridge_n_samples()

正如所预计的那样,无论是岭回归还是线性回归,所有数据集大小对应的训练分数都要高于测试分数。由于岭回归是正则化的,因此它的训练分数要整体低于线性回归的训练分数。但岭回归的测试分数要更高,特别是对较小的子数据集。如果少于400 个数据点,线性回归学不到任何内容。随着模型可用的数据越来越多,两个模型的性能都在提升,最终线性回归的性能追上了岭回归。这里要记住的是,如果有足够多的训练数据,正则化变得不那么重要,并且岭回归和线性回归将具有相同的性能。
1.3 Lasso正则化
线性回归的 L 1 L_1 L1正则化通常称为Lasso回归,它和Ridge回归的区别是在损失函数上增加了的是 L 1 L_1 L1正则化的项,而不是 L 2 L_2 L2正则化项。 L 1 L_1 L1正则化的项也有一个常数系数 α \alpha α来调节损失函数的均方差项和正则化项的权重,具体Lasso回归的损失函数表达式如下:
J ( θ ) = 1 2 m ( X θ − Y ) T ( X θ − Y ) + α ∣ ∣ θ ∣ ∣ 1 J(\mathbf\theta) = \frac{1}{2m}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1 J(θ)=2m1(Xθ−Y)T(Xθ−Y)+α∣∣θ∣∣1
其中 n n n为样本个数, α \alpha α为常数系数,需要进行调优。 ∣ ∣ θ ∣ ∣ 1 ||\theta||_1 ∣∣θ∣∣1为L1范数。Lasso回归可以使得一些特征的系数变小,甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。
Lasso回归的损失函数优化方法常用的有两种,坐标轴下降法和最小角回归法。Lasso类采用的是坐标轴下降法,LassoLars类采用的是最小角回归法。
将lasso 应用在扩展的波士顿房价数据集上:
from sklearn.linear_model import Lasso
import numpy as np
lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ != 0)))
Training set score: 0.29
Test set score: 0.21
Number of features used: 4
可以发现,Lasso 在训练集与测试集上的表现都很差。这表示存在欠拟合,我们发现模型只用到了105 个特征中的4 个。与Ridge 类似,Lasso 也有一个正则化参数alpha,可以控制系数趋向于0 的强度。在这个例子中,我们用的是默认值alpha=1.0。为了降低欠拟合,我们尝试减小alpha。这么做的同时,我们还需要增加max_iter的值(运行迭代的最大次数):
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0)))
Training set score: 0.90
Test set score: 0.77
Number of features used: 33
alpha 值变小,我们可以拟合一个更复杂的模型,在训练集和测试集上的表现也更好。模型性能比使用Ridge 时略好一点,而且我们只用到了105 个特征中的33 个。这样模型可能更容易理解。
但如果把alpha设得太小,那么就会消除正则化的效果,并出现过拟合,得到与LinearRegression类似的结果:
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso00001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso00001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso00001.coef_ != 0)))
Training set score: 0.95
Test set score: 0.64
Number of features used: 96
对不同模型的系数进行作图,如下图:
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")
plt.plot(ridge01.coef_, "o", label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
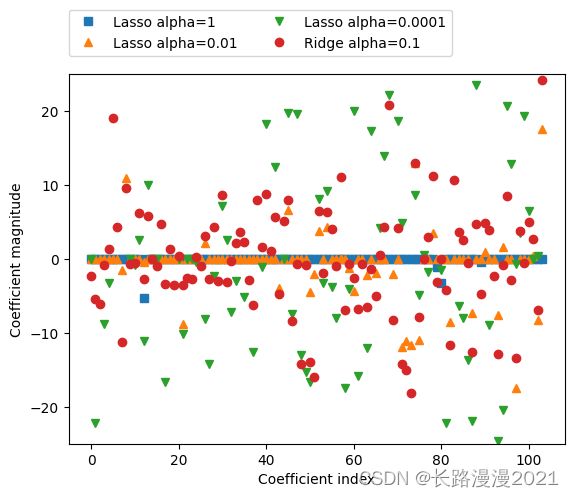
在alpha=1 时,我们发现不仅大部分系数都是0(我们已经知道这一点),而且其他系数也都很小。将alpha 减小至0.01,我们得到图中向上的三角形,大部分特征等于0。alpha=0.0001 时,我们得到正则化很弱的模型,大部分系数都不为0,并且还很大。为了便于比较,图中用圆形表示Ridge 的最佳结果。alpha=0.1 的Ridge 模型的预测性能与alpha=0.01 的Lasso 模型类似,但Ridge 模型的所有系数都不为0。
温馨提示: 在实践中,在两个模型中一般首选岭回归。但如果特征很多,你认为只有其中几个是重要的,那么选择Lasso可能更好。scikit-learn 还提供了ElasticNet类,结合了Lasso 和Ridge 的惩罚项。在实践中,这种结合的效果最好,不过代价是要调节两个参数:一个用于L1 正则化,一个用于L2 正则化。
补充:可以使用LassoCV类寻找最优alpha,详细了解,请阅读:sklearn.linear_model.LassoCV
2 用于分类的线性模型
对于用于回归的线性模型,输出ŷ 是特征的线性函数,是直线、平面或超平面(对于更高维的数据集)。对于用于分类的线性模型,决策边界是输入的线性函数。换句话说,(二元)线性分类器是利用直线、平面或超平面来分开两个类别的分类器。
学习线性模型有很多种算法。这些算法的区别在于以下两点:
- 系数和截距的特定组合对训练数据拟合好坏的度量方法;
- 是否使用正则化,以及使用哪种正则化方法。
不同的算法使用不同的方法来度量“对训练集拟合好坏”。由于数学上的技术原因,不可能调节 w \pmb{w} www 和 b b b 使得算法产生的误分类数量最少。对于这个目的,以及对于许多应用而言,上面第一点(称为损失函数)的选择并不重要。
最常见的两种线性分类算法是Logistic 回归(logistic regression)和线性支持向量机(linear support vector machine, 线性SVM), 前者在linear_model.LogisticRegression中实现,后者在svm.LinearSVC(SVC 代表支持向量分类器)中实现。
2.1 Logistic 回归
下面将LogisticRegression 和LinearSVC 模型应用到forge数据集上,并将线性模型找到的决策边界可视化
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X, y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
clf = model.fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{}".format(clf.__class__.__name__))
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
axes[0].legend()

对于LogisticRegression和LinearSVC, 决定正则化强度的权衡参数叫作C。C值越大,对应的正则化越弱。换句话说,如果参数C值较大,那么LogisticRegression和LinearSVC将尽可能将训练集拟合到最好,而如果C值较小,那么模型更强调使系数向量(w)接近于0。
参数C的作用还有另一个有趣之处。较小的C值可以让算法尽量适应“大多数”数据点,而较大的C值更强调每个数据点都分类正确的重要性。
mglearn.plots.plot_linear_svc_regularization()

在左侧的图中,C 值很小,对应强正则化。大部分属于类别0 的点都位于底部,大部分属于类别1 的点都位于顶部。强正则化的模型会选择一条相对水平的线,有两个点分类错误。在中间的图中,C 值稍大,模型更关注两个分类错误的样本,使决策边界的斜率变大。最后,在右侧的图中,模型的C 值非常大,使得决策边界的斜率也很大,现在模型对类别0中所有点的分类都是正确的。类别1 中仍有一个点分类错误,这是因为对这个数据集来说,不可能用一条直线将所有点都分类正确。右侧图中的模型尽量使所有点的分类都正确,但可能无法掌握类别的整体分布。换句话说,这个模型很可能过拟合。
在乳腺癌数据集上详细分析LogisticRegression:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42)
logreg = LogisticRegression().fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg.score(X_train, y_train))) # Training set score: 0.944
print("Test set score: {:.3f}".format(logreg.score(X_test, y_test))) # Test set score: 0.965
C=1 的默认值给出了相当好的性能,在训练集和测试集上都达到95% 的精度。但由于训练集和测试集的性能非常接近,所以模型很可能是欠拟合的。我们尝试增大C 来拟合一个更灵活的模型:
logreg100 = LogisticRegression(C=100).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg100.score(X_train, y_train))) # Training set score: 0.948
print("Test set score: {:.3f}".format(logreg100.score(X_test, y_test))) # Test set score: 0.958
使用C=100 可以得到更高的训练集精度,也得到了稍高的测试集精度,这也证实了我们的直觉,即更复杂的模型应该性能更好。
设置C=0.01:
logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg001.score(X_train, y_train))) # Training set score: 0.934
print("Test set score: {:.3f}".format(logreg001.score(X_test, y_test))) # Test set score: 0.930
此时,训练集和测试集的精度都比采用默认参数时更小。
最后,来看一下正则化参数C 取三个不同的值时模型学到的系数:
plt.plot(logreg.coef_.T, 'o', label="C=1")
plt.plot(logreg100.coef_.T, '^', label="C=100")
plt.plot(logreg001.coef_.T, 'v', label="C=0.01")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.ylim(-5, 5)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.legend()
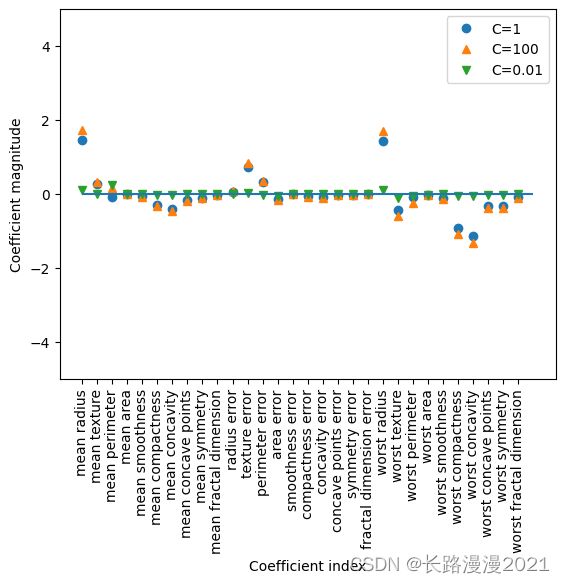
如果想要一个可解释性更强的模型,使用L1 正则化可能更好,因为它约束模型只使用少数几个特征。下面是使用L1 正则化的系数图像和分类精度:
for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):
lr_l1 = LogisticRegression(C=C, penalty="l1", solver="liblinear").fit(X_train, y_train)
print("Training accuracy of l1 logreg with C={:.3f}: {:.2f}".format(C, lr_l1.score(X_train, y_train)))
print("Test accuracy of l1 logreg with C={:.3f}: {:.2f}".format(C, lr_l1.score(X_test, y_test)))
plt.plot(lr_l1.coef_.T, 'v', label="C=0.01")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.ylim(-5, 5)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.legend()
Training accuracy of l1 logreg with C=0.001: 0.91
Test accuracy of l1 logreg with C=0.001: 0.92
Training accuracy of l1 logreg with C=1.000: 0.96
Test accuracy of l1 logreg with C=1.000: 0.96
Training accuracy of l1 logreg with C=100.000: 0.99
Test accuracy of l1 logreg with C=100.000: 0.98

与用于回归的线性模型一样,二分类的线性模型的主要差别在于penalty参数,这个参数会影响正则化,也会影响模型是使用所有可用特征还是只选择特征的一个子集。
2.2 线性支持向量机
下面是一个二维数据集,每个类别的数据都是从一个高斯分布中采样得出的
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])
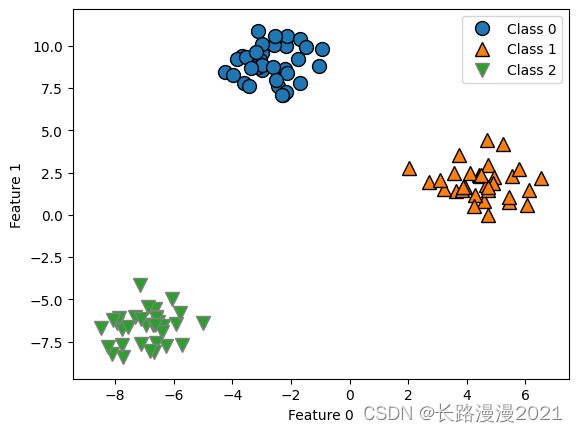
在这个数据集上训练一个LinearSVC分类器:
linear_svm = LinearSVC().fit(X, y)
print("Coefficient shape: ", linear_svm.coef_.shape) # Coefficient shape: (3, 2)
print("Intercept shape: ", linear_svm.intercept_.shape) # Intercept shape: (3,)
coef_ 的形状是(3, 2),说明coef_每行包含三个类别之一的系数向量,每列包含某个特征(这个数据集有2 个特征)对应的系数值。现在intercept_是一维数组,保存每个类别的截距。
将这3个二类分类器给出的直线可视化:
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1', 'Line class 2'], loc=(1.01, 0.3))

由图可以看到,训练集中所有属于类别0 的点都在与类别0 对应的直线上方,这说明它们位于这个二类分类器属于“类别0”的那一侧。属于类别0 的点位于与类别2 对应的直线上方,这说明它们被类别2 的二类分类器划为“其余”。属于类别0 的点位于与类别1 对应的直线左侧,这说明类别1 的二元分类器将它们划为“其余”。因此,这一区域的所有点都会被最终分类器划为类别0(类别0 的分类器的分类置信方程的结果大于0,其他两个类别对应的结果都小于0)。
但图像中间的三角形区域属于哪一个类别呢,3 个二类分类器都将这一区域内的点划为“其余”。这里的点应该划归到哪一个类别呢?答案是分类方程结果最大的那个类别,即最接近的那条线对应的类别。
下面的例子给出了二维空间中所有区域的预测结果:
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1', 'Line class 2'], loc=(1.01, 0.3))

小结
- 优点:
- 线性模型训练速度快,预测速度快,可以推广到非常大的数据集,也能应用于稀疏数据
- 线性模型更容易理解和解释
- 线性模型在高维空间中表现通常都很好
- 参数:
- 回归模型中为 alpha
- alpha 值较大时,模型简单
- 线性 SVM 分类模型和 Logistic 回归模型中为 C
- C 值较小时,模型简单
- 还可以控制正则化方式 penalty,默认为 L2,还可以设置 L1
- 回归模型中为 alpha
参考
- scikit-learn 线性回归算法库小结:https://www.cnblogs.com/pinard/p/6026343.html
- sklearn.linear_model.LassoCV:https://scikit-learn.org.cn/view/414.html