Generative Model - 李宏毅笔记
最近如火如荼AI绘画,原理上使用了一种新的算法Diffusion,叫扩散算法,它比起之前的对抗神经网络GAN,在做图像生成应用上,强的太多了。
以图像直方图为例,我们将图像中所有的像素值(0~255)按照频率统计绘制成直方图,这就是一张画像的像素分布
- 那用GAN去做AI绘画,生成出的一堆画像,可能这一堆画像风格、人物都是很相似的(这里就可以说他们是同一种分布的)
- 用Diffusion算法做的AI绘画,生成出的画像,可能就是不同类型,不同事物的,有画山水、画人物、有动漫、有素描等等。(他们为不同分布,分散),也因此这个算法叫扩散算法
再学习扩散算法之前,本文先从GAN算法开始展开学习。
Generative Model - 李宏毅笔记
- GAN
-
- Generator简介
- Discriminator简介
- 算法原理
-
- Generator loss
- Discriminator loss
-
- 判别器的损失函数优化问题
- 算法流程
- 数据分布问题
GAN
GAN的算法结构,是由一个生成器(Generator)和一个判别器(Discriminator)共同组成。它们之间的关系很相似食物链之间,又或者疫苗与新冠病毒之间,一种互相“对抗”下共同进化。
就像是数码宝贝一样,独角兽看成是生成器,暴龙兽看成是判别器,算法迭代的过程像是:
独角兽与暴龙兽对抗下,学习进化的过程
独角兽打不过暴龙兽,于是独角兽进化(生成器优化)
暴龙兽打不过加鲁鲁,于是暴龙兽进化(判别器进化)
。。。
战斗暴龙兽打不过钢铁加鲁鲁,(完结,二个数码兽通过对抗战斗都称为究极体)
这也就是对抗一词的由来,
GAN发展目前已经衍生出许多的变体:ACGAN、BGAN、CGAN、DCGAN等等
下面将分别对生成器和判别器展开介绍
Generator简介
普通的卷积神经网络,通常输入和输出是,1对1,或者多对1的。
以视频预测应用举例:我们向模型传入视频前几帧的图像,模型预测输出下一帧的图像。
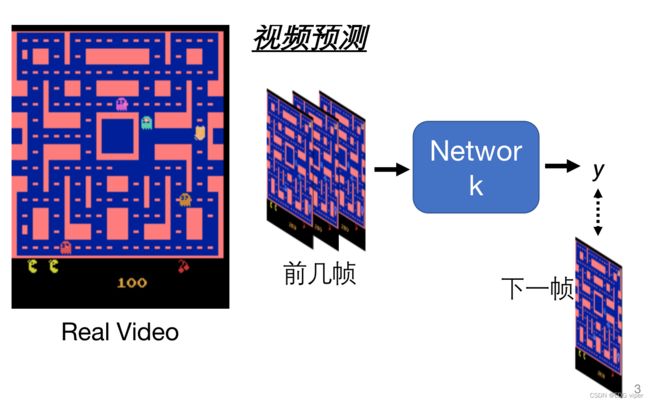
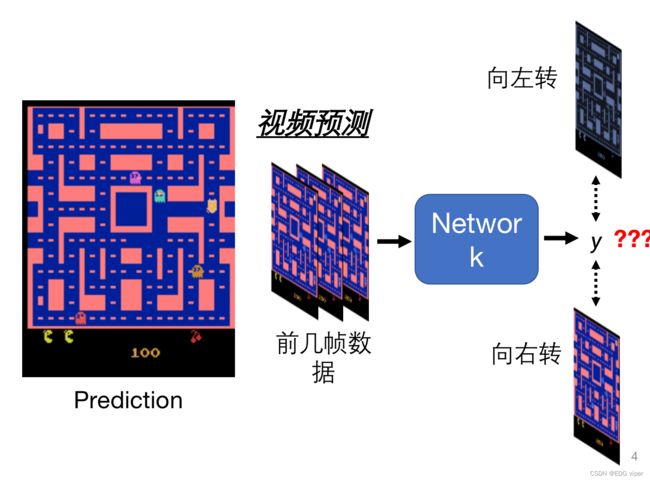
但是生成器模型中,我们向模型传入视频前几帧的图像,模型会预测输出不同的下一帧图像(向左转,向右转,向上转,向下转),这就是生成器模型独特的创新性。
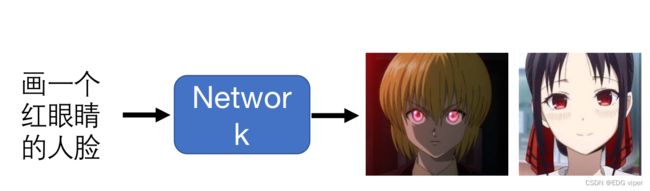
生成器的创新能力,就像是绘画一样,虽然老师要求是画一个红眼睛的动漫人,但是每个学生画出来的人物都是不一样的
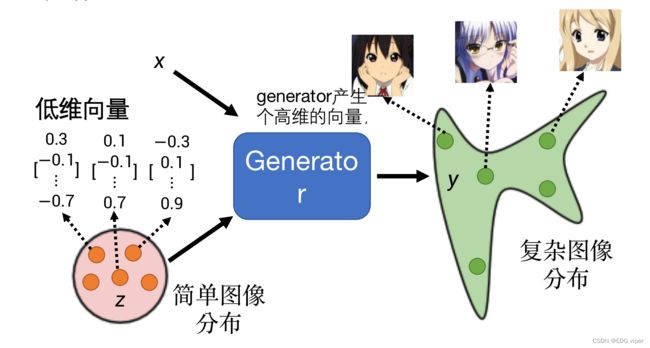
假设Z代表一堆简单的低维向量,一堆向量加入到生成器,在生成器中进行一些卷积操作,输出一个图像(一种图像分布),
我们如果让低维向量乘以255,是不是可以得到一个RBG通道下的像素图像。可以推理猜想到,生成器网络中就是把这些低维的图像,疯狂组合,组合成人脸的头像。
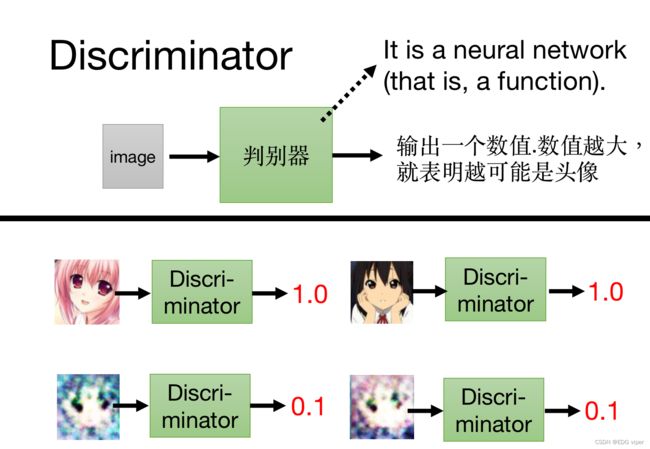
Discriminator简介
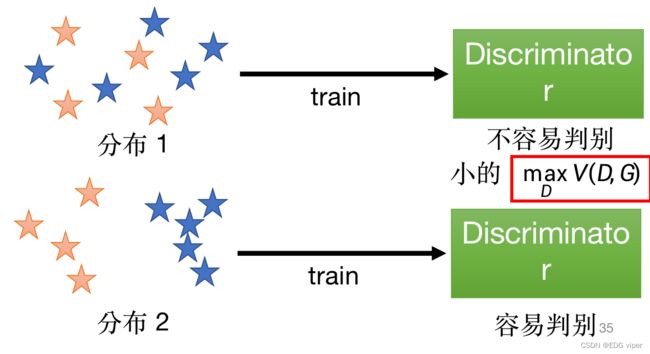
判别器像是一个打分的函数,基于生成器生成的图像进行打分,输出的数值越接近1,表明生成器效果也好。
算法原理
Generator loss
生成器通过定义一个loss function损失函数,使其loss最小化,从而达到优化生成器的目的,定义判别器网络,也是通过一个loss function损失函数,来优化判别器,不过与之不同的是,判别器的loss,是尽可能使其最大化。
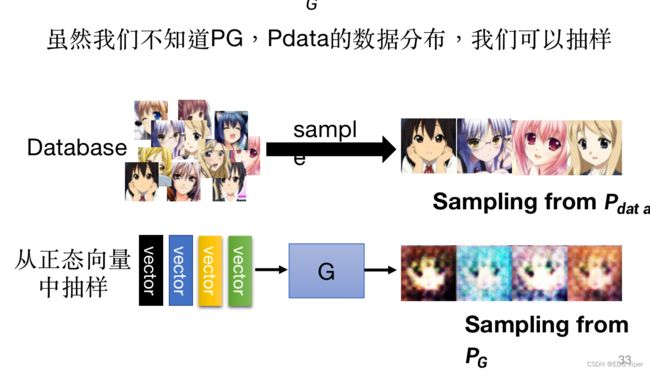
比如下图所示:我们将一些简单分布的一维向量作为输入,输入到生成器中,生成器产生一些复杂分布的一维向量( P G P_G PG),求 P G P_G PG与真实的向量 P d a t a P_{data} Pdata的差异,也就是计算生成器的loss, D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata),使其差异最小化 G = a r g m i n D i v ( P G , P d a t a ) G=argmin Div(P_G,P_{data}) G=argminDiv(PG,Pdata)
这里的最小化函数就是我们定义的loss function
如何去计算这个Div,我们可以通过抽样的方法,得到真实图像的样本 P d a t a P_{data} Pdata,和生成器输出的图像样本 P G P_G PG,计算二者图像之间的像素差异来实现Div。
Discriminator loss
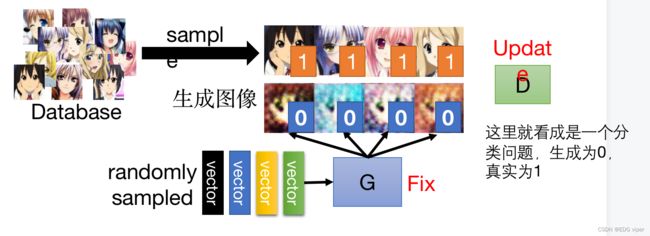
判别器模型:将生成器生成的数据class 2 和真实数据class 1 ,加入到判别器模型中,判别器模型类似于一个逻辑回归的二分类模型,判别器能根据输入的图像数据,分别出那个图像是class 1,那个图像是class 2。
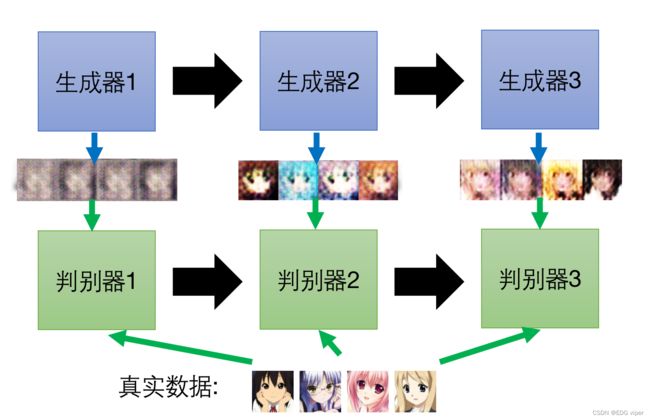
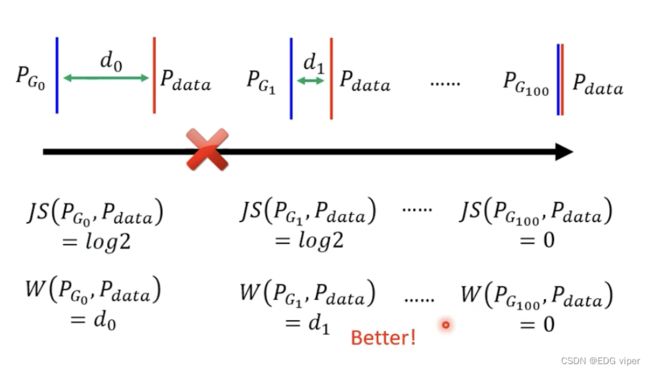
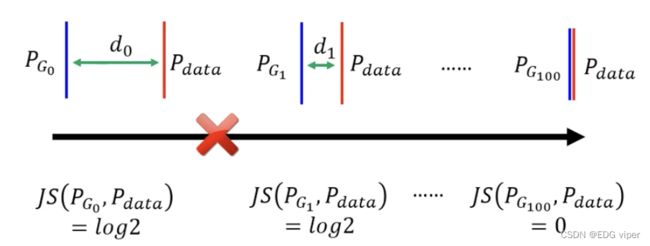
在二分类中模型输出一个[0,1]范围的值y 对比二分类模型可以知道,在判别器模型中,模型的参数优化目的,是希望将真实数据输入模型,模型预测输出的y值尽可能趋近1,将生成器数据输入,模型预测出的y值尽可能趋近0。 E y − P d a t a ∗ l o g ( D ( y ) ) E_{y-P_{data}}*log(D(y)) Ey−Pdata∗log(D(y)):真实数据的loss 之前提到过判别器与生成器是一个对抗的过程,判别器应该是能有效的分别出生成器的数据的,也就是说,生成器的数据 类别是class 2,那模型预测生成器的数据 预测出的类别也应该都是class 2。 所以判别器的损失函数对于生成器数据的loss,应该越小越好,那与之对应下,真实数据的loss,就会越来越大,最后真实数据loss与生成器数据的loss相加,其实整体的loss是越来越大的。我们求解判别器问题,就是希望判别器的损失函数最大化 回到输入到判别器的数据中 了解完生成器和判别器的损失计算,不难发现,似乎都是利用生成数据 P G P_{G} PG和真实数据 P d a t a P_{data} Pdata之间的差异距离来实现的,只不过生成器是计算是最小值,判别器计算的是最大值 因此可以把生成器和判别器的损失函数合并为 G ∗ G^* G∗ 首先初始化生成器与判别器的参数 Step1:先固定住生成器的参数,更新判别器的参数 下图展示了一个头像生成应用,经历多次迭代更新的过程 生成器的数据是通过抽样获得的,所以在大多数情况,一开始生成器生成出的数据通常与真实数据的数据分布是不同的,有很大差异,假设这个差异为 d 0 d_0 d0 在将数据导入到判别器进行训练,模型能够很容易的实现正确预测,因此其损失函数值是没有的(因为全部都预测正确),这里暂且认为是 l o g 2 log2 log2。 在下次迭代下,生成器生成的数据,与真实数据差异距离减小,虽然减少,但是还是有明显的差异的,这时判别器预测可能是全部正确的,所以它的损失函数值还是 l o g 2 log2 log2, 如果两个分布不重叠,二值分类器将达到100%的准确率。在训练期间,准确度(或损失)毫无意义。那这样的判别器迭代更新参数是无效意义的。 我们要做的就是,去掉生成器这种无意义的减少 P G P_G PG与 P d a t a P_{data} Pdata差异的迭代更新参数步骤,使生成器迭代更新每一步有价值,也就是需要求出有价值的差异距离 d d d 方法:
当y>value 时,类别为1
当y
在二分类模型中,二分类损失函数计算公式:
L = − y ∗ l o g ( p ) − ( 1 − y ) ∗ l o g ( 1 − p ) L=-y*log(p)-(1-y)*log(1-p) L=−y∗log(p)−(1−y)∗log(1−p)
由二分类损失函数换算到判别器中的损失函数为:
E y − P d a t a ∗ l o g ( D ( y ) ) + E y − P G ∗ ( l o g ( 1 − D ( y ) ) E_{y-P_{data}}*log(D(y))+E_{y-P_{G}}*(log(1-D(y)) Ey−Pdata∗log(D(y))+Ey−PG∗(log(1−D(y))
E y − P G ∗ ( l o g ( 1 − D ( y ) ) E_{y-P_{G}}*(log(1-D(y)) Ey−PG∗(log(1−D(y)):生成器数据的loss判别器的损失函数优化问题
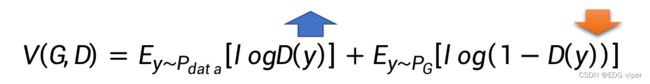
a r g m a x V ( G , D ) argmaxV(G,D) argmaxV(G,D)
G ∗ = a r g m i n ( m a x V ( G , D ) ) G^*=argmin(maxV(G,D)) G∗=argmin(maxV(G,D))算法流程
在每次训练迭代中:
Step2:固定住判别器的参数,更新生成器的参数
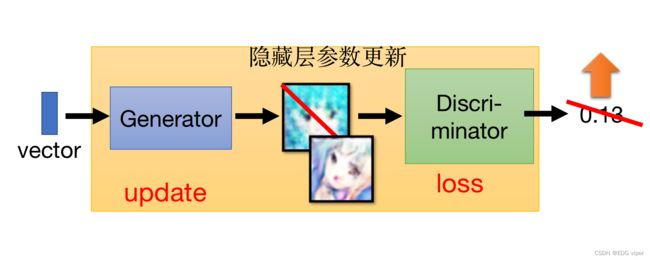
Step3:反复迭代step1、step2
100更新
1000 更新
5000 更新
50000 更新
数据分布问题
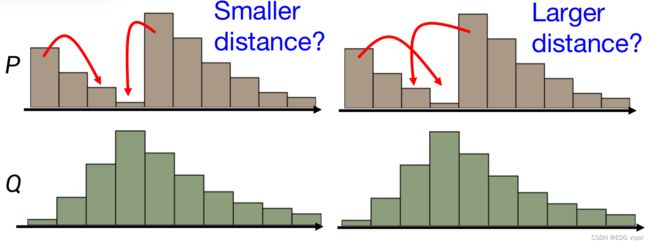
假设P为我们的生成数据,Q为真实数据,如何将P转变为Q的样子,可能会有很多种方法,穷举出所有搬移的方法,计算每种搬移的平均搬移距离,最后取平均搬移距离最小的方法,作为生成器参数的更新