过度拟合
Let us consider that we are designing a machine learning model. A model is said to be a good machine learning model, if it generalizes any new input data from the problem domain in a proper way. This helps us to make predictions in the future data, that data model has never seen. Now, suppose we want to check how well our machine learning model learns and generalizes to the new data. For that we have over fitting and under fitting, which are majorly responsible for the poor performances of the machine learning algorithms.
让我们考虑一下,我们正在设计一个机器学习模型。 如果模型以适当的方式归纳了来自问题域的任何新输入数据,则该模型被认为是很好的机器学习模型。 这有助于我们对数据模型从未见过的未来数据做出预测。 现在,假设我们要检查机器学习模型对新数据的学习和推广情况。 为此,我们过度拟合和不足拟合,这主要是造成机器学习算法性能不佳的原因。
Underfitting:
不足:
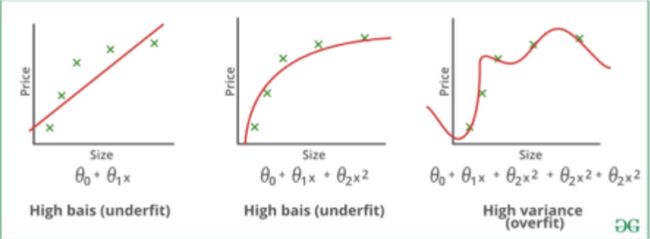
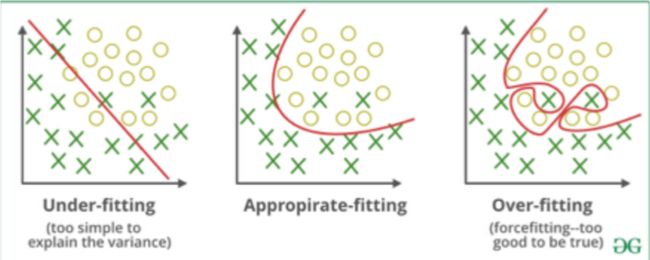
A statistical model or a machine learning algorithm is said to have underfitting when it cannot capture the underlying trend of the data. (It’s just like trying to fit undersized pants!) Underfitting destroys the accuracy of our machine learning model. Its occurrence simply means that our model or the algorithm does not fit the data well enough. It usually happens when we have less data to build an accurate model and also when we try to build a linear model with a non-linear data. In such cases the rules of the machine learning model are too easy and flexible to be applied on such a minimal data and therefore the model will probably make a lot of wrong predictions. Underfitting can be avoided by using more data and also reducing the features by feature selection.
当统计模型或机器学习算法无法捕获数据的潜在趋势时,则称该模型不合适。 (这就像试图穿上小号的裤子一样!)穿着不足会破坏我们的机器学习模型的准确性。 它的出现仅意味着我们的模型或算法不足以很好地拟合数据。 当我们使用较少的数据来构建准确的模型时,以及尝试使用非线性数据来构建线性模型时,通常会发生这种情况。 在这种情况下,机器学习模型的规则过于简单和灵活,无法应用于如此少的数据,因此该模型可能会做出很多错误的预测。 可以通过使用更多数据来避免拟合不足,并且还可以通过特征选择来减少特征。
Overfitting:
过度拟合:
A statistical model is said to be overfitted, when we train it with a lot of data (just like fitting ourselves in an oversized pants!). When a model gets trained with so much of data, it starts learning from the noise and inaccurate data entries in our data set. Then the model does not categorize the data correctly, because of too much of details and noise. The causes of overfitting are the non-parametric and non-linear methods because these types of machine learning algorithms have more freedom in building the model based on the dataset and therefore they can really build unrealistic models. A solution to avoid overfitting is using a linear algorithm if we have linear data or using the parameters like the maximal depth if we are using decision trees.
当我们用大量数据训练统计模型时,该模型被认为是过拟合的(就像将自己放入一条超大号裤子一样!)。 当一个模型接受了如此大量的数据训练后,便开始从噪声和数据集中不准确的数据条目中学习。 然后,由于过多的细节和噪音,该模型无法正确地对数据进行分类。 过度拟合的原因是非参数和非线性方法,因为这些类型的机器学习算法在基于数据集构建模型时具有更大的自由度,因此它们实际上可以构建不切实际的模型。 避免过度拟合的解决方案是,如果我们具有线性数据,则使用线性算法;如果使用决策树,则使用诸如最大深度之类的参数。
How to avoid Overfitting:
如何避免过度拟合:
The commonly used methodologies are:
常用的方法是:
Cross- Validation:
交叉验证:
A standard way to find out-of-sample prediction error is to use 5-fold cross validation.
查找样本外预测误差的标准方法是使用5倍交叉验证。
Early Stopping:
提前停止:
Its rules provide us the guidance as to how many iterations can be run before learner begins to over-fit.
它的规则为我们提供了有关在学习者开始过度适应之前可以运行多少次迭代的指导。
Pruning:
修剪:
Pruning is extensively used while building related models. It simply removes the nodes which add little predictive power for the problem in hand.
在建立相关模型时,修剪被广泛使用。 它只是删除了对手头的问题几乎没有增加预测能力的节点。
Regularization:
正则化:
It introduces a cost term for bringing in more features with the objective function. Hence it tries to push the coefficients for many variables to zero and hence reduce cost term
它引入了一个成本术语,以引入具有目标功能的更多功能。 因此,它试图将许多变量的系数推为零,从而降低成本项
Good Fit in a Statistical Model:
非常适合统计模型:
Ideally, the case when the model makes the predictions with 0 error, is said to have a good fit on the data. This situation is achievable at a spot between overfitting and underfitting. In order to understand it we will have to look at the performance of our model with the passage of time, while it is learning from training dataset. With the passage of time, our model will keep on learning and thus the error for the model on the training and testing data will keep on decreasing. If it will learn for too long, the model will become more prone to overfitting due to presence of noise and less useful details. Hence the performance of our model will decrease. In order to get a good fit, we will stop at a point just before where the error starts increasing. At this point the model is said to have good skills on training dataset as well our unseen testing dataset.
理想情况下,模型预测误差为0的情况被认为非常适合数据。 这种情况可以在过拟合和欠拟合之间实现。 为了理解它,我们必须随着时间的流逝来观察我们模型的性能,而它是从训练数据集中学习的。 随着时间的流逝,我们的模型将继续学习,因此该模型在训练和测试数据上的误差将不断减少。 如果学习时间太长,由于存在噪音和有用的细节较少,该模型将更容易过度拟合。 因此,我们模型的性能将下降。 为了获得良好的拟合度,我们将在误差开始增加之前的某个位置停止。 在这一点上,该模型在训练数据集以及我们看不见的测试数据集方面具有良好的技能。
Introduction to Dimensionality Reduction
降维简介
In statistics, machine learning, and information theory, dimensionality reduction or dimension reduction is the process of reducing the number of random variables under consideration by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.
在统计,机器学习和信息论中,降维或降维是通过获取一组主变量来减少所考虑的随机变量数量的过程。 它可以分为特征选择和特征提取。
Machine Learning:
机器学习:
As discussed in this article, machine learning is nothing but a field of study which allows computers to “learn” like humans without any need of explicit programming.
如本文所述,机器学习不过是一个研究领域,它使计算机可以像人类一样“学习”,而无需任何显式编程。
What is Predictive Modeling:
什么是预测建模:
Predictive modeling is a probabilistic process that allows us to forecast outcomes, on the basis of some predictors. These predictors are basically features that come into play when deciding the final result, i.e. the outcome of the model.
预测建模是一个概率过程,可让我们在某些预测因子的基础上预测结果。 这些预测器基本上是在决定最终结果(即模型的结果)时起作用的功能。
Dimensionality Reduction
降维
In machine learning classification problems, there are often too many factors on the basis of which the final classification is done. These factors are basically variables called features. The higher the number of features, the harder it gets to visualize the training set and then work on it. Sometimes, most of these features are correlated, and hence redundant. This is where dimensionality reduction algorithms come into play.
在机器学习分类问题中,通常会根据太多因素进行最终分类。 这些因素基本上是称为特征的变量。 功能数量越多,越难以可视化训练集,然后对其进行处理。 有时,大多数这些功能都是相关的,因此是多余的。 这是降维算法发挥作用的地方。
Dimensionality reduction is the process of reducing the number of random variables under consideration, by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.
降维是通过获取一组主变量来减少所考虑的随机变量数量的过程。 它可以分为特征选择和特征提取。
Dimensionality Reduction important in Machine Learning and Predictive Modeling
降维在机器学习和预测建模中很重要
An intuitive example of dimensionality reduction can be discussed through a simple email classification problem, where we need to classify whether the e-mail is spam or not. This can involve a large number of features, such as whether or not the e-mail has a generic title, the content of the e-mail, whether the e-mail uses a template, etc. However, some of these features may overlap. In another condition, a classification problem that relies on both humidity and rainfall can be collapsed into just one underlying feature, since both of the aforementioned are correlated to a high degree. Hence, we can reduce the number of features in such problems. A 3-D classification problem can be hard to visualize, whereas a 2-D one can be mapped to a simple 2 dimensional space, and a 1-D problem to a simple line. The below figure illustrates this concept, where a 3-D feature space is split into two 1-D feature spaces, and later, if found to be correlated, the number of features can be reduced even further.
降维的直观示例可以通过一个简单的电子邮件分类问题来讨论,在该问题中,我们需要对电子邮件是否为垃圾邮件进行分类。 这可能涉及许多功能,例如电子邮件是否具有通用标题,电子邮件的内容,电子邮件是否使用模板等。但是,其中某些功能可能会重叠。 在另一种情况下,依赖于湿度和降雨的分类问题可以被分解为一个基本特征,因为上述两个方面都高度相关。 因此,我们可以减少此类问题中的特征数量。 3-D分类问题可能很难可视化,而2-D分类问题可以映射到简单的二维空间,而1-D问题可以映射到简单的线。 下图说明了此概念,其中将3-D特征空间划分为两个1-D特征空间,然后,如果发现存在关联,则可以进一步减少特征数量。
There are two components of dimensionality reduction:
降维有两个组成部分:
Feature selection:
功能选择:
In this, we try to find a subset of the original set of variables, or features, to get a smaller subset which can be used to model the problem. It usually involves three ways:
在这种情况下,我们尝试找到原始的变量集或特征集的子集,以获得较小的子集,该子集可用于对问题进行建模。 它通常涉及三种方式:
1. Filter
1.筛选
2 .Wrapper
2。包装
3 .Embedded
3。嵌入式
Feature extraction:
特征提取:
This reduces the data in a high dimensional space to a lower dimension space, i.e. a space with lesser no. of dimensions.
这将高维空间中的数据减少到低维空间,即编号较小的空间。 尺寸。
Methods of Dimensionality Reduction
降维方法
The various methods used for dimensionality reduction include:
用于降维的各种方法包括:
- Principal Component Analysis (PCA) 主成分分析(PCA)
- Linear Discriminant Analysis (LDA) 线性判别分析(LDA)
- Generalized Discriminant Analysis (GDA) 广义判别分析(GDA)
Dimensionality reduction may be both linear or non-linear, depending upon the method used. The prime linear method, called Principal Component Analysis, or PCA, is discussed below.
降维可以是线性的,也可以是非线性的,具体取决于所使用的方法。 以下讨论了称为主成分分析(PCA)的素线性方法。
Principal Component Analysis
主成分分析
This method was introduced by Karl Pearson. It works on a condition that while the data in a higher dimensional space is mapped to data in a lower dimension space, the variance of the data in the lower dimensional space should be maximum.
此方法由Karl Pearson提出。 它的工作条件是,将高维空间中的数据映射到低维空间中的数据时,低维空间中的数据方差应该最大。
It involves the following steps:
它涉及以下步骤:
- Construct the covariance matrix of the data. 构造数据的协方差矩阵。
- Compute the eigenvectors of this matrix. 计算此矩阵的特征向量。
- Eigenvectors corresponding to the largest eigenvalues are used to reconstruct a large fraction of variance of the original data. Hence, we are left with a lesser number of eigenvectors, and there might have been some data loss in the process. But, the most important variances should be retained by the remaining eigenvectors. 对应于最大特征值的特征向量用于重构原始数据的很大一部分方差。 因此,我们只剩下较少的特征向量,并且在此过程中可能会丢失一些数据。 但是,最重要的方差应保留在其余特征向量中。
Advantages of Dimensionality Reduction
降维的优势
• It helps in data compression, and hence reduced storage space.
•它有助于数据压缩,因此减少了存储空间。
- It reduces computation time. 它减少了计算时间。
- It also helps remove redundant features, if any. 它还有助于删除多余的功能(如果有)。
Disadvantages of Dimensionality Reduction
降维的缺点
• It may lead to some amount of data loss.
•这可能会导致一定程度的数据丢失。
- PCA tends to find linear correlations between variables, which is sometimes undesirable. PCA倾向于发现变量之间的线性相关性,这有时是不可取的。
- PCA fails in cases where mean and covariance are not enough to define datasets. 如果均值和协方差不足以定义数据集,则PCA失败。
- We may not know how many principal components to keep- in practice, some thumb rules are applied. 我们可能不知道要实践多少个主要组成部分,但要应用一些经验法则。
翻译自: https://medium.com/analytics-vidhya/the-ultimate-guide-of-over-fitting-under-fitting-and-dimensionality-reduction-28f44f632768
过度拟合