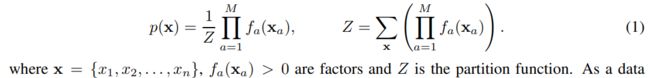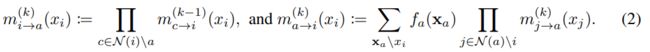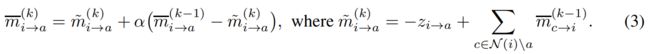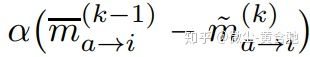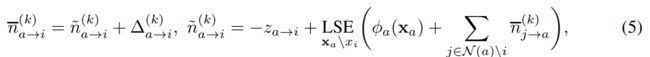BPNN-Belief Propagation Neural Networks
https://arxiv.org/pdf/2007.00295
经验丰富的神经求解器已成功用于解决组合优化和决策问题。 但是,这些问题的更一般的计数变体仍在很大程度上由手工求解器解决。 为弥合这一差距,我们引入了信念传播神经网络(BPNN),这是一类对因子图进行操作并推广信念传播(BP)的参数化运算符。 在最严格的形式下,BPNN层(BPNN-D)是一个有经验的迭代算子,可证明为任何参数选择都能保持BP的许多理想特性。 从经验上讲,我们表明BPNN-D可比原始BP更好地执行任务:前者在Ising模型上收敛速度快1.7倍,同时提供了更严格的界限。 在很有挑战性的模型计数问题上,BPNN的计算速度比最先进的手工方法快100倍,同时还返回了可比质量的估算值。
1 Introduction
从统计物理学到机器学习,概率推断问题出现在许多领域。
人们几乎没有希望找到有效,准确的解决方案,因为它们至少与NP完全决策问题一样困难(这里吐槽下,设A为constraint programing,B为belief propagation,C为combinatorial optimization,我看到一小堆文章用A/B助力C,或用A/C助力B,或用B/C助力A,总之三者互相兜圈子)。 机器学习,统计和统计物理学领域已进行了大量研究,以开发基于变分和采样的方法来近似这些挑战性问题[13、34、48、6、38]。 由于进行了广泛的理论分析,诸如信念传播(BP)[31]之类的变分方法在提供原理近似值方面尤为成功。
我们介绍了信念传播神经网络(BPNN),这是一种灵活的神经体系结构,旨在估计因子图的分配/分区函数。 BPNN可以对BP进行广义化,因此当在少量具有已知分区函数的因子图上进行训练时,BPNN可以提供比BP更准确的估计。 同时,BPNN保留了BP的许多属性,与常规神经体系结构相比,这可以使估算更为准确。 BPNN由迭代层(BPNND)和可选的Bethe自由能层(BPNN-B)组成,两者在因子图同构下均保持BP的对称性。 BPNN-D是参数化的迭代算子,它在保留许多BP保证的同时严格地概括BP。 像BP一样,BPNN-D可保证收敛于树形结构的因子图并返回精确的分区函数。 对于具有循环的因子图,只要从BP不动点获得的Bethe逼近是可证明的下界(对BPNN-D有轻微限制),BPNN-D就会计算下界。 BPNN-B执行从信念的轨迹(经过固定的迭代次数)到输入因子图的分区函数的回归。 尽管这牺牲了一些保证,但BPNN-B引入的额外灵活性通常会提高估计性能。
实验表明,在Ising模型上,BPNN-D的收敛速度比标准BP更快,并且经常可以提供更严格下界的更好不动点。 BPNN-D可以很好地推广到从与训练期间不同的分布中采样的Ising模型以及具有比训练期间几乎两倍的变量的模型,从而提供对数分区函数的估计,其明显优于BP或标准图神经网络 (GNN)。 我们还针对社区检测问题进行了实验,其中BP在经验上和理论上都表现出色,并显示了对BP和标准GNN的改进。 然后,我们在近似模型计数[46、27、28、8]上进行实验,这是计算布尔可满足性(SAT)问题的解数的问题。 与前两个实验不同,BP在这种情况下很难收敛。 尽管如此,我们发现BPNN可以从10个问题的训练集中学习估计准确的模型计数,并将其推广到对于确切的模型计数器而言很难解决的问题。 与手工制作的近似模型计数器相比,BP使用GPU计算返回的可比估计速度快了100倍。
2 Background: Factor Graphs and Belief Propagation
因子图是离散概率分布的表示形式。 信念传播是一种近似因子图的归一化常数或分区函数的方法。 令p(x)是根据因子图定义的离散概率分布
因子图是具有n个变量节点和M个因子(看成一撮变量节点的函数就好)节点的二部图。 仅当变量在因子的定义域内时,因子节点和变量节点才连接。
信念传播
信念传播执行相邻变量和因子节点间的迭代消息传递。 在第k次迭代时,变量-因子消息 ![]() ,因子-变量消息
,因子-变量消息![]() 的计算为
的计算为
消息通常随机或初始化为常量。BP算法估计与每个因子 相关的变量集合 的近似边际概率。 同样,BP计算每个变量的信念为
信念传播算法通过迭代更新变量因子消息和因子变量消息直到它们收敛到固定值(等式2的不动点)或达到预定义的最大迭代次数。 此时,信念用于计算因子图分区函数的变分近似。 这种近似最初是由统计物理学开发的,被称为Bethe自由能
数值稳定的信念传播
为了实现数值稳定性,通常在对数空间中执行信念传播,并且每次迭代都将消息标准化。 通常还添加一个阻尼参数α∈[0,1),以通过采取部分更新步骤来提高收敛性。 当α= 0时恢复无阻尼BP,α= 1则对应于不更新消息。
同样,来自等式2的因子变量被重写为
3 Belief Propagation Neural Networks
我们将信念传播神经网络(BPNN)设计为在因子图上运行的一系列图神经网络。 与标准图神经网络(GNN)不同,BPNN不会在节点之间重新发送消息从而避免“重复计算”,这是从BP获得的一种属性。此属性保证下面描述的BPNN-D在树上是正确的(定理3)。 BPNN-D是BP的严格泛化(命题1),但仍能保证通过寻找BP的不动点(定理2),在收敛后给出一类因子图的分割函数下界(定理3)。和BP一样,BPNN保留因子图固有的对称性(定理4)。
BPNN由两部分组成。 首先,迭代BPNN层输出消息,类似于标准BP。这些消息用于使用与BP相同的公式来计算信念。 其次,将信念传递到Bethe自由能层(BPNN-B)中,该层通过执行从信念到Z的回归来概括Bethe近似。或者,当使用标准Bethe近似代替BPNN-B时,BPNN提供了许多 BP的保证。
BPNN迭代层
BPNN迭代层是灵活的神经运算符,可以以多种方式对信念或消息进行操作。 (这块很重要!!!修改BPNN主要看这儿!!!)在这里,由于强大的收敛性,我们将重点放在特定变体BPNN-D上,读者可见附录C以获取其他变体的信息。 BPNN迭代阻尼层(BPNN-D)使用学习到的算子H的输出修改因子变量消息(公式4):
代替传统的阻尼项
其中di表示度,| Xi | 变量Xi的基数。 算法学习到的算子H(·)将每个因子变量消息的第k-1次迭代和第k次迭代间的差作为输入,并共同修改这些差。 因此,它可比标量乘法器丰富得多。 BPNN-D的因子-变量消息由下式给出
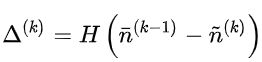 表示将H(·)应用于所有因子-变量消息差的结果,
表示将H(·)应用于所有因子-变量消息差的结果, 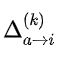 是与修改后的a→i消息差相对应的输出。
是与修改后的a→i消息差相对应的输出。
变量-因子消息与式3基本相同:
请注意,如果H是elementwise的,即H(x)=αx,我们将完全恢复方程式3和4。因此:
Proposition 1. BPNN-Ds将BP和阻尼BP归纳为一个严格的泛化。
对于H(·)的非平凡选择,事实证明BPNN是保留BP的不动点还是引入新的不动点,仅取决于H(·)本身的不动点集,即{x | H(x)= x}。 如下所示,此属性使我们可轻松强制BP的每个不动点也是BPNN-D的不动点(定理1),反之亦然(定理2)。(证明见附录A)
定理1.如果零是H(·)的一个不动点,那么BP的每个不动点也是BPNN-D的一个不动点。
定理2. 如果H(·)没有不为零的不动点,则BPNN-D的每个不动点也是BP的不动点。
结合定理1和定理2,我们得出推论2.1。
推论2.1. 如果零是H(·)的唯一不动点,则BP和BPNN-D的不动点相同。
请注意,一大类具有高表现力的可学习算子是可逆的[7]。强制BPNN-D的每个定点也是BP的定点是特别有用的,因为紧接着,只要从BP的定点得到的Bethe近似返回一个可证明的下界,BPNN-D就会返回一个下界(定理3)。当BPNN-D层迭代应用直至收敛时,对于树状结构的因子图,我们可保证快速收敛(命题2)。
如前所述,BPNN迭代层是灵活的,可另外修改为直接对消息值或因子信念进行操作,代价是不再返回下界(见附录C)。
定理3. 如果零是H(-)的唯一不动点,则从BPNN-D的不动点的信念计算出的Bethe近似(1)对于树形结构图是精确的,并且(2) lower bounds了任何具有二元变量和对数上势函数的因子图的分区函数。
命题2. 在高度为ℓ的树形结构因子图上,BPNN-D在ℓ次迭代内收敛。
Bethe自由能层(BPNN-B)
当不需要收敛到不动点时,我们可通过不共享权重的迭代层构建K层BPNN,从而提高体系结构的灵活性。 此外,我们使用两个MLP定义了Bethe自由能层(BPNN-B,等式7),该MLP将从每个因子和变量获取的信念的轨迹作为输入和输出标量:
此参数化包含标准Bethe逼近,因此我们可以初始化f_BPNN的参数以输出根据最终层信念计算得出的Bethe逼近(有关详细信息,请参见附录)。 注意| xa | 是因子a范围内的变量数,S | xa | 表示对称组({1、2,...,| xa |}的所有排列),排列σ应用于所有2k串联项的维数。 我们通过将所有因子的信念传递给MLP__BF并对结果求平均值,从而确保BPNN保留BP的对称性(定理4)。
BPNN保留BP的对称性
BPNN的设计使等效输入因子图映射到等效输出。 这是BP默认满足的属性。 标准GNN也被设计为满足此属性,但是,图之间的“等效性”概念不同于因子图间的“等效性”概念。 在本节中,我们将这些声明形式化。
图同构定义了标准GNN遵守的图之间的等价关系。 如果节点适当匹配,则两个同构图在结构上是等效的,并且无法区分。 更正式地说,在两个图中节点(或其索引)之间存在双射,从而定义了这种匹配。标准GNN的设计使输出节点表示与输入节点索引等价;输出节点表示的索引与输入节点的索引匹配。在两个同构图上运行的GNN的输出节点表示可以使用定义同构的同一个偏置来匹配。 此外,标准的GNN被设计为将同构图映射到相同的图级输出表示。 这两个属性是通过使用消息聚合函数和图级输出函数来实现的,这两个函数对于节点索引都是不变的。
我们在定义1(附录A)中正式定义因子图同构。 这种等效关系比标准图更复杂,因为因子势定义了因子和变量节点之间的结构化关系。 如在标准图中,在因子图的表示形式中,变量节点被全局索引(X1,X2,...,Xn)。 此外,变量节点还通过包含变量节点的因子在本地进行索引。 这是必需的,因为每个因子维度(请注意因子是张量)都对应一个唯一变量,除非因子碰巧是对称的。 局部变量索引定义了因子维数和变量的全局索引之间的映射。 这些局部变量索引会导致同构因子图的定义中出现其他双射(定义1中的条件2)。 请注意,由于这些额外的双射,标准GNN不遵守因子图同构。
与标准GNN相比,BP遵守因子图的同构性。 当BP在恒定消息初始化的两个同构因子图上进行相同数量的迭代时,输出信念和消息满足与输入因子图对应的双射。
具体来说,消息与全局节点索引(Lemma 1)等价,变量信念与全局变量节点索引(Lemma 2)等价,因子信念与全局因子节点索引和因子内局部变量节点索引等价(Lemma 3)。 我们将以上特性称为因子图同构下的BP等方差。 我们证明,当H(·)与全局节点索引等价时,这些属性也适用于BPNN-D。 当使用恒定消息初始化进行相同数量的迭代运行BP时,从同构因子图获得的Bethe逼近是相同的。 BPNN-B也满足此属性,因为根据设计,它对于因子内的局部变量索引是不变的(引理4)。 这些特性加在一起得出以下定理:
定理4. 如果H(-)对全局节点索引是等价的,那么(1)BPNN-D消息和信念在因子图同构下保留了BP的等价性,(2)BPNN-B在因子图同构下是不变的。
4 Experiments
我们训练了BPNN来估计来自多个域的因子图的分配/分区函数。 首先,在综合Ising模型上进行的实验表明,BPNN-D可学习找到比BP更好的不动点,并且收敛更快。 此外,BPNN对Ising模型进行泛化,其变量几乎是训练期间所见变量的两倍(这些变量是从不同分布中采样的)。 其次,通过社区检测对随机块模型进行的实验和消融研究表明,与标准GNN相比,在BPNN中保持BP的属性可以改善结果。 最后,在真实世界的SAT问题上进行的模型计数实验表明,BPNN可以从10’s of training problems中学习,泛化到对精确模型计数器来说比较困难的问题,并且计算估计值的速度比手工制作的近似模型计数器快100倍。我们使用 PyTorch Geometric[19]实现了 BPNN 和 GNN。关于GNN的细节,请参考附录B.2。
改进的下界和更快的收敛性
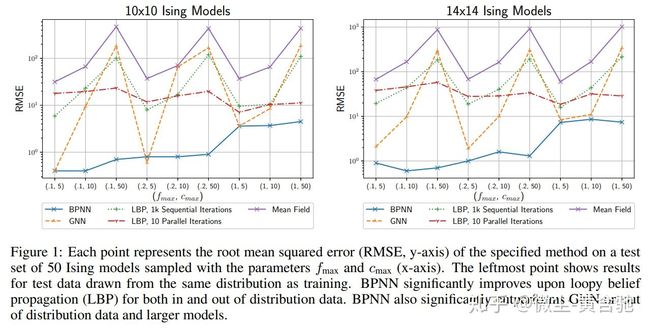
我们训练了一个迭代BPNN-D层,以在50个大小为10x10(100个变量)的随机Ising模型的训练集上下限划分函数的下限。 (有关更多详细信息,请参阅附录)然后,我们在50个Ising模型的验证集上运行了所学的BPNN-D和标准BP。 我们凭经验验证了BPNN-D找到了比BP更严格的下限对应的不动点,并发现前者速度比标准BP更快。 BPNN-D在所有50个模型上收敛,而BP未能在6个模型的200次迭代内收敛。
我们记录了BPNN-D和BP使用并行更新进行收敛的迭代次数,“收敛”定义为最大因子对变量消息差为10-5。 BPNN-D的中位数改善率是BP的1.7倍,有关完整的收敛图,请参阅附录。在BP收敛的44个模型中,精确的对数划分函数和BPNN-D的估计间的RMSE为0.97,而BP为7.20。 对于44个模型中的10个模型,BPNN-D发现的不动点对应的对数分割函数下界比BP的下界大(即更好)3~22倍(对应的分割函数下界大20~e 22倍)。相反,BP发现的对数下界从未比BPNN-D发现的下界大1.7以上。
分布外泛化
……当然夸BPNN好啦
4.2随机块模型
随机块模型(SBM)是一个描述社区形成的生成模型,通常用于对社区检测算法进行基准测试[1]。
……
4.3模型计数
在本节中,我们使用BPNN来估计布尔公式的满意解的数量,这对BP很有挑战性——由于复杂的逻辑约束和0概率状态,该问题通常无法收敛。 计算满足解的确切数量(精确的模型计数)是一个#P完全问题[47]。 模型计数是许多领域中出现的一个基本问题,包括概率推理[40,9],网络可靠性[16]和检测程序中的私人信息泄漏[11]。 但是,精确模型计数的计算复杂性导致了关于近似模型计数的大量工作[46、27、28、8、20、18、24、3、5、44],目的是估算数量以较低的计算成本满足解。
训练设置
在本节中训练的所有BPNN均由5个BPNN-D层和随后的BPNN-B层组成,并经过训练以预测CNF形式的输入公式的满意解数的自然对数。 这是通过将CNF公式转换为因子图实现的,该因子图的分配/分区函数是输入公式的满意解的数量。 我们使用[44]中的基准评估了BPNN的性能,并使用DSharp [37]获得了gt模型计数。 基准分为7类,包括网络QMR问题(快速医学参考)[26],网络网格问题以及可满足性模理论库(SMTLIB)基准的位点爆破版本[12]。 每个类别包含14到105个分配给培训和验证的问题。 有关训练,数据集以及我们使用最小独立支持变量集的更多详细信息,请参见附录。
基准近似模型计数器
为进行比较,我们在所有基准上运行了两个sota近似模型计数器ApproxMC3 [12,44]和F2 [4,5]。 ApproxMC3是一种随机哈希算法,可返回模型计数的估计值,该估计值被保证以较高概率在精确模型计数的某乘法因子内。 F2放弃了概率保证以换取大大提高的计算效率。 我们还尝试使用从分类到回归的[43]架构训练GNN。 我们使用了作者的代码,对其进行了稍微的修改以进行回归,但未能成功实现non-trivial学习。
BPNN提供出色的计算效率
……
从有限的数据中学习
粗糙翻译--
我们在每个训练类别中随机抽取了70%的问题作为样本,对一个单独的BPNN进行了训练。 这使每个 BPNN仅可以学习9到73个基准。 相比之下,先前的工作通过创建 100k个示例的大型训练集,对布尔公式以析取范式(DNF)进行了近似模型计数,该模型的模型计数可以使用有效的多项式时间算法进行近似[2]。 对于基于CNF公式的模型计数,这种a不存在,因此这种方法很难处理。 尽管如此,BPNN在整个基准类别范围内都达到了与F2相当或更好的培训和验证RMSE(完整的结果请参见附录)。 这表 明BPNN可以在极度数据受限的情况下捕获SAT问题的不同系列的分布。
从简易数据到难/硬数据
粗糙翻译--
我们重复了与上一段相同的实验,但是对每个BPNN进行了DSharp解决最快的每个类别中70%的问题的训练。 对剩下的30%的问题进行了验证,而DSharp花费的时间最长。 这些严格的验证集对Dsharp而言更具挑战性。 每个类别的硬验证集中的平均运行时间是每个相应的简单训练集中的最长运行时间的4至15倍。 当对7个类别中的3个类别进行随机抽样训练和验证时,针对这些难题的验证RMSE在验证误差的33%以内。 这表明BPNN有潜力在可用数据上进行训练,然 后泛化为任何当前方法都难以解决的相关问题。 有关完整的结果,请参见附录。
跨域学习
我们对BPNN进行了随机抽样训练——随机抽样了所有类别中70%的问题,涉及网络网格问题,SMTLIB基准测试的位点爆炸版本以及网络DQMR问题。 BPNN实现了3.9的最终训练RMSE和5.31的验证RMSE,这表明BPNN能够从一个小训练集中捕获跨越多个域的广泛分布。
5 Related Work
[2]使用图神经网络执行近似加权析取范式(DNF)计数。 加权DNF计数是#P完全问题。 但是,与基于CNF公式的模型计数相比,存在用于加权DNF计数的O(nm)多项式时间近似算法(其中n是变量数,m是子句数)。 作者利用这一点生成具有近似解的100k DNF公式的大型训练数据集。
相比之下,我们的BPNN可以从少于50个问题的很小的训练数据集中学习和推广。 该结果提供了[2]结论中提到的重要的未来工作。
最近,[42]设计了一个图神经网络,该神经网络在因子图上运行并与BP交换消息以执行纠错解码。 相反,BPNN-D保留了BP的所有不动点,在树结构因子图上计算确切的分配/分区函数,并且只要从BP的不动点获得的Bethe逼近是可证明的下界,就返回下界。 所有BPNN层都将BP的对称性(不变性和等方差)保留给变量和因子索引的排列。 最终,BPNN在消息传递过程中避免了“重复计算”。
之前的工作已经表明,神经网络可以学习如何解决NP完全决策问题和优化问题[43,39,23]。[53]利用GNNs在相对较小的图形模型中进行边际推理。22]考虑改进概率编程的期望传播中的消息传递,此时用户可以指定任意代码来定义因子,不过最优更新是难以解决的。[50]考虑学习马尔科夫随机场,并解决估计边际似然的问题(一般难以精确计算)。他们使用了一个比LBP更快但计算可比估计的变换网络。这使得在训练过程中,当似然必须在每个训练步骤中计算时,可以更快地进行摊开推理。相比之下,BPNNs的性能明显优于LBP,并且可以泛化到分布外数据。
6 Conclusion
我们引入了信念传播神经网络,这是对BP的严格泛化,它学会了更快地找到更好的不动点。 BPNN架构类似于标准GNN的架构,但保留BP对变量和因子索引的排列的不变性和等方差。 我们凭经验证明,BPNNs可以从只包含10s个训练点的微小数据集中学习,并且可以泛化到与训练期间所见不同分布的测试数据中。 在准确性方面,BPNN明显优于循环式(loopy)信念传播和标准图神经网络。
BPNN提供出色的计算效率,比最新的随机哈希算法快几个数量级,同时保持相当的准确性。
Broader impact
这项工作通过对一些基准问题进行近似推断来发展sota,从而做出了理论和实践上的贡献。 另一方面,BPNN可使近似推理更具可扩展性。