【支持向量机】最大间隔超平面及Matlab代码

线性可分

在特征空间中，有两个训练样本可以通过一条直线区分开，则称为线性可分。而在特征空间大于等于四维时，分开训练样本的平面，称为超平面。

我们定义一条直线方程：${\omega }_1{x}_1+{\omega }_2{x}_2+b=0$
权重：${\omega }_1，{\omega }_2$ 偏置：$b$
$$\Rightarrow \{\begin{array}{cc}{\omega }_1{x}_1+{\omega }_2{x}_2+b>0& (i\in 1～n，y_i>1)\\ {\omega }_1{x}_1+{\omega }_2{x}_2+b<0& (i\in 1～n，y_i<1)\end{array}$$
我们规定$y$为训练样本的标签。
$$\Rightarrow \{\begin{array}{c}{y}_i=\{-1,+1\}\\ x_i=\begin{array}{c}{\left[\begin{array}{c}{x}_{i1},x_{i2}\end{array}\right]}^T\end{array}\end{array}$$
假设：
$$x={\left[\begin{array}{c}{x}_{i1}\\ x_{i2}\end{array}\right]}^T\omega ={\left[\begin{array}{c}{\omega }_{i1}\\ {\omega }_{i2}\end{array}\right]}^T$$
上述样本关系即可转化为：
$$\Rightarrow \{\begin{array}{cc}{\omega }^T{x}_i+b>0& (i\in 1～n，y_i>1)\\ {\omega }^T{x}_i+b<0& (i\in 1～n，y_i<1)\end{array}$$

我们可以得到一个严格的数学定义来判断训练样本是否线性可分:
$$y_i({\omega }^T{x}_i+b)>0$$

最大间隔

在二分类的情况下，如果一个数据集是线性可分的，即存在一个超平面将两个类别完全分开，那么一定存在无数多个超平面将这两个类别完全分开。
在机器学习中，我们不仅得关注训练误差，而且需要关注期望损失。在下图中，靠近训练样本的超平面，对噪声的影响是非常敏感的。如果噪声大于最小距离，那么分类就会出错。我们称：这个超平面的鲁棒性较差。
为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

最优化问题

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。通过上述条件可以得知，分开训练样本的最优超平面需具有三个特性：

1. 可以分开两类训练样本；
2. 平移这个超平面，使它刚好擦过特征空间中的样本点时，这些样本点称为支撑向量，且支持向量到超平面有最大化间隔（margin）；
3. 最大间隔的超平面应处于间隔中心，到所有支持向量距离相等。

任意超平面可以用下面这个线性方程来描述：
$${\omega }^{T}x+b=0$$

二维空间点$（x,y）$到直线$Ax+By+C=0$的距离公式是：
$$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$$

根据$|y_i|=1\Rightarrow y({\omega }^{T}x+b)=|{\omega }^T+b|$,拓展到n维空间后，点$x=(x_1,x_2\dots x_n)$到直线${\omega }^{T}x+b=0$的距离为：

$$\begin{gathered} d=\frac{y({\omega }^{T}x+b)}{||\omega ||} \\ =\frac{|{\omega }^{T}x+b|}{||\omega ||} \end{gathered}$$
其中
$$||\omega ||=\sqrt{{\omega }_1^2+\dots {\omega }_n^2}$$

根据：
$$s.t.:y_i({\omega }^T{x}_i+b)>0$$

$$\Rightarrow \exists \gamma >0,y_i({\omega }^T{x}_i+b)=\gamma$$
对超平面进行缩放：
$$\exists （\omega ，b）\Rightarrow （\alpha \omega ，\alpha b）$$
缩放对于超平面并无影响，规定$\gamma =1$,使$|{\omega }^{T}x+b|=1$
$$\Rightarrow \{\begin{array}{c}\frac{1}{||\omega ||}=d\\ y_i({\omega }^T{x}_i+b)=1\end{array}$$
再做一个变化：
$$max\frac{1}{||\omega ||}\iff min\frac{||\omega |{|}^2}{2}$$
所以得到最优化问题是：
$$\Rightarrow \{\begin{array}{c}min\frac{||\omega |{|}^2}{2}\\ y_i({\omega }^T{x}_i+b)>1\end{array}$$

Matlab代码

%% 线性可分数据用支持向量机分类，其求解采用二次规划函数
clc;clear;
% 初始化数据集
random_1 = unifrnd(8,12,100,2);
random = [random_1(1:50,:);random_1(51:100,:)+4];
y = [zeros(50,1)-1;ones(50,1)]; % 标签数据
X = random; % 特征数据
% 可视化
scatter(random(1:50,1),random(1:50,2),'red')
hold on
grid on
scatter(random(51:100,1),random(51:100,2),'blue')


%% 采用Matlab自带的二次规划函数求解问题
% 构建二次系数矩阵H
H = [];
for i =1:length(X)
    for j = 1:length(X)
        H(i,j) = X(i,:)*(X(j,:))'*y(i)*y(j);
    end
end
% 构造一次项系数f
f = zeros(length(X),1)-1;
A = [];b = []; % 不等式约束
Aeq = y';beq = 0; % 等式约束
ub = [];lb = zeros(length(X),1); % 自变量范围
[x,fval] = quadprog(H,f,A,b,Aeq,beq,lb,ub);
% x表示自变量的解，以及在x处的函数值
% 将很小的x直接赋值为0
x(x < 1e-5) = 0;

% 利用求解得到x求解系数w
w = [0,0];
[a,~] = find(x~=0); % 找到可以求解b的值
temp = 0;
for i = 1:length(X)
    w = w + x(i)*y(i)*X(i,:);
    temp = temp + x(i)*y(i)*X(i,:)*X(a(1),:)';
end
% 计算偏置系数
b = y(a(1)) - temp;

% 数据可视化
k = - w(1)/w(2); % 构造截距式
b_ = -b/w(2); % 构造系数b
m = 8:2:16; % 生成一些点
n = k*m+b_;
plot(m,n,'--')
n_2 = k*m+b_+1/w(2);
hold on
plot(m,n_2,'--')
n_3 = k*m+b_-1/w(2);
plot(m,n_3,'--');
grid on
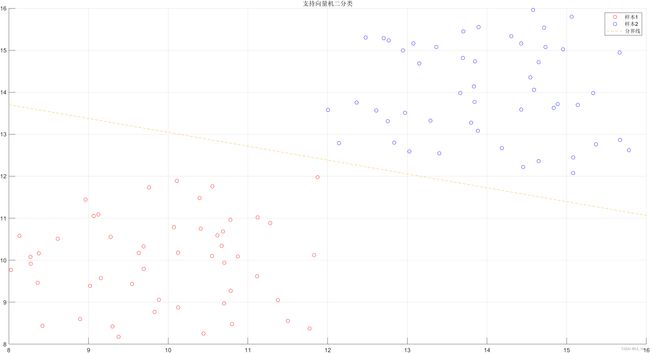
title('支持向量机二分类')
legend('样本1','样本2','分界线')

% 添加文本说明可视化
% 获取支持向量下标
Vctor_index = find(x~=0);
% 对下标进行分类
Vctor_length = length(Vctor_index); % 获取支持向量的个数
category_1 = []; % 定义第一类
category_2 = []; % 定义第二类
% 对支持向量的下标进行遍历然后一一分类
for i =1:Vctor_length
    if y(Vctor_index(i))==-1
        category_1 = [category_1;Vctor_index(i)];
    else
        category_2 = [category_2;Vctor_index(i)];
    end
end
% 分类进行可视化
%绘制第一类category_1，用红色填充
scatter(X(category_1,1),X(category_1,2),'filled','r','HandleVisibility','off')
t1 = text(X(category_1,1)+0.1,X(category_1,2)-0.1,'支持向量','Color','red');
t1.Color = 'red';

% 绘制第二类category_2，用蓝色填充
scatter(X(category_2,1),X(category_2,2),'filled','blue','HandleVisibility','off')
t2 = text(X(category_2,1)+0.1,X(category_2,2)-0.1,'支持向量','Color','blue');


% 计算支持向量到超平面的距离
D_1 = abs(w*X(category_1(1),:)'+ b)/norm(w,2);
D_2 = abs(w*X(category_2(1),:)'+ b)/norm(w,2);
disp(['正类支持向量到超平面的距离为',num2str(D_1)])
disp(['负类支持向量到超平面的距离为',num2str(D_2)])