SoftTriple Loss: Deep Metric Learning Without Triplet Sampling

1. Abstract

距离度量学习（DML）用于学习嵌入(特征提取)，其中来自同一类别的示例比来自不同类别的示例更接近。 可以将其转换为具有三元约束的优化问题。 由于存在大量三元组约束，因此DML的采样策略必不可少。随着深度学习在分类领域的巨大成功，它已被应用于DML。 当使用深度神经网络（DNN）学习嵌入时，每次迭代仅可获得一小部分数据。三重约束的集合必须在小批次中采样。 由于小批量无法很好地捕获原始集合中的邻居，因此使学习到的嵌入次优。相反，使用DNN优化作为分类损失的SoftMax损失在某些DML任务中表现出优异的性能。 它激发我们研究SoftMax的结构。我们的分析表明SoftMax损失等效于每个类别具有一个中心的平滑的triplet loss。在现实世界的数据中，一类可以包含多个局部簇，而不是一个局部簇，例如，不同姿势的鸟。 因此，我们建议使用SoftTriple损失将SoftMax损失扩展到每个类别的多个中心。与传统的深度度量学习算法相比，优化SoftTriple损失可以通过适度增加最后一个全连接层的大小来学习无需采样阶段的嵌入。在基准数据集上进行的实验证明了所提出的损失函数的有效性。Code is available at CLICK HERE

2. Introduction

距离度量学习（DML）由于其广泛的应用而在过去的几十年中得到了广泛的研究，例如k近邻分类，图像检索和聚类。使用适当的距离度量，来自同一类别的示例应该比来自不同类别的示例更接近。 已经有许多算法来学习良好的距离度量。在大多数传统DML方法中，示例都是通过手工提取的特征来表示的，而DML则是要学习一种特征映射，以将示例从原始特征空间投影到新空间。 距离可以用马氏距离计算
$${\mathrm{dist}}_M\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({\mathbf{x}}_i-{\mathbf{x}}_j\right)}^{\top }M\left({\mathbf{x}}_i-{\mathbf{x}}_j\right)$$

其中$M$是学习到的距离度量，使用这种格式，DML的主要挑战来自输入空间的维数。作为度量，学习的矩阵 $M$ 必须为半正定（PSD），而保持矩阵PSD的成本可能高达 $O(d^3)$，其中 $d$ 是原始特征的维数。早期工作直接应用PCA来缩小原始空间。后来，开发了各种策略来降低计算成本。

图1. softTriple loss 在传统的SoftMax loss中，每个类别在最后一个全连接层中都有一个中心。同一类中的示例将归纳到同一中心。如图所示，它可能不适用于现实世界的数据。相比之下，SoftTriple loss 会在全连接的层中保留多个中心（例如，在本示例中每个类别2个中心），并且每个图像都将分配给其中一个。它对于在现实数据集中的类内方差建模更为灵活。

这些方法可以从输入特征中获得良好的度量，但是手工提取的特征与任务相互独立，并且可能导致信息丢失，从而限制了DML的性能。随着深层神经网络在分类任务中的成功应用，研究人员考虑直接从深层神经网络学习嵌入。如果没有显式的特征提取，深度度量学习将极大地提高性能。在深度度量学习中，输入特征的维数不再是挑战，因为神经网络可以直接从原始数据（例如图像，文档等）中学习低维特征。相反，对于深度度量学习而言，生成用于优化的适当约束变得具有挑战性。

这是因为大多数深度神经网络都是使用随机梯度下降（SGD）算法进行训练的，并且每次迭代中只有一小部分示例可用。由于嵌入是通过锚点示例及其邻域（例如，成对约束或三重约束的有效集合）上定义的损失进行优化的，因此小批量处理中的示例可能无法很好地捕获整个邻域，尤其是对于相对较大的情况数据集。此外，小批量包含 $O(m^2)$ pairs $O(m^3)$ triplets，其中m是小批量的大小。即使对于小批量要有效地学习嵌入，有效的抽样策略也是必不可少的。有很多努力致力于研究信息丰富的小批次采样以及在小批次中对三元组采样。一些工作还试图使用proxies减少三元组的总数。对小批次和约束进行采样不仅会丢失信息而且使优化变得复杂。在这项工作中，我们考虑学习无约束采样的嵌入。

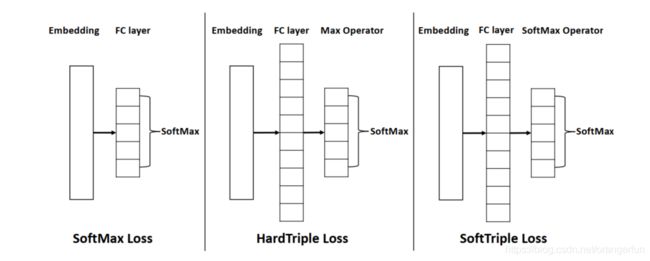
近年来的研究表明，通过优化SoftMax损失直接得到的嵌入数据在简单的基于距离的任务和人脸识别方面表现良好。这启发了我们对SoftMax loss公式的研究。我们的分析表明，SoftMax损失等同于平滑的triplet loss。通过为最后一个全连接层中的每个类别提供一个的中心，可以在原始示例, 和他相关的中心以及和他不同类的中心上定义由SoftMax损失得出的三重态约束。因此，通过优化SoftMax损失得到的嵌入可以很好地作为距离度量。然而，如图1所示，真实世界数据中的类可以由多个本地簇组成，并且单个中心不足以捕获数据的内在结构。因此，从SoftMax损失中学习到的嵌入在复杂场景中可能会失败。

在这项工作中，我们提出通过为每一类引入多个中心来改善SoftMax损失，这种新的损失被称为SoftTriple损失。与单个中心相比，多中心可以更好地捕捉数据的隐藏分布，因为它们有助于减少类内方差。这个性质对于在多中心训练时保留原始样本上的三元组约束也是至关重要的。与现有的deep-DML方法相比，SoftTriple中的三元组数与原始示例数呈线性关系。由于中心编码在最后一个全连接层中，所以SoftTriple损失可以在没有采样三元组的情况下得到优化。图1示出了所提议的SoftTriple损失。显然，SoftTriple loss必须确定每个类的中心数。为了缓解这个问题，我们开发了一个策略，在开始时为每个类设置足够多的中心，然后应用 $L_{1,2}$ 正则来获得一个紧凑的中心集。在fine-grained visual 分类任务上我们证明了所提出的损失函数，在这些任务中，捕获本地集群对于获得良好的性能至关重要。

本文的其余部分安排如下。第二部分回顾了传统的距离度量学习和深度度量学习的相关工作。第三节分析了SoftMax 损失，并提出了相应的SoftTriple loss。第4节在基准数据集上进行比较。最后，第五部分总结了本文的工作，并讨论了未来的发展方向。

2. Related Work

Distance metric learning 当输入特征被提供时，许多DML方法已经被开发出来。由于半正定矩阵投影的存在，输入特征的维数是这些方法面临的一个重要挑战，人们已经提出了许多解决方法。最直接的方法是通过PCA对输入空间进行降维。然而，PCA与任务无关，可能会影响学习嵌入的性能。一些工作试图用低秩假设来减少有效参数的数目，论文[16]通过减少PSD投影的数目来降低计算成本，论文[17]提出通过引入随机投影在低维空间中学习对偶变量，然后在原始空间中恢复度量。在解决了维度的挑战后，手工构建的特征成为性能提升的瓶颈。

在这些方法中度量学习的的约束条件形式也得到改进。早期的工作集中在优化成对约束，这要求来自同一类的示例之间的距离较小，而来自不同类的示例之间的距离较大。然后，发展了三元组约束，其中给定一个锚定示例，锚定点与相似示例之间的距离应比锚定点与不同类示例之间的距离小很多。很明显，成对约束的个数为 $O(n^2)$，而三元组约束的个数可达$O(n^3)$，其中 $n$ 是原始实例的个数。与成对约束相比，三元组约束优化了局部聚类的几何结构，更适用于类内方差的建模。本次工作中，我们将集中在三重约束上。

Deep metric learning 深度度量学习的目的是通过深度神经网络直接从原始数据（如图像）中学习嵌入。在任务相关的的embedding下，度量学习的性能有了显著的提高。然而，大多数深度模型都是用SGD训练的，在每次迭代中只允许一小批数据。由于小批量的规模很小，与原始数据相比，其中的信息是有限的。为了解决这一问题，算法必须具有有效的抽样策略来生成小批量，然后从中抽取三元组约束。一个简单的方法是增加小批量的规模。然而，大的小批量将受到GPU内存的限制，也会增加 triplet 采样的挑战。随后，论文[19]建议从相邻类生成minibatch。此外，论文[3, 12, 21, 24]提出各种各样的抽样策略来获得约束。论文[21]提出采样semi-hard负样本…然而，所有这些策略都可能无法捕捉到整个数据集的分布情况。此外，它们使得深度DML中的优化变得复杂。

Learning with proxies 近年来，一些研究者考虑减少triplet 的总数，以缓解 triplet 数量过多带来的挑战。论文[14] 用一个原始示例和两个代理构造 triplet 损失。由于代理的数量明显少于原始示例的数量，因此可以将代理保存在内存中，以帮助避免在不同批次中进行采样。但是，当标签信息可用时，它只为每个类提供一个代理，这与SoftMax类似。论文[18]提出了一种传统的DML算法，只利用潜在的例子构造三元组损失，为每个类分配多个中心，进一步减少了三元组的数目。本文提出通过SoftTriple损失来学习嵌入，从而排除采样阶段，同时捕获每个类的局部几何信息。

3. SoftTriple Loss

在这一部分中，我们首先介绍了SoftMax损失和triplet 损失，然后研究了它们之间的关系，导出了SoftTriple loss。

第$i$个样本的嵌入表示成$x_i$， 与之相应的label为$y_i$，然后深度神经网络的输出的条件概率可以使用SoftMax操作获得：

$$\mathrm{Pr}\left(Y=y_i\mid {\mathbf{x}}_i\right)=\frac{\exp \left({\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_j^C\exp \left({\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}$$

其中，$[w_1,w_2...w_c]\in R^{d\ast C}$ 是最后的全连接层， $C$ 表示类的数量， $d$是embedding的维数， 与之相关的SoftMax损失为：

$${\ell }_{\text{Soft Max }}\left({\mathbf{x}}_i\right)=-\log \frac{\exp \left({\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_j\exp \left({\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}$$

一个深层模型可以通过最小化损失来学习。这种损失已普遍应用于分类任务

给定一个三元组$(x_i,x_j,x_k)$，DML的目标是学习好的嵌入，即来自同一个类的示例比来自不同类的示例更接近，如下所示：

$$\forall i,j,k,{\Vert {\mathbf{x}}_i-{\mathbf{x}}_k\Vert }_2^2-{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }_2^2\ge \delta$$

其中 $x_i$ 和 $x_j$ 来自同一个类，$x_k$ 来自不同的类， $\delta$是预定义的一个间隔，当每个示例都有单位长度（例如：$\Vert \mathbf{x}{\Vert }_2=1$），三元组约束可以被简化成如下：

$$\forall i,j,k,{\mathbf{x}}_i^{\top }{\mathbf{x}}_j-{\mathbf{x}}_i^{\top }{\mathbf{x}}_k\ge \delta (1)$$

这里我们忽略了对 $\delta$ 的缩放。与之相应的 triplet loss 可以写成：
$${\ell }_{\text{triplet }}\left({\mathbf{x}}_i,{\mathbf{x}}_j,{\mathbf{x}}_k\right)={\left[\delta +{\mathbf{x}}_i^{\top }{\mathbf{x}}_k-{\mathbf{x}}_i^{\top }{\mathbf{x}}_j\right]}_{+}(2)$$

从等式1可以看出,总的三元组数是样本数的三次方，这使得大多数基于三元组的DML算法不可避免地要进行采样。

对于$w$和$x$的都是单位向量，归一化的SoftMax loss可以写为

$${\ell }_{{\text{SoftMax }}_{\text{norm }}}\left({\mathbf{x}}_i\right)=-\log \frac{\exp \left(\lambda {\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_j\exp \left(\lambda {\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}(3)$$

其中 $\lambda$ 是缩放因子。令人惊讶的是，我们发现用平滑项 $\lambda$ 最小化归一化SoftMax loss等同于优化平滑的triplet loss。

Proposition 1
$${\ell }_{{\text{Soft Max }}_{\text{norm }}}\left({\mathbf{x}}_i\right)=\underset{\mathbf{p}\in \Delta }{\max }\lambda \sum _j{\mathbf{p}}_j{\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)+H(\mathbf{p})(4)$$

其中 $p\in R^C$ 是类的分布，$\Delta =\left\{\mathbf{p}\mid {\sum }_j{\mathbf{p}}_j=1,\forall j,{\mathbf{p}}_j\ge 0\right\}$，$H(p)$表示分布$p$的熵

证明，根据KKT条件，等式4中的分布p有闭式解

$${\mathbf{p}}_j=\frac{\exp \left(\lambda {\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)\right)}{{\sum }_j\exp \left(\lambda {\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)\right)}$$

因此，我们有：
$$\begin{array}{l}{\ell }_{\text{Soft Max norm }}\left({\mathbf{x}}_i\right)=\lambda {\sum }_j{\mathbf{p}}_j{\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)+H(\mathbf{p})\\ =\log \left({\sum }_j\exp \left(\lambda {\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)\right)\right)=-\log \frac{\exp \left(\lambda {\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_j\exp \left(\lambda {\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}\end{array}$$

Remark 1 命题1表明，SoftMax损失优化了由一个原始例子和两个中心（如：$x_i,w_{yi},w_j$）组成的三元约束；与等式1中三元组约束条件相比，SoftMax loss 的目标是：

$$\forall i,j,{\mathbf{x}}_i^{\top }{\mathbf{w}}_{y_i}-{\mathbf{x}}_i^{\top }{\mathbf{w}}_j\ge 0$$

因此，在设计分类任务时，通过最小化SoftMax损失所得到的嵌入量可以适用于基于距离的任务。

Remark 2 没有熵正则化器，损失就变成

$$\underset{\mathbf{p}\in \Delta }{\max }\lambda \sum _j{\mathbf{p}}_j{\mathbf{x}}_i^{\top }{\mathbf{w}}_j-\lambda {\mathbf{x}}_i^{\top }{\mathbf{w}}_{y_i}$$

这相当于

$$\underset{j}{\max }\left\{{\mathbf{x}}_i^{\top }{\mathbf{w}}_j\right\}-{\mathbf{x}}_i{\mathbf{w}}_{y_i}$$

显然，它严厉的惩罚三元组且当 $x_i$ 的最近邻是与之相应的中心点$w_{yi}$时为0。熵正则化减少了离群值的影响，并使损失更加鲁棒。 $\lambda$ 在hardness of triplets 和 regularizer 之间进行权衡。此外，最小化最大熵可以使分布集中，进一步使样本远离不相关中心，这意味着样本具有较大的裕度(margin)特性。

Remark 3 使用相似分析法分析ProxyNCA损失 ：
$${\ell }_{\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{x}\mathrm{y}\mathrm{N}\mathrm{C}\mathrm{A}}\left({\mathbf{x}}_i\right)=-\log \frac{\exp \left({\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_{j\ne y_i}\exp \left({\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}$$

我们有：

$${\ell }_{\text{ProxyNCA }}\left({\mathbf{x}}_i\right)=\underset{\mathbf{p}\in \Delta }{\max }\lambda \sum _{j\ne y_i}{\mathbf{p}}_j{\mathbf{x}}_i^{\top }\left({\mathbf{w}}_j-{\mathbf{w}}_{y_i}\right)+H(\mathbf{p})$$

其中 $p\in R^{C-1}$ ，与SoftMax损失相比，它去除了只包含相应类中心的基准三元组，使得损失无界。我们的分析表明，损失可以有界，如等式2所示：${\ell }_{\text{Proxy NCA }}^{\text{hinge }}\left({\mathbf{x}}_i\right)={\left[-\log \frac{\exp \left({\mathbf{w}}_{y_i}^{\top }{\mathbf{x}}_i\right)}{{\sum }_{j\ne y_i}\exp \left({\mathbf{w}}_j^{\top }{\mathbf{x}}_i\right)}\right]}_{+}$。验证有界损失不在这项工作的范围之内。

尽管优化SoftMax loss可以学习有意义的特征嵌入，但缺点很简单。它假设每个类只有一个中心，而现实世界中由于类内的巨大差异而可能包含多个局部簇，如图1所示。传统的SoftMax损失产生的三元组约束过于简单，无法捕捉原始数据的复杂几何结构。因此，我们为每个类引入多个中心。

3.1 Multiple Centers

现在，我们假设每个类都有 $K$个中心。然后，可以将示例$x_i$与类别 $C$之间的相似性定义为:

$${\mathcal{S}}_{i,c}=\underset{k}{\max }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k(5)$$

注意，相似性的其他定义也可以适用于这个场景（例如：${\min }_{\mathbf{z}\in {\mathbb{R}}^K}{\Vert \left[{\mathbf{w}}_c^1,\cdots ,{\mathbf{w}}_c^K\right]\mathbf{z}-{\mathbf{x}}_i\Vert }_2$）我们用一个简单的形式来说明多中心的影响。

通过定义相似性，三元组约束要求一个示例比其他类更接近其对应的类

$$\forall j,{\mathcal{S}}_{i,y_i}-{\mathcal{S}}_{i,j}\ge 0$$

如前所述，最小化熵$H(p)$有助于将示例拉到相应的中心。为了明确地打破这种联系，我们考虑引入像等式1中传统三元组损失中的小间隔，并将约束定义成如下形式：

$$\forall j_{j\ne y_i},{\mathcal{S}}_{i,y_i}-{\mathcal{S}}_{i,j}\ge \delta$$

通过替换等式4中的相似性，我们可以得到HardTriple loss 如下：

$$\begin{array}{l}{\ell }_{\text{HardTriple }}\left({\mathbf{x}}_i\right)={\max }_{\mathbf{p}\in \Delta }\lambda ({\sum }_{j\ne y_i}{\mathbf{p}}_j\left({\mathcal{S}}_{i,j}-\left({\mathcal{S}}_{i,y_i}-\delta \right)\right)+{\mathbf{p}}_{y_i}\left({\mathcal{S}}_{i,y_i}-\delta -\left({\mathcal{S}}_{i,y_i}-\delta \right)\right))+H(\mathbf{p})\\ =-\log \frac{\exp \left(\lambda \left({\mathcal{S}}_{i,y_i}-\delta \right)\right)}{\exp \left(\lambda \left({\mathcal{S}}_{i,y_i}-\delta \right)\right)+{\sum }_{j\ne y_i}\exp \left(\lambda {\mathcal{S}}_{i,j}\right)}(6)\end{array}$$

HardTriple损失通过为每个类提供多个中心来改善SoftMax损失。 但是，它需要通过max运算在每个类别中获取最近的中心，而该运算并不平滑，并且分配在多个中心之间可能很敏感。 受SoftMax损失的启发，我们可以通过平滑max运算符来提高鲁棒性。

考虑如下问题：

$$\underset{k}{\max }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k$$

它相当于

$$\underset{\mathbf{q}\in \Delta }{\max }\sum _k{\mathbf{q}}_k{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k(7)$$

我们把熵正则化器加到分布q上，如下所示：

$$\underset{\mathbf{q}\in \Delta }{\max }\sum _k{\mathbf{q}}_k{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k+\gamma H(\mathbf{q})$$

通过与命题1类似的分析，q的闭式解为：

$${\mathbf{q}}_k=\frac{\exp \left(\frac{1}{\gamma }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k\right)}{{\sum }_k\exp \left(\frac{1}{\gamma }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k\right)}$$

把它带回等式7中，我们定义了示例 $x_i$ 和类 $C$之间的松弛相似性如下：

$${\mathcal{S}}_{i,c}^{\prime }=\sum _k\frac{\exp \left(\frac{1}{\gamma }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k\right)}{{\sum }_k\exp \left(\frac{1}{\gamma }{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k\right)}{\mathbf{x}}_i^{\top }{\mathbf{w}}_c^k$$

通过应用平滑的相似度，我们将SoftTriple损失定义为：

$$\begin{array}{rlr}& {\ell }_{\text{SoftTriple }}\left({\mathbf{x}}_i\right)& =-\log \frac{\exp \left(\lambda \left({\mathcal{S}}_{i,y_i}^{\prime }-\delta \right)\right)}{\exp \left(\lambda \left({\mathcal{S}}_{i,y_i}^{\prime }-\delta \right)\right)+{\sum }_{j\ne y_i}\exp \left(\lambda {\mathcal{S}}_{i,j}^{\prime }\right)}\end{array}$$

图2说明了SoftMax损失和我们所提出的损失之间的差异；最后，我们将证明应用中心构造三元组约束的策略可以恢复原始三元组的约束。

图2. SoftMax损失与我们提出的损失之间的差异说明 与SoftMax损耗相比，我们首先增加FC层的尺寸，以便每个类别包括多个中心（例如，在此示例中每个类别2个中心）。 然后，我们通过不同的运算获得每个类的相似性。 最后，利用从每个类别获得的相似性来计算不同类别的分布。

定理1. 给定两个样本 $x_i$ 和 $x_j$， 他们来自同一个类别且有相同的最近中心。$x_k$来自不同的类别，如果包含中心的三元组常数满足：${\mathbf{x}}_i^{\top }{\mathbf{w}}_{y_i}-{\mathbf{x}}_i^{\top }{\mathbf{w}}_{y_k}\ge \delta$，且我们假设 $\forall i,{\Vert {\mathbf{x}}_i-{\mathbf{w}}_{y_i}\Vert }_2\le ϵ$，那么可以得到：
$${\mathbf{x}}_i^{\top }{\mathbf{x}}_j-{\mathbf{x}}_i^{\top }{\mathbf{x}}_k\ge \delta -2ϵ$$

证明：

$$\begin{array}{l}{\mathbf{x}}_i^{\top }{\mathbf{x}}_j-{\mathbf{x}}_i^{\top }{\mathbf{x}}_k={\mathbf{x}}_i^{\top }\left({\mathbf{x}}_j-{\mathbf{w}}_{y_i}\right)+{\mathbf{x}}_i^{\top }{\mathbf{w}}_{y_i}-{\mathbf{x}}_i^{\top }{\mathbf{x}}_k\\ \ge {\mathbf{x}}_i^{\top }\left({\mathbf{x}}_j-{\mathbf{w}}_{y_i}\right)+{\mathbf{x}}_i^{\top }\left({\mathbf{w}}_{y_k}-{\mathbf{x}}_k\right)+\delta \\ \ge \delta -{\Vert {\mathbf{x}}_i\Vert }_2{\Vert {\mathbf{x}}_j-{\mathbf{w}}_{y_i}\Vert }_2-{\Vert {\mathbf{x}}_i\Vert }_2{\Vert {\mathbf{w}}_{y_k}-{\mathbf{x}}_k\Vert }_2\\ =\delta -{\Vert {\mathbf{x}}_j-{\mathbf{w}}_{y_i}\Vert }_2-{\Vert {\mathbf{w}}_{y_k}-{\mathbf{x}}_k\Vert }_2\ge \delta -2ϵ\end{array}$$

定理1证明了在原三元组约束条件下，优化由中心组成的带间隔 $\delta$ 的三元组可以保留大间隔特性。这也意味着更多的中心可能有助于减少类内差异 $ϵ$。极端情况下，中心的数量等于样本的数量，此时 $ϵ$ 变为0。但是，添加更多的中心将增加最后一个完全连接的层的大小，并使优化速度变慢，并且计算量很大。此外，它可能会导致过度拟合的问题。因此，我们必须为每个类选择一个适当的中心数，这样在保持一个紧凑的中心集的同时，可以有一个小的近似误差。我们将在下一小节中演示该策略。

3.2 自适应中心数

为数据找到适当数量的中心是一个具有挑战性的问题，这也出现在无监督学习中，例如聚类。中心数K在效率和有效性之间进行权衡。在常规DML算法中，K等于原始样例数。它使三元组约束的总数达到原始实例数的三次方。在SoftMax损失中，K = 1将约束的数量减少到线性级，这效率很好，准确率不行。如果不事先知道每个类的分布，很难精确地设置K。与为每个类设置适当K的策略不同，我们建议设置足够大的K，然后鼓励相似的中心彼此合并。它可以保持生成中心的多样性，同时减少唯一中心的数目

对于每个中心 $w_{tj}$，我们可以生成一个矩阵

$$M_j^t={\left[{\mathbf{w}}_j^1-{\mathbf{w}}_j^t,\cdots ,{\mathbf{w}}_j^K-{\mathbf{w}}_j^t\right]}^{\top }$$

如果 $w_j^s$ 和 $w_j^t$ 是相似的，他们可以合并成相同的一个例如：${\Vert {\mathbf{w}}_j^s-{\mathbf{w}}_j^t\Vert }_2=0$，这是矩阵 $M_j^t$ 的第$s$行的 $L_2$正则。因此，我们对矩阵 $M_j^t$中的行进行$L_2$正则来获取稀疏的中心集，这可以被写成 $L_{2,1}$正则

$${\Vert M_j^t\Vert }_{2,1}=\sum _s^K{\Vert {\mathbf{w}}_j^s-{\mathbf{w}}_j^t\Vert }_2$$

通过在多个中心上累积$L_{2;1}$范数，我们可以将第 $j$ 类的正则化为:

$$R\left({\mathbf{w}}_j^1,\cdots ,{\mathbf{w}}_j^K\right)=\sum _t^K{\Vert M_j^t\Vert }_{2,1}$$

因为 $w$ 是单位向量，正则化可以简写成：

$$R\left({\mathbf{w}}_j^1,\cdots ,{\mathbf{w}}_j^K\right)=\sum _{t=1}^K\sum _{s=t+1}^K\sqrt{2-2{\mathbf{w}}_j^{s\top }{\mathbf{w}}_j^t}$$

使用正则化器，我们的最终目标是:

$$\min \frac{1}{N}\sum _i{\ell }_{\text{Soft Triple }}\left({\mathbf{x}}_i\right)+\frac{\tau {\sum }_j^{C}R\left({\mathbf{w}}_j^1,\cdots ,{\mathbf{w}}_j^K\right)}{CK(K-1)}$$

其中 N 是样本总数

4. Experiments

我们在三个基准的视觉分类数据集上进行了实验：CUB-2011, Cars196 和 SOP。为了公平比较，我们按照其他实验进行了参数设置。尤其是我们使用了带有BN的Inception网络作为主要结构。预训练网络使用了在ImageNET ILSVRC2012 数据集训练的参数初始化，然后在目标数据上进行fine-tune。图片被裁剪成 224*224大小作为输入。在训练过程中，只使用随机水平镜像和随机裁剪作为数据增强。模型由Adam优化，批量大小为32个，迭代次数为50个。主干网和中心的初始学习率分别设置为1e-4和1e-2。然后，在20到40个迭代次数时，他们会被处以10。考虑到CUB-2011和Cars196中的图像与ImageNet中的图像相似，我们在这两个数据集上将BN冻结，并在另一个数据集上进行BN训练。实例和中心的嵌入在实验中具有单位长度。

我们将所提出的的triplet loss和normalized SoftMax loss进行了比较。softMax loss 见等式3，softTriple 见等式10。在softTriple中我们设置 $\tau =0.2$， $\gamma =0.1$。除此之外，我们设置小间隔 $\delta =0.01$ ，中心的数量 $K=10$

我们在检索和聚类任务上使用不同方法评估了所学习到的embedding的性能。对于检索任务，我们使用了 Recall@K指标，聚类的效果使用NMI指标。

4.1 CUB-2011

首先，我们在细粒度鸟类数据集CUB-2011比较了方法，它由200种鸟类，11788张图像组成。按照通常的做法，我们将数据集拆分为前100个类用于训练，其余用于测试。我们注意到，不同的研究反馈了不同尺寸的embedding，而嵌入尺寸对性能有显著影响。为了公平起见，我们使用了64维度的embedding，该维度是许多现存方法所采用的，我们还使用了512维的特征embedding，该维度在很多数据集上达到了最好的结果。

表1 总结了64维度embedding的结果

4.2 Cars196